1. 引言
随着风力发电技术的迅速发展以及对其研究的不断深入,风电并网容量在电网中的比例也越来越大,因此对电力系统带来的影响也越来越大,对电力系统稳定性、经济运行、安全调度、调频调峰等带来很大挑战,电网互联规模不断增大,使系统的结构随之更加复杂,系统内部的电气联系更加薄弱,从而导致电力系统低频振荡现象频发。一个回路的振荡可能是其他回路的扰动引起,因此分析振荡的传播路径并准确定位故障源对消除振荡影响很有帮助。检测到一个或多个振荡的存在非周期性扰动以及过程失调中找到各种扰动的最可能根源,准确判断扰动源位置对抑制由强迫振荡引发的电网低频振荡具有重要意义。
国内外有不少学者对低频振荡作用机理和不同环境下电力系统低频振荡影响研究。文献 [1] 从电力系统模型出发,利用特征值分析法研究系统的振荡模式,通过计算参与因子的数值研究系统状态变量,揭示了简单风力发电系统产生低频振荡的机理,系统性比较研究风机类型、并网位置和风电接纳方式3个因素对系统振荡模式和阻尼特性的影响。文献 [2] 提出了一种调速系统引发低频振荡的机理识别方法,基于WAMS的振荡特征提取和系统初步模态分析,形成低频振荡产生机理的判据,判断振荡产生机理是负阻尼振荡还是强迫振荡。文献 [3] 提出了一种基于广域相量测量单元(PMU)和人工神经网络(ANN)的方法来实时预测系统振荡状态。商显俊 [4] 基于一种能量函数的构造形式,通过数学推导将其分解为状态能量、往复振荡能量和耗散能量3部分,耗散能量的流向显示了扰动能量的来源和去向,可据此识别扰动源的具体位置并提出扰动源的在线搜索策略。杨婷 [5] 利用发电机有备用容量的频率响应评估模型,结合算例进一步分析影响电力系统频率响应因素。邢光正,吴琛,陈磊,黄伟,程旻团队 [6] 基于VSC接入无穷大系统的详细模型,针对不同控制模式,系统地总结了VSC小扰动失稳的不同机理。文献 [7] 建立用于含直驱风电场的交直流混合系统小干扰稳定分析的微分方程模型在4种不同运行接线方式下的小信号稳定性计算结果。文献 [8] 以安全域方法为基础,分析输电距离、双馈风机有功控制回路与无功控制回路PI参数对系统低频振荡稳定性的影响。文献 [9] 针对振荡扰动源识别及定位,建立了单机无穷大电力系统模型,在总结负阻尼低频振荡机理的基础上,分析了强迫功率振荡的基本原理。
在研究低频振荡作用机理后,不少学者也提出关于低频振荡定位方法。文献 [10] 提出基于模态和测量数据的主要分析方法,从PMU数据中获得了母线振荡频率和电压幅值的基本特性,提出了低频振荡抑制措施。安成团队 [11] 对超低频频率振荡从改善机组阻尼、改善系统阻尼和调整系统结构3个方面,研究未来切换型超低频频率振荡抑制方向。陈骁 [12] 在各元件线性化模型的基础上,建立了以风机或锁相环的反馈子系统,研究了双馈风机与电力系统动态交互对系统低频振荡模式的影响。文献 [13] 通过在控制系统中附加阻尼控制器的方法,运用数学推导和仿真分析,证明其可以有效抑制系统低频振荡。文献 [14] 建立了含储能的单机无穷大系统线性化数学模型,利用阻尼转矩分析法和特征值分析法,分析储能装置抑制系统低频振荡的作用机理。郑凯元、杜文娟、王海风团队 [15] 利用三次Hermite插值函数提取各个测点的低频振荡扰动变量,然后通过比较各个测点扰动电压的幅值大小定位低频振荡源机组。
然而,如果想要对振荡源进一步准确定位,对于数据的选用需要更加庞大的数据量,但是上述文献在面对大量数据运算,会出现计算时间过长,计算不准确等问题。本文利用功率谱的相关性分析,结合过程知识来定位振荡源并且分析振荡的传播路径,将Prony方法与PMU数据进行拟合,利用主元分析对功率谱矩阵的降维处理从而达到减少计算量,获得准确计算结果,最后给出低频振荡检测结果。
2. 基本理论
2.1. Prony算法 [5]
该算法用指数函数线性组合拟合信号样本,假设有N个原始数据x(n),
,可以建立一个指数模型:
(1)
(2)
(3)
其中
是幅值,
是相位,
是衰减因子,
是振荡频率,是采样间隔。为使构建的模型和真实模型的误差最小,我们利用最小二乘法则构造一个目标函数:
(4)
根据式(4)我们可以得出频率、幅值、相位和衰减因子,这个方程我们可以通过求解非线性的最小二乘问题可以解决。
(5)
(6)
(7)
(8)
2.2. Prony算法中的参数选择
Prony算法拟合的结果及精确程度和其参数的选择有紧密的联系,参数选择不当就可能导致Prony算法很有可能无法进行拟合。Prony算法主要参数及和其选择基本标准遵循以下规律。
采样频率:根据信号的采样原则,为了避免采样中的频率混叠问题,我们要尽量使采样的频率大于原始信号的最高频率的2倍。由于在实际应用中,采样频率还应有较大的裕度,所以刚刚大于最高频率两倍还不够,最好是4~5倍。由于我们只对低频振荡进行研究,所以我们只需要关注频率段在0.1~2.5 Hz。
模型阶数n:电力系统处于动态过程中时,系统实际的阶数是非常高的,所以我们求得的拟合模型是一个相对实际模型降阶了的模型。而通常这个模型的阶数是未知的。Prony方法可以用以下方法确定阶数:先初选阶数L,对一组数据进行初次的Prony分析,其中,L应该大于信号中实际包含的指数项个数,然后得到L个指数项分量。再从L个分量中,选取n个分量的最优子集,再让n个指数项分量的最小平方数能够在意义上逼近我们观察到的数据。另外,Hocking和Leslie也提出过一种方法,在这种方法中,最优子集无需去搜索所有n个分量的组合,只需要按照每个指数项分量对平方差的影响程度进行排序,从n为1开始,取出对误差平方和影响程度最大的一项,再增大n,一直到误差平方和的减小速率开始显著降低为止。这个时候的n就可以作为Prony分析中使用的模型阶数。
2.3. 主元法
对振荡进行定位首先需要可靠的振荡检测方法,时域的检测方法通常利用绝对偏差积分,频域的方法可以借助功率谱或者小波分析,此外还有自相关方程ACF以及ARMA模型。根据维纳一辛钦定理,宽平稳随机过程的功率谱密度与其自相关函数是一对傅立叶变换对。对于离散随机过程x(n),归一为零均值单位方差后为
,其自相关函数为式(9)所示,则其功率谱密度可通过式(10)完成。
(9)
(10)
由相同原因引起的振荡在振荡周期上比较接近,离振荡源更近的信号受故障的影响更严重更直接,和振荡源的相似性也越高。用频域分析各回路过程输出过程的相似程度,也可以消除时滞的影响。比较2个信号的功率谱的相似性,可以通过计算欧式距离,欧式夹角等方法,对于回路中数据较大来说,计算任意个信号的欧式夹角的计算量是比较大的,这里采用了主元分析来辅助减少计算量。对m个信号的功率谱组成的矩阵进行主元分解,找到一组新的基
,以及降序排列的得分向量
,选择能代表原信号一定变化信息如数目最少的得分向量p个式,则原来的第i个信号的功率谱可以用式(6)来近似,其中ti为T的第i行,wj为w的第j列。xi在新的基
组成的空间中的近似映射为其相应的得分向量
,在新的空间中,各得分向量相似性可以代表相应的xi在原基空间中相似性。在原空间中,计算M个变量任2个长度为的向量的欧氏距离的算法复杂度为
,而主元提取通常可以将上万的数据降维到个10主元左右,计算量减小了
倍
(11)
(12)
(13)
2.4. 基于改进的Prony主元方法
对于单机无穷大系统,发电机采用二阶经典模型,在小扰动情况下线性化转子运动方程为:
(14)
式中M为机组的惯性常数;D为发电机阻尼系数;
为扰动功率变化量;
为电功率变化量;
为转子角偏移;
为转速变化量;
,
为基准频率。对式子(14)进行初积分,可得系统的能量函数为:
(15)
即
(16)
式中:VKE为动能函数;VPE为势能函数;VM为外施扰动能量函数;VD为阻尼耗散能量函数。在强迫振荡稳态阶段,扰动频率与系统固有频率近似相等,此时外施扰动做功与系统阻尼耗散的能量相等(
),系统的动能与势能完全转换(
),系统表现为无阻尼自由振荡,这是共振情况下的能量转换。
在强迫振荡的稳态阶段,各状态量都以扰动频率周期性变化,设
(17)
(18)
其中
和
分别为支路功率和频率的变化幅度;
和
分别为支路功率和频率变化的初相位;
为扰动频率。代入式(18)可得;
(19)
令
(20)
(21)
(22)
我们可以看到势能函数是由一条幅值为a,周期为
初相角为
的正弦曲线和一条斜率为b的直线叠加而成。由外施扰动注入系统并在网络中传播消耗的能量主要由非周期分量体现。定义势能流出节点为正、流入节点为负。由于c为不随时间变化的初始常数,因此,通过斜率b即可判断支路势能的方向,当b > 0时势能趋势为流出节点,当b < 0时势能趋势为流入节点。根据式(21),由于b的正负主要由
决定,因此振荡主导模式下电功率和频率变化量的初相位差决定了势能的流动方向;而b的大小还与
和
有关,通过对这些参数的辨识即可判断出支路势能的大小,并进而确定扰动源可能存在的位置。本文定义b为“能流方向因子”。
2.5. 流程图分析
图1为本文提出的Prony结合主元法流程图,Prony结合主元法电力系统振荡局部特性分析方法包含以下步骤:
1) 步骤1大量电力系统PMU数据,通过Prony构造指数模型建立函数,获得频率、相角等相关信息。
2) 步骤2电力系统频率进行计算自相关函数ACF和功率谱密度S(f)。
3) 步骤3主元法对数据进行降维处理,计算任意两个数据间欧式距离,反映其功率谱相似性。
步骤4能流因子d功率谱的相似性,决定势能的流动方向,通过对这些参数的辨识判断出支路势能的大小,进而确定扰动源可能存在的位置。
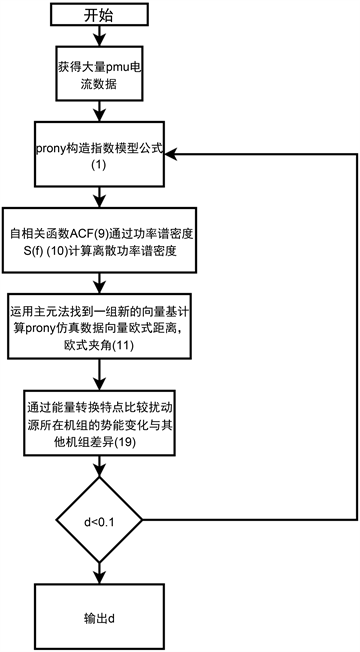
Figure 1. Flowchart of Prony combined with principal element method
图1. Prony结合主元法流程图
3. 算例仿真
3.1. Prony参数选择
我们采取一组电力系统中PMU电流数据,并运用Prony算法对大量的电流数据进行拟合,完成数据分析和绘图后得到拟合电流数据。关于采样数据进行的Prony分析,模型阶数的选择很重要,对分析结果有较大影响。如图2所示通过选10阶模型的分析结果Prony拟合波形和原图形还有一定的误差,且目标函数的误差很大,最大达到了6000。电力系统动态过程中系统阶数非常高,通常情况下,模型的阶数是未知的。所以要严格按照Prony方法常用的定阶方法选取合适的模型阶数。如图3所示我们增大模型阶数到100阶,通过实验可以发现,拟合波形明显更加精确,目标函数的误差(用方差表示)也降低到了30以下。
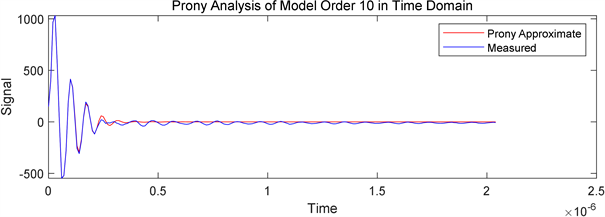

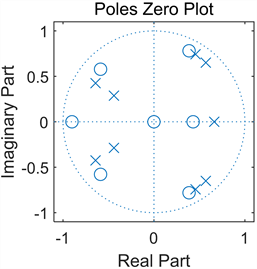
Figure 2. Prony analysis results when the sample data are 400 groups and the model order is 10
图2. 采样数据为400组,模型阶数为10时的Prony分析结果
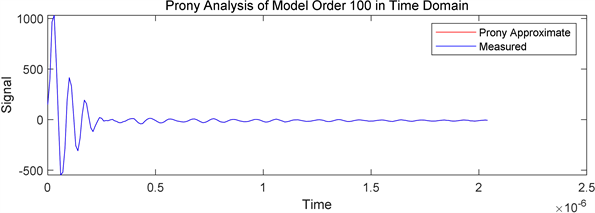

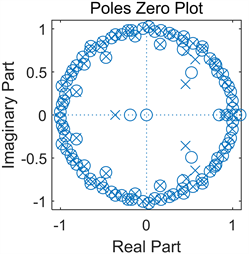
Figure 3. Prony analysis results when the sample data are 400 groups and the model order is 100
图3. 采样数据为400组,模型阶数为100时的Prony分析结果
通过以上分析可知,要想获得更加精确的拟合结果,我们应该提高模型阶数,在实验中将模型阶数提高到150阶,通过图4分析模型拟合精度已经达到很好的效果。



Figure 4. Prony analysis results when the sample data are 400 groups and the model order is 150
图4. 采样数据为400组,模型阶数为150时的Prony分析结果
3.2. Prony结合振荡源定位分析
通过低频滤波后得到ACF进行分析,将拟合完成的大量PMU数据通过计算数据间欧式夹角分析其相似程度,由相同原因引起的振荡在振荡周期上比较接近,离振荡源更近的信号受故障的影响更严重更直接,和振荡源的相似性也越高,通过双相干法和相关性分析方法等非线性分析方法,辅助故障诊断和振荡源定位工作。在计算大量PMU时,计算任意2个信号的欧式夹角的计算量是比较大的,本文采用了主元分析来辅助减少计算量,如表1所示的数据,通过运用PCA将大量的PMU电流数据一步步提取主元进行不断迭代,获得可以代表PMU数据的主元,通过计算主元部分的得分向量之后进行计算欧式夹角,欧式距离通过振荡源相似性分析,由图5圆形直观图可以看出在运用降维后对振荡源不断进行逼近,相较于最外侧未加主元法的算法获得了更高的精度从而进行振荡源定位。
3.3. Prony定位振荡源分析
表1中数据为普通算法振荡源定位数据与加主元法迭代振荡源数据,从图5直观图中可以看出d = 1.033 m是功率谱振荡相似性最高的位置,由此可以判断振荡源在(0, 1.0482 m)这个范围中。

Table 1. Principal element method iterative oscillation source position data table
表1. 主元法迭代振荡源位置数据表
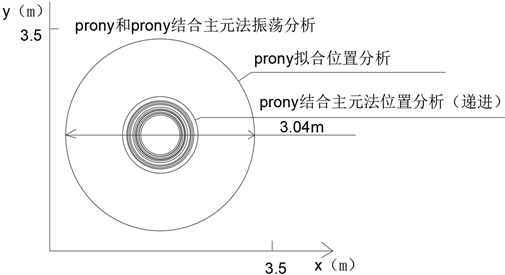
Figure 5. Prony analysis results when the sample data are 400 groups and the model order is 150
图5. 采样数据为400组,模型阶数为150时的Prony分析结果
4. 结论
随着能源互联网的提出,将风电并入互联大电网中具有更加重要的意义。风电的优势是清洁、可再生、储量丰富、技术较为成熟,近年来得到了迅速发展。风力发电的容量和规模都在不断增大。但是由于风能不稳定的特性,风电大规模并网出现了一些问题,影响到了电网的安全稳定运行,所以研究风电并网的影响具有重大意义。本文主要工作和结论总结如下:
1) 归纳和分析了不同区域互联电力系统低频振荡的产生机理,并且基于模态和测量数据归纳了一些主要分析方法及低频振荡抑制措施;从理论上进行风电场接入多机互联电网的低频振荡的影响分析。当风电场与电网之间距离、风电场出力等因素变化时,系统总阻尼增量将发生变化,系统阻尼特性发生改变。后面为了验证这一结论是否正确,将对风速、风电场出力和风电并网输送距离等因素来进行仿真分析。
2) 分析介绍了MATLAB中Prony工具箱在电力系统低频振荡的模态辨识中的作用,详细分析了在不同采样数据和模型阶数下对数据的拟合程度。找到了在兼顾效率的同时拟合数据精度最佳的采样数据和模型阶数。
3) 由于实际系统中存在噪声和面对数据量过于庞大问题,导致扰动源定位不准确、不高效,针对这一问题,本文提出了运用主元法对拟合PMU电流数据振荡分量提取与分析方法。通过采用PCA降维,对拟合完成的大量PMU电流数据进行简化,对电力系统低频振荡扰动源定位更加快捷准确,能够适应电网在线计算的要求。
4) 针对风电并网对电力系统低频振荡影响的问题,本文通过分析系统低频振荡中振荡能量组成及变化,针对传统能量函数的强迫扰动源定位不适用于系统详细的数学模型和准确的模型参数未知的情况这一问题,提出采用Prony结合能量函数通过功率谱相似性分析定位系统振荡源,运用Prony分析方法用一组指数函数的线性组合来拟合等间距采样信号,幅值、衰减、频率、相角,获得能量函数需要的数据信息。通过仿真某二线城市电网PMU数据,验证了该方法的确定性,距离扰动源越近功率谱相似性越高,最终对振荡源进行定位。
5) 本文选用了典型的两区域系统进行仿真研究,但是该系统规模不大,与实际系统的近似度有待提高,可以在此基础上,建立更加复杂的电力系统模型,更进一步研究风电并网对系统低频振荡特性的影响,使研究结果更适用于实际大规模互联电力系统。
本文中仅用非线性分析对于进一步找到振荡源还有局限性,如何进行更加准确的扰动源定位,有待进一步研究。
基金项目
清华大学电力系统及大型发电设备安全控制与仿真国家重点实验室基金资助项目(SKLD20M17);北京市高等教育学会项目(YB2021131);中国建设教育协会教育教学科研课题项目(2021051);北京建筑大学金字塔人才培养工程项目(JDYC20200324);北京建筑大学研究生教育教学质量提升项目(J2022007);北京建筑大学社会实践与创新创业课程项目(SJSC1913);北京建筑大学研究生创新项目(PG2022132);国家级大学生创新创业训练计划项目(202110016052, S202110016122, S202110016123, X202110016177, X202110016178, X202110016179);国家自然科学基金委青年科学基金资助项目(51407201)。