基于ARIMA模型的重庆GDP预测研究

Research on Chongqing GDP Forecast Based on ARIMA Model

摘要: 对1978年至2021年重庆GDP数据，利用R软体建立ARIMA模型，对建立的模型进行优化评估，并用该模型预测重庆2017~2021年GDP数据，与真实数据进行比较，以确定模型预测的准确性。根据建立的时间序列分析得到最优模型为ARIMA(2, 2, 2)，预测值与实际值的平均相对误差为1.36%，ARIMA模型很好地拟合了重庆GDP发展的趋势。可以利用ARIMA模型进行较准确的短期预测，为重庆经济的发展提供参考。

Abstract: Based on the GDP data of Chongqing from 1978 to 2021, the ARIMA model was established by R software, and the model was optimized and evaluated. The model was used to predict the GDP data of Chongqing from 2017 to 2021, and compared with the real data to determine the accuracy of the model prediction. According to the established time series analysis, the optimal model is ARIMA(2, 2, 2), and the average relate error between the predicted value and the actual value is 1.36%. The ARIMA model fits the GDP development trend of Chongqing well. The ARIMA model can be used to make a more accurate short-term forecast and provide reference for the economic development of Chongqing.

1. 引言

GDP (国内生产总值)，是一个国家(或地区)所有常住单位在一定时期内生产活动的最终成果。GDP是国民经济核算的核心指标，也是衡量一个国家或地区经济状况和发展水平的重要指标。重庆是国家中心城市，是西部大开发的重要战略支点、处在“一带一路”与长江经济带的联结点上，还有成渝地区双城经济圈、西部陆海新通道等国家战略部署“加持”，区位优势明显、战略意义重大。由此可见，重庆重要的政治地位和地理位置对西部经济的发展起到了很重要的作用。最近几年来，重庆的经济呈现快速增长的趋势，曾连续15年保持两位数高增长，自2018年开始，GDP增速放缓。本文就对重庆GDP数据进行分析研究，而预测重庆GDP具有一定的现实和指导意义。

差分自回归移动平均(differential autoregressive moving average, ARIMA)模型是由美国统计学家Box和英国统计学家Jenkins于20世纪70年代初提出的时间序列分析、预测和控制的方法，又称Box-Jenkins法，主要用于拟合具有平稳性或者可以被转换为平稳序列的时间序列。

ARMA(p, q)模型是自回归模型(AR)和滑动平均模型(MA)的结合形式，方程形式为：

$r_t={\varphi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\varphi }_i{r}_{t-i}}+a_t-{\displaystyle \underset{i=1}{\overset{q}{\sum }}{\theta }_i{a}_{t-i}}$

$\left\{a_t\right\}$ 是白噪声序列，p、q是非负整数，The AR and MA models是ARMA(p, q)模型的特例。使用滞后算子运算，模型也可以表示为：

$\left(1-{\varphi }_{1}B-\cdots -{\varphi }_p{B}^p\right)r_t={\varphi }_0+\left(1-{\theta }_{1}B-\cdots -{\theta }_q{B}^q\right)a_t$

ARMA模型只能在的平稳时间序列中应用，对于非平稳的序列，ARMA模型却不再适用，这时就需要引入一个新的模型ARIMA，即对所要研究的非平稳时间序列做差分(differencing)，ARIMA(p, 1, q)意味着非平稳时间序列做一次差分达到平稳，ARIMA(p, 2, q)意味着非平稳时间序列做二次差分达到平稳后可建模 [1]。

2. 模型的资料和方法

本文的重庆GDP数据来自于中国统计年鉴，1978~2021的GDP数据。

首先对所要建模的重庆GDP数据进行平稳性检验，即单位根检验。使用urca程序包中ur.df函数进行检验式的判断与单位根的检验 [1]。5%的显著性水平下无法拒绝原假设，认为存在单位根，GDP时间序列是非平稳的，进行第一次差分。对差分后的GDP再进行单位根检验，发现5%的显著性水平下仍然无法拒绝原假设，认为存在单位根，一阶差分后的GDP时间序列是非平稳的。二次差分后的GDP单位根检验，在5%的显著性水平下拒绝原假设，认为不存在单位根，二阶差分GDP时间序列是平稳的，故所建模型应为ARIMA(p, 2, q)。

用TSA程序包的EACF来计算样本的EACF值，估计可能的p、q值。从样本EACF图可以看到一个明显的倒三角区域，其左上方断点在AR = 1与MR = 2处，再结合ACF图与PACF图所看到的图形形态，试着选择多个p、q，用AIC最小的准则，选取最佳模型 [1]。

用ACF图和Ljung-box统计量检验残差是否符合白噪声，以确定模型是否合适与充分。

用拟合值(原始序列值 + 残差)的算法，将所有观察值的拟合值算出，并跟原始数列比较来检验模型的可靠性 [2]。

利用所建模型，预测2017~2021年的重庆GDP分析可看到来检验模型的预测性能。

3. ARIMA模型对重庆GDP的预测及实证结果分析

对重庆1978~2021年44个GDP数据进行分析，为了检验模型的预测能力，现在选取前39个GDP数据即1978~2016的用来建模，利用所建模型预测后5年(2017~2021)的GDP与实际值进行比较来检验模型的预测能力。

利用FinTS包中的FinTS.stats函数得到重庆GDP数据(1978~2021)的常用描述性统计量如下表1：

Table 1. Descriptive statistics for Chongqing GDP

表1. 重庆GDP数据描述性统计量

3.1. 数据平稳性检验与处理

根据1978~2021年的重庆GDP数据，画出时间序列图如图1所示。

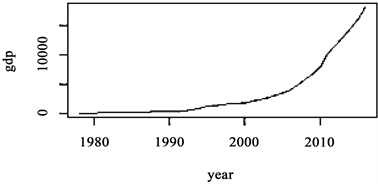
Figure 1. Time series of Chongqing GDP from 1978 to 2022

图1. 重庆GDP时间序列图(1978~2022)

Figure 2. ACF of Chongqing GDP

图2. 重庆GDP的ACF图

从图中可以看出，GDP的时间序列图呈现增长的趋势，并没有出现周期性和季节性的波动，ACF图(图2)也显示样本的衰减较慢，显而易见，这个时间序列明显是非平稳的，但无法直观判断这个非平稳时间序列属于随机游走(1)、带漂移(2)、带趋势项(3)的哪一类。

$\Delta y_t=\gamma {\gamma }_{t-1}+{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta y_{t-i}+{\epsilon }_i}$ (1)

$\Delta y_t=a+\gamma {\gamma }_{t-1}+{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta y_{t-i}+{\epsilon }_i}$ (2)

$\Delta y_t=a+\gamma {\gamma }_{t-1}+\delta t+{\displaystyle {\sum }_{i=1}^p{\beta }_i\Delta {\gamma }_{t-i}+{\epsilon }_i}$ (3)

在判断单位根时采用哪种检验式，本文使用urca程序包中ur.df函数进行检验式的判断与单位根的检验。首先对带趋势项的式子即(3)中设定进行检验，原假设，检验统计量值phi3为5.8679，phi3的1%，5%，10%的显著性水平下的临界值分别为9.31、6.73、5.61，即在5%的显著性水平下无法拒绝原假设，认为GDP时间序列不应该采用带趋势项的(3)式进行单位根检验。再对带漂移项的式子的(2)式进行单位根检验显示，检验统计量值phi2为5.1485，phi2的1%，5%，10%的显著性水平下的临界值分别为7.06、4.86、3.94，即在5%的显著性水平下拒绝原假设，认为GDP时间序列应该采用带趋势项的(2)式进行单位根检验。在此用检验式下单位根检验的tau2检验统计量值为2.99，tau2的1%，5%，10%的显著性水平下的临界值分别为−3.58、−2.93、−2.60，即5%的显著性水平下无法拒绝原假设，认为存在单位根，GDP时间序列是非平稳的。

对这个非平稳的序列进行第一次差分，得到一次差分后的时间序列如图3所示，图中有明显的增长趋势，ACF图(图4)仍然显示出样本的自相关性很强，初步说明序列是不平稳的，同样使用urca包中ur.df函数进行检验式的判断与单位根的检验。仍然对带趋势项的式子即(3)中设定进行检验，原假设，检验统计量值phi3为2.29，phi3的1%，5%，10%的显著性水平下的临界值分别为9.31、6.73、5.61，即在5%的显著性水平下无法拒绝原假设，认为GDP时间序列不应该采用带趋势项的(3)式进行单位根检验。再对带漂移项的式子的(2)式进行单位根检验显示，检验统计量值phi2为1.24，phi2的1%，5%，10%的显著性水平下的临界值分别为7.06、4.86、3.94，即在5%的显著性水平下无法拒绝原假设，认为GDP时间序列不应该采用带趋势项的(2)式进行单位根检验。最后对随走游走模型(1)式进行单位根检验显示，单位根检验的tau1检验统计量值为1.21，tau1的1%，5%，10%的显著性水平下的临界值分别为−2.62、−1.95、−1.61，即5%的显著性水平下无法拒绝原假设，认为存在单位根，一阶差分GDP时间序列是非平稳的。

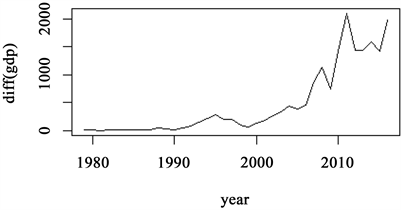
Figure 3. Time series of the first differenced series of GDP

图3. 一次差分后GDP时间序列图

对这个非平稳的GDP序列进行第二次差分，得到二次差分后的时间序列如图5所示，从图5可以看出序列是围绕0值上下波动的，ACF图(图6)显示出样本的自相关性已大大减弱，但需要进行单位根检验来验证。对带趋势项的式子即(3)中设定进行检验，原假设，检验统计量值phi3为2.29，phi3的1%，5%，10%的显著性水平下的临界值分别为9.31、6.73、5.61，即在5%的显著性水平下不能原假设，不认为GDP时间序列应该采用带趋势项的(3)式进行单位根检验。在用此检验式下单位根检验的tau3检验统计量值为−6.44，tau1的1%，5%，10%的显著性水平下的临界值分别为−4.15、−3.50、−3.18，即5%的显著性水平下拒绝原假设，认为不存在单位根，二阶差分GDP时间序列是平稳的。

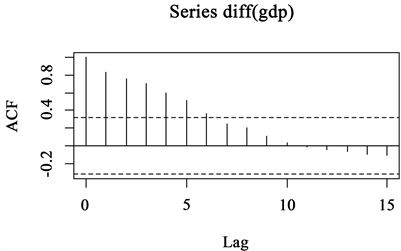
Figure 4. ACF of the first differenced series of GDP

图4. 一次差分后GDP的ACF图

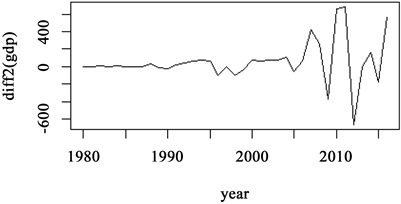
Figure 5. Time series of the second differenced series of GDP

图5. 二次差分后GDP时间序列图

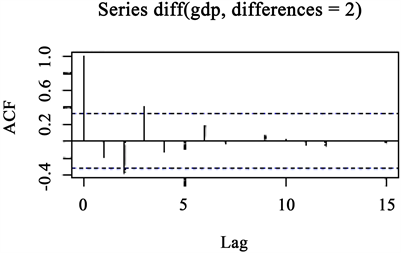
Figure 6. ACF of the second differenced series of GDP

图6. 二次差分后GDP的ACF图

3.2. 确定ARIMA模型的阶数

从上述分析得到，二次差分后的重庆GDP序列是平稳，对二次差分后序列进行ARIMA阶的确定与建模。用TSA程序包的EACF函数做EACF图(图7)，估计可能的p、q值。

Figure 7. Results of EACF

图7. EACF结果图

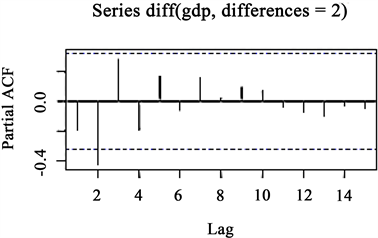
Figure 8. PACF of the second differenced series of GDP

图8. 二次差分后GDP的PACF图

从样本EACF图可以看到一个明显的倒三角区域，其左上方断点在AR = 1与MR = 2处，再结合ACF图与PACF图(图6，图8)所看到的图形形态，试着选择：ARIMA(1, 2, 2)，ARIMA(0, 2, 2)，ARIMA(0, 2, 3)，ARIMA(0, 2, 0)，ARIMA(1, 2, 3)，ARIMA(2, 2, 2)得到每个模型的AIC值见表，从表2中观察得到ARIMA(2, 2, 2)模型的AIC值最小，故使用ARIMA(2, 2, 2)模型来分析数据。

Table 2. Comparison of different ARIMA models

表2. 不同ARIMA模型比较

3.3. 模型的检验

模型的残差序列必须是白噪声说明模型是合适和充分的。本文利用ACF图和Ljung-box统计量检验残差是否符合白噪声。从残差的ACF图(图9)中看出样本的自相关函数值都在二倍标准差以内，说明无明显自相关。Ljung-Box统计量给出Q(5) = 0.44、Q(10) = 4.37，P值分别为0.66、0.44，均大于0.05，即在5%的水平下模型的残差并无显著的序列相关。从残差的ACF图和Ljung-Box统计量说明模型是合适和充分的。

Figure 9. ACF of residual series

图9. 残差的ACF图

Figure10. The fitted values (dashed line) and the actual observations (solid line) of GDP

图10. GDP的拟合值(虚线)与实际值(实线)

3.4. 拟合和预测

用拟合值(原始序列值 + 残差)的算法，将所有观察值的拟合值算出，并跟原始数列比较来检验模型的可靠性与准确性。图10显示模型和原始数据拟合很好，说明模型可靠的和准确的。

利用ARIMA(2, 2, 2)模型，预测2017~2021年的重庆GDP，预测结果如表所示，从表3分析可看到5年预测的平均误差仅为1.36%，模型的预测性能准确。图11显示利用R软体做出的模型5步向前预测值，即2017~2021的预测值与真实值的对比以及预测值95%置信的区间预测上下线。

Table 3. Comparison of the forecasts and actual observations in ARIMA(2, 2, 2)

表3. ARIMA(2, 2, 2)预测值与实际值的比较

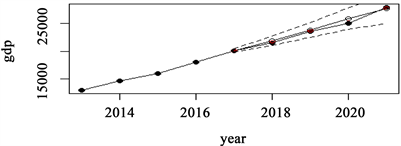
Figure 11. The forecasts (hollow circles) and actual observations (solid circles), and dashed lines show 95% interval forecasts from 2017 to 2021

图11. 2017~2021的预测值(空心)与真实值(实心)预测值95%的区间预测上下线(虚线)

4. 结语

ARIMA模型只能做短期的预测，在实际应用过程中，ARIMA模型预测短期的效果很好，但预测时间的延长会导致模型的误差变大。另外，ARIMA模型仍是一种传统的线性时间序列模型，预测时仅仅考虑从历史看未来，而没有加入可能影响未来的各种因素，如重庆新冠肺炎疫情的严重性对其GDP的影响，还有“一带一路”对重庆经济的影响，这些都是未来影响GDP增长的因素，也是模型中所无法体现出来的。因此用ARIMA模型只以历史数据做短期的预测，仅以用来参考 [3]。