高占比清洁能源下基于关联度的电网低周减载优化配置策略

Optimal Configuration Strategy of Under-Frequency Load Shedding for Power Grid Based on Correlation Degree under High Penetration Level of Clean Energy

摘要: 电力系统第三道防线中的低周减载是电网在遭受扰动后阻止系统频率快速持续下滑并最终维持系统频率稳定的重要措施之一。与此同时，大量清洁能源接入电网后，使得电网系统频率的特性变得更为恶化。如何在高占比清洁能源下探讨低周减载的优化配置方案是当前亟待解决的关键课题。为此，本文在大规模清洁能源接入电网的背景下，考虑因电源故障导致系统频率下降的情况，推导了能够有效实现减载的关联度指标，并在此基础上提出了一种基于关联度的电网低周减载优化配置策略。其中，利用改进场景分析方法来描述清洁能源的不确定性。进一步，提出了基于调节功率和稳态频率的低周减载方案整定流程。最后，以IEEE标准算例系统为例，通过仿真对比分析验证了所提出的电网低周减载优化配置策略的有效性。

Abstract: The under-frequency load shedding (UFLS) in the third line of defense of power system is one of the significant measures to prevent the rapid and continuous decline of the system frequency and ultimately maintain the stability of system frequency after disturbance. Meanwhile, when a large amount of clean energy is connected to the power grid, the frequency characteristics of the power system become worse. How to explore and exploit the optimal configuration strategy of UFLS under high penetration level of clean energy is a key issue to be solved urgently. Therefore, under the background of large-scale grid-connected clean energy, this paper deduces the correlation degree index which can effectively realize load shedding. On this basis, the improved scenario-based method is utilized to describe the uncertainty of clean energy. Further, the setting process of UFLS solution based on the adjustment power and steady-state frequency is proposed. Finally, taking the IEEE standard test system as an example, the validity of the proposed optimal configuration strategy of UFLS is verified by simulations and comparative analysis.

1. 引言

随着智能电网的快速发展以及“双碳目标”的提出，供需两端平衡的矛盾也日益凸显。特别是，随着大量清洁能源接入电网，系统惯量及调频能力被严重削弱，使得系统在遭受大扰动时导致频率进一步恶化 [1] [2]。如2019年8月的英国伦敦大停电事件 [3]，就是高占比清洁能源的接入致使英国电网系统惯量出现问题，削弱了电网抵御扰动的能力，同时扰动期间引发的低周减载动作是发生大停电的主因。而对我国而言，集中式清洁能源装机规模更大，某些区域电网发生扰动时由不平衡功率导致的低频问题更加突出。因此，如何有效制定适用于高占比清洁能源下低周减载优化配置策略一直是学术界和工业界研究的难点问题。

在我国第三道防线的紧急控制方法中，低周减载触发通常都是基于本地频率信息且分轮级进行。当地控制单元测量得到的频率达到事先设定的频率触发条件时，相应保护装置将按照整定好的动作轮级进行负荷切除操作，在现代电网的安全稳定运行控制中起到了至关重要的作用。众所周知，有效实现低周减载的关键环节为切负荷顺序及其相应的减载容量大小。迄今为止，国内外学者在此方面已开展了卓有成效的研究工作并取得了丰硕的研究成果。在切负荷顺序方面，有研究通过推导获得了系统惯量中心频率对于各负载切除容量大小之间的灵敏度关系 [4]，并由此可确定减载顺序和减载容量大小；有研究提出了一种甩负荷贡献因子的计算方法 [5]，该方法考虑了负荷重要性和电压特性，可实现在较小的减载量下频率的动态优化；有研究根据负载的随机和固定优先级的组合提出了一种低周减载技术 [6]，可在没有任何频率过调的情况下实现最佳减载；而在减载容量方面，有研究通过结合遗传算法与神经网络提出了一种优化的低压低频减载方法 [7]，可实现最小的切负荷量；除此之外，有研究提出了一种新的低周减载方案，该方案仅使用局部频率测量信息来估计惯量中心的频率变化率，并提出了一种拐点检测器技术来消除局部频率振荡的影响 [8]；有研究提出了一种连续低周减载方案 [9]，采用频率动力学的闭式解分析了所提出方案的特性；还有研究提出了一种仅靠本地负载信息来进行最优减载的方案，有效降低了对通讯条件及控制中心的依赖 [10]。随着清洁能源的快速发展，大规模并网的清洁能源对电力系统的频率特性带来了新的问题和挑战。有研究针对传统低周减载策略在高占比可再生能源系统应用中的不足，提出了一种基于频率变化率的多次甩负荷优化策略 [11]，实现了甩负荷量更少，频率恢复更加稳定；有研究针对高新能源占比电网，提出了基于df/dt的低周减载优化策略 [12]，为低惯量受端电网的频率稳定和第三道防线的协调配置提供参考；有研究对高风电渗透率的电网提出了一种自适应的低周减载方案 [13]，可有效改善负荷切除后的系统频率恢复效果以及负荷过切的概率；有研究以高风电占比的新疆电网为背景，提出了低周减载过程中动作频差和动作延迟的调整策略 [14]，可在满足频率要求的情况下尽可能减少减载量；还有研究考虑高占比可再生能源及储能系统下，提出了自适应的低周减载方法 [15]，其中考虑了合成惯量响应和储能容量限值的因素，可以实现更为精确和鲁棒的低周减载方案。现有研究虽然从不同角度对考虑高占比清洁能源的电网低周减载的优化配置方案进行了探讨，但对于低周减载过程中的减载顺序及减载容量大小两个关键问题的研究还需要进行更为深入、系统地思考和探究。

综上所述，本文提出了一种高清洁能源占比下基于关联度的电网低周减载优化配置策略。其中，针对因系统发电厂故障所导致的频率下降情况，理论推导了故障机组在正常运行时所输出的功率与各负荷所消耗功率之间的关系，并定义了相应的关联度指标；此外，利用一种改进的场景分析方法来描述风速预测误差的不确定性。在此基础上，为了提高低周减载的计算效率，提出了基于调节功率和稳态频率的两步骤低周减载方案整定流程。最后，以IEEE10机39节点算例系统为例对所提出的指标及低周减载方案整定策略进行了仿真和对比分析，结果验证了其合理性和有效性。

2. 关联度指标

2.1. 机组出力与负荷消耗功率关系

考虑到某电力系统因扰动出现功率供应不足时，如何能够找到造成该功率供应不足的故障机组在正常运行时的输出功率在各负荷所消耗功率之间的近似分配表达式，可以按分配该功率比重大小的顺序来依次切除负荷，从而可以实现以较小的减载量快速恢复频率的目的。假定所要研究的电网有n个节点m条支路，并且忽略输电线路中的电阻，则该网络节点电压方程的表达式如下：

$I_{\text{N}}\text{=}{Y}_{\text{N}}{U}_{\text{N}}$ (1)

式中： $I_{\text{N}}$ 、 $U_{\text{N}}$ 分别表示为节点注入电流和电压向量； $Y_{\text{N}}$ 表示为节点导纳矩阵。

同样地，电网支路电流向量 $I_{\text{B}}$ 的表达式如下：

$I_{\text{B}}\text{=}{Y}_{\text{B}}{A}^{\text{T}}{U}_{\text{N}}$ (2)

式中： $Y_{\text{B}}$ 表示为支路电纳矩阵，为对角阵； $A$ 表示为节点关联矩阵，是每列只有两个非零元素的稀疏矩阵。

根据公式(1)和公式(2)，可将电压向量 $U_{\text{N}}$ 消除，并且令 $C\text{=}{A}^{\text{T}}$，则可以得到：

$I_{\text{B}}\text{=}{Y}_{\text{B}}{A}^{\text{T}}{Y}_{\text{N}}^{\text{-1}}{I}_{\text{N}}\text{=}{Y}_{\text{B}}C{Z}_{\text{N}}{I}_{\text{N}}=\left[\begin{array}{ccc}{y}_1& & \\ & \ddots & \\ & & y_m\end{array}\right]\left[\begin{array}{ccc}{c}_{11}& \cdots & c_{1n}\\ ⋮& & ⋮\\ c_{m1}& \cdots & c_{mn}\end{array}\right]\left[\begin{array}{ccc}{z}_{11}& \cdots & z_{1n}\\ ⋮& & ⋮\\ z_{n1}& \cdots & z_{nn}\end{array}\right]\left[\begin{array}{c}{\stackrel{\dot{}}{I}}_{n1}\\ ⋮\\ {\stackrel{\dot{}}{I}}_{nn}\end{array}\right]$ (3)

式中： $Z_{\text{N}}$ 表示为电网的节点阻抗矩阵。

进一步假定某发电机组经升压变压器接入电网的示意图如图1所示。根据公式(3)，若令图1中升压变压器g的支路电纳为 $y_g$，则该升压变压器低压侧的支路电流 ${\stackrel{\dot{}}{I}}_{ab}$ (即发电机输出的电流)可被表示为如下各节点支路注入电流的线性组合：

${\stackrel{\dot{}}{I}}_{ab}={\displaystyle {\sum }_{j=1}^n{y}_g\left[{\displaystyle {\sum }_{l=1}^n{c}_{gl}{z}_{lj}}\right]{\stackrel{\dot{}}{I}}_{nj}}={\displaystyle {\sum }_{j=1}^n{\mu }_j{\stackrel{\dot{}}{I}}_{nj}}$ (4)

${\mu }_j=y_g{\displaystyle {\sum }_{l=1}^n{c}_{gl}{z}_{lj}}$ (5)

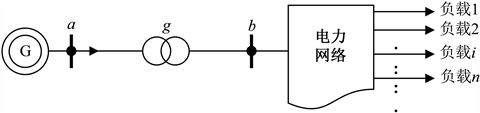
Figure 1. Diagram of a simplified power grid

图1. 一个简化电网示意图

为了将公式(4)所示的电流表达式转化为功率表达式，本文中将公式(4)两边取共轭，然后将分子和分母都乘以对应的节点电压向量，以使公式(4)左右两侧值保持不变，由此可得：

$\frac{{\tilde{I}}_{ab}{\stackrel{\dot{}}{U}}_a}{{\stackrel{\dot{}}{U}}_a}={\displaystyle {\sum }_{j=1}^n{\mu }_j\frac{{\tilde{I}}_{nj}{\stackrel{\dot{}}{U}}_j}{{\stackrel{\dot{}}{U}}_j}}$ (6)

式中： ${\stackrel{\dot{}}{U}}_a$ 、 ${\stackrel{\dot{}}{U}}_j$ 为节点a,j处的电压向量。

假定图1中变压器支路g传输的无功功率为Q_ab，节点j注入系统的有功功率和无功功率分别为P_j和Q_j，则公式(6)可以被写成如下功率形式的表达式：

$P_{ab}+j{Q}_{ab}={\displaystyle {\sum }_{j=1}^n{\mu }_j}\frac{\left(P_j+j{Q}_j\right){\stackrel{\dot{}}{U}}_a}{{\stackrel{\dot{}}{U}}_j}$ (7)

此外，根据电网正常运行时的电能质量的要求，本文假设电网中各节点电压都在其额定值附近波动，同时忽略图1中升压变压器的功率损耗，则公式(7)中有功功率部分(即图1中发电机组G的输出有功功率)的表达式可近似表示为：

$P_{ab}={\displaystyle {\sum }_{j=1}^n{\mu }_j\left[\cos \left({\delta }_a-{\delta }_j\right)-\tan {\phi }_j\sin \left({\delta }_a-{\delta }_j\right)\right]P_j}$ (8)

式中： ${\delta }_a$ 、 ${\delta }_j$ 为节点a，j处电压的相角； ${\phi }_j$ 为节点j处的功率因数角。

公式(8)说明了受扰动发电机组在正常运行时输出的功率可表示为各负荷消耗有功功率的线性组合。

2.2. 不平衡功率关联度优先级指标

基于公式(8)，本文假定该发电机组受扰动后发生脱网事故，并设该扰动编号为r，则第i个所允许切除的负载对该扰动r下导致的不平衡功率的关联度指标 ${\lambda }_{ri}$ 可定义如下：

${\lambda }_{ri}=\frac{{\mu }_i\left[\cos \left({\delta }_a-{\delta }_i\right)-\tan {\phi }_i\sin \left({\delta }_a-{\delta }_i\right)\right]}{{\displaystyle {\sum }_{j\in L}{\mu }_j}\left[\cos \left({\delta }_a-{\delta }_j\right)-\tan {\phi }_j\sin \left({\delta }_a-{\delta }_j\right)\right]}$ (9)

式中：L表示所有所允许切除的负载集合。

公式(9)的含义表示了受扰动后的发电机组脱网后，各允许被切除负载对系统不平衡功率的关联程度。该关联度指标值越大，表明该可被切除的负载与系统不平衡功率间的关系越“密切”，就应该被最先切除，反之，该负载被切除的顺序就越靠后。

公式(9)所定义的关联度指标是针对某一特定扰动r下的，而实际电网第三道防线中的低周减载的触发并非针对某特定扰动来进行整定，并且所允许切除负载的优先级顺序还需考虑多台发电机机组同时受扰动发生脱网的情况。因此，在上述分析的基础上，本文将多台发电机机组受扰动后同时脱网的故障视作为单台发电机组脱网的故障的组合。假定低周减载的扰动集合定义为F，第r个组合故障中的单台发电机组扰动为w，由此，本文定义如下：低周减载策略中与组合故障相关的第i个所被允许切除负荷的关联度优先级指标R_i为：

$R_i={\displaystyle {\sum }_{r\in F}{\displaystyle {\sum }_{w\in r}{p}_r\times P_{fw}\times {\lambda }_{wi}}}$ (10)

式中：p_r表示为组合故障r的发生概率；P_fw表示为单台发电机组扰动w造成的系统不平衡功率。

3. 基于改进场景法的清洁能源不确定性建模

本文研究中，高占比清洁能源的不确定性将通过场景分析法来进行建模。其中，高占比清洁能源主要考虑大规模风电。假定风速预测误差服从高斯分布，并设定期望值为0，标准差设为其预测值的10%。在此基础上，利用拉丁超立方抽样 [16] [17] 对风速预测误差的概率密度函数进行抽样，生成一组初始场景。之后，初始的风速场景集可以通过将风速预测值与该初始风速预测误差场景集进行相加得到。在得到初始风速场景集合后，本文采用一种改进的K-means聚类方法 [21] 来获取最终典型的风速场景集合。

3.1. 改进K-means算法

众所周知，传统的K-means算法主要包含以下两个步骤：1) 场景聚类；2) 场景选择。在场景聚类过程中，传统K-means算法是随机选取初始聚类中心，其结果是容易导致局部最优。为此，本文采用一种改进的最大最小距离算法 [18] 来确定初始聚类中心。

此外，场景选择的方法会影响典型场景集对原始场景集的逼近程度。目前，场景选择主要分为以下两种方法，即：均值选择和最大密度选择 [19]。它们都只使用子集中的信息，即只根据子集中的信息定义不同的典型场景，然后选择代表原始场景的典型场景。为了充分利用所有信息，使用认知科学领域的典型方法来选择子集的代表性场景 [20] [21]。一个对象与类成员越相似，与其他类成员越不相似，则该对象越具有代表性。因此，典型度被定义为内部相似性和外部不相似性的函数，以表征其在子集中的隶属程度。

综上，本文将引入最大最小距离算法和典型度思想对传统K-means算法进行改进，旨在使选取的典型场景集能更好地逼近原始场景集。该改进的K-means算法的具体实现步骤描述如下：

1) 场景聚类：在这里将采用改进的最大最小距离算法来确定初始聚类中心，具体过程为：

a) 计算初始场景集N中任意两个场景s_i，s_j间的Euclidean距离：

$d\left(s_i,s_j\right)=\Vert s_i-s_j\Vert ,s_i,s_j\in N$ (11)

b) 找到Euclidean距离中最小的两个场景 ${s^{\prime }}_i$ 和 ${s^{\prime }}_j$，并使用这两个场景的平均值 来替代它们：

$\bar{s}=\frac{{s^{\prime }}_i+{s^{\prime }}_j}{2},{s^{\prime }}_i,{s^{\prime }}_j\in N$ (12)

c) 重复上述过程(a)和过程(b)，直到剩余场景数目为事先设定的数目k，即为生成的初始聚类中心。在确定了初始聚类中心后，场景聚类的剩余过程都与常规K-means场景缩减方法一样。

2) 场景选择：在上述场景聚类步骤完成后，需在每个子集内选择最有代表性的场景作为典型的场景来代表整个子集。本研究中将引入一种典型度的思想来选择典型的场景，其具体计算过程描述如下：

a) 对于一个特定的子集c_u，利用下式计算表示其内部相似性的归一化因子Z_ru和表示外部不相似性的归一化因子Z_d：

$\{\begin{array}{l}diam\left(c_u\right)={\max }_{s_a,s_b\in c_u}\Vert s_a-s_b\Vert \\ Z_{ru}={\max }_{c_u}diam\left(c_u\right)\\ Z_d={\max }_{s_i,s_j\in N}\Vert s_i-s_j\Vert \end{array},u=1,2,\cdots ,k$ (13)

式中：s_a和s_b表示为特定子集c_u中任意的两个场景；s_i和s_j表示为初始场景集N中的任意两个场景。

b) 对于特定子集c_u中的任何一个场景s，定义相同子集内的其他场景作为其“朋友”场景，记作 $F=f{r}_1,f{r}_2,\cdots ,f{r}_i,\cdots ,f{r}_n$，则该特定子集内中每个场景s的内部相似性R(s)可表示为：

$R\left(s\right)=\frac{{\displaystyle {\sum }_{i=1}^n\left(1-\Vert s-f{r}_i\Vert \right)/Z_{ru}}}{n},s\in c_u$ (14)

c) 将特定子集c_u外部的所有其他场景看作为场景s的“反对者”场景，记作 $E=e_1,e_2,\cdots ,e_i,\cdots ,e_m$，则该特定子集内中每个场景s的外部不相似性D(s)可表示为：

$D\left(s\right)=\frac{{\displaystyle {\sum }_{i=1}^n\Vert s-e_i\Vert /Z_d}}{m},s\in c_u$ (15)

d) 根据公式(14)和公式(15)定义的内部相似性R(s)和外部不相似性D(s)，则可利用下式来计算特定子集内中每个场景s的典型度T(s)为：

$T\left(s\right)=\frac{R\left(s\right)\cdot D\left(s\right)}{R\left(s\right)\cdot D\left(s\right)+\left(1-R\left(s\right)\right)\cdot \left(1-D\left(s\right)\right)},s\in c_u$ (16)

e) 根据公式(16)选择典型度值最大的场景s_u来代表整个特定子集c_u，并利用下式来计算其概率 $p\left(s_u\right)$ 为：

$p\left(s_u\right)=\frac{U}{N_m},u=1,2,\cdots$ (17)

式中：U表示为特定子集c_u中的场景数量。

3.2. 风电场出力

在利用改进K-means方法获得最终典型的风速场景集合后，可利用公式(18)所示的分段函数来计算风速与风轮机出力之间的关系。计算中假定风电场拓扑为棋盘形式，并考虑风电场内的尾流效应。

$P_{WF}=\{\begin{array}{l}0v<\frac{v_{ci}}{\sqrt[3]{\zeta }}\text{or}v>v_{co}\\ \frac{v^3\cdot \zeta -v_{ci}^3}{v_r{}^3-v_{ci}^3}\cdot P_{wfr}\frac{v_{ci}}{\sqrt[3]{\zeta }}\le v<\frac{v_r}{\sqrt[3]{\zeta }}\\ P_{wfr}\frac{v_r}{\sqrt[3]{\zeta }}\le v<v_{co}\end{array}$ (18)

$P_{wfr}=n_{row}\cdot n_{col}\cdot P_{wt}$ (19)

式中：v为3.1节中得到的典型的风速场景集合中的风速；v_ci, v_co和v_r分别表示为切入风速、切出风速以及额定风速；n_row，n_col分别表示为棋盘式拓扑风场中风机排列的行数和列数；P_wt为单个风轮机的出力， $\zeta$ 为根据简森模型计算得到的尾流效应衰减系数 [22]。

至此，可求得每个风场出力典型场景下第i个被允许切除负荷的关联度优先级指标 $R_{is}$，公式(10)所定义的关联度优先级指标则进一步变为：

$R_i={\displaystyle {\sum }_{s=1}^{k}p\left(s\right)\cdot R_{is}}$ (20)

式中： $p\left(s\right)$ 为典型场景s的概率。

4. 含高占比清洁能源的低周减载方案优化配置

在低周减载方案整定过程中，首轮动作频率的阈值f₁、频差Δf以及频率动作延时Δt都是低周减载有效动作的关键参数。在本研究中，根据工程实际经验，通常将f₁、Δf和Δt的值分别设定为49.0 Hz、0.2 Hz以及0.2 s。为了有效提高低周减载的计算效率，本研究提出了基于调节功率和稳态频率的两步骤低周减载方案优化配置流程。

4.1. 定义调节功率

当电网中的发电厂受到扰动发生脱网故障时，系统中会产生大量的不平衡功率从而引发系统的功率–频率调节效应，进而导致系统频率下降。显然，该部分调节功率不能忽视，如能在低周减载方案优化配置过程加以考虑则可有效减少切负荷量。根据电网稳态运行时对电能质量的要求，系统的频率不应该低于49.8 Hz，再根据上述首轮动作频率阈值f₁的设定，因此本研究定义该调节功率P_re为：系统发生扰动时，不触发低周减载动作并且系统稳态频率能够自动恢复到49.8 Hz以上时的系统最大不平衡功率。在本研究中，P_re的具体值将针对具体算例系统通过仿真分析得到。

4.2. 两步骤法低周减载方案优化配置流程

根据2.2节所定义的关联度优先级指标，可将待切负荷按关联度值从大到小的次序生成甩负荷次序表。为了进一步有效提高低周减载仿真计算效率，本研究将低周减载方案优化配置过程分为两个步骤，即：步骤1：根据调节功率来获取近似的解；步骤2：根据稳态频率来获取最终的精确解。

4.2.1. 步骤1：获取甩负荷容量近似解

在步骤1中，首先将预先设定的故障集中所有故障按其故障功率P_f值的大小进行排列(从小到大次序)，其中每个故障下的近似的甩负荷容量P_tr可表示为：

$P_{tr}=P_f-P_{re}$ (21)

然后，在低周减载方案优化配置过程中每轮参与方案配置的故障都应该满足公式(22)给出的延时限制：

$\{\begin{array}{l}{t}_l\ge \Delta t\\ t_{l+1}<\Delta t\end{array}$ (22)

式中： $t_l$ 、 $t_{l+1}$ 分别表示为系统频率低于第l轮和第l + 1轮的系统频率动作阈值的时间。

接下来，根据上述生成的甩负荷次序表依相应的次序不断地追加负荷，直到甩负荷容量首次超过所有满足公式(22)所述延时限制的故障中最大的甩负荷容量P_tr为止。

4.2.2. 步骤2：获取甩负荷容量精确解

在上述步骤1中所获取的满足一定条件的甩负荷容量的近似解只是满足相应的轮级约束，而对于低周减载动作后系统的稳态频率无任何限制，故而容易导致负荷过切或者欠切的现象。因此，本研究将公式(23)给出来的低周减载动作后的系统稳态频率 $f_{\infty }$ 约束当作求取甩负荷容量精确解的依据，即：

$49.8\text{Hz}\le f_{\infty }\le 50.2\text{Hz}$ (23)

根据公式(23)，如果系统低周减载动作后，系统稳态频率小于49.8 Hz，即导致了负荷欠切现象，此时应再追加甩负荷次序表中的负荷进行减载直到系统的稳态频率满足公式(23)；反之，如果系统稳态频率大于50.2 Hz，即导致了负荷过切现象，此时应将步骤1所获取的甩负荷近似解中的减载次序靠后的负荷去掉，直到系统稳态频率满足公式(23)。

综上所述，高清洁能源占比下基于关联度的电网低周减载优化配置策略流程图如图2所示。

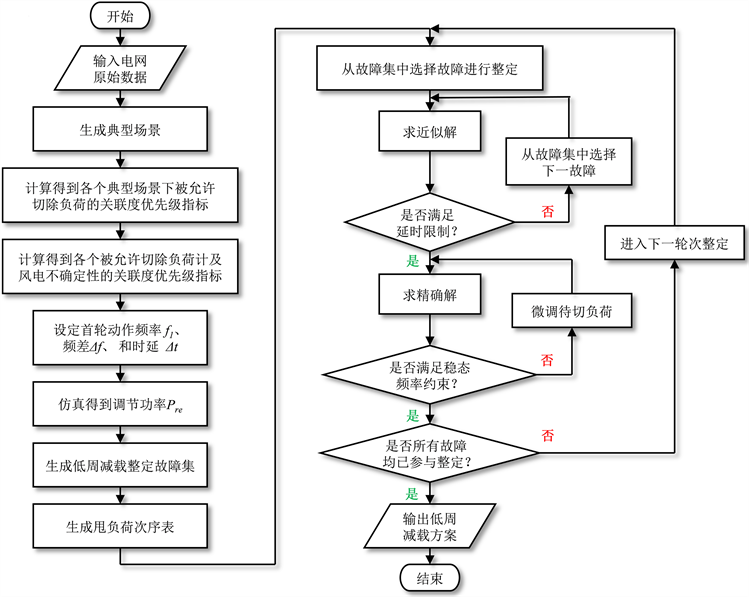
Figure 2. Flowchart of optimal configuration strategy of under-frequency load shedding for power grid based on correlation degree under high penetration level of clean energy

图2. 高清洁能源占比下基于关联度的电网低周减载优化配置策略流程图

5. 算例仿真分析

本文以IEEE10机39节点算例系统为例对所提出的指标及低周减载方案整定策略进行仿真和对比分析，来验证其合理性和有效性。其中，节点30、节点32、节点33、节点34所连机组为风电机组，其额定总出力为2040 MW，占整个系统额定总出力的32.9%，如图3所示。此外，风电场的切入风速v_ci、切出风速v_co以及额定风速v_r分别为3.5 m/s、25 m/s和13.5 m/s，尾流效应衰减系数 $\zeta$ 为0.9226，并将风速预测值设定为9.466 m/s，初始场景N设定为3000，典型场景数设定为10。

此外，将除了接入平衡节点32的机组以外的9个机组作为可能发生故障的机组，假设最多两台机组同时发生故障，则故障集中一共有 ${\text{C}}_9^1+{\text{C}}_9^2=\text{45}$ 个故障，造成的最大不平衡功率为1830 MW；进一步，设定被允许切除负荷为节点7、节点12、节点18、节点21、节点23、节点25、节点26、节点27、节点28、节点31，总计容量1781 MW。

Figure 3. Wiring diagram of modified IEEE 39-bus test system

图3. 修改后的IEEE 39节点测试系统接线图

5.1. 验证关联度指标

由前文分析可知，关联度指标是后续研究的关键，也是关联度优先级指标的基础。现假设接入节点30的机组发生故障脱网，挑选出针对该扰动关联度指标最高、居中以及最小的允许切除负荷，即节点25、节点27和节点12在扰动发生后相同时间切除相同容量的负载，得到的系统频率如图4所示。由图4可以看出，在切除相同容量的情况下，切除关联度指标越大的负荷，其动态过程中的暂态最低频率越高、暂态最高频率越低、稳态频率越高。这表明切除关联度指标大的负荷后，系统的波动更小，降低了增加减载轮次以及触发高周切机的风险，并且当系统达到稳态时能有更好的频率恢复效果，与切除关联度指标小的负荷相比，能相对地减少甩负荷的容量，验证了所提关联度指标的正确性，为后续的方案整定提供了有效基础。

Figure 4. Frequency curves after shedding different loads with the same capacity

图4. 相同容量下甩掉不同负荷后的频率曲线

5.2. 验证关联度优先级指标

根据前文所提方法整定得到低周减载的优化方案如表1所示，共有6轮，总甩负荷容量1781 MW。

Table 1. System simulation result data of IEEE 39-bus test system

表1. IEEE 39节点测试系统仿真结果数据

对于本文中最极端的扰动，系统将产生1830 MW的不平衡功率，按表1所示的方案在系统受到此扰动甩负荷后，系统的频率曲线如图5所示，系统的稳态频率为49.895 Hz，满足稳态频率约束，系统恢复稳定，证明了按照本文所提方法正定得到的低周减载方案具有可行性和有效性。

进一步，为验证本文所提方法的优越性，随机生成允许切除负荷的顺序以替代本文中的甩负荷次序表，整定得到一套“随机方案”，并将上述45个基本故障聚类生成6个典型故障，对比两套方案在系统发生典型故障触发动作后的暂态最低频率和暂态最高频率，如图6所示。从图6可以看出，除了第一个典型故障(该故障下两套方案均未触发低周减载动作)外，优化方案的暂态最低频率均高于随机方案，优化方案的暂态最高频率均低于随机方案，进一步验证了本文所提方法的优越性。

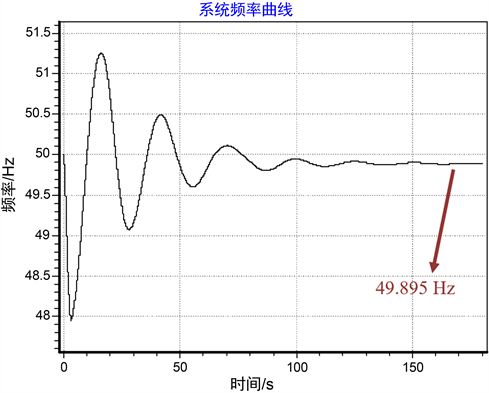
Figure 5. Frequency curve after UFLS is triggered for the most extreme fault

图5. 最极端故障下低周减载出发后的频率曲线

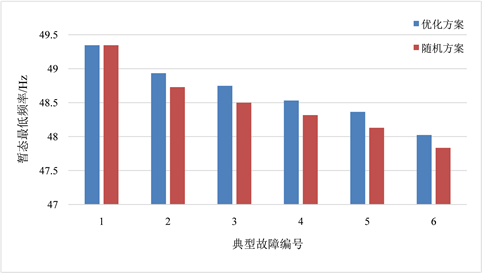
Figure 6. Comparisons of the transient frequency

图6. 暂态频率比较

5.3. 高占比清洁能源对低周减载策略的影响

当节点34所连风电场和节点35所连常规机组分别损失相同出力500 MW而触发表1所示低周减载方案后，动作的情况如表2所示。可以看到，当扰动来自风电场时，系统暂态最低频率较高、暂态最高频率较低、稳态频率较高，这是系统保留更大转动惯量以及旋转备用带来的必然结果。

Table 2. Comparisons of the simulation results after UFLS with high penetration level of clean energy (32.9%)

表2. 高占比清洁能源下低周减载动作情况对比(32.9%)

进一步，将节点38所连常规机组替换为等额定容量的风电场，以至风电的额定总出力为2870 MW，占整个系统额定总出力的46.4%。此时仍使节点34和节点35分别损失出力500 MW后触发低周减载动作，此时的动作情况如表3所示。对比表2和表3，可以明显看到当系统风电的渗透率提高以后，虽然最终频率可以恢复至49.8 Hz以上，但同一故障下的减载轮次增加，系统波动明显增大。

Table 3. Comparisons of the simulation results after UFLS with high penetration level of clean energy (46.4%)

表3. 高占比清洁能源下低周减载动作情况对比(46.4%)

6. 结论

本文基于理论推导得出衡量负荷与不平衡功率之间关系的关联度指标，并基于此进一步得到被允许切除负荷在低周减载整定过程中的关联度优先级指标。对于风电功率的不确定性，引入最大最小距离算法和典型度思想改进了传统的K-means算法，使得到的典型场景集能更好地逼近原始场景集。并为了有效提高计算效率，将求解过程分为求取近似解和精确解两步。最后，以不同清洁能源渗透率的IEEE10机39节点系统为例，验证了所提指标以及整定方法的合理性和有效性，并得出以下结论：

1) 当电网受到扰动产生不平衡功率时，切除与此不平衡功率关联度指标较高的负荷，可以在相同甩负荷容量的基础上相较于其他负荷得到更好的动作效果，相对地减少了减载容量，故应优先切除。

2) 本文所提出的基于关联度的低周减载优化配置策略可以有效地减小电网暂态频率的变化范围，更有利于电网稳定。

3) 对高占比清洁能源对低周减载带来的影响展开研究，发现损失常规机组出力给高新能源渗透率电网带来的波动更大，对低周减载方案的要求更高，当系统新能源渗透率进一步增加后尤其明显。