洞庭湖流域水系汛期分期研究

Study on Flood Season Segmentation of Dongting Lake Basin

摘要: 汛期分期是推求分期设计洪水和分期汛限水位的基础。本文综合运用天气成因分析和5种数理统计方法对洞庭湖流域的湘江、资江、沅江和澧水水系进行了汛期分期。研究结果表明：洞庭湖流域汛期(5月1日~10月31日)可划分为前汛期、主汛期和后汛期。湘江、资江、沅江、澧水的主汛期分别为6月15日~7月23日、6月14日~7月28日、6月20日~8月2日、6月22日~8月9日。汛期分期可合理表征流域洪水季节性特征，为充分挖掘流域洪水资源化潜力提供支撑。

Abstract: Flood season segmentation is the basis for estimating seasonal design flood and seasonal flood limit water levels. The cause analysis method and five mathematical statistics methods were applied to the flood season segmentation of Xiangjiang, Zijiang, Yuanjiang and Lishui rivers in the Dongting Lake basin. The results illustrated that the flood season (1 May~31 October)could be segmented into the early flood season, the main flood season and the late flood season. The main flood seasons of Xiangjiang, Zijiang, Yuan- jiang and Lishui rivers are 15 June~23 July, 14 June~28 July, 20 June~2 August and 22 June~9 August, respectively. These results are reasonably characterized the flood seasonality and could provide support for exploiting the potential of flood water resources utilizing.

1. 引言

洞庭湖流域位于我国长江中游以南，是长江重要的调蓄型湖泊之一，在长江中下游防洪调蓄占据重要地位 [1]。受全球气候变化与强人类活动影响，洞庭湖流域面临洪涝风险与干旱缺水并存的问题 [2]。洞庭湖流域主要支流湘江、资江、沅江、澧水等建有众多大型水库，汛期持续时间长且洪水频发 [1] [3]。如果水库在汛期仅采用单一汛限水位调度，无法充分利用汛期洪水资源，易导致汛末蓄水率偏低 [4]。汛期分期作为分期设计洪水和分期汛限水位计算的重要内容，通过研究流域汛期季节性规律，将汛期划分为前汛期、主汛期和后汛期，对实现水库洪水资源化、提高流域供水能力具有重要意义。

国内学者根据洪水的季节性特征，在流域汛期分期的研究和实践中进行了积极探索。汛期分期的常用方法可以分为定性分析法和定量计算法 [5]。其中定性分析法以天气成因法为代表，能综合考虑多种成灾天气因素，可靠性较高，但分期时段难以细化到日，结果较为粗略，在实践中通常与定量计算方法结合使用 [6]。定量计算法又以数理统计方法为主，可以分为统计分析法和聚类分析法。统计分析法原理简单，概念清晰，但分期精度一般较低，常用的有圆形分布法 [7]、相对频率法 [8] 等；聚类分析法则有一定的数学物理背景支撑，但计算存在主观性，常用的方法有变点分析法 [9] [10]、模糊集合分析法 [11]、分形分析法 [12]、信息熵法 [13]、有序聚类法 [14] 等。这些定量方法各有优缺点，在计算过程中带有一定的主观性或局限性 [15]。不同方法得到的汛期分期结果有所差异，尚未形成一种公认的方法 [16]。因此有必要综合运用定量分期方法与定性方法以确定合理可靠的汛期分期方案。

近年来洞庭湖流域旱涝灾害频繁，加剧了水库防洪与兴利之间的矛盾，成为制约当地可持续发展的重要因素 [2]。汛期分期可合理表征流域洪水季节性特征，为充分挖掘流域洪水资源化潜力提供支撑，但目前尚没有针对洞庭湖流域开展汛期分期研究。鉴于此，本文将结合天气成因分析与流域洪水分布与径流分析，并综合运用变点分析法、信息熵法、有序聚类法、圆形分布法、相对频率法等多种数理统计方法，从定性与定量两方面对洞庭湖流域的四水水系进行汛期分期，给出合理可靠的汛期分期方案，为实现洞庭湖流域水库群洪水资源化提供基础支撑。

2. 研究方法

2.1. 变点分析法

变点分析可用于研究某一时间序列经分割前后两段的统计量是否发生变化以及变化的位置、幅度等。常用的变点分析方法较多，均值变点法与概率变点法于汛期分期领域有较成熟的应用。

均值变点分析法的研究对象是系列长度为n的流(洪)量样本 $X_i$，并做出数据服从正态分布且相互独立两个基本假设。

$\begin{array}{cc}{X}_i={\mu }_i+e_i,& i=1,2,\cdots ,n\end{array}$ (1)

如果存在

${\mu }_1={\mu }_2=\cdots ={\mu }_{m_1-1}=b_1,{\mu }_{m_1}={\mu }_{m_1+1}=\cdots ={\mu }_{m_2-1}=b_2,\cdots ,{\mu }_{m_q}={\mu }_{m_q+1}=\cdots ={\mu }_n=b_{q+1}$ (2)

式中， ${\mu }_i$ 为 $X_i$ 的期望值，随机误差项 $e_i$ 等方差且期望值为0，q是变点个数， $m_j\left(j=1,2,\cdots ,q\right)$ 为变点位置，且 $1<m_1<m_2<\cdots <m_q\le n$， $b_i\left(i=1,2,\cdots ,q+1\right)$ 是各分期的均值。

如果 $m_j$ 前后分期的均值不相等，即 $b_j\ne b_{j+1}$，则 $m_j$ 就是一个变点。根据这一原理，采用最小二乘法寻找变点位置。给出变点个数q和初步估计的变点位置，给定 $m_0=1$ 及 $m_{q+1}=n+1$ ；在 $\left(m_{j-1},m_{j+1}\right)$ 区间内反复变动 $m_j$，计算第j分期均值 $b_j$ 的初步估计值 $y_j$ 并使函数 $W_j$ 达到极小值：

$y_j=\frac{x_m{}_{{}_{j-1}}+x_{m_{j-2}}+\cdots +x_{m_j}{}_{-1}}{m_j-m_{j-1}}$ (3)

$\begin{array}{cc}{W}_j={\displaystyle \underset{i=m_{j-1}}{\overset{m_j-1}{\sum }}{\left(x_i-y_j\right)}^2}+{\displaystyle \underset{i=m_j}{\overset{m_{j+1}-1}{\sum }}{\left(x_i-y_{j+1}\right)}^2},& j=1,2,\cdots ,q\end{array}$ (4)

以此类推，直到找到所有q个变点。为了检验变点 $m_j$ 是否存在于 $\left(m_{j-1},m_{j+1}\right)$ 区间，取检验显著性水平 $\alpha$，用下式估算样本方差 ${\sigma }^2$，进而计算统计量 $C_{\alpha }$ 和T：

${\sigma }^2=\frac{W_j}{N-2\log \log N-\log \log \log N-2.4}$ (5)

$C_{\alpha }={\sigma }^2\left(2\log \log N+\log \log \log N-\log \pi -2\log \left(-0.5\log \left(1-\alpha \right)\right)\right)$ (6)

$T={\displaystyle \underset{i=m_{j-1}}{\overset{m_{j+1}-1}{\sum }}{\left(x_i-\bar{X}\right)}^2}$ (7)

式中，N为变点 $m_j$ 前后两分期的总长度， $\bar{X}$ 为变点 $m_j$ 前后两分期序列的均值。

若 $T-W_j>C_{\alpha }$，则认为在显著性水平 $\alpha$ 上，变点 $m_j$ 存在。

概率变点分析法通过统计洪水事件的发生次数，判别在未知点m前后概率是否突变。假设流域汛期长度为T天，对n年实测资料，概率变点分析方法假定每天洪水发生次数 $x_i\left(i=1,2,\cdots ,T\right)$ 服从二项式分布且相互独立。与均值变点的做法相似，先给定变点的个数和初始估计，变点 $m_j\left(j=1,2,\cdots ,q\right)$ 可根据极大化似然函数来寻找：

$L={\displaystyle \underset{i=1}{\overset{m_1-1}{\prod }}{C}_n^{x_i}{p}_1^{x_i}{\left(1-p_1\right)}^{n-x_i}}{\displaystyle \underset{i=m_1}{\overset{m_2-1}{\prod }}{C}_n^{x_i}{p}_2^{x_i}{\left(1-p_2\right)}^{n-x_i}}\cdots {\displaystyle \underset{i=m_q}{\overset{m_{q+1}-1}{\prod }}{C}_n^{x_i}{p}_{q+1}^{x_i}{\left(1-p_{q+1}\right)}^{n-x_i}}$ (8)

式中，n为实测资料年数， $p_i$ 表示在第i分期中洪水事件发生的概率，可用下式估计：

$p_i=\frac{1}{n\left(m_i-m_{i-1}\right)}{\displaystyle \underset{j=m_{i-1}}{\overset{m_i-1}{\sum }}{x}_j}$ (9)

考虑到分期方案比选时仅需比较极大化函数值的大小，且式(8)计算时可能引起数值溢出，可以将极大化函数改为下式：

$L^{\prime }={\displaystyle \underset{i=1}{\overset{q+1}{\sum }}{\displaystyle \underset{j=m_{i-1}}{\overset{m_i-1}{\sum }}{x}_j\log p_i}}+{\displaystyle \underset{i=1}{\overset{q+1}{\sum }}{\displaystyle \underset{j=m_{i-1}}{\overset{m_i-1}{\sum }}\left(n-x_j\right)\log \left(1-p_i\right)}}$ (10)

同样，要对概率变点分期结果进行假设检验，判定分期是否成立。更为通用的秩和检验法或游程检验法可以用于上述两类变点分析法的假设检验 [9]。

2.2. 有序聚类法

汛期划分可以看作一个根据时间序列前后段的特征相似性进行归类的样本聚类分析问题 [14]。在分类时保持时间序列次序，这样的分类称为有序分类。以有序分类来推求最优分割点，其实质是使同类的离差平方和较小，而各类间的离差平方和较大。

给定分期数k，对于第j分期来说，该分期的离差平方和 $S_j$ 表示为：

$S_j={\displaystyle \underset{i=m_j}{\overset{m_{j+1}-1}{\sum }}{\left(X_i-{\bar{X}}_j\right)}^2}$ (11)

式中， $m_j$ 为第j分期开始点的位置， $X_i$ 为样本第i天的流(洪)量， ${\bar{X}}_j$ 为第j分期序列的均值。

$S^{*}={\displaystyle \underset{j=1}{\overset{k}{\sum }}{S}_j}$ (12)

将各分期离差平方和相加得到 $S^{*}$， $S^{*}$ 越小则分期越合理。通过改变各分期点位置，计算所有可能的分期方案对应的 $S^{*}$，使之达到最小的分类方案视为样本的最优分割方案。

2.3. 信息熵法

信息熵法通过计算水文时间序列均匀度进行流域的汛期划分，既要考虑同一分期内的均质性，又要区分不同分期间的差异 [13]。对于系列长度为n的流(洪)量样本 $X_i$，给定分期数k，故第j分期的流(洪)量和 $S_j$ 为：

$\begin{array}{cc}{S}_j={\displaystyle \underset{i=m_j}{\overset{m_{j+1}-1}{\sum }}{X}_i},& j=1,2,\cdots ,k\end{array}$ (13)

式中， $m_j$ 为第j分期开始点的位置， $X_i$ 为第i天的流(洪)量。

将每一分期视为一类，第j分期内第i日流(洪)量值 $X_i$ 在该类的占比 $P_i$ 为：

$\begin{array}{cc}{P}_i=\frac{X_i}{S_j},& i=m_j,m_j+1,\cdots ,m_{j+1}-1\end{array}$ (14)

由信息熵的定义，得到第j分期的信息熵 $H_j$ 为：

$H_j=-{\displaystyle \underset{i=m_j}{\overset{m_{j+1}-1}{\sum }}{P}_i\log P_i}$ (15)

当该分期的每日洪峰值的占比均相等时达到信息熵的最大值，即：

$P_{m_j}=P_{m_j+1}=\cdots =P_{m_{j+1}-1}\Rightarrow H_{\max ,}{}_j=\log \left(m_{j+1}-m_j\right)$ (16)

式中， $H_{\max ,}{}_j$ 为第j分期信息熵的最大值。

各分期均匀度 $U_j$ 为：

$U_j=\frac{H_j}{H_{\max ,}{}_j}$ (17)

$U_j$ 描述了分期内流(洪)量时间序列的均匀程度， $U_j$ 越大，代表该分期的均匀程度越高 [13]。如果某一分期持续时间更长，则该分期对汛期整体均匀程度的影响更大 [13]，因此以分期长度为权重计算总体的加权均匀度：

$U=\frac{m_1}{n}{U}_1+\frac{m_2-m_1}{n}{U}_2+\cdots +\frac{n-m_{j-1}}{n}{U}_k$ (18)

通过遍历各分期点的位置，直到加权均匀度取得所有分期方案中的最大值，此时的分期方案被认为是最合理的。

2.4. 圆形分布法

圆形分布法是通过三角函数变换将洪水发生事件化为矢量，进而计算矢量特征值寻找分期点的一种统计方法。设汛期长度为T天，洪水样本容量为N，其中第i场洪水的发生时间和量级为 $D_i$ 和 $q_i$，通过下式转换为直角坐标系中的点 $\left(x_i,y_i\right)$ ：

${\alpha }_i=\frac{2\pi D_i}{T}$ (19)

$\left(x_i,y_i\right)=\{\begin{array}{ll}\left(\cos {\alpha }_i,\sin {\alpha }_i\right)\hfill & 不考虑洪水量级\hfill \\ \left(q_i\cos {\alpha }_i,q_i\sin {\alpha }_i\right)\hfill & 考虑洪水量级\hfill \end{array}$ (20)

式中， ${\alpha }_i$ 为第i场洪水对应矢量的角度， $0\le \alpha \le 2\pi$。

汛期发生洪水的集中期 $\bar{\alpha }$ 和集中度r分别为：

$\bar{\alpha }=\{\begin{array}{ll}\arctan \frac{\bar{y}}{\bar{x}}\hfill & x>0\hfill \\ 2\pi +\arctan \frac{\bar{y}}{\bar{x}}\hfill & x<0\hfill \end{array}$ (21)

$r=\{\begin{array}{ll}\sqrt{{\bar{x}}^2+{\bar{y}}^2}\hfill & 不考虑洪水量级\hfill \\ \frac{\sqrt{{\bar{x}}^2+{\bar{y}}^2}}{Q}\hfill & 考虑洪水量级\hfill \end{array}$ (22)

式中，Q表示N场洪水流(洪)量之和，即 $Q={\displaystyle \underset{i=1}{\overset{N}{\sum }}{q}_i}$。

集中度r是圆形分布法中描述 ${\alpha }_i$ 集中趋势的指标，它与 ${\alpha }_i$ 的标准差s有如下转换关系：

$s=\sqrt{-2\ln r}$ (23)

据此可得主汛期起止时间 $D_s$ 和 $D_e$ 分别为

$D_s=\frac{\bar{\alpha }-s}{2\pi }T$ (24)

$D_e=\frac{\bar{\alpha }+s}{2\pi }T$ (25)

2.5. 相对频率法

相对频率法是按照月(或旬)统计时段内发生洪水的频率，通过分析汛期各时段洪水发生频率的变化特征，将大小接近的时段归为同一分期，得到汛期的分期方式 [17]。

假设汛期时段数为T，日均流量资料n年，统计洪水在各分期的发生次数。各时段的相对频率 $R{F}_i$ 计算公式为

$\begin{array}{cc}R{F}_i=\frac{b_i}{n},& i=1,2,\cdots ,T\end{array}$ (26)

式中， $R{F}_i$ 表示第i时段的相对频率； $b_i$ 表示洪水在第i时段出现的次数；n为资料总年数。

为了实际应用方便，常将时段长细分到旬。由于各旬天数不等(某些下旬有11天)，为使所有旬统一为10天，在计算相对频率时需乘以时间系数以作调整，如8月下旬有11天，因此将旬频率乘以系数10/11。但是初始频率 $R{F}_i$ 的代数和s与调整之后的频率 $R{F^{\prime }}_i$ 总和 $s^{\prime }$ 不相等，因此做如下处理：

$\begin{array}{cc}R{F}_i=R{F^{\prime }}_i\cdot \frac{s}{s^{\prime }},& i=1,2,\cdots ,T\end{array}$ (27)

式中， $R{F^{\prime }}_i$ 为对天数不同的时段做调整后的第i时段的相对频率，s为式(26)计算的各时段初始频率代数和， $s^{\prime }$ 为调整后的各时段频率代数和。

对经式(27)的调整后的各分期相对频率 $R{F}_i$ 进行比较，把大小接近的时段划分为同一分期。

3. 研究区域

3.1. 流域概况

洞庭湖流域总面积达26.3万km²，占长江流域面积的14.6%，是我国面积第二大、蓄水量第一大的淡水湖泊。其西南侧长江一级支流湘江、资江、沅江、澧水四水经洞庭湖调蓄，由岳阳市城陵矶注入长江。洞庭湖流域位于亚热带季风气候区，降雨充沛、水量丰富，然而降水季节分布不均，汛期降水量约占全年的65%以上 [18]。四水多年平均径流量共计1644.5 亿m³，占城陵矶出口径流量的59.7%，是洞庭湖流域上游来水的主导因素。洞庭湖流域水系与水文站分布如图1所示。

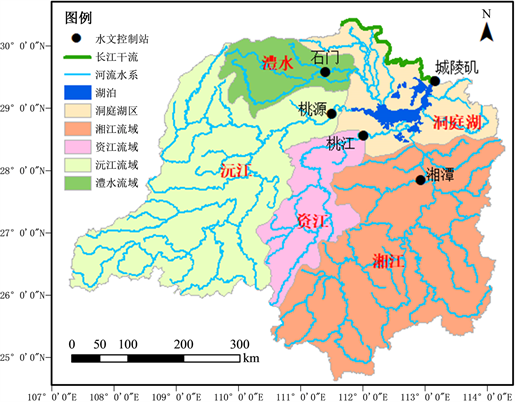
Figure 1. Sketch map of the Dongting Lake basin and hydrologic stations

图1. 洞庭湖流域水系与水文站示意图

本文研究的湘–资–沅–澧四水流域的分布的骨干防洪水库基本情况见表1。流域的汛期时间域是5月1日~10月31日。研究选用的基本资料为四水流域出口控制站湘潭站1988年~2020年、石门站1950年~2020年、桃源与桃江站1951年~2020年汛期逐日平均流量资料。

Table 1. Basic information of the Four Rivers basin and main reservoirs

表1. 洞庭湖四水流域与主要水库基本情况

3.2. 取样方法

在汛期分期研究中，往往需要从N年流量资料取样得到一维时间序列。本研究取样方法采用日最大值取样、超定量(POT)取样和年最大值(AM)取样三种取样方法 [9]。日最大值取样是对于某一日，选出N年中该日的最大洪峰(量)构造的时间序列，序列长度等于汛期长度。POT取样是设定门限值，选取N年流量资料中超过该门限值的洪峰(量)值构成新序列。AM取样是从N年流量资料中选出每年最大的洪峰(量)及其发生时间构成的时间序列。

日最大值取样和POT取样一定程度上忽略了较枯年份，仅考虑系列资料中当日最大或满足门限值的数据；AM取样可以综合考虑来水较枯和洪水多发的情况，但得到的样本长度与资料年数有关。因此，本文通过门限值的选取控制POT取样得到的洪水场次为资料年数的2~3倍，以平衡各取样方法的优劣。在样本时段长度方面，本研究选择了洪峰流量、3日洪量、7日洪量等三类样本进行了计算，不同样本的分期结果基本一致。为避免人为分割误差，在3日(或7日)洪量样本的日最大值取样中以第2日(或第4日)为中心。

各分期方法采用的取样方式、时段长和POT阈值在表2中列出。变点分析法的检验显著性水平设为0.05，湘江、沅江与澧水流域采用日最大洪峰流量序列为样本；资江流域的日最大洪峰流量、三日洪量序列计算结果均未通过假设检验，因此选择日最大七日洪量序列为样本。在概率变点法中各流域的POT门限值根据取样序列服从二项式分布的原则试算获得。此外，为防止运用有序聚类法计算离差平方和的数值溢出，先对时间序列进行标准化处理 [14]。

Table 2. The sampled series of each segmentation method

表2. 各分期方法的取样序列

4. 结果分析

4.1. 天气成因分析

天气成因分析通过研究西太平洋副热带高压(下面简称副高)活动、热带环流及大气中的水汽等因素对流域降水的动力条件和水汽供应条件影响进行汛期划分 [19]。洞庭湖流域亚热带季风气候特点明显，受到副高活动的显著影响。

副高是决定梅雨锋系及其降雨带位置的主要天气系统之一，当副高脊线停留在20˚N~25˚N之间时，梅雨位置常处于洞庭湖流域范围内 [20]。此外，厄尔尼诺现象等大气环流异常会影响副高的强度和位置。副高位置的偏南偏西会促进梅雨期暖湿气流向长江中游转移，致使长江中下游地区降水偏多 [20]。如1997年发生的20世纪最强的厄尔尼诺现象，导致次年的汛期副高强度增强，位置也有所变化，副高脊线于6月中下旬和7月下旬两度在15˚N~23˚N之间徘徊，致使副高北侧边缘强降雨带长时间在长江流域维持，因此副高异常成为1998特大洪涝灾害的重要因素。副高脊线在20˚N~25˚N间停留时间长短直接影响了洞庭湖流域汛期降水。1951年~2021年西太平洋副高脊线位置指数(500 hPa高度场，10˚N~60˚N、110˚E~150˚E区域内逐条经线上副高中心位置所在纬度的平均值)的月平均值与流域纬度边界的关系如图2所示。自6月份西太平洋副高脊线进入20˚N~25˚N区间，四水流域降水主要集中在6月~8月，以6月降水量最多，可将流域主汛期初步判定为6月~8月。

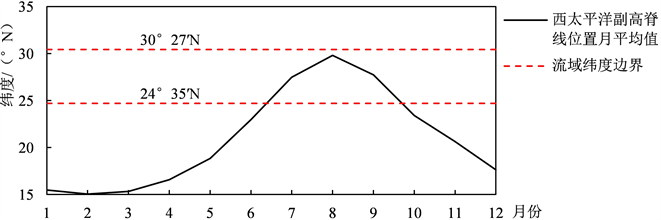
Figure 2. Monthly average of Western Pacific subtropical high ridge line index

图2. 西太平洋副高脊线位置指数月平均值

4.2. 汛期洪水分布与径流分析

4.2.1. 汛期洪水年内分布分析

根据洞庭湖三支流的汛期径流资料，统计分析了汛期洪水的年内分布特征。以沅江桃源站为例，表3展示的是洪峰流量在10,000 m³/s以上的共计403场洪水在汛期各旬的分布。洪峰流量大于25,000 m³/s的洪水共有6场，其中5场集中出现在7月中旬；洪峰超过20,000 m³/s的洪水共有26场，自6月下旬开始出现，其中25场发生于6月下旬到7月下旬之间；洪峰流量在10,000~20,000 m³/s的洪水共计377场，其中87%的场次发生在5月到7月之间，并有77场集中发生在6月下旬。从时间上看，6、7月发生洪水场次最多，达到277场；8月洪水场次较前月有76.7%的下降。从8月中旬到10月下旬洪水仅有38场，且从8月中旬的12场逐渐减少到10月的5场。

Table 3. Flood distribution of Taoyuan station in Yuanjiang River during flood season from 1951 to 2020

表3. 沅江桃源站1951~2020年汛期洪水分布

4.2.2. 汛期径流统计分析

湘江、资江、沅江和澧水的汛期多年平均流量分别为2498 m³/s、862 m³/s、2757 m³/s和671 m³/s。绘制四水的日最大洪峰流量序列和AM洪峰流量散点图，如图3、图4所示。四水流域的汛期流量整体上均呈现中间高两边低的特点。由图3可知，四水的日最大洪峰序列在6月下旬到8月上旬都呈现出剧烈波动的状态，并在10月中旬后逐渐下降到5000 m³/s以下。由图4可知湘江流域的AM洪峰流量大小主要在5000~20,000 m³/s之间，集中出现在5月下旬到7月上旬，共有25年，自8月起频次明显下降，9、10月各有一年。资江流域的AM洪峰流量量级较小，仅在7、8月有4年超过10,000 m³/s，且在5月中旬到7月下旬的AM洪峰点分布频次变化不明显。沅江流域AM洪峰流量在5、6、7月份分别有14年、21年和20年，占总年数的87%，7月份的AM洪峰流量普遍更高，有9年超过20,000 m³/s。澧水流域5月上旬到6月中旬出现19个AM洪峰流量点，分布密集，但流量大小不超过8000 m³/s；6月下旬到7月下旬流量明显提高，有13年的AM洪水量级超过10,000 m³/s；仅有11年的AM洪峰流量分布于8月到10月。综上所述，各流域汛期中段平均流量最高，前段次之，后段最低，且AM洪峰在8月以前分布更为密集，8月以后的AM洪峰均不超过12个。

综合洪水年内分布和径流分析，可以将流域汛期进行粗略划分，结果如表4所示。

Figure 3. Daily maximum peak flow series of flood season in the Four Rivers basin

图3. 四水流域汛期日最大洪峰流量序列

(a) 1988~2020年湘江(湘潭站) AM洪峰流量散点图 (b) 1951~2020年资江(桃江站) AM洪峰流量散点图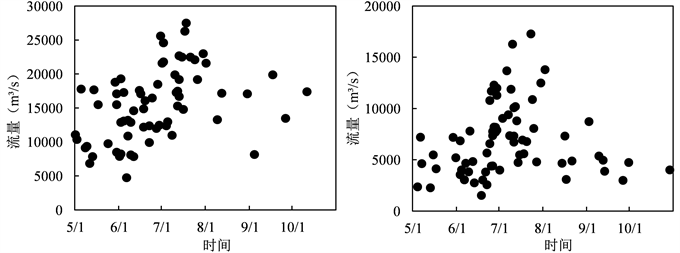(c) 1951~2020年沅江(桃源站) AM洪峰流量散点图 (d) 1950~2020年澧水(石门站) AM洪峰流量散点图

Figure 4. Scatter diagrams of AM peak flows in the Four Rivers basin

图4. 四水流域AM洪峰流量散点图

Table 4. Flood season segmentation based on annual flood distribution and runoff analysis

表4. 基于洪水年内分布和径流分析的汛期分期

4.3. 汛期分期结果分析

采用变点分析法、有序聚类法、信息熵法、圆形分布法、相对频率法等多种分析方法将洞庭湖三支流的汛期分为三期，结果如表5所示。

由表5可知，数理统计方法得到的四水流域汛期划分结果与前文天气成因分析和洪水分布与径流分析的结果范围相近。湘江与资江流域计算结果相近，主汛期时间大致为6月中旬到7月中旬，开始时间相对较早。在沅江和澧水流域，各方法分期结果基本一致。沅江的主汛期大致为6月下旬到7月下旬，澧水的主汛期大致为6月下旬到8月上旬。

Table 5. Flood season segmentation in the Four Rivers basin of Dongting Lake

表5. 洞庭湖四水流域汛期分期计算结果

各流域的均值变点法和概率变点法得到的分期序列都通过了数据的独立性检验，计算的主汛期起止日期基本一致。以沅江流域70年逐日平均流量资料为例，均值变点划分出的主汛期日最大洪峰序列均值为20,126 m³/s，概率变点得到的主汛期超门限值洪水的发生概率为4.80%。分期日最大洪峰流量均值和分期洪水概率大小与多年日平均流量过程线趋势相符，均为“中–高–低”分布。

均值变点法、有序聚类法和信息熵法均通过日最大值取样进行分期计算，仅取样时段长度有所不同。其分期依据离差平方和或信息熵都是对时间序列离散特征的定量描述 [13] [14]，但不能反映出分期洪水的量级和发生概率。湘江的信息熵法、资江流域的有序聚类法和信息熵法得到的主汛期时间与其他方法相差较大，是因为这

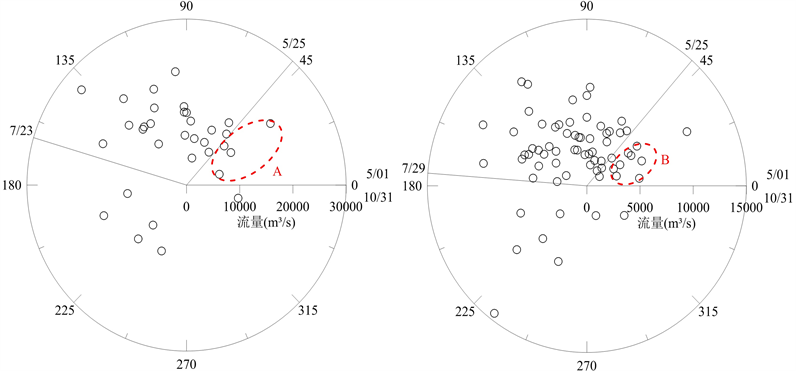(a) 湘江流域(湘潭站)(b) 资江流域(桃江站)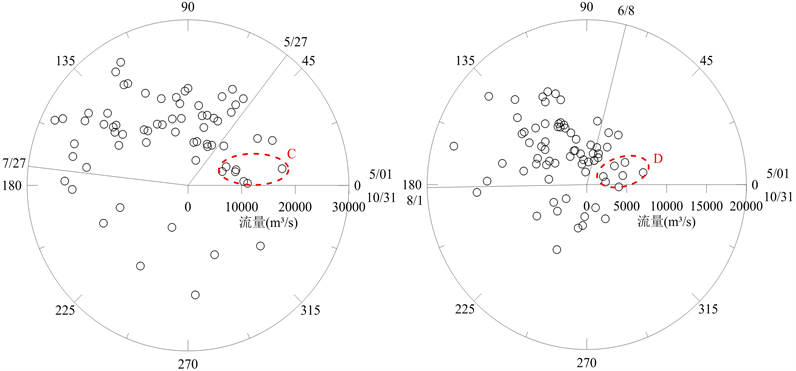(c) 沅江流域(桃源站) (d) 澧水流域(石门站)

Figure 5. Flood season segmentation based on circular distribution method

图5. 基于圆形分布法的汛期分期结果

两种方法仅以整体序列的离散程度最小为原则进行分期，导致主汛期的序列均值反而小于前汛期；以湘江为例，信息熵法所得前汛期5月1日到7月17日的日最大值序列均值为13,088 m³/s，主汛期7月18日到9月4日序列均值为9133 m³/s。而其他方法的主汛期为第二分期，起止时间都在5月上旬到7月中旬范围内，可以更好地描述流域洪水的季节性，对水库分期设计洪水和分期汛限水位的计算更有参考意义。

在圆形分布法中，集中度描述了集中期的集中趋势。本文计算的各流域不同样本时段长度、不同洪水量级条件的集中度范围是0.54~0.65，反映出流域汛期逐日平均流量资料具有一定的季节性。此外，考虑洪水量级的主汛期起始时间内包于不考虑洪水量级的主汛期，说明汛期前期(例如5月上中旬)密集分布且量级较小的洪水会对主汛期的划分具有一定的影响。由于圆形分布法采用AM取样，一旦某年的AM洪峰出现时间较早，导致其得到的主汛期开始时间与其他方法计算结果相比有显著提前，如图5所示。以图5(d)为例，在去掉圆形0˚~40˚ (D区域)的6个AM点同时保持其他点不变的情况下进行分期计算，与原结果对比发现，D区域的6个AM点拉低了整体集中度 $\bar{\alpha }$ 的同时抬高了矢量角度的标准差s，导致主汛期起始日期提前，而结束日期变化不大。与D区域同理，图5的A、B和C区域的AM点也导致了主汛期起始日期提前。但由于后汛期一般持续时间较长，洪水分布稀疏，增删后汛期的AM点对主汛期的起始和结束日期的影响程度相近。

按主汛期取外包的原则，综合各方法结果得到四水流域汛期分期，如表6所示。

Table 6. Flood season segmentation schemes of the Four Rivers basin

表6. 四水流域汛期分期结果

5. 结语

本文从天气成因角度出发，分析了副高活动对洞庭湖降水的影响，综合运用变点分析法、有序聚类法、信息熵法、圆形分布法和相对频率法等多种数理统计方法，对洞庭湖流域的湘江、资江、沅江和澧水水系进行汛期分期研究。本文选取的汛期分期方法兼顾了日最大值取样、AM取样和POT取样等不同的取样方法，发现样本序列不同是各方法分期起止时间产生差异的原因之一。考虑到各个方法不同的取样和优缺点，并结合天气成因、洪水年内分布与径流统计分析，将汛期(5月1日~10月31日)分为前汛期、主汛期和后汛期。四水流域主汛期起止时间分别为湘江6月15日到7月23日，资江6月14日到7月28日，沅江6月20日到8月2日，澧水6月22日到8月9日。

通过多种汛期分期方法比较分析，可以减少主观因素对分期结果造成的影响。本研究仅基于流量序列开展了流域汛期分期研究，考虑到洪水的时间分布受到多种因素影响，未来将结合气候因子、下垫面条件及人类活动要素等输入，开展基于物理成因变量的流域汛期分期研究，以提高汛期分期的可靠性。

基金项目

国家重点研发计划课题(2021YFC3200303)。

参考文献