1. 引言
航空发动机是一个国家军事实力的体现。随着我国航空业的快速发展,对于航空发动机的研究以及航空发动机性能的提升已成为急需解决的关键问题。尾喷管是涡喷发动机的重要组成部分。其主要作用是使发动机燃烧室产生的高温高压气体不断膨胀,将内能转化为动能,为飞行器提供推力。
中心锥作为喷管的重要部件,对喷管出口温度、推力系数、总压恢复系数、流动特性等气动参数起着至关重要的调节作用。因此,针对中心锥开展研究十分必要。2019年杨亚冰等人基于涡扇发动机部件级实时仿真模型,增加了从外涵引气冷却中心锥和尾喷管扩张段内壁的冷却结构和红外预测模块进行仿真,将排气系统后向红外辐射下降了30%以上 [1]。中心锥通过气膜冷却可以大程度降低中心锥表面的温度,有效抑制排气系统的红外辐射 [2]。2002年,刘友宏等用数值模拟的手段,探究了有无中心锥对圆柱混合管热混合效率的影响。分析了圆柱混合管热混合效率在有中心锥时大于没有中心锥时的原因 [3]。2012年,谢翌等采用数值模拟的方法,研究了中心锥关键结构参数对涡扇发动机波瓣混合排气系统气动热力性能的影响规律。当中心锥长度不变时,波瓣混合排气系统总压恢复系数大体上不断减小;排气系统出口处推力系数则呈现出先增大后迅速减小的趋势 [4]。2014年,余斌等对喷管在后半球空间内的红外辐射强度进行了数值模拟,研究了喷管出口形状对于喷管气动性能以及红外辐射强度的影响规律 [5]。2020年,樊开岗等采用SST k-ω模型对微型涡喷发动机进行流场分析,研究了俯仰推力、俯仰推力矢量角与几何偏角之间的线性关系 [6]。
上述研究对中心锥与发动机性能之间的相互关系进行了分析和阐述。本文将进一步探究中心锥对喷管气动性能的影响规律,以140 kg涡喷发动机尾喷管为研究对象,对中心锥结构进行优化,总结中心锥结构的改变对尾喷管气动性能影响的规律。
本文通过构造具有不同中心锥锥角的尾喷管模型,研究不同中心锥几何结构对尾喷管推力以及出口流动状态、总压恢复系数等的影响。通过控制单一变量进行数值模拟研究,凝练中心锥结构的改变对尾喷管气动性能影响规律。
2. 初始喷管气动性能的研究
2.1. 喷管模型
本文选用的发动机为140 kg涡轮喷气发动机。该发动机的三维模型如图1所示。由于该发动机的喷管结构比较简单,因此无需对喷管结构进行简化,相应的参数通过对140 kg涡喷发动机尾喷管逆向建模获得。采用DM建模得到发动机尾喷管模型,发动机尾喷管三维模型如图1所示。该模型是后续数值模拟工作的基础。
2.2. 计算网格
针对本文研究内容,考虑到尾喷管的三维轴对称特征,将计算域简化为图2所示矩形区域,并采用轴对称边界。由于本文主要考虑的是在不同中心锥结构设计下尾喷管的气动性能问题,因此只需要知道喷口截面的压力分布以及轴向速度分布,同时为了避免提取过大的流域,造成计算资源上的浪费,选取计算域尺寸为长度0.5 m,半径0.2 m的矩形区域,该流域可以捕获绝大多数的流动细节,同时也包括了轴线上的流动核心区。
喷管壁面采用等比加密处理,壁面第一层网格厚度为0.0001 m,增长率为1.2。从壁面到外界区域呈由密到疏的趋势。网格划分图如图2所示。
边界层网格如图3所示。
通过对发动机进行实车试验可以测得发动机尾喷管进口的入口气流参数如表1所示:

Table 1. Nozzle inlet airflow parameters
表1. 喷管入口气流参数
2.3. 流场仿真结果分析
本文中采用fluent软件中的k-ε湍流模型进行稳态流场计算 [7]。
根据平台所采集的入口气流参数确定了数值模拟时尾喷口的进口条件,将进口边界条件设为压力进口,入口静压为183,896 Pa,总压为194,282 Pa,入口总温为1100 k;出口边界条件设置为压力出口,静压为101,325 Pa,温度为300 k。求解器设置为密度基,轴线设为轴对称边界。流体设定为理想气体。
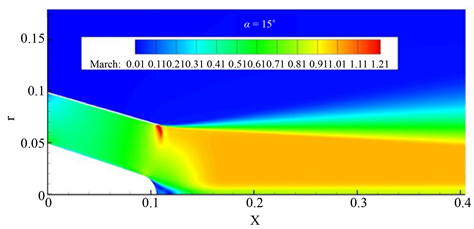
流场仿真分析得到初始喷管三维速度云图、初始喷管轴向速度云图分别如图4所示,图5所示。
由图4和图5对比可知,二维模型与三维模型的流场仿真分析的变化趋势并无明显变化,为了优化操作过程,避免计算资源的浪费,本文后面的分析都采用二维模型。
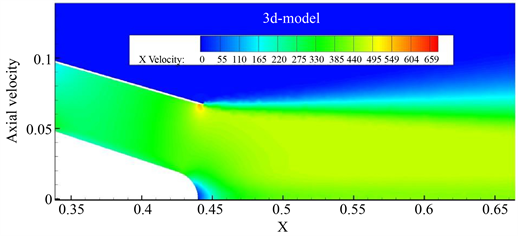
Figure 4. Initial nozzle 3D velocity cloud
图4. 初始喷管三维速度云图
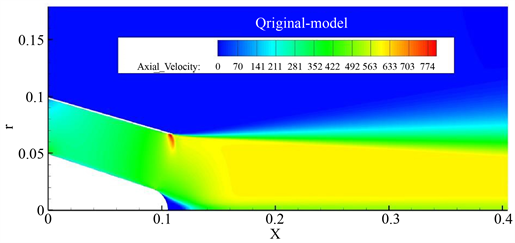
Figure 5. Initial nozzle axial velocity cloud
图5. 初始喷管轴向速度云图
从初始喷管速度图中我们可以明显的看到,初始喷管出口气流速度并不均匀,流速在出口附近产生明显的波动,集中体现在尾喷管出口壁面处和出口中心锥端面处。其中,尾喷管出口壁面处的速度明显变大,而出口中心锥端面处的速度明显减小。初始喷管马赫数云图、总压恢复系数云图分别如图6、图7所示。
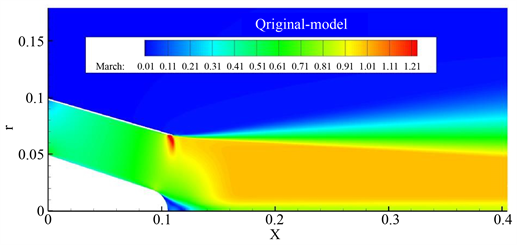
Figure 6. Initial nozzle Mach number cloud map
图6. 初始喷管马赫数云图
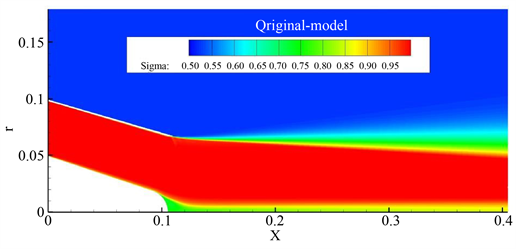
Figure 7. Total pressure recovery coefficient cloud chart
图7. 总压恢复系数云图
从马赫数云图中可以看出喷管出口上壁面处和中心锥尾部分别存在明显的高速区和低速区,尾喷管出口壁面处的高速区马赫数已经接近于1.2,超过了声速,这本不会在收敛喷管中出现,是因为在出口处壁面突然变化,产生了激波,因扰动而造成了此现象。
在图7中,可以清楚地看到喷管主流域的总压恢复已经超过了0.95,但从尾喷管出口的上下壁面开始,都产生了一段很大的总压损失,上壁面及其后端的总压恢复系数在0.63到0.85之间,下壁面及其后端的总压恢复系数在0.82~0.87之间。相比之下,上壁面的总压损失要大一些。
提取出口速度参数如图8所示,可以看出,出口截面的速度分布在起始处R = 0的位置轴向速度为负,之后随着轴向半径R的增大,出口轴向速度的变化趋势是先迅速增加,后缓慢增加,在径向0.06附近时再次迅速增加,到径向约为0.063 m时达到最大,后骤然降低。起始时,速度迅速增加的原因是在中心锥尾端处产生了涡旋,因此出口截面处中心速度为负,而到了径向约为0.063 m的位置时,靠近壁面,已知出口壁面处因扰动产生了激波,因此速度达到最大值后因靠近壁面而导致速度骤然下降。
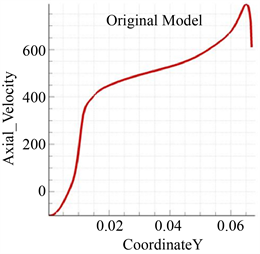
Figure 8. Tail nozzle axial velocity profile
图8. 尾喷口轴向速度曲线
图9为初始喷管流线图,从流线图中可以看出内流域中的气体流动是比较稳定的,而在外流域中,由于内流域中的气流高速流动使得流动区域静压降低,因而外流域的空气产生了流动,由于外流域流动速度较小,因此在速度图中并无明显现象,而流线图则显示的较为明显。
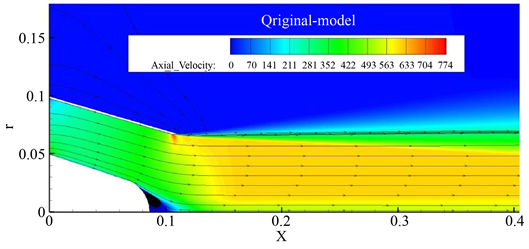
Figure 9. Initial nozzle flow line diagram
图9. 初始喷管流线图
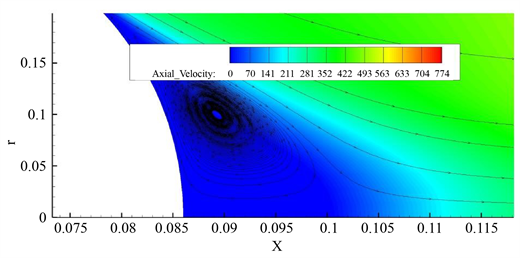
Figure 10. Initial nozzle local flow line diagram
图10. 初始喷管局部流线图
在图10中,在中心锥末端产生了一个回流区,在理想状况下,喷管内的气体是一维定常可压缩管内流动的,而回流区产生的原因是,喷管内的气体在压缩区域内流动时,由于中心锥端面处存在曲率而使气流产生分离。
初始喷管等速线如图11所示,从图中可以看出回流区中心的速度是-60m/s,气流的速度方向不断改变,对出口气流品质产生影响,进而导致喷管性能的下降。
3. 中心锥锥角对尾喷管气动性能影响研究
3.1. 研究内容
前文已经研究了在初始发动机尾喷管结构下的稳态流场特性,得出尾喷管出口上下两端面存在的问题,对我们优化喷管气动性能是十分不利的。因此我们提出修改中心锥锥角对尾喷管气动性能进行研究。期望通过修改中心锥锥角,来达到优化喷管气动性能的目的。
3.2. 前处理设置
建立改变中心锥锥角的二维模型
本次实验的目的是初始喷管中心锥锥角α = 18˚,为避免大幅度改变尾喷管中心锥锥角,导致喷管无法工作,先将中心锥锥角修改为α = 15˚。建立模型进行流场分析。
3.3. 流场仿真结果分析
3.3.1. 中心锥锥角对尾喷管流场压力分布的影响
对修改中心锥锥角的喷管进行流场仿真分析,压力云图如图12所示:
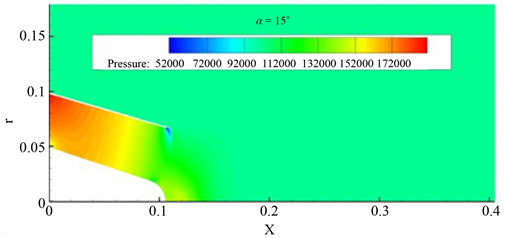 (a)
(a)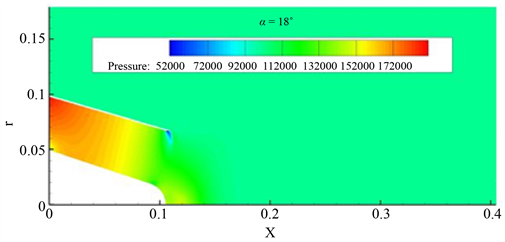 (b)
(b)
Figure 12. (a) α = 15˚ pressure cloud; (b) α = 18˚ pressure cloud
图12. (a) α = 15˚压力云图;(b) α = 18˚压力云图
从图中可以看出,压力从进口到出口呈现明显下降趋势,喷管出口处壁面存在着一个低压区,这是由于喷管出口壁面处存在一个转折,产生激波,发产生了扰动的现象。中心锥端面处的压力较为紊乱,且整体压力较高。对低压区放大进一步分析,画出等压线图,如图13所示。
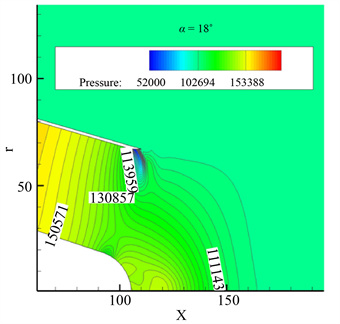
从等压线中可以看出,中心锥端面产生激波处附近的压力也变得很高,流场中高压区与低压区的压力相差约40,000 pa,相当于近0.4个大气压,会严重影响气流流动的稳定性,但从中心锥锥角改变的角度来说,改变3˚对流场的压力分布并没有什么明显的影响。
3.3.2. 中心锥锥角对尾喷管流场速度分布的影响
由于较小幅度的改变中心锥锥角对整个流场区域的压力分布并没有什么明显的影响。所以在简单对比后,下面将对中心锥结构的改变会给尾喷管气动性能带来那些影响开展讨论。喷管轴向速度云图如图14所示:
 (a)
(a) 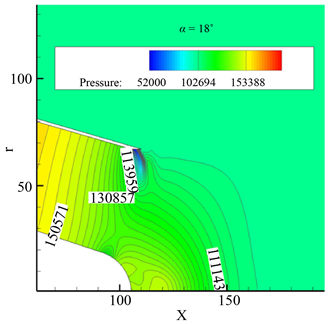 (b)
(b)
Figure 13. (a) α = 15˚ isobaric map; (b) α = 18˚ isobaric map
图13. (a) α = 15˚等压线图;(b) α = 18˚等压线图
 (a)
(a)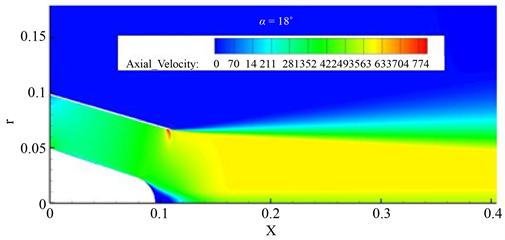 (b)
(b)
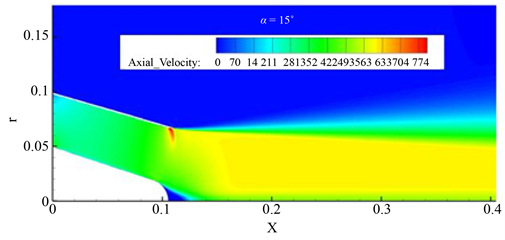
Figure 14. (a) α = 15˚ nozzle axial velocity cloud; (b) α = 18˚ nozzle axial velocity cloud
图14. (a) α = 15˚喷管轴向速度云图;(b) α = 18˚喷管轴向速度云图
从轴向速度图中可以看出,其内流场速度流场分布比较均匀,但是壁面出口处还是存在一个很明显的高速区,为了便于对此处进行分析,放大出口处壁面高速区进行观察,如图15所示。
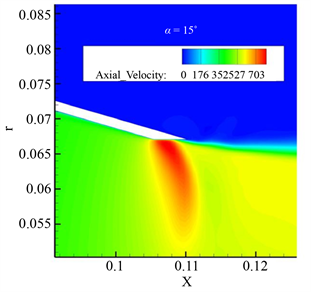 (a)
(a) 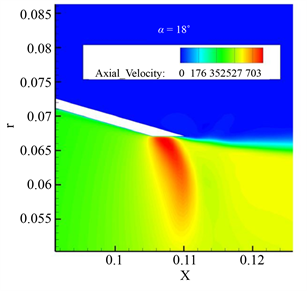 (b)
(b)
Figure 15. (a) Velocity cloud at the exit of α = 15˚ wall; (b) Velocity cloud at the exit of α = 18˚ wall
图15. (a) α = 15˚壁面出口处速度云图;(b) α = 18˚壁面出口处速度云图
从图中可以看出,较小幅度的改变中心锥锥角对整个流场区域的流速并没有什么明显的影响。图16为喷管马赫数云图;图17为总压恢复系数云图。
 (a)
(a) (b)
(b)
Figure 16. (a) α = 15˚ nozzle Mach number cloud diagram; (b) α = 15˚ nozzle Mach number cloud diagram
图16. (a) α = 15˚喷管马赫数云图;(b) α = 18˚喷管马赫数云图
 (a)
(a)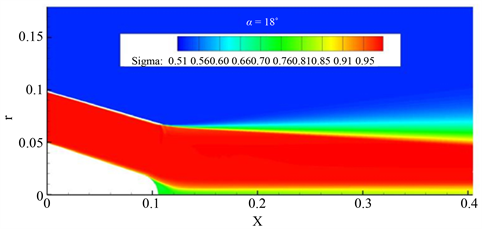 (b)
(b)
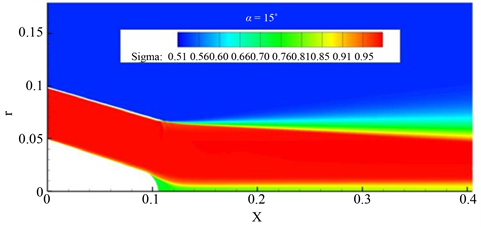
Figure 17. (a) α = 15˚ total pressure recovery coefficient cloud; (b) α = 15˚ total pressure recovery coefficient cloud
图17. (a) α = 15˚总压恢复系数云图;(b) α = 18˚总压恢复系数云图
如图所示,喷管主流域的总压恢复在0.98左右,损失较小,而出口下端出现较大 总压损失,中心锥末端的总压损失是最大的,但比较之下发现,较小角度改变中心锥锥角对尾喷管大多数气动性能的影响并不明显。
提取出口处轴向速度曲线图如图18所示:
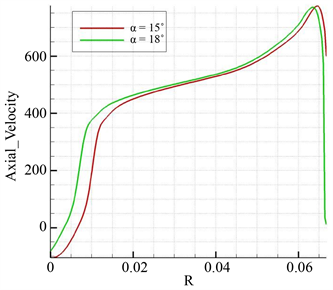
Figure 18. Axial velocity profile at the tail nozzle
图18. 尾喷口处轴向速度曲线图
对比之下,尾喷口轴向速度曲线存在一定差别,α = 18˚尾喷口轴向速度上升较为缓和,在到达壁面附近时,速度达到极值,之后速度快速下降为0;而α = 15˚的尾喷口轴向速度上升较为迅速,坡度比α = 18˚的尾喷管大很多,在速度距离尾喷口还有一小段距离时就会达到极值,达到极值后,尾喷口速度呈缓慢下降的趋势,这是因为中心锥锥角α = 15˚尾喷管回流区域较小导致的。从图中还可以看出,α = 15˚时尾喷口处轴向速度要早一点点到达极值点,这是由于α = 15˚的尾喷管产生的高压区域的范围较大。经计算,α = 15˚的尾喷口轴向平均速度为453.71m/s,α = 18˚的尾喷口轴向平均速度为451.41m/s,α = 15˚的尾喷管平均速度略高一些,速度曲线也平稳很多,在实际工况中,疲劳强度更高,对材料的要求更加宽容,是更优的选择。
4. 总结
本文针对140 kg涡喷发动机尾喷管进行建模,并分析了其不同中心锥结构对尾喷管气动性能的影响。且对初始喷管进行流场仿真,分析了其压力分布以及流场速度分布的情况;通过改变中心锥锥角进行数值模拟,分析了不同结构参数对流场压力分布和速度分布的影响。最终得出了一些如何提高尾喷管气动性能的结论。具体结论如下:
对于改变中心锥锥角对尾喷管气动性能影响的规律性研究中:虽然在中心锥锥角改变较小的情况下,对于尾喷管气动性能的影响较小,但从对尾喷口轴向速度曲线的分析可以得出,当中心锥锥角α在合适范围内降低时,尾喷管出口处的平均速度会升高,速度曲线变得更平稳,在实际工况中,具有更高的疲劳强度。因此,适当降低中心锥的锥角,对尾喷管气动性能的优化是有一定帮助的。
NOTES
*通讯作者。