1. 引言
随着传统电网所需化石能源的逐渐枯竭,大规模分布式电源互联使智能微网已成为大电网的有力补充和有效支撑,而逆变器作为智能微网与电网的接口,向电网注入高质量电能和保障安全运行方面发挥着重要作用 [1]。逆变器有两种控制方式 [2] ,在并网模式下,广泛使用具有良好的动态响应和抗干扰能力的电流控制。孤岛模式下,使用电压控制才能满足供电需求 [3]。但两种模式下输出转换瞬间可能不相等而导致冲击电流、电压尖峰等问题。解决方法是通过电流控制策略来避免电流或电压尖峰 [4] [5] [6] 研究电流控制策略来避免电流或电压尖峰。而分布式发电技术的引入,解决了许多智能微网互联中的脉宽波形波动、功率开关不稳定、电源开关死区时间和电压谐波等潜在问题。因此基于逆变器的分布式发电在供电安全、电压质量和电力系统稳定性方面达到期望的动态控制特性和实时调节的效果 [7]。
分布式发电基于逆变器结构及不同控制策略,解决不同运行模式下故障诊断、转移等问题,实现电网稳定和高质量电能 [8]。而逆变器建模在智能微网中对提高系统性能、稳定性、弹性和可靠性具有重要作用 [9]。当以新能源为主的分布式发电大规模并入电网后会产生复杂的渗透,为了使系统能够较全面的符合要求运行,智能微网需采用不同的辅助控制策略来解决供需电能不匹配、电压波动、频率波动、电压谐波、频率波动、输出功率不稳定等问题 [10]。在2011年自动化会议上,提出智能微网通过静态转换开关与公用电网相连,连接点称为公共耦合点。使用大电网的频率和电压作为调节依据,通过二次控制调节逆变器的有功和无功功率。用功率因数来调节有功和无功功率。但是该控制方法接入电网,智能微网就会失去对系统的频率和电压的控制等问题,从而导致电能质量降低。因此,众多国内外学者对逆变器技术展开了更加深入的相关研究并通过不同的控制策略来维持电网稳定,输出高质量的电能。文献 [11] 提出一种混合控制方法以了解系统的动态行为;文献 [12] 提出零输出阻抗电流下垂控制方法;文献 [13] 提出逆变器并联模型与改进的控制技术,抑制系统中的环流并使负载功率可任意均分。为了验证并离网切换过程中的需求,文献 [14] 分析逆变器的可靠性与故障类型,增强系统稳定性;文献 [4] 提出硬件结构不变,改变开关频率提高三相并网逆变器输出功率质量和效率的控制策略;文献 [5] 提出降低开关频率的模型预测功率控制方法消除逆变器谐波失真;文献 [15] 提出孤岛检测方法保证系统改进后的稳定性和准确性;文献 [16] 采用自适应补偿方法;文献 [17] 实现多能源整合时保证电能质量的高效性和可靠的稳压特性;文献 [18] 提出一种具有自动开关延时的虚拟同步发电机无差调频控制策略;文献 [19] 改善虚拟同步发电机控制逆变器的阻尼特性设计;文献 [20] 提出了一种基于虚拟阻抗的柔性功率调控策略,以改善功率分配精度;文献 [21] 提出级联H桥逆变器驱动永磁同步电机的鲁棒预测电流控制策略解决参数敏感和矢量选择繁琐问题;文献 [22] 在节约成本和系统空间基础上提出其控制策略,进行功率的实时跟踪、增强可靠性。
本文综述了对逆变器实施不同的控制策略以达到输出高质量电能的目的。根据上述文献逆变器技术的研究现状可知,基于逆变器控制技术除了稳定电压、频率等波动外,它在抑制谐波、功率因数校正等方面都有着显著的效果。为进一步了解当前改善电能质量技术的发展状况,本文通过对相关文献的分析,归纳逆变器控制策略对系统稳定性、电能质量等方面的探究。最后对其研究方向、技术发展进行了展望。
2. 逆变器原理
开发逆变器模型之前,保证逆变器母线电压恒定防止过载事件期间崩溃,主要用于检查相对小的扰动下的系统动态稳定性。逆变器内部电压
的幅值
和相角
通过等效电路计算三相输出电流的基准值模型 [23]:
(1)
其中:
、
是逆变控制器输入三相端电压和电流,
、
是逆变器内部电流和导纳。
如图1建立典型的智能微网系统,提出典型大信号非线性动力学模型,并通过功率、电压和电流控制器调整逆变器电桥的输出电压和频率,其参考坐标系中表示的动力学方程模型如下 [24]:
(2)
其中状态向量是:
,
是已知干扰,
、
、
是状态表达式。一次控制保持智能微网的电压和频率稳定性 [25]。
随着电力系统控制越来越复杂化,再也不能继续以往单一控制方式,其缺点随着研究与开发逐渐凸显,响应速率慢、谐波分量较大。因此,需要开发并选择不同结构的逆变器也成为了当前研究的热点。
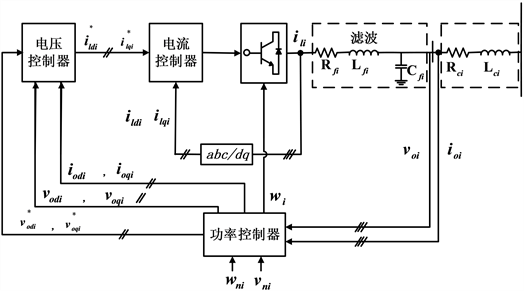
Figure 1. Intelligent microgrid block diagram based on inverter
图1. 基于逆变器的智能微网框图
3. 逆变器结构及其拓扑
逆变器是连接到转换器输出并将直流电源转换为交流电源的设备,可将直流电源转换为交流电源。将输出功率反馈给交流负载之前对其进行整形。本节讨论了逆变器的主要分类。
3.1. 常规逆变器拓扑
传统带升压变换器拓扑结构为无变压器逆变器,在这种传统设计中如图2,由升压变换器和全桥逆变器组成。为提高升压变换器双桥逆变器的效率,设计了滞环电流控制模型,并改善直流电压的拾取。
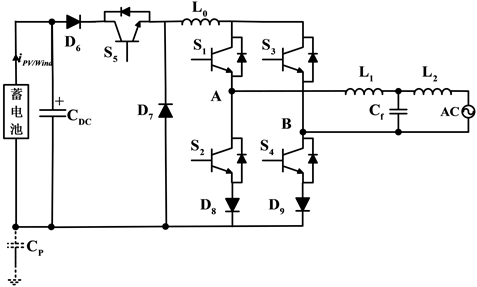
Figure 2. Conventional full bridge inverter
图2. 常规全桥逆变器
如图3将全桥改变为半桥且并联两个电容消除电桥单独设置的需要,实现低电压叠加和电能转换效率。如图4将升降压变换器与光伏板等输出端口反并联构成新的逆变器模型解决升压逆变器的较差问题。

Figure 4. Dual source anti parallel step-up and step-down inverter
图4. 双源反并联升降压逆变器
仅考虑开关计数限制逆变器的使用,使用LC阻抗网络改进传统H桥逆变器。如图5具有连续电压增益的Z源逆变器对单相实现更为可取。如图6反激式逆变器拓扑结构采用电感器与变压器相结合弥补直流逆变器需求,实现高性能、长寿命和低制造成本 [26]。
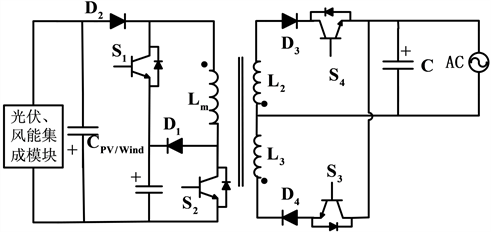
Figure 6. Three port fly-back inverter of coupling circuit
图6. 耦合电路的三端口反激逆变器
由于反激式逆变器具有高电磁干扰,效率低,尺寸和重量增加的缺点。如图7功率逆变器克服了上述逆变器的开关损耗、频率低、谐波等问题,实现整流正弦波。并总结出如表1的常规逆变器结构优缺点。
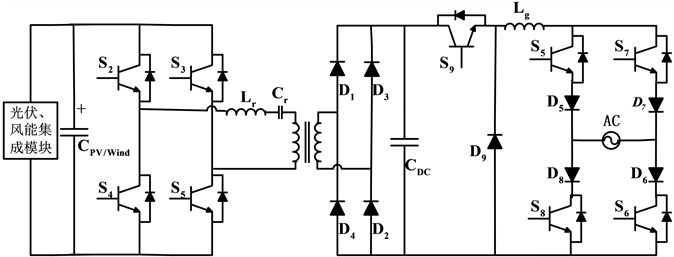
Figure 7. Three stage fly-back inverter with soft switch
图7. 具有软开关的三级反激逆变器

Table 1. Advantages and disadvantages of various conventional topologies
表1. 各种常规拓扑结构的优缺点
3.2. 新型逆变器拓扑
分布式能源的并入增加了电网复杂的渗透能力,以单电平为主的逆变器结构不能满足多输入多输出的用户需求。因此多电平逆变器(Multilevel level inverter, MLI)在研究和工业中受到越来越多的关注,不仅产生更高的电压水平,还可降低无源滤波器要求。许多行业将MLI拓扑当做是一种经济高效的解决方案,根据配置结构和输出电压由直流电源和半导体器件组成。此外还消除了原始二极管箝位MLI的缺点 [27]。
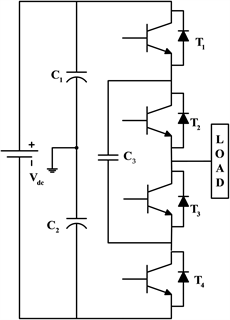
但如图8传统MLI需要更多组件计数扩展级别数。对驱动电路、散热器和保护电路的要求增加。导致系统规模增加、控制方案复杂、系统成本增加 [28]。为克服这些问题,引入减少元件数拓扑,分为对称、非对称和混合配置三大类。
 (a)
(a) 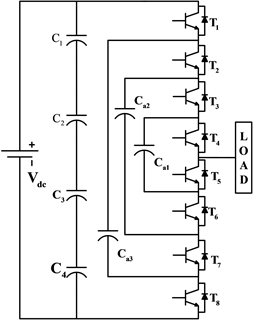 (b)
(b)  (c)
(c)
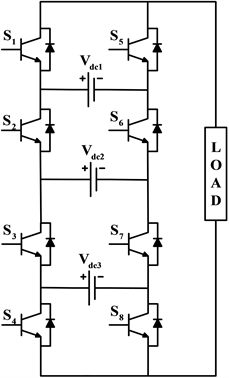
Figure 8. Traditional multilevel inverter topology. (a) Three level; (b) Traditional five level; (c) Cascade H-bridge five level
图8. 传统多电平逆变器拓扑。(a) 三电平;(b) 传统五电平;(c) 级联H桥五电平
对称多电平逆变器在这一类中,最近开发的大多数对称多电平拓扑都是单相的。并且基本上简化开关MLI拓扑分为两组,例如图9不带H桥MLI和图10带H桥MLI。
 (a)
(a) 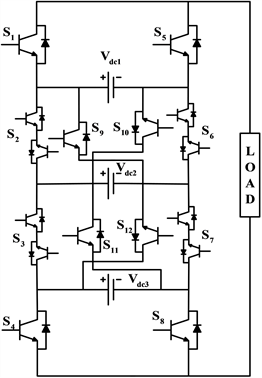 (b)
(b)
Figure 9. Simplified switched symmetric MLI topology without H-bridge
图9. 无H桥简化开关对称MLI拓扑
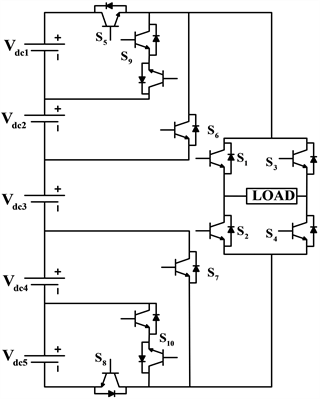 (a)
(a) 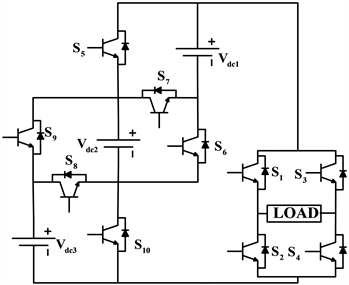 (b)
(b)
Figure 10. Simplified symmetric MLI topology with H-bridge
图10. 具有H桥简化对称MLI拓扑
不对称MLI如图11的直流电源的电压幅值不同。与对称MLI相比,非对称MLI主要目的是以相同数量的元件产生更高数量输出电压电平。主要因素是输入直流电压幅值的选择。其各种拓扑分为以下几类。
1) 在不改变拓扑结构的情况下,放置非对称直流电源而不是对称直流电源。
2) 将由两个或三个直流电源组成的对称形式的基本单元进行扩展,然后在不同的不对称条件下将所开发的基本单元串联起来。
3) 以由两个或三个直流电源组成的不对称形式扩展基本单元,然后将开发的基本单元串联。
而如图12混合MLI是提高输出波形质量和增强性能参数的另一种方法。通过使用两种拓扑的组合生成。许多拓扑是通过直流电压比例关系的可控自由度生成的。且任意两种简化开关拓扑的组合,以及简化开关MLI与传统MLI组合以及所有MLI拓扑均在对称和非对称条件下讨论,H桥类别称为混合MLI。
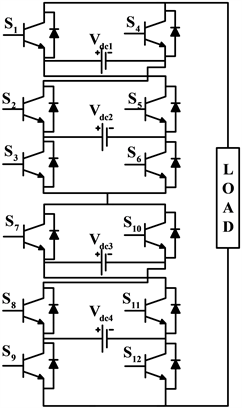 (a)
(a)  (b)
(b)
Figure 11. Simplified switch number asymmetric MLI topology with H-bridge. (a) Without H-bridge; (b) With H-bridge
图11. 具有H桥简化开关数不对称MLI拓扑。(a) 无H桥;(b) 具有H桥
4. 逆变器下的控制策略及分析
采用可行的控制策略控制智能微网中逆变器,对提高系统性能、稳定性、弹性和可靠性具有重要作用。为得到高质量电能,智能微网采用不同控制策略操作逆变器,使系统能够较全面地符合要求运行。
4.1. 基于电压和频率控制
该控制方法主要用于传统电网运行,基于逆变器控制频率不稳定和电压偏差以改善负载变化等影响。其中动力学方程及设计框图如下 [29]:
(3)
其中:
、
是PI控制器定义的辅助状态变量,
是标称角频率;
、
为PI控制器定义的辅助状态变量,
、
是直分量
的正交分量,其设计框图如图13。
 (a)
(a) 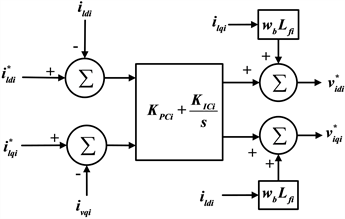 (b)
(b)
Figure 13. Block diagram of voltage and current controller. (a) Voltage control; (b) Current control
图13. 电压、电流控制器的框图。(a) 电压控制;(b) 电流控制
为保证电能输出,加快响应就会降低稳定性、出现谐波问题。文献 [9] 提出
重复控制策略降低电压控制器的复杂度且响应快,提高电能输出稳定性。通过介绍PI双闭环控制有效抑制电网谐波问题,降低电网阻抗对电网电能质量的影响实现电压稳定 [30]。为改进传统控制器设计,提出谐波条件下的智能微网逆变器动态向量控制方程及图14的设计框图如下 [31]:
(4)
其中:下标h表示h次谐波分量,下标j表示
或
框架上的电流。
缺点是单一的改善了电压谐波影响,为进一步解决线路阻抗不匹配和非线性负载等问题。通过结合其他控制方法来解决这些问题。

Figure 14. Proportional resonant voltage controller
图14. 比例谐振电压控制器
4.2. 基于有功和无功功率控制
智能微网中负荷波动、频率和电压扰动可不遵循电压–频率控制策略 [32]。通过逆变器向电网注的有功功率和无功功率控制发电机输出电压和电流,实现高质量电能需求 [33]。功率控制器微分方程可以写成:
(5)
其中:
、
、
、
是的直分量
、
的正交分量,参考电压
和
,工作频率
,截止频率为
,输出有功功率和无功功率的基波分量分别为
和
。并建立如图15的设计框图:
在解决功率控制下频率问题的同时,通过模型预测功率控制方法使开关频率较低,瞬态响应速度较快 [5]。也采用功率估计和设定来调制逆变器,克服传统控制器频率下降的缺点 [4]。根据以下模型状态方程和设计框图16,利用无功功率管理进行频率控制,减少在突发事件期间智能微网频率的下降 [34]。
(6)
其中:参考值*、有功下垂增益
,有功功率、频率和电压标称值
、
、
。
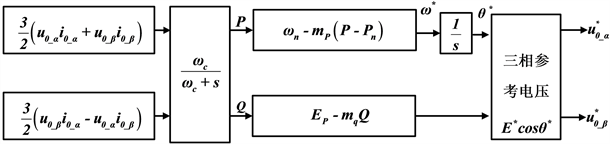
Figure 16. Power controller under low-pass filtering
图16. 低通滤波下的功率控制器
同样该控制策略忽视了功率分配平衡,基于虚拟阻抗的柔性功率调控策略来改善并联系统的功率分配精度 [20]。为进一步实现分布式发电系统稳定和高质量发电,延伸出下垂控制方式改善阻抗、阻尼、惯量变化的影响。
4.3. 基于下垂控制
根据智能微网逆变器输出的有功和频率、无功和电压之间分别存在的线性关系,调节其频率、电压在合理范围内波动,间接实现有功和无功功率的控制目的。而下垂控制方式基本运行在孤岛模式下,通过调整输出功率来满足负载所需保证电能质量 [10]。为改善传统下垂控制克服线路阻抗不匹配问题,设计了增强型限流下垂控制器保证电网故障下的稳定性和最大功率注入,实现并联逆变器之间的无功功率分配 [17]。且基于虚拟阻抗的下垂控制改善并联逆变器之间的无功功率分配 [35]。为解决电压调节退化这一问题,从而提出自适应压降控制逆变器用于解决缓慢的瞬态响应,保证电压和频率在可接受的范围内实现逆变器之间功率分配 [33]。同样针对非线性负载的情况,引入了频率自适应、阻尼补偿等机制来应对电网频率变化。
4.4. 其他控制策略
在智能微网运行中,扰动使频率和电压调节能力下降造成系统输出不稳定,而必要的阻尼等补偿措施克服扰动带来的影响并保证电能质量。加入以系统频率、虚拟阻抗为自适应控制变量的阻尼补偿模块增大阻尼 [16]。而传统逆变器缺乏足够的机械惯性和系统阻尼,采用虚拟同步发电机补偿方法控制转子惯量增大机械惯性 [36]。但依赖于系数调节,逆变器很难在扰动情况下为系统提供惯性与阻尼支撑,导致微电网易失去稳定。虽然增大阻尼会解决振荡问题使系统稳定 [37] ,但没有考虑到阻尼变化带来谐波的影响。为了解决这一问题,采用完全电压前馈策略降低入网电流的总谐波失真以提升并网功率因数 [21]。也通过PI控制器新算法控制无功功率和输出电压的大小避免并网电压波动太大、减小电网冲击、提高系统的稳定性 [2]。同样提出虚拟同步发电机无差调频控制策略,实现智能微网频率恢复和功率按比例分配,有利于系统稳定性的提高 [18]。
尽管对逆变器有多种控制策略,实现了系统的稳定性。但在解决对逆变器欠阻尼、低惯量的问题时,对系统电感增大所产生的等效负阻尼问题研究较少,电能质量问题凸显。通过虚拟阻抗法补偿线路电感的负阻尼,增大系统的阻性成分,提高系统的电能质量输出 [19]。文献 [21] 采用级联H桥逆变器驱动降低永磁同步电机的双矢量鲁棒模型预测电流控制策略以提高鲁棒性。而基于虚拟阻抗的柔性功率调控策略,改善功率分配精度,提高系统鲁棒稳定性和电能质量 [20]。也提出一种与PQ间接电流控制技术相结合的改进型无电压传感器控制策略,提高系统可靠性并改善电能质量 [38]。
5. 总结与展望
本文分析了智能微网逆变器基本工作原理并归纳不同级逆变器拓扑结构及相关控制策略。并根据相关文献对出现的缺点依次提出了解决措施。与传统的逆变器相比,逆变器的高渗透率可以提高孤岛配电系统的电压和频率稳定性;它的发展打破了发电侧发电电量跟随需求侧用电电量的传统模式,节省电能的同时,也解决了许多电网中出现的电能质量问题(如:抑制谐波、调节频率等)。随着科研人员对逆变器技术的不断深入研究,逐步解决了尚还存在的不足之处并对逆变器进行了展望:
1) 提出新或改进逆变器拓扑结构,能进一步提高控制精度,减小逆变器输出电压的谐波。保证非关键负载能在允许的电压波动范围内正常工作,若有必要可用其它调压措施来调整。
2) 虽然这些控制策略对性能进行了改进,满足逆变器的稳定性问题,提高智能微网的增益。但依旧面临着:如低系统惯性、低电抗电阻比、可再生能源的不确定性和间歇性等严峻的挑战。
3) 考虑到更小的尺寸、更低的惯性、电力电子接口分布式发电的参与以及需求峰值的有限平滑转换。设计逆变器具备远程监控功能和系统运行、报警、可编程逻辑控制器设定点等功能。当出现问题时,可以作出更快、更准确、更智能切断需求以减小运行负载损失。并且提供数字继电器、提供数字通信、自适应保护、超快速(子周期)保护等保护及维护措施,尽量减少电力系统设备的损坏。
4) 具有高能量密度、长循环寿命、低维护要求的逆变器储能技术,在提供电压和频率支持、功率分享、调峰等功能的同时,还保证系统的可靠性、弹性、快速瞬态扰动控制以提高电能质量。
5) 逆变器技术的改进促进越来越多的智能微网项目,使农村环境得以改善;由于智能微网的传输损耗低、大型电网中的网络安全问题以及研究机构等部门对安全可靠的供电选择需求,保证了供电安全。