炼钢厂噪声特性分析

Analysis of Characteristics of Noise in Steelmaking Factory

摘要: 为了准确地描述炼钢厂噪声特性，采用专业传声器数据采集系统和VA-Lab2软件对炼钢厂典型冶金设备的噪声进行测量，应用自主开发软件分析炼钢厂不同设备的噪声频谱、总声级、盒计数维数、变分维数和信息维数，并给出炼钢厂噪声和乐器乐声的区别。结果表明，在A计权声级下，转炉、LF炉、RH炉的噪声倍频程变化规律相似，古筝、江南丝竹和手鼓的乐声倍频程变化规律相似，且乐器的倍频程高于炼钢设备的倍频。转炉、钢包炉、RH炉的噪声盒计数维数约为1.01，变分维数约为1.31，信息维数约为4.1。声音时域信号的分形维数(盒计数维数和变分维数)能区分炼钢厂噪声和乐声，而声音频域信号的信息维数则无法区分炼钢厂噪声和乐声。

Abstract: In order to describe the characteristics of the noise in a steel-making plant accurately, the noise of the typical metallurgical reactors in a steel-making plant was measured by the professional microphone data acquisition system and VA-Lab2 software, and the noise spectrum, total sound level, box-counting dimension, variational dimension and information dimension of different metallurgical reactors in steel plant were analyzed by home-made source codes. The results show that, on the base of A-weighted sound level, convector, RH furnace and ladle furnace have a similar rule on the sound octave, Guzheng, Jiangnan traditional stringed and woodwind instruments and tabor have a similar rule on the sound octave, and the sound octave of musical instruments is greater than that of metallurgical reactors. The noise box dimension converter, ladle furnace and RH furnace are 1.01, the variational dimension is 1.31, and the information dimension is 4.1. The fractal dimension (box-counting dimension and variational dimension) of the sound signal in the time domain can differentiate between the noise in the steelmaking plant and the music, but the information dimension of the sound frequency domain signal can’t differentiate between the noise in the steelmaking plant and the music.

1. 引言

人类面对的环境污染主要包括水污染、废弃物污染、大气污染和噪声污染。噪声是一种特殊的环境污染。它没有表面的污染产物，对环境的不利影响不存在积累效应，而且传播的距离也有限 [1]。目前，科研工作者往往专注于其它三种污染，而对噪声污染研究较少 [2]。事实上，在特定场合，噪声对人员也存在很大的伤害。传统噪声会影响人员的工作注意力，从而降低工作效率；但是高强度噪声会对人员的听力产生损害，影响工作人员的身心健康。这样的现象在传统钢铁企业中表现尤其明显 [3] [4]。目前，高校与钢铁公司科研人员联合开展了废水、废渣和废气的无害排放、综合利用等基础和应用性研究，经济性和社会性效益显著，但是噪声问题长期处于忽略的状态。

主观评估和客观参数评估是对声音进行评估的两种常用方法 [1] - [9]。主观评估是利用专业人员的听觉来分析声音的特点(节奏、力度、音调和音程等)。主观评估的结果有5个级别。1) 级别优要求声音不存在失真现象；2) 级别良的标志是声音略显失真，给人的感受是不讨厌；3) 级别中的标志是声音存在明显失真现象，给人的感受是略为厌恶；4) 级别差的标志是虽然声音不令人反感，但是人员出现讨厌的感受；5) 级别劣的标志是此声音的感受令人反感，十分厌恶。主观评估要给出一个准确的结果需要大量的参与人员，因此，工作量十分巨大。客观参数评估则相对简单。首先，此方法需要利用专业的声音采集设备记录声音的时域信号；然后，根据音频信号的声压级、频率、功率谱密度、信噪比、分形维数、失真程度等来定量描述声音的特性。因此，客观参数评估法具有良好的重现性。

声音在时域和频域的波形特征可以表征声音的特性 [9] - [13]。其中，时域波形表征了声音的声压随时间的变化关系；频域波形则表征了声音声压幅值与频率的对应关系。声音信号在时域和频域均表现出大小周期的准周期性，表现出较明显的整体与局部的相似性。为了更好地刻画声音的特征，本文引入分形理论试图量化乐声和炼钢厂冶炼设备噪声之间的差异。

1984年，周浩庆 [14] 首次报道了钢铁企业炼铁、炼钢、轧钢等生产单位的声压级，引入了钢铁厂噪声主动控制的技术思想。2003年，Mizoue [15] 最先分析了日本钢铁厂男性工人吸烟、噪声频率、年龄、听力受损之间的关系，为钢铁厂噪声评价奠定了基础。本文利用专用音频数据采集设备采集并记录炼钢厂主要冶金设备(转炉、LF炉和RH炉)的有效噪声信号；接着利用VA-Lab2软件的数据分析模块以文本形式导出所需噪声的时域数据，最后采用基于Fortran语言开发的自主产权软件Noise Analysis 1.0分析炼钢厂冶金设备工作噪声的特点。为了更加明确地表征炼钢厂的噪声特点，古筝乐曲(山不转水转)、江南丝竹乐曲(夜行船)和手鼓乐曲(乌兰巴托的夜)被选为对比样本。本文涉及的具体分析方法如下：首先利用快速傅立叶变换得到声信号的频谱，然后引进电磁信号的盒维数方法和变分估计方法获取声音时域信号的分形维数，最后利用电磁信号的信息维数的计算方法得到声音频域信号的信息维数。

2. 噪声分析方法

2.1. 采样

声音的声压和频率直接影响人耳对声音的感觉。通常情况下，人的听力对声音的高频部分感觉比较灵敏，而对声音的低频部分感觉比较迟钝。为了更好地反映声强感知的响应特性，本研究在开始数据采集前，利用CA111校准器标定音频信号采集设备；然后利用MP201型传声装置、MA231型前置放大装置和MC3022型二进二出数据采集装置对音频信号进行采样和记录。

2.2. 时域信号

虽然豪斯道夫维数在分析经典的简单分形图形中发挥了重要作用，但是它难以处理具体分形对象。因此，实际的分形研究往往采用盒维数、信息维数和变分估计维数等来进行评估分形维数。

2.2.1. A计权声压级

因为1/1倍频程结果简单实用，能够准确地评估炼钢厂噪声对人的听力的影响。因此将采用音频数据采集设备得到的声压级数据，转化为1/1倍频程A计权声压级数据 [8] [16] [17]。这个数据转换分为两个步骤。

1) 基于参考声压p_ref，利用声压级数据计算序号为i的中心频率声压级L_i。

$L_i=20\lg \frac{{\displaystyle \underset{j=1}{\overset{m}{\sum }}{p}_{ij}}}{p_{\text{ref}}}$ (1)

式中，m是序号为i的中心频率区域内频率的数目。p_ij是序号为i的中心频率区域内序号为j的频率的声压，Pa。

2) 基于序号为i的中心频率声压级L_i评估A计权总声压级L'。

$L^{\prime }=10\lg \left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{10}^{\frac{A+L_i}{10}}}\right)$ (2)

式中，n是中心频率的个数。

2.2.2. 盒维数

如果声音的时域声压信号为p_i， $i=1,2,\cdots ,n$，那么声音时域信号的盒维数D_b [18] 可采用下式计算。

${\delta }_1={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|p_i-p_{i+1}\right|}$ (3)

${\delta }_2={\displaystyle \underset{i=1}{\overset{n/2}{\sum }}\left[\max \left(p_{2i-1},p_{2i},p_{2i+1}\right)-\min \left(p_{2i-1},p_{2i},p_{2i+1}\right)\right]}$ (4)

$D_b=1+{\log }_2\frac{{\delta }_1}{{\delta }_2}$ (5)

2.2.3. 变分估计分形维数

变分估计方法是分析股票市场波动规律的有效工具 [8] [19] [20]。注意到股票价格的波动和声音声压的波动具有相同的数学表达，因此变分估计方法可以被引入声学领域用于分析声音的特性。在时间定义域[t₁, t₂]内，对于长度为的子时间区域，声压p的振幅可表示为：

$OS{C}_{\epsilon }\left(p,\tau \right)=\left|\underset{\left|\tau -t\right|<\epsilon }{\max }\left(p\left(t\right)\right)-\underset{\left|\tau -t\right|<\epsilon }{\min }\left(p\left(t\right)\right)\right|$ (6)

在此基础上，采用子区域长度ε作为时间度量尺度，声压p在定义域[t₁, t₂]的平均振幅可采用下式计算。

$VA{R}_{\epsilon }\left(p,t_1,t_2\right)=\frac{1}{t_2-t_1}{\displaystyle {\int }_{t_1}^{t_2}OS{C}_{\epsilon }\left(p,\tau \right)\text{d}\tau }$ (7)

这样，变分估计的分形维数可表示为：

$D_V=\underset{\epsilon \to 0}{\lim }\left(2-\frac{\lg VA{R}_{\epsilon }\left(f,t_1,t_2\right)}{\lg \epsilon }\right)$ (8)

2.3. 频域信号

如果声音时域信号经过傅里叶变换后的频域信号集合可以用 $\left\{F_i,i=1,2,\cdots ,M\right\}$ 表示。 $\left\{A_j,j=1,2,\cdots ,N\right\}$ 是F集合的一个有限 $\epsilon$ 覆盖，那么集合F的元素出现集合 $A_j$ 的概率 $P_j$ 可定义为：

$P_j=\frac{N{\left(F\right)}_j}{N\left(F\cap A_j\right)}j=1,2,\cdots ,N$ (9)

式中，N是元素的个数。

因此，声音频域信号的信息熵可表示为：

$S_I={\displaystyle \underset{j=1}{\overset{N}{\sum }}{P}_j\lg \frac{1}{P_j}}$ (10)

声音频域信号的信息维数 [21] [22] [23] 可采用下式计算。

$D_I=\underset{\epsilon \to 0}{\lim }\frac{S_I\left(\epsilon \right)}{\lg \epsilon }$ (11)

3. 炼钢厂噪音采集及特性分析

3.1. 炼钢设备的时域特征

图1给出不同声音信号的声压随时间变化规律。转炉、RH炉和LF炉的噪声呈现出振幅为0.5 Pa的疏密相间的振荡；同时声压的强扰动也会随机地出现，其幅值有时高达2 Pa。总体而言，炼钢设备声音的时域图特征是杂乱无章、无明显规律，炼钢设备声压振幅从大到小的次序是转炉、RH炉和电炉。

图1表明，古筝(山不转水转)和江南丝竹(夜行船)的时域图出现了明显的力度强弱变换和节奏的跃迁。其中，江南丝竹的时域信号的声压振幅从2 Pa跃迁到16 Pa，强弱切换的时间量级为0.1秒；古筝的时域图呈类纺锤形，声压振幅从2 Pa跃迁到8 Pa，强弱切换的时间量级为0.1秒；手鼓(乌兰巴托的夜)的时域图基本为等幅振荡，声压振幅约为6 Pa。

综上，炼钢厂噪音的时域图和音乐的时域信号有明显的差异。炼钢厂噪音的特点是强扰动的随机出现，振幅的变换特性是随机且无节奏。从整体上看，音乐时域信号可能出现等幅振荡，也可能出现纺锤形振荡，强弱切换的时间量级为0.1秒。

(a) 转炉；(b) RH炉；(c) LF炉；(d) 古筝；(e) 江南丝竹；(f) 手鼓

Figure 1. Time-domain signal of sound in steel-making equipments and musical instrument

图1. 炼钢设备和乐器的声音时域图

3.2. 炼钢设备的频谱特征

图2给出了不同炼钢设备噪声的频谱。从整体趋势上看，转炉、RH炉和LF的声压幅值随着频率的增加呈现增加→减小→波动→稳定的变化趋势，声压的幅值的变化范围大致为−30 dB至50 dB；而且转炉、RH和LF炉的噪声频谱特点十分相近。当频率在2000 Hz附近时，频域信号存在一个明显的波峰；当频率约为3200 Hz时，出现了声压幅值极小值。转炉的噪声声压幅值在4000 Hz附近时存在一个极大值，然后随着频率的增加，声压幅值在总体上出现缓慢减小的趋势。当噪声频率大于11,000 Hz时，转炉和RH炉的声压幅值振荡幅度基本保持不变，而LF炉约在4500 Hz以后声压幅值振荡幅度基本保持不变。然而，乐器音乐的声压幅值在总体上呈现随着频率的增加基本维持不变的均势，其幅值范围集中在20 dB至50 dB之间。

图3表明不同炼钢设备(转炉、LF炉、RH炉)噪声在A计权下声压的倍频程变化规律相似。炼钢设备噪声的倍频程随着频率的增加先增加后降低；当频率为4000 Hz时，倍频程达到最大值102 dB。这是因为声音的产生机制存在巨大差异。转炉冶炼钢液需要使用氧枪进行超音速顶吹，采用氮气进行底吹，转炉冶炼的噪音的本质是空气动力学噪声；真空精炼反应器RH的噪声是由附属的抽真空设备所产生，属于机械噪声；LF精炼钢液则需要电极进行埋弧操作，LF精炼噪声是由石墨电极电弧产生，属于电磁噪声。在炼钢环境中，冶金人员的感受是烦躁，冶金设备噪声具有音量大、不同频率的音高和音强变化十分混乱。

图3还表明乐器(古筝、江南丝竹和手鼓)乐声在A计权下声压的倍频程的变化规律相似；乐器乐声的倍频程高于炼钢设备噪声。乐器乐声的倍频程随着频率的增加呈现总体上逐渐增加的趋势，但在4000 Hz以后基本保持不变。古筝属于弹拨乐器，手鼓属于打击乐器，而江南丝竹由琵琶、二胡、三弦、秦琴、扬琴、箫、笛等乐器构成，乐器音乐的主要特点是清新悦耳、不同频率音高和音强变化平缓等。

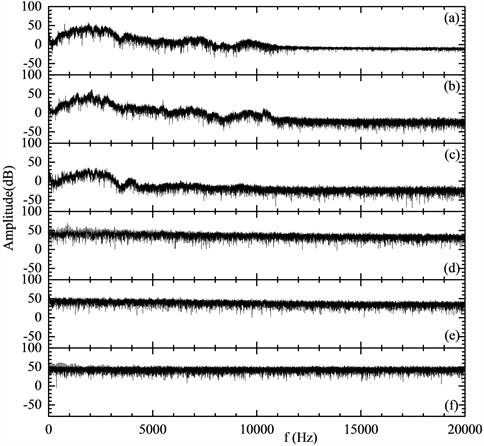(a) 转炉；(b) RH炉；(c) LF炉；(d) 古筝；(e) 江南丝竹；(f) 手鼓

Figure 2. Noise spectrum of steel-making equipments and musical instrument

图2. 炼钢设备和乐器的频谱图

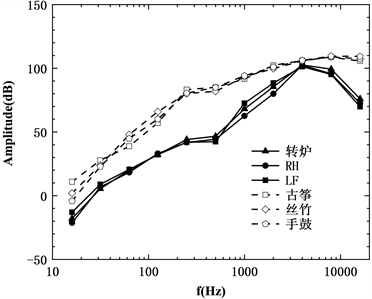
Figure 3. A-weighted octave of the sound

图3. A计权下声音的倍频程

3.3. 炼钢设备噪声现状

表1为不同炼钢设备噪声的A计权下总声压级。LF炉、RH炉和转炉的总声压级强度基本相当，均超过100 dB(A)，都高于国家标准的90 dB(A)。其中，转炉运行时噪声强度最大，高达104.56 dB(A)；而LF炉运行时噪声强度最小，但也高达101.84。因此，操作人员在这些设备附近开展工作时，需要佩带耳塞等设备进行降噪从而保护听力。

Table 1. Total sound pressure level of steel-making equipments on the base of A-weighted sound level

表1. A计权声级下炼钢设备的总声压级

3.4. 炼钢设备的分形维数和信息维数

表2表明，不同炼钢设备噪声的分形维数基本相同。其中，炼钢设备噪声时域信号的盒维数为1.008~1.011，时域信号变分估计分形维数约为1.308~1.31，频谱信号的信息维数约为4.109~4.159。

Table 2. Fractal dimension and information dimension of noise for steel-making equipments

表2. 炼钢设备噪声的分形维数和信息维数

表2还表明，乐声时域信号的盒维数大于1.017，大于炼钢设备噪声的盒维数；乐声时域信号的变分估计分形维数大于1.321，也大于炼钢设备噪声的变分估计分形维数。但是乐声频谱信号的信息维数为4.139~4.160，与炼钢设备噪声的信息维数范围4.109~4.159有部分区域重合。换言之，声音时域信号的分形维数能较好地区分炼钢厂噪声和乐声，而声音频域信号的分形维数则无法区分炼钢厂噪声和乐声。

4. 结论

1) 炼钢厂噪音的特点是强扰动的随机出现，振幅的切换整体上呈现随机无节奏。音乐时域信号可能出现等幅振荡，也可能出现纺锤形，强弱切换的时间量级为0.1秒。

2) 不同炼钢设备(转炉、LF炉、RH炉)噪声在A计权下声压的倍频程变化规律相似；乐器(古筝、江南丝竹和手鼓)乐声在A计权下声压的倍频程变化规律相似。乐器乐声的倍频程高于炼钢设备噪声。

3) 不同炼钢设备(转炉、LF炉、RH炉)的噪音具有不同频率的音强和音高变化混乱、音量过大的特点；乐器(古筝、江南丝竹和手鼓)乐声的特点是不同频率音高和音强变化平缓的特点。

4) 炼钢设备(转炉、LF炉、RH炉)噪声的盒维数约为1.01，变分估计分形维数约为1.31，信息维数约为4.1。

5) 声音时域信号的分形维数(盒维数和变分估计分形维数)能区分炼钢厂噪声和乐声，而声音频域信号的分形维数则无法区分炼钢厂噪声和乐声。

6) 通过对钢厂不同炼钢设备噪音特性分析及与不同乐器乐声特性对比，为钢厂治理噪音提供参考依据。

基金项目

国家自然科学基金委员会——宝钢集团有限公司钢铁联合研究基金(U1460108)。