1. 引言
在过去几十年里,关于复杂网络的研究越来越多 [1] [2] [3] [4] [5],其中一个最重要的原因是其在数学、物理、生物和工程等领域都具有潜在的应用。值得注意的是,现有关于复杂网络的研究成果主要适用于单连接网络,但多重连接网络在实际世界中普遍存在,例如:人际关系网络,交通网络,通信网络和细胞网络等。多重连接网络是指网络中节点之间具有多种类型的边连接,例如:在交通网络中,各个城市间的连接可能存在火车、高铁、飞机、轮船等不同类型的交通方式。由于实际背景的因素,我们不能简单地将节点之间不同类型的连接方式合并为一种,例如,不同类型的交通方式的速度是不一样的,所以人们会根据自身的需求,选择合适的交通方式。因此,如果用单连接网络来建模交通网络,这往往是不合适的。另外,相比于单连接网络,多重连接网络具有提高网络速度 [6]、优化网络性能 [7],降低运输成本等优点。并且单连接网络是多重连接网络的一种特殊情况。所以本文重点研究一类多重连接网络,这是具有现实意义的。
同步是复杂网络的重要集体现象之一并且在实际世界中广泛存在,例如:萤火虫同频率地发光和鸟群同步迁徙等,另外同步在安全通信 [8] 和图像处理 [9] 等多种领域具有潜在的应用。因此,同步引起了很多学者的关注并且大量的同步现象已经被研究 [2] [3] [4] [5]。众所周知,网络不能自发地实现同步,控制是使网络实现理想的同步状态的有效和必要手段。并且一些关于多重连接网络的同步策略 [10] - [18] 已经被研究。例如:文 [11] 通过设计自适应牵制控制器使得一类具有时滞和多重连接的双层非线性耦合网络实现了聚类同步。文 [12] 通过设计了间歇牵制控制器使得一类含时滞的多重连接网络实现同步。文 [14] 研究了一类具有时滞或时变时滞的多重连接网络的有限时间函数投影同步问题。
虽然已经得到一些关于多重连接网络的同步策略,但以下问题还有待进一步讨论:
首先,现实网络中的节点通常是不同的,甚至是具有不同的状态维数。文献 [3] [5] [19] 已经提出了具有不同状态维数节点的单连接复杂动态网络的同步策略。但具有不同状态维数节点的多重连接网络的同步问题的研究仍然是空缺的。这不仅因为由不同维数节点组成的多重连接网络通常表现出更复杂的动态行为,还因为描述不同维数节点间的同步现象比较困难。众所周知,完全同步 [10] [12] [16] 和有限时间同步 [18] 只发生在具有相同维数的节点之间。因此,需要引入一种新的同步现象来描述具有不同维数节点组成的多重连接网络的同步。而广义同步可描述不同维数节点之间的同步现象,例如,文 [7] 通过给关键节点设计控制器使一类具有不同维数节点的复杂网络分别实现渐近和指数广义投影同步。但文 [7] 研究的是单连接网络且是渐近和指数广义投影同步,这意味着网络将在无限时间达到同步。但在一些现实情况下,我们更希望网络能在有限时间内达到同步,例如在安全通信网络。另外,有限时间同步具有收敛快和低成本等优点。因此,本文研究具有不同维数节点的多重连接网络的有限时间广义同步问题,这是非常具有现实意义的且仍然是一项空缺,而本文致力填补这一项空缺。
其次,前述有关多重连接网络的研究成果 [10] - [18] 中,常常需要假设网络的外耦合矩阵是时不变的和需要满足耗散条件的,即每一重外耦合矩阵的每一行需要满足零行和条件。这一假设设置的主要原因是可以给推导过程提供一些便利。但这一假设并不总是适用于现实网络。事实上,现实网络中节点之间的耦合关系往往是随时间改变的,例如:在鸟群、鱼群,蜂群等自然网络中,个体通常能够形成或者抑制自身与其他个体之间的联系,并调整其耦合强度 [20]。另外,节点之间的耦合关系在上述自然网络中也并非简单地满足耗散条件,而是已经被自然所设计好以满足某种特定的需求,且是非线性函数的形式 [20]。此外,非耗散耦合系统在实际世界中普遍存在,如:价格网络、交通网络和颗粒材料 [21] [22] 等。因此,非常有必要研究非耗散耦合的时变多重连接网络的同步问题。
最后,现实网络中的节点通常具有几乎相同或者相似的性质、外观或者功能等特性,这些特性被叫做相似性,具有相似性的节点称作相似节点 [3] [23],例如:由几个单位相同的电厂组成的电网 [24],功能相似的神经元组成神经元群等。此外,一些研究表明相似性还可以简化控制器的设计 [3] [23]。但现有关于多重连接网络的文献中,还未考虑并利用节点的这一特性,本文将在这方面做一些研究。
受以上讨论启发,本文的重点是通过节点间的相似性,为具有不同维数节点和非耗散耦合的多重连接网络设计有限时间广义同步控制器。主要贡献如下:1) 与文献 [10] - [18] 相比,本文的多重连接网络模型能更好地体现现实网络的特征。不仅体现在研究的是具有不同维数节点和相似节点的多重连接网络,还体现在外耦合矩阵是时变且非耗散的。2) 探讨的是多重连接网络的有限时间广义同步现象,它不仅可以节约控制成本和估计达到同步的时间,还可以描述不同维数节点间的同步现象,是比现有文献 [10] - [18] 中的同步更广泛的同步现象。3) 采用分散控制实现多重连接网络的有限时间广义同步问题,分散控制因只利用节点自身的信息而具有低维、低消耗、易操作的优点。
符号规定:本文将采用标准符号,除特别说明外,
表示n阶单位矩阵,
表示n维零向量,
表示n维实向量集,
表示
维的实矩阵集,
表示矩阵P的转置矩阵,
表示对角元素为
的对角矩阵,
表示向量的欧几里得范数或矩阵的Frobenius范数。
2. 问题描述与预备知识
本文考虑一类非耗散耦合的多重连接网络模型,其由N个不同维数的节点和h种不同类型的连接组成,动力学方程为:
(1)
其中,
是节点i的状态向量,
是节点i的状态维数,
;
是非线性函数向量;
是充分光滑的向量值映射;
是第q种连接类型
的内耦合函数矩阵;
和
分别是控制增益矩阵和控制输入。设
是
t时刻网络(1)的第q种连接类型的时变外部耦合矩阵,它描述了t时刻网络(1)中各节点之间的耦合强度和拓扑结构,其元素即外耦合连接权值定义为:在t时刻,如果从节点i到节点j之间第q种连接类型有信息传输,则
,否则
,
是任意给定的实数,
。
注1 考虑多重连接网络(1)。(I) 由网络(1)可以清楚地看出,
是时变的、非对称的且是非耗散的,换句话说,即不要求
,与文献 [10] - [18] 相比,本文极大地放松了
对
的限制。另外网络(1)既可以很好地描述一些有向网络(
),也可以描述无向网络,网络中节点的关系既可以是合作的(
),也可以是竞争的。(II ) 值得注意的是,网络(1)中节点的维数是不同的,这说明本文的网络模型(1)比具有相同节点或具有相同维数的不同节点的多重连接网络 [10] - [18] 更具有代表性。(III) 网络(1)中的内耦合矩阵也是非线性的,这不同于文献 [10] - [18]。综上,本文的多重连接网络模型比文献 [10] - [18] 具有更高的研究价值和意义。
下面给出有限时间广义同步的定义以及本文要用到的引理:
不失一般性,令
是多重连接网络(1)中节点的参考轨迹并且满足
。
定义1 考虑网络(1)。如果存在一个时刻
,满足
,
,并且当
时,有
成立,则称网络(1)与参考目标
之间实现了有限时间广义同步,本文将
称作达到有限时间广义同步时间。
注2 定义1包含了一些同步现象,例如当节点的状态维数
相同且
时,则定义1表示有限时间完全同步 [18] [25],当
,
,定义1则表示有限时间矩阵投影同步。
引理1 [26] 如果
和
,则
。
引理2 [27] 假设
是连续正定函数且满足以下微分不等式:
其中,
都是常数。则对于任意的
,
满足以下微分不等式:
且
其中
。
假设网络(1)满足以下条件:
假设1 [3] [23] 考虑网络(1)所对应的各受控孤立节点。不失一般性,选取第一个节点作为参考节点。假设存在N个状态反馈控制器
,
,使得
(2)
(3)
成立,其中
和
分别是光滑映射和光滑可逆函数矩阵。
是
的Jacobi矩阵。
注3 由文献 [3] [23] 可知,假设1所描述的多重连接网络(1)中孤立节点间具有相似性。另外,
称为节点i与节点1之间的一组相似参量,一般地,节点间存在多组相似参量。
假设2 记
。存在已知正常数b和m使得对所有的
,有
,
成立。
假设3 函数矩阵
是行满秩的,即存在右逆矩阵
使得
成立。
3. 主要结果
控制目标:根据定义1,为多重连接网络(1)设计分散自适应控制器
使得
成立,其中
是节点i的有限时间广义同步误差,其中
。
定理1 考虑多重连接网络(1)。如果假设(1)~(3)成立,则网络(1)在分散控制器
(4)
和自适应律
(5)
的控制下能实现定义1意义下的有限时间广义同步,其中
都是待定可调的参数,且
,
都是假设2中的正常数,
,
,
。
证明:由多重连接网络(1)、假设1和分散控制器(4)可得出有限时间广义同步的误差动力学方程为:
(6)
选择Lyapunov候选函数为:
(7)
则根据自适应律(5)可以推出
沿误差系统(6)的导数为:
(8)
注意到,由假设2可得
(9)
将(9)式带入(8)式,可得
(10)
由于参数
是可调节的,所以一定存在一个充分大的
使得
成立。接下来,如果存在
使得
时,则
,说明网络(1)与参考目标
在确定的时刻
达到了同步;如果当
时,有
,
成立,以及
,
,可得:
(11)
根据引理1,有
(12)
则由式(12)可知引理2中的
和
分别为:
,则由式(12)和引理2可知
,
,其中,
,且当
时,
。这说明,
以及
当
时,有
成立。因此,网络(1)与参考目标
达到有限时间广义同步。定理1证毕。
注4 由
可知,网络(1)的同步时间依赖于
,当
增加时,网络(1)的同步时间越短,
这将体现在数值仿真部分。此外,与渐近同步 [10] [12] [16] 相比,有限时间同步能有效地避免网络在时间趋于无穷时达到同步的问题,与完全同步 [10] [12] [16] 和有限时间同步 [18] 相比,广义同步可以描述不同维数节点间的同步现象,因此有限时间广义同步具有更强的实用性。
4. 数值仿真
在这一部分给出数值仿真实例来验证定理1的有效性和正确性。考虑由
个不同维数的节点和
种不同的连接类型组成的非耗散耦合多重连接网络(1),其孤立节点的状态方程分别为:
(13a)
(13b)
其中
。(13)式表明节点
的维数为
。参考轨迹
的状态方程为
。
注5 由式(13)可知,第一个节点为Lü混沌吸引子 [28],第二个节点为超混沌Lü吸引子 [29],以及每个节点都是非线性且具有各不相同的状态维数,这不同于文献 [10] - [18]。
不失一般性,多重连接网络(1)和控制器(4)中的其他参数选取如下
(14)
(15)
(16)
(17)
(18)
(19a)
(19b)
其中
,可以验证式(14)~(19)中的参量满足假设1~3。另外,从式(19)可以看出
是非线性的函数矩阵,这不同于文献 [10] - [18] 中的内耦合矩阵是常数矩阵。
不失一般性,外部耦合矩阵
选取如下
(20a)
(20b)
其中
是由Matlab产生的伪随机数,
。
注6 从式(20)可以看出,外部耦合矩阵
是时变的、非对称的、非耗散的。网络(1)中节点之间可以是合作关系,也可以是竞争关系。这在极大程度上放松了对外部耦合矩阵的限制,与文献 [10] - [18] 不同。
选择初值
,
以及(5)式中的
如下
(21a)
(21b)
以及选择控制器(4)和自适应律(5)中的其他参数如下
(22)
其中
,
和
是由Matlab产生的维数为
和3的伪随机向量。
下面运用定理1的同步方案来仿真具有参数(13)~(22)的多重连接网络(1)的有限时间广义同步,其同步误
差曲线如图1所示。记多重连接网络(1)的总同步误差为
,其中
。
 (a)
(a) 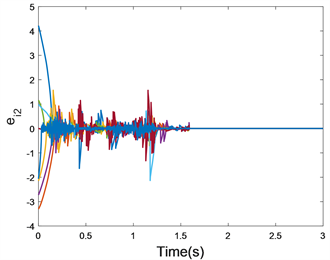 (b)
(b)  (c)
(c)  (d)
(d)
Figure 1. The time response curves of finite-time generalized synchronization errors of multi-linked network (1) with parameters (13)~(22) under the control scheme of Theorem 1. (a)
, (b)
, (c)
, (d)
图1. 在定理1的控制方案下,具有参数(13)~(22)的多重连接网络(1)的有限时间广义同步误差响应曲线。(a)
,(b)
,(c)
,(d)
图1表明在控制器(4)和自适应律(5)的作用下,具有参数(13)~(22)的多重连接网络(1)实现了有限时间广义同步,且我们可以清楚地知道同步时间为
秒。这充分验证了同步定理1的有效性。
图2展示了在控制器(4)中的参数
对于网络(1)的有限时间广义同步的影响。简洁起见,通过总有限时间广义同步误差
反映不同
对于同步时间的影响。从图2可以看出,在控制器(4)和参数(13)~(22)的作用下,参数
越大,多重连接网络(1)达到同步的时间越短。因此,在现实网络中,可以根据实际需要调整网络达到同步时间。
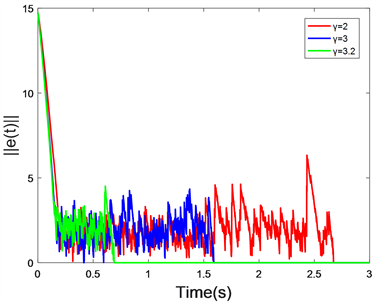
Figure 2. The time response curves of total finite-time generalized synchronization errors of multi-linked network (1) with different parameters
图2. 在不同参数
的作用下,网络(1)的总有限时间广义同步误差时间响应曲线
在自适应律(5)中的
的时间响应曲线如图3所示,从图3我们可以观察到,当时间趋于无穷时,
是一致有界的且趋于不同的常数。
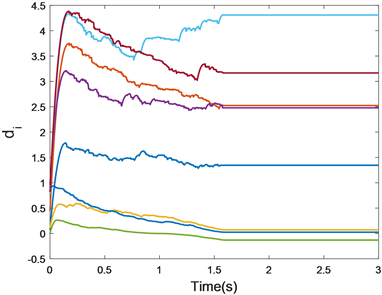
Figure 3. The time response curve of
图3.
的时间响应曲线
5. 结论
本文研究了一类具有不同维数相似节点和非耗散耦合的多重连接网络的有限时间广义同步控制问题。设计了分散自适应控制器,利用有限时间稳定性理论得到了这一类多重连接网络实现有限时间广义同步的充分条件。通过数值仿真实例验证了所提结果的有效性。值得指出的是,本文中的外耦合矩阵是时变的、非对称的和非耗散的,这与现存的多重连接网络模型相比,本文的网络模型中极大地放松了对外耦合矩阵的限制,适用范围更广。另外,有限时间同步有效地避免了网络在只能在无穷时间实现同步的问题,这对于多重连接网络在实际工程应用中具有重要意义,而且广义同步适用于不同维数节点之间的同步,可以提高控制策略的在现实网络中的可行性,因此有限时间广义同步具有更高的研究价值和意义。为了进一步减少控制成本,接下来将考虑利用间歇控制或者脉冲控制实现我们的多重连接网络的有限时间广义同步。
基金项目
广东省自然科学基金项目(2020A1515010809)。
NOTES
Email: 2966574399@qq.com