基于缠绕成型工艺的新型贮箱设计方法

A Design Method of Tank Based on Winding Forming Process

摘要: 为了提高运载火箭的运输效率以及降低火箭发射成本，采用复合材料贮箱代替金属贮箱是最直接、最有效的方式，本文提出一种新型无内衬复合材料贮箱的设计方案。针对某一尺寸的贮箱结构，采用平面缠绕的方法进行缠绕的线型设计，同时基于网格理论对缠绕的层数进行设计，提出贮箱筒段的缠绕方案；结合经典层合板理论，通过Tsai-Wu失效判据进行单角度强度校核保证贮箱整体结构的安全；提出上、下封头极孔处的连接结构形式以及通孔的设计过程；应用ABAQUS进行贮箱实体模型和设计内压下贮箱缠绕层、胶层和上下法兰连接结构的有限元模拟，讨论设计的贮箱结构的可行性和安全性。本文的研究工作为复合材料贮箱的成型加工提供了理论依据。

Abstract: In order to improve the transport efficiency of carrier rocket and reduce the launching cost of rocket, the composite material storage tank instead of metal storage tank is the most direct and effective way. In this paper, a new design scheme of non-lined composite material storage tank is proposed. The design of the winding line and the winding layer is carried out based on the plane winding and the grid theory, and the winding scheme of the tank cylinder segment is put forward ultimately. Based on the classical laminated plate theory and Tsai-Wu failure criterion, single-angle strength checking is carried out to ensure the safety of the overall tank structure. The connecting structure of the upper and lower head pole hole and the design of the through hole are presented. By using ABAQUS, the solid model of the tank is established, and the finite element simulations of the winding layer, rubber layer, upper and lower flange connection structure of the tank under internal pressure are carried out. The feasibility and safety of the designed tank structure are discussed, and the improvement scheme for the existing problems in the design is proposed. The research work of this paper provides a theoretical basis for the forming of composite storage tanks.

1. 引言

当今世界上，各航天大国的运载火箭正朝着高可靠、低成本、大直径等方向发展 [1]。2019年末进行“复飞”的长征五号遥三火箭，是中国由航天大国迈向航天强国的重要标志，也是中国载人航天工程第三步任务——空间站研制建设的关键所在。与国外的一些同级别的运载火箭相比，我国的长征五号运载火箭(如图1所示)的缺点是重量大、推力小。提升火箭的运载效率、降低火箭发射成本的最直接且有效的方式，就是火箭结构的轻质化。相关研究表明 [2] [3] [4]，推进剂贮箱占到整个运载火箭重量的60%左右，采用复合材料制造的贮箱相比传统的金属贮箱，不仅能够极大地减轻质量，而且可以极大提升其抗疲劳等性能。因此，大力开展复合材料贮箱研究具有至关重要的意义。

国外早在20世纪80年代就已经开始了无内衬复合材料贮箱的研究，其中最具代表性的是美国的NASA [5]。2001年NASA对外宣称，使用碳纤维增强树脂基复合材料通过缠绕工艺制备出无内衬的复合材料液氧贮箱，其直径为1.2 m，较同等规模的金属贮箱减重18%。2011年NASA发布了新项目，旨在使复合材料低温推进剂贮箱的制造技术更加成熟，包括2.4 m、5.5 m和10 m的贮箱设计制造能够满足未来的重型运载火箭和其它空间的应用，图2所示为NASA的5.5 m复合材料低温贮箱。

我国航天工业对复合材料的研究在20世纪70年代才刚刚开始，起步很晚。由于火箭贮箱涉及军工领域，国内很难获得相关资料，直到2002年我国才研制出带金属内衬的复合材料贮箱，取得了一些研究成果：朱平萍和刘宪力 [6] 以土星V为例分析了大型贮箱结构的特点和制造工艺，提出了大型贮箱结构形式以及贮箱制造技术发展趋势；辛腾达 [7] 等人运用材料力学等理论对金属贮箱进行了应力分析，推导出了贮箱结构各段的径向与环向应力解析式，最终确定了金属贮箱壁厚的几何参数，为以后的复合材料贮箱设计与优化打下理论基础；任明法 [8] 等人分别采用自适应模拟退火算法和下山单纯形算法对异性复合材料贮箱的铺层进行了设计优化，分析了两种算法的优缺点等。

目前，国内对于无内衬复合材料贮箱设计的研究非常有限。本文提出了一种新型无内衬复合材料贮箱的设计方案：采用平面缠绕的方法进行缠绕的线型设计，同时基于网格理论对缠绕的层数进行设计，提出贮箱的缠绕方案，以及筒段与上下封头之间的法兰连接结构的形式；应用有限元软件ABAQUS及其插件WCM进行贮箱结构的模型建立，对无低温载荷状态和低温载荷状态下的贮箱分别进行模拟分析，对比贮箱复合材料缠绕层的最大主应变云图以及内、外法兰盘等部分的最大主应力云图，证明了贮箱结构的安全性以及本文提出的新型贮箱设计方案的可行性。

Figure 1. The Long March V

图1. 长征五号

Figure 2. NASA’s 5.5 m composite cryogenic storage tank

图2. NASA的5.5 m复合材料低温贮箱

2. 贮箱结构

本设计中复合材料贮箱内部无金属内衬，整体结构和上下封头连接结构如图3 所示。贮箱直径为300 mm，总高度为299.86 mm，竖直筒段高度为112.5 mm，贮箱上、下封头为1/2椭球面，椭球长半轴为150 mm，短半轴为93.68 mm，缠绕的上、下极孔直径分别为120 mm和60 mm。图3(b)中法兰连接结构近似于将缠绕层“夹持”固定住，连接结构和缠绕层材料分别为6061铝合金和T700环氧树脂复合材料。

本论文在对复合材料贮箱结构进行设计时，仅考虑内压一种工况载荷，复合材料贮箱的设计内压为 0.8 MPa。

(a) (b)

Figure 3. Composite material storage tank. (a) Tank; (b) Connection structure

图3. 复合材料贮箱结构。(a) 贮箱；(b) 连接结构

3. 贮箱设计

对贮箱的复合材料层进行线型和层数设计，结合经典层合板理论 [9] [10] 采用Tsai-Wu理论进行单角度强度校核，以及对法兰连接结构进行设计。

3.1. 缠绕层设计

在进行结构设计时，从实际缠绕工艺的角度出发、考虑缠绕工艺的多种约束，进行贮箱缠绕角度等的设计，从而保证贮箱结构设计方案的合理性和可实现性。贮箱的上、下封头的缠绕极孔直径分别为120 mm和60 mm。缠绕方式采用湿法缠绕，实际的缠绕角应控制在与非测地线缠绕角的偏离值不超过±10˚，以保证在封头曲面上纤维不滑线。同时，对于同一个产品，宜采用多缠绕角进行缠绕，以免形成不稳定的纤维结构，导致在复杂的应力作用下树脂受过大的应力，本设计采用螺旋缠绕加环向缠绕交替进行的双缠绕角方法。由于完成一个螺旋缠绕循环时，包含了一个角度的正负两个缠绕层，因此，在进行设计和模拟时，正负缠绕的层数应该是一致的。在实际进行法兰连接结构制造时，为了方便缠绕的芯模进行脱模，需要在内法兰的内表面设置一个1˚~2˚的脱模角。

对于短而粗的壳体，常采用平面缠绕成型方法 [11] [12] [13] [14]，如图4所示。平面缠绕时，绕丝嘴在固定平面内围绕芯模作匀速圆周运动，芯模绕自轴慢速旋转，各纱片均与极孔相切，纤维缠绕轨迹近似为一个在平面单圆封闭曲线。筒身段的缠绕角 $\alpha$ 在平面上的投影可视为一常数。与等应力封头不同， $\alpha$ 不是由筒身半径与极孔半径之比决定的，而是由结构的几何尺寸确定的。筒身螺旋缠绕角可用式(1)计算：

$\tan \alpha =\frac{y_1+y_2}{l_0}=\frac{r_1+r_2}{l}$ (1)

计算式(1)并取整得筒身段的螺旋缠绕角为17˚。

Figure 4. Plane winding

图4. 平面缠绕成型

铺层的初步设计采用网格理论，即不考虑树脂的刚性，又认为壳体的薄膜内力全部由连续的纤维构成的网状结构来承担，采用截面法和静力平衡条件，轴向单位内力 $N_{\phi }$ 和周向单位内力 $N_{\theta }$ 表示为式(2)：

$\begin{array}{l}{N}_{\phi }=\frac{1}{2}RP\\ N_{\theta }=RP\end{array}$ (2)

其中R和P分别为筒体半径和容器承受的内压强。

由于结构设计以及工艺要求，圆筒形压力容器常采用两组或者多组缠绕角来缠绕。本设计采用螺旋缠绕加环向缠绕的双螺旋缠绕，由静力平衡可以求得，螺旋缠绕层纤维厚度 $t_{f\alpha }$ 和环向缠绕层纤维厚度 $t_{f90}$ 为式(3)：

$\begin{array}{l}{t}_{f\alpha }=\frac{1}{2{\left(\cos \alpha \right)}^2}\cdot \frac{RP}{\left[{\sigma }_f\right]}\\ t_{f90}=\frac{2-{\left(\tan \alpha \right)}^2}{2}\cdot \frac{RP}{\left[{\sigma }_f\right]}\end{array}$ (3)

其中， $\left[{\sigma }_f\right]$ 是纤维的许用应力，取4.2 GPa。引入螺旋缠绕纤维强度利用系数k，实际螺旋缠绕纤维厚度为

$t_{f\alpha 实}=t_{f\alpha }/k$ (4)

将贮箱参数代入式(3)，式(4)中的纤维强度利用系数k取0.7，得螺旋缠绕层的纤维厚度为0.0223 mm，环向缠绕层的纤维厚度为0.0273 mm，考虑到气密性和实际工艺的约束取缠绕顺序及层数如表1所示：

Table 1. Winding order

表1. 缠绕顺序

筒身段在轴向力和周向力的作用下的应变为式(5)：

$\left(\begin{array}{c}{\epsilon }_{\phi }\\ {\epsilon }_{\theta }\end{array}\right)={\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]}^{-1}\left(\begin{array}{c}{N}_{\phi }\\ N_{\phi }\end{array}\right)$ (5)

其中A_ij为拉伸刚度矩阵A的分量，假设层合板是由k个单层板叠合而成的，并且在每个单层组内模量 ${\bar{Q}}_{ij}^{\left(k\right)}$ 不变，则A_ij可写做式(6)：

$A_{ij}={\displaystyle {\int }_{-h/2}^{h/2}{\bar{Q}}_{ij}^{\left(k\right)}\text{d}z}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{\bar{Q}}_{ij}^{\left(k\right)}\left(z_k-z_{k-1}\right)}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{\bar{Q}}_{ij}^{\left(k\right)}{t}_k}$ (6)

其中t_k为k单层组的厚度， ${\bar{Q}}_{ij}^{\left(k\right)}$ 为k单层组的偏轴模量。

式(6)中的偏轴模量 ${\bar{Q}}_{ij}^{\left(k\right)}$ 可由式(7)求得：

$\begin{array}{l}{\bar{Q}}_{11}=Q_{11}{c}^4+2\left(Q_{12}+2Q_{66}\right)c^2{s}^2+Q_{22}{s}^4\\ {\bar{Q}}_{22}=Q_{11}{s}^4+2\left(Q_{12}+2Q_{66}\right)c^2{s}^2+Q_{22}{c}^4\\ {\bar{Q}}_{12}=\left(Q_{11}+Q_{12}-4Q_{66}\right)c^2{s}^2+Q_{12}\left(c^4+s^4\right)\\ {\bar{Q}}_{16}=\left(Q_{11}-Q_{12}-2Q_{66}\right)c^{3}s-\left(Q_{22}-Q_{12}-2Q_{66}\right)c{s}^3\\ {\bar{Q}}_{26}=\left(Q_{11}-Q_{12}-2Q_{66}\right)c{s}^3-\left(Q_{22}-Q_{12}-2Q_{66}\right)c^{3}s\\ {\bar{Q}}_{66}=\left(Q_{11}+Q_{22}-2Q_{12}\right)c^2{s}^2+Q_{66}{\left(c^2-s^2\right)}^2\end{array}$ (7)

其中 $c=\cos \left(\alpha \right)$， $s=\sin \left(\alpha \right)$， $\alpha$ 为纤维在筒身段的缠绕角，主轴刚度矩阵Q分量为式(8)：

$\begin{array}{l}{Q}_{11}=\frac{E_1}{1-{\upsilon }_{12}{\upsilon }_{21}},Q_{22}=\frac{E_2}{1-{\upsilon }_{12}{\upsilon }_{21}}\\ Q_{12}=\frac{{\upsilon }_{12}{E}_2}{1-{\upsilon }_{12}{\upsilon }_{21}},Q_{66}=G_{12}\end{array}$ (8)

其中E₁，E₂，G₁₂和 $\upsilon$ 分别是复合材料单层板的横向及纵向拉伸模量，剪切模量和泊松比。

由式(5)和式(7)得偏轴应力为式(9)

$\left(\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right)=\left(\begin{array}{ccc}{\bar{Q}}_{11}& {\bar{Q}}_{12}& {\bar{Q}}_{16}\\ {\bar{Q}}_{21}& {\bar{Q}}_{22}& {\bar{Q}}_{26}\\ {\bar{Q}}_{61}& {\bar{Q}}_{62}& {\bar{Q}}_{66}\end{array}\right)\left(\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\end{array}\right)$ (9)

其中 ${\gamma }_{xy}=0$,引入转换矩阵T，最终可得到纤维方向的正轴应力为式(10)

$\left(\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\tau }_{12}\end{array}\right)=T\bar{Q}\left(\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\end{array}\right),T=\left(\begin{array}{ccc}{c}^2& s^2& 2cs\\ s^2& c^2& -2cs\\ -cs& cs& c^2-s^2\end{array}\right)$ (10)

应用Tsai-Wu失效判据式可以对设计出的各个缠绕角是否失效进行校核及层数优化，各单层的Tsai-Wu系数均远小于1，说明贮箱结构安全。

3.2. 法兰连接结构设计

在复合材料层设计完成后需要对贮箱极孔处的连接结构进行设计，如图3(b)所示。连接结构拟采用6061铝合金材料，连接结构包括内法兰与外法兰，内法兰的外壁与外法兰的内壁以螺纹拧紧配合，在外法兰上表面设置密封槽和一定数量的通孔用于螺栓连接。法兰连接结构与缠绕层通过胶接连接，然后进行纤维缠绕实现整体结构固化成型，最终完成贮箱装配。

为方便贮箱与盖板螺栓连接，将16个通孔设置在外法兰的延伸部分，上、下法兰连接结构的通孔直径分别为6 mm和4 mm。

4. 贮箱结构的有限元模拟

4.1. 贮箱有限元模型

复合材料贮箱的有限元模型如图3(a)所示。模型从上至下包括三部分：极孔为120 mm的法兰连接结构，复合材料缠绕层和极孔为60 mm的法兰连接结构。有限元模型的复合材料缠绕层部分，使用复合材料缠绕插件WCM建模并划分单元，划分方法使用扫掠方法，单元类型为C3D8，单元数量为380000；连接结构采用常规建模，同样使用扫掠方法划分单元，单元类型为C3D8R，总单元数量为329456。载荷条件为设计压力0.8 MPa。由于螺纹模拟的复杂性，对螺栓连接进行简化处理，以集中力施加在通孔下边缘的形式模拟。边界条件为对贮箱竖直段中线施加轴向对称约束。对常温环境和低温环境下的贮箱分别进行有限元模拟，低温环境设置为−196℃。贮箱模型中的上、下法兰连接结构尺寸并不相同，将分别进行模拟。

4.2. 缠绕层有限元模拟

图5所示为贮箱结构的复合材料缠绕层在常温环境和低温环境下的最大主应变云图。由图5(a)可见，复合材料缠绕层的最大主应变的最大值为2227 με、位于竖直筒段上边沿，这是因为在该螺旋缠绕与环向缠绕过渡处，由于缠绕角度的变化使得该处产生了应力集中。由图5(b)可见，整个复合材料缠绕层的最大主应变值均为负值：最大主应变为−5491 με位于贮箱竖直筒段下边沿，与图5(a)类似也是螺旋缠绕与环向缠绕过渡处的应力集中所导致的；除此以外，大部分区域的最大主应变值分布比较均匀、为−5000 με左右。两种情况下的最大主应变值均远远小于T700复合材料的许用应变15000 με，所以，在常温和低温环境下贮箱的复合材料缠绕层均安全可靠。

(a) (b)

Figure 5. The maximum principal strain cloud diagram of the composite winding layer of the tank. (a) At room temperature; (b) At low temperatures

图5. 贮箱复合材料缠绕层的最大主应变云图。(a) 常温环境；(b) 低温环境

4.3. 胶层有限元模拟

图6所示为贮箱胶层在常温环境和低温环境下的最大主应力云图，由图6可见，两组胶层的应力分布都较为均匀，在低温载荷作用下的胶层应力略小于常温载荷作用下的胶层应力，说明选用的粘结剂比较合理。由图6(a)可见，常温环境下胶层的最大主应力的最大值是11.89 MPa、小于环氧树脂许用应力20 MPa，最大值发生在与下法兰连接结构端部接触的位置，这是因为法兰盘延伸部分的端部存在尖角、出现了应力集中现象。在实际生产中，法兰盘端部会带有一定的圆弧过渡，则实际的胶层最大主应力值将会小于计算值，这必是安全的。由图6(b)可见，低温环境下胶层的最大主应力的最大值达到41.81 MPa、位于与法兰盘约束的区域附近。这是由于粘结剂和铝合金材料的热膨胀系数不匹配引起的，这就需重新选择法兰盘材料或对粘接剂进行调整来解决。除此区域以外，整个胶层的应力分布较为均匀，大小在7 MPa左右。

(a) (b)

Figure 6. The maximum principal stress cloud of the rubber layer of the tank. (a) At room temperature; (b) At low temperatures

图6. 胶层的最大主应力云图。(a) 常温环境；(b) 低温环境

4.4. 法兰连接结构有限元模拟

图7和图8所示分别为在常温和低温环境下贮箱上、下法兰连接结构的应力云图。由图7可见，上、下法兰连接结构的最大主应力的最大值分别为100.4 MPa和90.39 MPa，分别位于上外法兰的通孔周围和下内法兰的边缘处、为应力集中造成，应力值远小于铝合金的屈服强度276 MPa，连接结构安全。由图8可见，上、下法兰连接结构的最大主应力的最大值分别为274.4 MPa和298.4 MPa。

(a) (b)

Figure 7. The maximum principal stress cloud of connection structure of storage tank at room temperature. (a) Stress cloud diagram of upper flange; (b) Stress cloud diagram of lower flange

图7. 常温环境贮箱上下法兰连接结构最大主应力云图。(a) 上法兰；(b) 下法兰

(a) (b)

Figure 8. The maximum principal stress cloud of connection structure of storage tank at low temperatures. (a) Stress cloud diagram of upper flange; (b) Stress cloud diagram of lower flange

图8. 低温环境贮箱上下法兰连接结构最大主应力云图。(a) 上法兰；(b) 下法兰

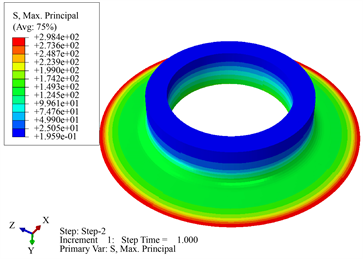
将上、下法兰连接结构的内、外法兰盘在低温环境下做进一步分析，图9和图10分别为低温环境上连接结构内、外法兰的最大主应力云图。由图9(a)可见，上法兰结构的内法兰最大主应力值发生在内法兰盘延伸部分的尖角处，究其原因一方面该处由于存在尖角导致了应力集中，另一方面，由于粘结剂和铝合金材料的热膨胀系数不匹配引起的应力值偏大，最终使整个内法兰盘延伸部分的最大主应力值均偏大一些、达到最大值274.4 MPa，因此，需要重新选择法兰盘材料或调整粘接剂进行解决。由图9(b)可见，最大主应力值达到234.8 Mpa、位于通孔附近的某一块单元，为应力奇异引起的，实际法兰结构不会存在应力奇异；整个外法兰盘在通孔、密封槽和法兰盘直角过渡处普遍存在应力集中，最大主应力值在70 MPa左右，在允许范围内。与上法兰连接结构类似，由图10(a)和图10(b)可以得到相似结论，下连接外法兰结构应力值不超过铝合金的屈服强度，而内法兰延伸部分同样是由于材料热膨胀系数不匹配问题导致应力值稍高于允许值，须重新选择法兰盘材料或调整粘接剂参数。

(a) (b)

Figure 9. The maximum principal stress cloud of the upper connection of storage tank at low temperatures. (a) Stress cloud of the inner flange; (b) Stress cloud of the outer flange

图9. 低温环境贮箱上连接的最大主应力云图。(a) 内法兰；(b) 外法兰

(a) (b)

Figure 10. The maximum principal stress cloud of the lower connection of storage tank at low temperatures. (a) Stress cloud of the inner flange; (b) Stress cloud of the outer flange

图10. 低温环境贮箱下连接的最大主应力云图。(a) 内法兰；(b) 外法兰

5. 结论

本文提出了一种新型无内衬复合材料贮箱的设计方案。针对某一尺寸的贮箱结构，采用平面缠绕的方法进行缠绕的线型设计，同时基于网格理论对缠绕的层数进行设计，提出贮箱筒段的缠绕方案，结合经典层合板理论通过Tsai-Wu失效判据进行单角度强度校核，提出了上、下封头极孔处的连接结构形式以及通孔的设计过程。在复合材料贮箱的设计内压工况下应用ABAQUS对贮箱缠绕层、胶层和上下法兰连接结构进行了有限元模拟，讨论了贮箱结构的可行性和安全性。本文的研究工作为复合材料贮箱的成型加工提供了理论依据。

致谢

感谢国家重点研发计划项目(2018YFA0702800)对本文工作的支持。

参考文献

NOTES

^*通讯作者。