1. 引言
本文考虑如下一维非线性Allen-Cahn方程的初边值问题(IBVP),
(1.1)
这里u表示二元合金中的一个金属部件的浓度,
表示接口的宽度,非线性项
,
为
的内部点。
早在1979年,Allen和Cahn在描述晶体中的反相位边界运动时引入Allen-Cahn方程 [1],此后,它被广泛用于描述各种应用问题,比如,相变 [2] [3]、晶体 [4] [5] 生长和图像分析 [6] [7]。此类相场模型的方程本身具有一定的复杂性且无真解的解析表达式,故需要精确有效的数值格式来进行求解,因此研究该方程的数值解求解方法就显得格外重要。
众所周知,IBVP(1.1)有两个重要的性质,其一是能量稳定性,一维非线性Allen-Cahn方程具有如下的能量函数:
(1.2)
该能量函数随时间递减;其二是该方程的精确解满足最大化原则。这两点性质在研究Allen-Cahn方程高效的数值解法中发挥重要作用。
目前关于Allen-Cahn方程的数值逼近学者们做了很多工作。2010年, [8] 中Shen等对Allen-Cahn方程和Cahn-Hilliard方程建立了三种格式,并进行了能量递减稳定分析和误差分析; [9] 中张佳琪等考虑了三种离散格式,证明了所建立的数值格式满足离散最大化原则和能量衰减性; [10] 中汤涛等建立一阶隐显格式证明了Allen-Cahn方程的最大化原则及其无条件稳定性,并给出误差分析; [11] 中Shen等研究了具有非线性迁移率的广义Allen-Cahn方程,建立了在时间方向半离散的格式和完全离散格式; [12] 中Hou等提出了分数阶空间Allen-Cahn方程的二阶Crank-Nicolson有限差分格式,这项工作的主要贡献之一是证明了在合理的时间步长约束下,数值解满足离散极大值原理;基于最大稳定性,建立了全离散格式的非线性能量稳定性,并研究了相应的误差估计,数值实验验证了理论结果; [13] 中Hou等采用有限差分法求解含有小扰动得到最大范数下的离散有界稳定性; [14] 中乔寒月等建立了全离散紧差分格式,证明了在合理的步长比和时间步长的约束下,其数值解满足离散最大化原则,此外还研究了全离散格式的能量稳定性,这对一维带有边界条件的非线性Allen-Cahn方程的数值逼近又增添一种有效可行的方法。
本文通过构造显式保结构有限差分方法(简称SP-DFFT-FDMs)对IBVP(1.1)进行数值求解。文章其余部分安排如下,在第二节,给出一些必需的符号和辅助引理以及差分格式的建立;第三节从离散最大化原则、离散能量稳定性和收敛性三个方面进行数值分析;第四节,数值算例验证了理论分析的正确性;第五节给出一些结论。
2. 符号及引理
在建立差分格式前,先介绍一些符号和引理。首先,对求解区间
进行剖分,取空间步长
,
,时间步长
,
均为整数,
,对时间方向和空间方向剖分形成的网格定义如下:
此外,记网格空间
。记
为
上的网格函数,取网格函数
,定义如下算子:
对于任意的
,定于如下内积和范数:
引理2.1 ( [15])设
为非负序列,且满足
其中c和g为非负常数,则有
3. 差分格式的建立
记
和
分别表示问题IBVP(1.1)的精确解和数值解,常数C为不依赖网格参数,不同的情形下取不同的值。
在结点
处考虑IBVP(1.1)有
(3.1)
由带拉格朗日余项的泰勒展开式得
(3.2a)
(3.2b)
(3.2c)
(3.2d)
(3.2e)
其中
为稳定项。记
,将(3.2a)~(3.2e)代入(3.1)中,得
(3.3a)
(3.3b)
(3.3c)
其中
(3.4)
显然存在一个正常数C,使得
. (3.5)
由于差分格式(3.3a)是三层格式,已知第0层的数值解,为了启动数值模拟,第1层的数值解采用以下格式( [10])计算:
(3.6)
其中
(3.7)
在(3.3a)~(3.3c)和(3.6)中,忽略
和
,用数值解
代替精确解
,得到差分格式SP-DFFT-FDMS:
(3.8a)
(3.8b)
(3.8c)
(3.8d)
稳定化差分格式SP-DFFT-FDMS具有
形式的截断误差。
4. 数值分析
本节,将给出差分格式SP-DFFT-FDMS的一些性质:离散最大化原则和离散能量稳定性。
引理4.1 ( [16])对于任意的
,都有
引理4.2 ( [16])对于任意的
和网格函数
,有以下成立:
引理4.3对于任意的网格函数
,有以下成立:
证 结合文献 [16] 中,
,以及
,有
4.1. 离散最大化原则
定理4.1假设
,当
时,有如下成立:
(4.1)
证 应用数学归纳法证明,显然
。根据文献 [10],可得
。假设当
时,有
成立,接下来,证明对于
结果依然成立。
现假设当
时,记
,可将差分格式SP-DFFT-FDMS中的(3.8a)改写为
(4.2)
是有关于
和
的函数,结合
和归纳假设
,易得
(4.3)
(4.4)
此外,通过简单的计算可知
(4.5)
其中
(4.6)
由(4.3)~(4.5)可得,关于
的函数
是单调递增的,注意到
。有如下结果
(4.7)
结合
,可得
。证毕。
4.2. 离散能量稳定性
本节研究差分格式的稳定性,定义如下相应的离散能量
:
(4.8)
记
(4.9)
定理4.2假设
是差分格式SP-DFFT-FDMS的数值解,则有如下成立:
(4.10)
证 将(3.8a)与
作内积,对j从1到
求和,可得
(4.11)
可将(4.11)改写为如下形式
(4.12)
显然有
,
。证毕。
4.3. 差分格式解的收敛性
本节考虑差分格式数值解的收敛性。首先给出一个重要的引理,这将用于后续的收敛性分析。
引理3假设有如下成立
则有
证 结合
与不等式
,易得
应用引理1,可得
易得,
。证毕。
假定
为IBVPs(1.1)的精确解,则存在正整数C,使得
(4.13)
(4.14)
定理4.3假设
。
为IBVP(1.1)的数值解,
为精确解,定义误差为
,
。有
(4.15)
证 将(3.8a)~(3.8d)与(3.3a)、(3.6)相减,得到如下误差方程:
(4.16a)
(4.16b)
(4.16c)
将(4.16b)与
作内积,对j从1到
进行求和,得
(4.17)
结合(4.13),有如下成立:
(4.18)
(4.19)
此外,由引理3可得
(4.20)
将(4.16a)与
作内积,对j从1到
进行求和,得
(4.21)
假设
,
,应用不等式
,可得
(4.22)
(4.23)
(4.24)
(4.25)
取
,将(4.22)~(4.25)代入(4.21)整理得
(4.26)
在上式两边同乘
,用l取代k,对l从0到k进行求和,可得
(4.27)
当
时,应用引理2.1,有如下成立:
(4.28)
证毕。
在分析最大化原则时,本文所建立的格式满足最大化原则要求
的条件略强于文献 [10] [13],但该格式为显式格式,计算效率高且能长时间稳定模拟,此外还有程序易实现的优点。
5. 数值算例
本节将给出数值算例来验证得到前几节所得的理论结果。
定义
范数为
,
范数下的收敛阶为
。
算例4.1考虑如下一维非线性Allen-Cahn方程的初边值问题(IBVP(1.1)),取定初边值条件为
给定
,
。
在表1给出了取不同网格的步长的条件下,差分格式SP-DFFT-FDMS所得数值解
在
范数下的误差和收敛阶,从表格中,可以观察到数值解具有二阶收敛精度。

Table 1. The numerical result with different steps for Example 1 ( τ = h 2 / 2 ( ε 2 + 1 ) )
表1. 取不同步长时的数值结果
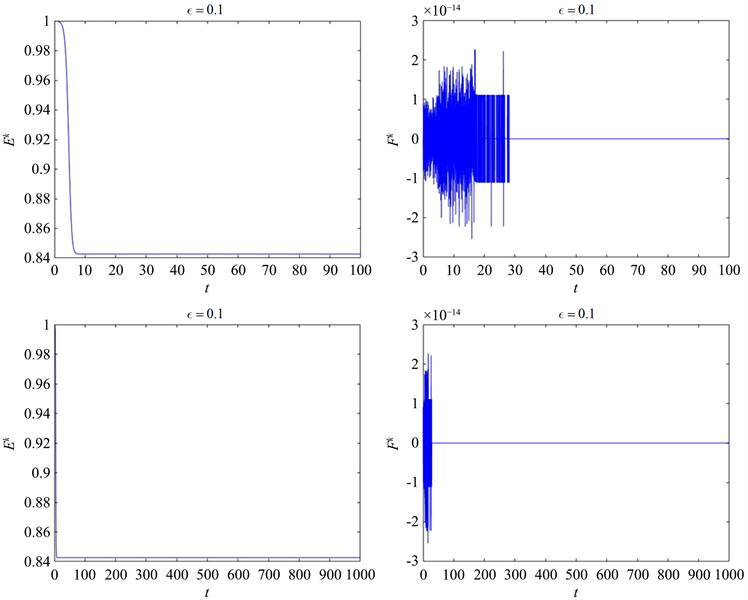
Figure 1. Time evolutions of Ek, Fk provided by SP-DFFT-FDMs with h = 0.1, C = 1
图1. 取h = 0.1, C = 1时,格式SP-DFFT-FDMs所得Ek, Fk的时间演化图

Figure 2. Time of evolution of
provided by SP-DFFT-FDMs with h = 0.1, C = 1
图2. 取h = 0.1, C = 1时,格式SP-DFFT-FDMs的最大值
图1表示离散能量
和
当时间
和
的演化过程,如图所见,离散能量
随时间推移而衰减,其中
均趋于零,达到机器精度,说明离散能量方程对机器精度有效。图2刻画了本文格式所得数值解的最大值,图2验证了差分格式满足离散的最大化原则。此外,由图1和图2可以看出,当
时,离散能量依旧满足衰减性且
趋于零,同时满足了最大化原则,这验证了差分格式长时间计算的有效性。
6. 结论
本文对一维非线性Allen-Cahn方程建立了一种无条件稳定的显式保结构算法。离散格式满足离散最大化原则且所得的数值解满足离散能量衰减性;通过离散最大化原则证明了该差分格式在
范数下的收敛阶达到二阶。第四节的数值算例验证了理论结果,此外,从数值结果来看,当
时,该格式仍保持离散最大化原则、能量稳定性以及二阶收敛,可见,本文所设计的保结构算法具有长时间模拟的优势。然而该格式应用于求解二维非线性Allen-Cahn方程时,能否满足离散最大化原则和离散能量稳定性有待进一步分析。
基金项目
国家自然科学基金项目(No. 11861047);江西省杰出青年基金(20212ACB211006);江西省自然科学基金(20202BABL201005)。