1. 引言
20世纪下半叶以来,非线性科学有了很大的发展。混沌是非线性科学的一个研究热点,被认为是继相对论和量子力学 [1] 之后的第三次革命。由于非线性振动在实际工程中的广泛存在,故而研究具有特殊动力学行为的混沌系统,对科学的进一步发展,解决实际工程中的问题,都具有很大的理论意义和科学价值。1963年,Lorenz在一个三维自治系统中首次发现了混沌吸引子。1999年,Chen等人也发现了和Lorenz系统相似但不同的混沌吸引子。近年来,随着学术界在 [2] [3] [4] [5] 中对于非线性对混沌现象的深入探索,混沌系统的动力学行为的变化及对混沌状态的控制已成为研究混沌的重要内容。
随着非线性科学的广泛应用,国内外的学者基于不同的策略提出了大量的混沌控制方法。Sharma等人 [6] 应用线性增强的方法来控制混沌系统吸引子的多态性。Feng和Wei等 [7] 研究了时滞反馈法对混沌系统的控制。Vaidyanathan [8] 对于超混沌系统通过自适应法进行系统的控制。Wei等人应用非线性反馈控制器、滑膜控制器及其组合来控制具有混沌特性的动力学系统。对于混沌系统来说,外力施加并输入时,系统将获得能量,所以,系统的动力响应也会受到系统能量的控制。如外部电磁辐射可以通过提供足够的能量来改变神经元 [9] 的电活动模式。对于非线性系统,我们可以从理论上来探讨其物理能量。Wang等人利用Helmholtz定理对无量纲动力系统的哈密顿能量进行了计算。Ma等人认为能量反馈可以有效抑制振荡。Guo等人提出相位压缩和能量调和来控制混沌系统。因此,讨论能量对于混沌系统的动力学行为控制是十分具有意义的。
本文通过对具有多个平衡点的混沌系统,在理论分析和数值仿真下,详细分析了系统的基本动力学特性。通过Helmholtz’s定理求出了系统的Hamilton函数,设计了相应的能量反馈控制器通过降低能量消耗来控制混沌系统。
2. 系统的动力学分析
2.1. 混沌系统的方程描述
对于以下系统:
(1)
这里
为系统参量,
为系统参数。
当
,初始状态
,仿真时间为
时,系统(1)生成一个混沌系统。此时系统的相图及时间序列图如图1所示。
 (a)
(a) 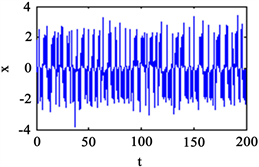 (b)
(b)
Figure 1. (a) Phase diagram; (b) Time series diagram
图1. (a) 相图;(b) 时间系列图
2.2. 系统的平衡点及稳定性
对于系统(1),我们令
,系统的平衡点为
,对于平衡点的稳定性,通过求得其Jacobian矩阵为
所以,特征多项式为
其中
,
,
计算行列式
由Routh-Hurwitz稳定判据知,系统在稳定点处的特征方程的所有特征值都具有负实部的充要条件是:
因此,当且仅当
成立,以上特征方程的所有特征值的实部一定是负数。当满足以上条件时,平衡点是稳定的,否则,不稳定。
2.3. 参数a的影响
系统(1)的参数分别取
,初始条件取为
,当a的取值范围为
时,关于a的分岔图如图2所示,观察参数a的分岔情况,可以看出,当
时,系统处在稳定状态,不存在混沌吸引子;在
时,所在区间分岔图无任何规律可循,此时系统处在混沌状态;当
时,系统明显处于五周期状态;而在越过
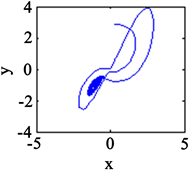
之后,系统又回到混沌状态。同时在上述区间段中,选取较为典型的参数值a,给出了系统(1)在x-y平面上的相图如图3所示。
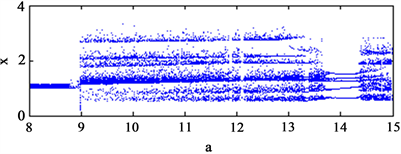
Figure 2. Bifurcation diagram of parameters a
图2. 关于参数a的分岔图
 (a)
(a) 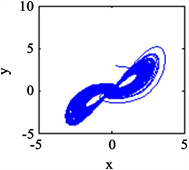 (b)
(b)  (c)
(c) 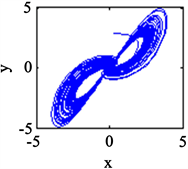 (d)
(d)
Figure 3. The phase diagram in the x-y plane increments with parameter a (a)
; (b)
; (c)
; (d)
图3. 随参数a逐步增大在x-y平面上的相图(a)
;(b)
;(c)
;(d)
3. 能量反馈控制
3.1. 系统的Hamilton函数
在这部分里,我们将寻找一个相空间变量函数,它就是系统(1)的Hamilton能量函数。这里,我们将系统(1)简记为
其中
,
是光滑函数。
由文献 [10] 知,
满足以下关系
这里
指涡旋场,
指梯度场。
能量的变化来自于电场的做功,
作为Hamilton能量,它满足以下方程:
则对于系统(1),可以得到
由上述关系,Hamilton能量函数
服从以下偏微分方程:
求解上式,有
(2)
同时,可以验证其微分系数与时间的关系:
3.2. 能量控制方案及数值结果
由式(2),可以看出,系统参数及变量的改变对Hamilton能量的影响很大,不同状态下,系统的能量函数也会发生巨大变化。相反,能量函数的改变也会对混沌系统的状态产生影响,故而,我们提出基于Hamilton能量函数的一种控制方法,设计控制器并将其引入混沌系统,其动力系统如下:
其中,H为系统的Hamilton能量函数,参数k是控制能量流的反馈增益。下面,我们将给定不同的反馈增益,来控制动力学系统,进而研究系统的状态变化。
通过固定参数
,选择不同的参数k来研究能量函数对混沌系统的抑制,结果如图所示。
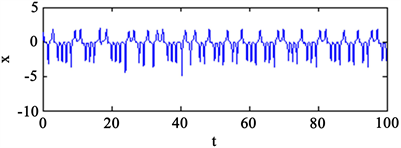
Figure 4. Time response diagram of variable x when feedback gain
图4. 反馈增益
时,变量x的时间响应图

Figure 5. Time response diagram of variable x when feedback gain
图5. 反馈增益
时,变量x的时间响应图
从图4可以直观看到,当选择反馈增益
时,系统未得到有效控制,在0~100 s内一直处于混沌状态;图5表明,当反馈增益
时,系统在经过短暂的无规则运动,即混沌状态后被有效的控制到一个平衡点上。
对比以上两种结果,可以看出通过改变反馈增益k的取值,能够有效改变系统的运动状态,从而达到控制系统状态演化的目标。能量的变化是动力学系统振荡的重要组成,基于Hamilton能量函数所设计的反馈法确实可以对已知的混沌系统进行一定程度的控制,通过改变反馈增益的大小,提供足够的能量使得系统能够快速脱离混沌,使系统有效的被控制在平衡点处。
4. 结论
本文对提出的具有多个平衡点的三维自激混沌系统,通过理论分析和数值仿真,讨论了系统平衡点的稳定性及随参数变化,系统的复杂动力学特性。同时基于Hamilton定理等,计算了系统的Hamilton能量,调整适当的参数,利用Helmholtz’s定理对Hamilton能量进行反馈控制,对处于混沌状态的系统进行控制,达到了理想的平衡态。对于此类特殊系统的研究,对如何有效消除和解决实际工程中出现的混沌振动问题,在理论和控制方法上,提供了良好的启示和借鉴。
NOTES
*通讯作者。