对称Max Plus半环上热带多项式的根

Roots of Tropical Polynomials over Symmetric Max-Plus Semiring

摘要: 多项式的求根是数学的核心内容之一。本文将讨论系数在热带对称max-plus半环S_max上的一元热带多项式根的存在性与求根公式。

Abstract: Finding roots of polynomials is one of the core contents of mathematics. In this paper, we discuss the existence and formula of roots of unitary tropical polynomials with coefficients on tropical symmetrized max-plus semiring S_max.

1. 引言

热带几何的研究始于1970年 [1]，它是一种建立在热带半环 ${ℝ}_{\max }$ 上的几何。热带半环是具有加法 $\oplus$ 和乘法 $\otimes$ 两种运算的集合 ${ℝ}_{\max }:=ℝ\cup \left\{-\infty \right\}$，详见定义1。

近些年来，人们试图在热带几何中建立一个“热带”线性代数，并进一步探究“经典”和“热带”世界之间的联系。虽然这一领域已经取得了一些发展和进步，但许多基本问题尚未得到解决。就目前的研究来看，热带几何常与代数、阶理论和离散数学相结合，例如在调度和优化、形式语言理论、数值分析和动力系统方面有广泛的应用 [2]。我们可以利用热带几何，以一种线性的、组合的方式来分析固有的非线性问题。例如将一个经典的非线性系统转换为一个分段的热带线性系统，然后利用热带线性代数的方法来反映关于原始系统的信息 [2]。这种方法已经被用于矩阵多项式特征值的计算 [3]，也可以用于理解离散事件动力系统 [4]。

为解决热带几何中加法的不可逆性，1990年M. Plus引入了对称max-plus半环 ${\mathbb{S}}_{\max }$ [5]，其中等式关系用“balance”关系来表示。M. Plus还介绍了一种消去法，进而推广了G. Minoux定理 [5]。 ${\mathbb{S}}_{\max }$ 是热带半环的推广，是对线性系统的一种拓展。随后在1992年，F. Baccelli对 ${\mathbb{S}}_{\max }$ 上多项式的因式分解、运算和矩阵的结构、线性方程组等问题进行了研究 [6]。1999年，S. Gaubert和P. Butkovic研究了在 ${\mathbb{S}}_{\max }$ 上的“Sign-nonsingular”矩阵 [7] 和“unbalanced”行列式矩阵 [8]，并分析了两种矩阵之间的关系。J. Norton和S. Spiroff在2018年讨论了热带半环的高维推广 [9]。C. G. Zonnefeld在 [10] 中研究了热带半环与有向图之间的相互作用。这使得热带几何的内容更加丰富。

本文将讨论对称max-plus半环 ${\mathbb{S}}_{\max }$ 上的一元多项式的根。具体而言，文章给出一元多项式根的存在性判定及求解的方法。本文的研究对 ${\mathbb{S}}_{\max }$ 上矩阵的特征值和特征向量研究有着重要的作用，并且丰富了热带多项式的研究内容。

文章结构如下：第二节介绍对称热带半环的基础运算(2.1, 2.2)，以及 ${\mathbb{S}}_{\max }$ 上多项式的一些定义与性质(2.3)。第三节将研究 ${ℝ}_{\max }$ 上多项式根的存在性(3.1)，并分析了与 ${\mathbb{S}}_{\max }$ 多项式之间的关系(3.2)。

2. 预备知识

2.1. 热带半环 ${ℝ}_{max}$

定义1 [11] 记 ${ℝ}_{\max }:=ℝ\cup \left\{-\infty \right\}$，对于任意 $a,b\in {ℝ}_{\max }$ 定义加法 $\oplus$ 和乘法 $\otimes$ 如下：

$a\oplus b:=\max \left\{a,b\right\}$,

$a\otimes b:=a+b$.

称 $\left({ℝ}_{\max },\oplus ,\otimes \right)$ 为热带半环。显然“0”是乘法单位元， $\epsilon :=-\infty$ 是加法零元。

让我们考虑基于Dioid结构 [10] 下的 ${ℝ}_{\max }^2$ 代数：

$\left(x^{\prime },x^{″}\right)\oplus \left(y^{\prime },y^{″}\right):=\left(x^{\prime }\oplus y^{\prime },x^{″}\oplus y^{″}\right)$,

$\left(x^{\prime },x^{″}\right)\otimes \left(y^{\prime },y^{″}\right)=\left(x^{\prime }{y}^{\prime }\oplus x^{″}{y}^{″},x^{\prime }{y}^{″}\oplus x^{″}{y}^{\prime }\right)$.

其中 $\left(x^{\prime },x^{″}\right),\left(y^{\prime },y^{″}\right)\in {ℝ}_{\max }^2$。显然 $\left(\epsilon ,\epsilon \right)$ 是零元， $\left(0,\epsilon \right)$ 是单位元。

定义2 [5] 设 $x=\left(x^{\prime },x^{″}\right)\in {ℝ}_{\max }^2$，定义

$\ominus x=\left(x^{″},x^{\prime }\right)$ ;

$\left|x\right|=x^{\prime }\oplus x^{″}$ ;

$x^{•}=\left(\left|x\right|,\left|x\right|\right)$.

设 $a,b\in {ℝ}_{\max }^2$ 定义： $a\ominus b=a\oplus \left(\ominus b\right)$。

性质1 [5] 对任意 $a,b\in {ℝ}_{\max }^2$， $a\ne b$，如下结论成立：

1) $a^{•}={\left(\ominus a\right)}^{•}$ ；

2) 幂等性： ${\left(a\right)}^{••}=a^{•}$ ；

3) 吸收性： $a\otimes b^{•}={\left(a\otimes b\right)}^{•}$ ；

4) 对合性： $\ominus \left(\ominus a\right)=a$ ；

5) $\ominus \left(a\oplus b\right)=\left(\ominus a\right)\oplus \left(\ominus b\right)$ ；

6) $\ominus \left(a\otimes b\right)=\left(\ominus a\right)\otimes b$ ；

7) $\left(\ominus a\right)\otimes \left(\ominus b\right)=a\otimes b$。

2.2. 对称Max-Plus半环 ${\mathbb{S}}_{max}$

定义3 [5] [ $\mathcal{R}$ 关系]设 $x=\left(x^{\prime },x^{″}\right),y=\left(y^{\prime },y^{″}\right)\in {ℝ}_{\max }^2$，定义

$x\mathcal{R}y\iff \{\begin{array}{l}{x}^{\prime }\oplus y^{″}=x^{″}\oplus y^{\prime },若x^{\prime }\ne x^{″}或y^{\prime }\ne y^{″},\\ \left(x^{\prime },x^{″}\right)=\left(y^{\prime },y^{″}\right),其他情况.\end{array}$

可以验证， $\mathcal{R}$ 关系是 ${ℝ}_{\max }^2$ 上的一种等价关系。

定义4 [5] 记 ${\mathbb{S}}_{\max }:={ℝ}_{\max }^2╱\mathcal{R}$ 称为对称max-plus半环。对 $a,b\in {ℝ}_{\max }^2$ 记 $\overline{\left(a,b\right)}$ 为 $\left(a,b\right)$ 所在的等价类。

性质2 [5] 对 $t\in {ℝ}_{\max }$ 如下结论成立：

$\overline{\left(t,\epsilon \right)}=\left\{\left(t,x^{″}\right);x^{″}<t\right\}$ ;

$\overline{\left(\epsilon ,t\right)}=\left\{\left(x^{\prime },t\right);x^{\prime }<t\right\}$ ;

$\overline{\left(t,t\right)}=\left\{t^{•}=\left(t,t\right)\right\}$.

记

${ℝ}_{\max }^{\oplus }=\left\{\overline{\left(t,\epsilon \right)}|t\in {ℝ}_{\max }\right\}$ ;

${ℝ}_{\max }^{\ominus }=\left\{\overline{\left(\epsilon ,t\right)}|t\in {ℝ}_{\max }\right\}$ ;

${ℝ}_{\max }^{•}=\left\{\overline{\left(t,t\right)}|t\in {ℝ}_{\max }\right\}$.

显然， ${\mathbb{S}}_{\max }={ℝ}_{\max }^{\oplus }\cup {ℝ}_{\max }^{\ominus }\cup {ℝ}_{\max }^{•}$， $\left\{\left(\epsilon ,\epsilon \right)\right\}={ℝ}_{\max }^{\oplus }\cap {ℝ}_{\max }^{\ominus }\cap {ℝ}_{\max }^{•}$。易验证，映射 ${ℝ}_{\max }\to {ℝ}_{\max }^{\oplus }$， $a=\overline{\left(a,-\infty \right)}$ 是一个半环同构。为方便起见，后文将不区分二者，即 ${ℝ}_{\max }^{\oplus }={ℝ}_{\max }$。进而 ${ℝ}_{\max }^{\ominus }=\ominus {ℝ}_{\max }$。特别地，对任意 $s\in {ℝ}_{\max }$，有 $\left|s\right|=\left|\ominus s\right|=\left|s^{•}\right|=s\in {ℝ}_{\max }$。直接验证可得如下引理：

引理1对任意 $a,b\in {\mathbb{S}}_{\max }$，如下结论成立：

1) $a\oplus b=\{\begin{array}{l}a,若\left|a\right|>\left|b\right|或a=b;\\ b,若\left|a\right|<\left|b\right|;\\ {\left|a\right|}^{•},若\left|a\right|=\left|b\right|且a\ne b.\end{array}$

2) $\left|a\oplus b\right|=\left|a\right|\oplus \left|b\right|$， $\left|a\otimes b\right|=\left|a\right|\otimes \left|b\right|$。

性质3 若 $a_1,\cdots ,a_n,c\in {\mathbb{S}}_{\max }$ 使得 $a_1\oplus \cdots \oplus a_n=c$ 则要么存在i，使得 $a_i=c$，要么存在 $j,k$，使得 $a_j\ne a_k$ 且 $a_j\oplus a_k=c\in {ℝ}_{\max }^{•}$。

证明 记 $I=\left\{a_i|\left|a_i\right|=\left|c\right|\right\}$。由引理1(2)知， $\left|c\right|=\text{max}\left\{\left|a_1\right|,\cdots ,\left|a_n\right|\right\}$，从而 $I\ne \varnothing$。若对任意 $x\in I$，都有 $x\ne c$，则由引理1(1)， $c\in {ℝ}_{\max }^{•}$，且存在 $j,k$，使得 $a_j\oplus a_k=c$。

2.3. ${\mathbb{S}}_{max}$ 上的多项式

定义5半环上的多项式为 $f\left(x\right)={\oplus }_{i=0}^n\left(a_i\otimes x^i\right)$，其中 $a_i\in {\mathbb{S}}_{\max },n\in \mathbb{N}$。全体 ${\mathbb{S}}_{\max }$ 上的一元多项式构成的集合记作 ${\mathbb{S}}_{\max }\left[x\right]$。类似地，定义 ${ℝ}_{\max }\left[x\right]=\left\{{\oplus }_{i=0}^n\left(a_i\otimes x^i\right)|a_i\in {ℝ}_{\max }\right\}$。

设 $f\left(x\right)={\oplus }_{i=0}^n\left(a_i\otimes x^i\right)\in {\mathbb{S}}_{\max }\left[x\right]$，令

$\left|f\left(x\right)\right|={\oplus }_{i=0}^n\left(\left|a_i\right|\otimes x^i\right)$, $f^{\pm }\left(x\right)={\oplus }_{i=0}^n\left(a_i^{\pm }\otimes x^i\right)$,

其中 $a_k^{+}=\{\begin{array}{l}{a}_k,a_k\in {ℝ}_{\max }\\ \epsilon ,a_k\in \ominus {ℝ}_{\max }\\ \left|a_k\right|,a_k\in {ℝ}_{\max }^{•}\end{array}$ ； $a_k^{-}=\{\begin{array}{l}\epsilon ,a_k\in {ℝ}_{\max }\\ \ominus a_k,a_k\in \ominus {ℝ}_{\max }\\ \left|a_k\right|,a_k\in {ℝ}_{\max }^{•}\end{array}$。

显然， $f^{\pm }\left(x\right)$ 是良好定义的，且被 $f\left(x\right)$ 唯一确定。根据定义，容易验证如下引理。

引理2

1) $f^{\pm }\left(x\right),\left|f\left(x\right)\right|\in {ℝ}_{\max }\left[x\right]$，

2) $f\left(x\right)=f^{+}\left(x\right)\ominus f^{-}\left(x\right)$， $\left|f\left(x\right)\right|=f^{+}\left(x\right)\oplus f^{-}\left(x\right)$。特别地，对任意 $a\in {\mathbb{S}}_{\max }$， $\left|f\left(a\right)\right|=f^{+}\left(\left|a\right|\right)\oplus f^{-}\left(\left|a\right|\right)$。

例1 设 $f\left(x\right)=7^{•}\otimes x^5\oplus 5\otimes x^4\ominus 5\otimes x^3\oplus 0^{•}\otimes x\ominus 1\in {\mathbb{S}}_{\max }\left[x\right]$，则 $f^{+}\left(x\right)=7\otimes x^5\oplus 5\otimes x^4\oplus x$， $f^{-}\left(x\right)=7\otimes x^5\oplus 5\otimes x^3\oplus x\oplus 1$。

性质4 若 $f\left(x\right)\in {\mathbb{S}}_{\max }\left[x\right]$，且 $\left|a\right|>\left|b\right|$ 使得 $\left|f\left(b\right)\right|>\left|a_0\right|$，则 $\left|f\left(a\right)\right|>\left|f\left(b\right)\right|$。

证明 对于 $f\left(x\right)$ 中任一项单项式 $a_n\otimes x^n$，由 $\left|a\right|>\left|b\right|$，知 $\left|a_n\otimes a^n\right|>\left|a_n\otimes b^n\right|$，则 $\left|{\oplus }_{k=1}^n{a}_k\otimes a^n\right|>\left|{\oplus }_{k=1}^n{a}_k\otimes b^n\right|$，故 $\left|f\left(a\right)\right|=\left|{\oplus }_{k=1}^n{a}_k\otimes a^n\right|>\left|f\left(b\right)\right|=\left|{\oplus }_{k=1}^n{a}_k\otimes b^n\right|$。

3. ${ℝ}_{max}$ 上多项式的解

如无特殊说明，本节总假设 $f\left(x\right)={\oplus }_{i=0}^n\left(a_i\otimes x^i\right)\in {ℝ}_{\max }\left[x\right]$， $t\in {ℝ}_{\max }$，并分别讨论 $f\left(x\right)=t$ 在 ${ℝ}_{\max }$ 和 ${\mathbb{S}}_{\max }$ 中的解。记

$r_o\left(f,t\right)=\text{min}\left\{t-a_1,\frac{t-a_3}{3},\cdots \right\}$,

$r_e\left(f,t\right)=\text{min}\left\{\frac{t-a_2}{2},\frac{t-a_4}{4},\cdots \right\}$,

分别简记 $r_o=r_o\left(f,t\right),r_e=r_e\left(f,t\right)$。令 $r=\min \left\{r_o,r_e\right\}$。

令 $f_o\left(x\right)=a_1\otimes x\oplus a_3\otimes x^3\oplus \cdots$， $f_e\left(x\right)=a_2\otimes x^2\oplus a_4\otimes x^4\oplus \cdots$。下面的引理可以直接验证。

引理3

1) $f\left(x\right)=f_o\left(x\right)\oplus f_e\left(x\right)\oplus a_0$ ；

2) $r_o$ 是方程 $f_o\left(x\right)=t$ 在 ${ℝ}_{\max }$ 上的唯一解；

3) $r_e$ 是方程 $f_e\left(x\right)=t$ 在 ${ℝ}_{\max }$ 上的唯一解；

4) 若 $r_o<r_e$，则 $t=f_o\left(r_o\right)>f_e\left(r_o\right)$ ；

5) 若 $r_o>r_e$，则 $t=f_o\left(r_o\right)>f_e\left(r_o\right)$ ；

6) $f_o\left(\ominus x_o\right)=\ominus f_o\left(x_o\right)$， $f_e\left(\ominus x_e\right)=f_e\left(x_e\right)$。

3.1. ${ℝ}_{max}$ 上多项式在 ${ℝ}_{max}$ 上的解

引理4 若 $f\left(x\right)=t$ 在 ${ℝ}_{\max }$ 中有解，则 $t\ge a_0$。

证明 设 $x=x_0$ 是方程的解，则 $t=f\left(x_0\right)=f_o\left(x_0\right)\oplus f_e\left(x_0\right)\oplus a_0\ge a_0$。

引理5 若 $t>a_0$，则 $f\left(x\right)=t$ 在 ${ℝ}_{\max }$ 中有唯一解 $\min \left\{r_o,r_e\right\}$。

证明 当 $t>a_0$ 时， $f\left(x\right)=t$ 与 $f_o\left(x\right)\oplus f_e\left(x\right)=t$ 同解。由引理3， $f_o\left(r\right)\oplus f_e\left(r\right)=t$。

若 $m>r$ 则存在k，使得 $m>\frac{t-a_k}{k}$， $f\left(m\right)>t$。

若 $m<r$，对于任意j，都有 $m<\frac{t-a_j}{j}$， $f\left(m\right)<t$。得证。

引理6 若 $t=a_0$ 则 $f\left(x\right)=t$ 在 ${ℝ}_{\max }$ 中有无穷多个解。进一步，全体解为 $\left\{x_0\in {ℝ}_{\max }|x_0\le r\right\}$。

证明 对任意 $x_0>r$， $f_o\left(x_0\right)\oplus f_e\left(x_0\right)>t$，从而 $f\left(x_0\right)>t$。

对任意 $x_0\le r$，由引理3(1)， $f\left(x_0\right)=a_0=t$。引理得证。

定理1 $f\left(x\right)=t$ 在 ${ℝ}_{\max }$ 中有解当且仅当 $t\ge a_0$。特别地，若 $t>a_0$ 则方程有唯一解 $x=r$ ；若 $t=a_0$，则方程有无穷解，全体解为 $\left\{x_0\in {ℝ}_{\max }|x_0\le r\right\}$。

3.2. ${ℝ}_{max}$ 上多项式在 ${\mathbb{S}}_{max}$ 上的解

引理7 若 $f\left(x\right)=t$ 在 ${\mathbb{S}}_{\max }$ 中有解，则 $t\ge a_0$。

证明 若 $x_0\in {\mathbb{S}}_{\max }$ 是 $f\left(x\right)=t$ 的解，则 $f\left(\left|x_0\right|\right)=\left|f\left(x_0\right)\right|=\left|t\right|=t$。由引理4， $t\ge a_0$。

性质5 若 $t>a_0$， $m\in {\mathbb{S}}_{\max }$ 是 $f\left(x\right)=t$ 的解，则 $\left|m\right|=r$，且 $m\notin {ℝ}_{\max }^{•}$。

证明 由引理2知， $\left|m\right|$ 是 $f\left(x\right)=t$ 的解。由引理5， $\left|m\right|=r$。若 $m\in {ℝ}_{\max }^{•}$，则 $f\left(m\right)\in {ℝ}_{\max }^{•}$。命题得证。

引理8 当 $t>a_0$ 时， $f\left(x\right)=t$ 有解。

1) 若 $r_o\le r_e$，则 $f\left(x\right)=t$ 在 ${\mathbb{S}}_{\max }$ 中有唯一解 $r_o$。

2) 若 $r_o>r_e$，则 $f\left(x\right)=t$ 只有两个解，分别为 $r_e$， $\ominus r_e$。

证明 1) 由定理1， $f\left(r_o\right)=t$。由引理3， $t=f_o\left(r_o\right)\ge f_e\left(r_o\right)$，且

$f\left(\ominus r_o\right)=f_o\left(\ominus r_o\right)\oplus f_e\left(\ominus r_o\right)=\left(\ominus t\right)\oplus f_e\left(r_o\right)=\ominus t$ 或 $t^{•}$。从而 $\ominus r_o$ 不是 $f\left(x\right)=t$ 的根。由性质5，(1)得证。

2) 类似地， $f\left(r_e\right)=f\left(\ominus r_e\right)=t$。由性质5，(2)得证。

性质6 若 $t=a_0$ 则 $f\left(x\right)=t$ 在 ${\mathbb{S}}_{\max }$ 中有无穷多个解。全体解为。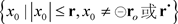

证明 由性质5，若 $x_0\in {\mathbb{S}}_{\max }$ 是 $f\left(x\right)=t$ 的解，则 $\left|x_0\right|\le r$。由于 $f\left(\left|x_0\right|\right)=f_o\left(\left|x_0\right|\right)\oplus f_e\left(\left|x_0\right|\right)\oplus a_0$，

当 $x_0=r$ 时， $f_o\left(x_0\right)\oplus f_e\left(x_0\right)=t,f\left(x_0\right)=f\left(r\right)=t\oplus t=t$。

当 $x_0=\ominus r=\ominus r_e$ 时， $f_o\left(x_0\right)\oplus f_e\left(x_0\right)=t,f\left(x_0\right)=f\left(\ominus r_e\right)=t$。

当 $x_0=\ominus r=\ominus r_o$ 时， $f_o\left(x_0\right)\oplus f_e\left(x_0\right)=\ominus t,f\left(x_0\right)=f\left(\ominus r_o\right)=t^{•}$。

当 $x_0=\ominus r=\ominus r_o=\ominus r_e$ 时， $f\left(x_0\right)=t^{•}$。

当 $x_0=r^{•}$ 时， $f\left(x_0\right)=f\left(r^{•}\right)=t^{•}\oplus t=t^{•}$。

当 $\left|x_0\right|<r$ 时，由性质4， $f_o\left(\left|x_0\right|\right)\oplus f_e\left(\left|x_0\right|\right)<f_o\left(r\right)\oplus f_e\left(r\right)=t$。进而 $f\left(\left|x_0\right|\right)=f_o\left(\left|x_0\right|\right)\oplus f_e\left(\left|x_0\right|\right)\oplus t=t$。

综上所述，原方程有无穷解。

定理2 $f\left(x\right)=t$ 在 ${\mathbb{S}}_{\max }$ 中有解当且仅当 $t\ge a_0$。特别地，当 $t>a_0$ 时，若 $r_o\le r_e$，方程有唯一解 $r_o$ ；若 $r_o>r_e$ 方程只有两个解 $r_e,\ominus r_e$ ；当 $t=a_0$ 时，方程有无穷解，全体解为。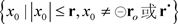

基金项目

NSF of Yunnan Provincial Department of Education (No. 2020J0375).