一道中考题的解法赏析

Appreciation of the Solution of a Question of Senior High School Entrance Examination

摘要: 利用“截长补短”、旋转等方法构造全等三角形、平行四边形以及相似三角形得到了黔东南州2021年一道中考题的九种证明方法。

Abstract: The nine proof methods of a question of senior high school entrance examination in Qiandongnan 2021 were obtained by using methods such as “taking from the long to add to the short” and rota-tion to construct congruent triangles, parallelograms, and similar triangles.

1. 引言

“截长补短”法中的“截长”是指在较长的线段上截取一条线段，使之等于已知的较短的线段；“补短”是指延长较短的线段，使之等于较长的线段 [1]。在初中的几何题中，“截长补短”法常用于证明三角形全等 [2] 或证明线段和差问题 [3] [4]。在线段和差问题中，常构造全等三角形，用三角形全等的性质，最终求得线段的和差关系 [5]。用“截长补短”法解几何题，这其中也会运用到旋转思想 [6] 以及等边三角形的判定和性质 [7]。在具体问题中运用此方法，需要结合已知条件，灵活的运用特殊三角形、特殊四边形的判定和性质以及图形的旋转。

“截长补短”法对学生来说并不陌生，但是学生在遇到线段和差的具体问题中常被如何“截长”，如何“补短”所困扰。贵州省黔东南州2021年中考数学试题第25题(2) ① 问考查的是线段求和问题，文章运用“截长补短”法与旋转思想，不仅构造了全等三角形，还构造了平行四边形和相似三角形，利用其性质求证该题，最终得到了该题的九种证明方法。不同的证明方法用到了初中“图形与几何”部分的不同知识点，且各种解法步骤相对均衡。该题一题多解，有助于学生在这一个题中更好地复习相应知识点，同时提高学生灵活运用“截长补短”法解决问题的能力，笔者认为该题为一个好的数学问题，值得介绍分享。

2. 试题呈现

题目(2021年贵州·黔东南州卷)在四边形ABCD中，对角线AC平分 $\angle BAD$。

[探究发现]

(1) 如图1，若 $\angle BAD=120˚$， $\angle ABC=\angle ADC=90˚$。

求证： $AD+AB=AC$ ；

[拓展迁移]

(2) 如图2，若 $\angle BAD=120˚$， $\angle ABC+\angle ADC=180˚$。

① 猜想AB、AD、AC三条线段的数量关系，并说明理由；

② 若 $AC=10$，求四边形ABCD的面积。

Figure 1. Question (1)

图1. 问题(1)

Figure 2. Question (2)

图2. 问题(2)

3. 猜想结论

第(1)问根据已知条件比较容易得证 $AC=AD+AB$，这里不做讨论。第(2)问的①是猜想线段AB、AD、AC之间的数量关系并证明结论。猜想第(2)题中线段AB、AD、AC之间的数量关系时，学生可以借助第(1)问所得结论，猜想 $AC=AD+AB$，然后进行严格证明。该小题解决了，第(2)问的②小题也就随之求出。

4. 解法赏析

4.1. 用“截长补短”法 [3] [8] [9] 与旋转思想 [6]，构造全等三角形，用全等三角形的性质证明

Figure 3. Construction of congruent triangles by method of adding the short

图3. 补短法构造全等三角形

证法1：如图3，要证 $AC=AD+AB$，延长线段AD至点E，使得 $AE=AC$，只需证 $AB=DE$ 即可。连接EC，要证 $AB=DE$，只需证 $\Delta ABC$ 与 $\Delta EDC$ 全等。

延长AD至点E，使得 $AE=AC$，连接EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle DAC=\angle BAC=60˚$。

所以 $\Delta ACE$ 为等边三角形。

所以 $\angle E=60˚$。

因为 $\angle ABC+\angle ADC=180˚$，

所以 $\angle ACD+\angle BCA=60˚$。

又因为 $\angle ACD+\angle DCE=60˚$，

所以 $\angle BCA=\angle DCE$。

在 $\Delta ABC$ 和 $\Delta EDC$ 中，

$\{\begin{array}{l}\angle BAC=\angle E\\ AC=EC\\ \angle BCA=\angle DCE\end{array}$

所以 $\Delta ABC$ ≌ $\Delta EDC$。

所以 $AB=DE$。

所以 $AC=AD+AB$。

Figure 4. Construction of congruent triangles by the method of adding the short

图4. 补短法构造全等三角形

证法2：如图4，要证 $AC=AD+AB$，延长线段AB至点E，使得 $AC=AE$，只需证 $AD=BE$ 即可。连接EC，要证 $AD=BE$，只需证 $\Delta ADC$ 与 $\Delta EBC$ 全等。

延长AB至点E，使 $AE=AC$，连接EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle DAC=\angle BAC=60˚$。

所以 $\Delta AEC$ 为等边三角形。

所以 $\angle E=60˚$。

因为 $\angle ABC+\angle ADC=180˚$，

所以 $\angle BCA+\angle ACD=60˚$。

因为 $\angle BCA+\angle ECB=60˚$，

所以 $\angle ACD=\angle ECB$。

在 $\Delta ADC$ 和 $\Delta EBC$ 中，

$\{\begin{array}{l}\angle DAC=\angle E\\ AC=EC\\ \angle ACD=\angle ECB\end{array}$

所以 $\Delta ADC$ ≌ $\Delta EBC$。

所以 $AD=BE$。

所以 $AC=AD+AB$。

Figure 5. Construction of congruent triangles by method of cutting the long

图5. 截长法构造全等三角形

证法3：如图5，要证 $AC=AD+AB$，在线段AC上截取 $AF=AB$，只需证 $AD=FC$ 即可。要证 $AD=FC$，可构造一个 $\Delta CFE$，只需证 $\Delta ADC$ 与 $\Delta CFE$ 全等。

延长AB至点E，使得 $AE=AC$。

在AC上截取 $AF=AB$，连接EF、EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle BAC=60˚$。

易证 $\Delta AFE$ ≌ $\Delta ABC$，

所以 $\angle AFE=\angle ABC$。

所以 $\angle EFC={180}^{\circ }-\angle ABC$。

又因为 $\angle ADC+\angle ABC=180˚$，

所以 $\angle EFC=\angle ADC$。

因为 $AE=AC$，所以 $\Delta AEC$ 为等边三角形。

所以 $\angle ACE=60˚$。

在 $\Delta ADC$ 和 $\Delta CFE$ 中，

$\{\begin{array}{l}\angle ADC=\angle CFE\\ \angle DAC=\angle FCE\\ AC=CE\end{array}$

所以 $\Delta ADC$ ≌ $\Delta CFE$。

所以 $AD=CF$。

所以 $AC=AD+AB$。

Figure 6. Construction of congruent triangles by method of cutting the long

图6. 截长法构造全等三角形

证法4：如图6，要证 $AC=AD+AB$，在线段AC上截取 $AF=AD$，只需证 $AB=FC$ 即可。要证 $AB=FC$，可构造一个 $\Delta CEF$，只需证 $\Delta ACB$ 与 $\Delta CEF$ 全等。

延长AD至点E，使得 $AE=AC$。

在AC上截取 $AF=AD$，连接EF、EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle DAC=60˚$。

易证 $\Delta AFE$ ≌ $\Delta ADC$。

所以 $\angle AFE=\angle ADC$。

所以 $\angle EFC={180}^{\circ }-\angle ADC$。

又因为 $\angle ADC+\angle ABC=180˚$，

所以 $\angle EFC=\angle ABC$。

因为 $AE=AC$，所以 $\Delta AEC$ 为等边三角形。

所以 $\angle ACE=60˚$。

在 $\Delta ACB$ 和 $\Delta CEF$ 中，

$\{\begin{array}{l}\angle BAC=\angle FCE\\ \angle CBA=\angle EFC\\ AC=CE\end{array}$

所以 $\Delta ACB$ ≌ $\Delta CEF$。

所以 $AB=FC$。

所以 $AC=AD+AB$。

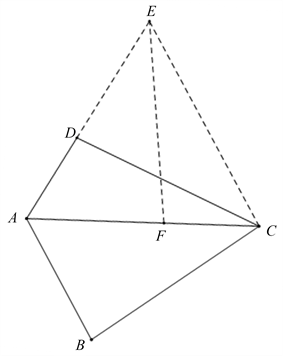
Figure 7. Rotation method for constructing congruent triangles

图7. 旋转法构造全等三角形

证法5：如图7，要证 $AC=AD+AB$，将 $\Delta ABC$ 绕点A逆时针旋转60˚，得到 $\Delta AFE$，由已知条件及旋转可知， $\Delta AFE$ 的边AF落在线段AC上，只需证 $AD=FC$ 即可。连接EC，要证 $AD=FC$，只需证 $\Delta DAC$ 与 $\Delta FCE$ 全等。

将 $\Delta ABC$ 绕点A逆时针旋转60˚，得到 $\Delta AFE$，连接EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle BAC=\angle CAD=60˚$。

所以 $\Delta AFE$ 的边AF落在线段AC上，边AE落在线段AD的延长线上。

因为 $AC=AE$，

所以 $\Delta ACE$ 是等边三角形。

所以 $\angle AEF+\angle FEC=60˚$， $CE=AC$。

因为 $\angle ACB+\angle ACD=60˚$，

由旋转可知 $\angle AEF=\angle ACB$，

所以 $\angle CEF=\angle ACD$。

在 $\Delta DAC$ 和 $\Delta FCE$ 中，

$\{\begin{array}{l}\angle DAC=\angle FCE\\ AC=CE\\ \angle ACD=\angle CEF\end{array}$

所以 $\Delta DAC$ ≌ $\Delta FCE$。

所以 $AD=CF$。

所以 $AC=AD+AB$。

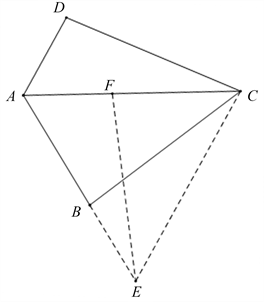
Figure 8. Rotation method for constructing congruent triangles

图8. 旋转法构造全等三角形

证法6：如图8，要证 $AC=AD+AB$，将 $\Delta ADC$ 绕点A顺时针旋转60˚，得到 $\Delta AFE$，由已知条件及旋转可知， $\Delta AFE$ 的边AF落在线段AC上，只需证 $AB=FC$ 即可。连接EC，要证 $AB=FC$，只需证 $\Delta ABC$ 与 $\Delta CFE$ 全等。

将 $\Delta ADC$ 绕点A顺时针旋转60˚，得到 $\Delta AFE$，连接EC。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle BAC=\angle CAD=60˚$。

所以 $\Delta AFE$ 的边AF落在线段AC上，边AE落在线段AB的延长线上。

因为 $AE=AC$，

所以 $\Delta AEC$ 为等边三角形。

所以 $\angle AEF+\angle FEC=60˚$， $CE=AC$。

因为 $\angle BCA+\angle ACD=60˚$，

由旋转可知： $\angle AEF=\angle ACD$，

所以 $\angle FEC=\angle BCA$。

在 $\Delta ABC$ 和 $\Delta CFE$ 中，

$\{\begin{array}{l}\angle BAC=\angle FCE\\ \angle BCA=\angle FEC\\ AC=CE\end{array}$

所以 $\Delta ABC$ ≌ $\Delta CFE$。

所以 $AB=FC$。

所以 $AC=AD+AB$。

4.2. 构造平行四边形，用平行四边形的性质证明

证法7：如图9，将 $\Delta ABC$ 绕点A顺时针旋转60˚，得到 $\Delta A{B}^{\prime }{C}^{\prime }$，由已知条件及旋转可知， $\Delta A{B}^{\prime }{C}^{\prime }$ 的边 $A{B}^{\prime }$ 在线段DA的延长线上，要证 $AC=AD+AB$，只需证 $D{B}^{\prime }=AC$。连接 $C{C}^{\prime }$，易证 $C{C}^{\prime }=AC$，则只需证 $D{B}^{\prime }=C{C}^{\prime }$。要证 $D{B}^{\prime }=C{C}^{\prime }$，只需证四边形 $B^{\prime }{C}^{\prime }CD$ 是平行四边形即可。

Figure 9. Constructing a parallelogram

图9. 构造平行四边形

将 $\Delta ABC$ 绕点A顺时针旋转60˚，得到 $\Delta A{B}^{\prime }{C}^{\prime }$，连接 $C{C}^{\prime }$。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $A{B}^{\prime }$ 在线段DA的延长线上。

所以 $\angle CA{C}^{\prime }=60˚$。

所以 $\Delta CA{C}^{\prime }$ 为等边三角形。

所以 $C{C}^{\prime }=AC$， $\angle C{C}^{\prime }A=60˚$。

由旋转可知： $\angle C^{\prime }A{B}^{\prime }=\angle CA{C}^{\prime }=60˚$，

$\angle A{B}^{\prime }{C}^{\prime }=\angle ABC$， $A{B}^{\prime }=AB$。

所以 $D{B}^{\prime }\parallel C{C}^{\prime }$。

又因为 $\angle ABC+\angle ADC=180˚$，

所以 $\angle A{B}^{\prime }{C}^{\prime }+\angle ADC=180˚$。

所以 $DC\parallel B^{\prime }{C}^{\prime }$。

所以四边形 $B^{\prime }{C}^{\prime }CD$ 是平行四边形。

所以 $D{B}^{\prime }=C{C}^{\prime }$。

所以 $AC=AD+AB$。

Figure 10. Constructing a parallelogram

图10. 构造平行四边形

证法8：如图10，将 $\Delta ADC$ 绕点A逆时针旋转60˚，得到 $\Delta A{D}^{\prime }{C}^{\prime }$，由已知条件及旋转可知， $\Delta A{D}^{\prime }{C}^{\prime }$ 的边 $A{D}^{\prime }$ 在线段BA的延长线上，要证 $AC=AD+AB$，只需证 $D^{\prime }B=AC$。连接 $C{C}^{\prime }$，易证 $C^{\prime }C=AC$，则只需证 $D^{\prime }B=C^{\prime }C$。要证 $D^{\prime }B=C^{\prime }C$，只需证四边形 $BC{C}^{\prime }{D}^{\prime }$ 是平行四边形即可。

将 $\Delta ADC$ 绕点A逆时针旋转60˚，得到 $\Delta A{D}^{\prime }{C}^{\prime }$，连接 $C{C}^{\prime }$。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $A{D}^{\prime }$ 在线段BA延长线上。

所以 $\angle CA{C}^{\prime }=60˚$。

所以 $\Delta CA{C}^{\prime }$ 为等边三角形。

所以 $C{C}^{\prime }=AC$， $\angle C{C}^{\prime }A=60˚$。

由旋转可知： $\angle C^{\prime }A{D}^{\prime }=\angle CA{C}^{\prime }=60˚$，

$\angle A{D}^{\prime }{C}^{\prime }=\angle ADC$， $A{D}^{\prime }=AD$。

所以 $D^{\prime }B\parallel C^{\prime }C$。

又因为 $\angle ABC+\angle ADC=180˚$，

所以 $\angle ABC+\angle A{D}^{\prime }{C}^{\prime }=180˚$。

所以 $D^{\prime }{C}^{\prime }\parallel BC$。

所以四边形 $BC{C}^{\prime }{D}^{\prime }$ 是平行四边形。

所以 $D^{\prime }B=C^{\prime }C$。

所以 $AC=AD+AB$。

4.3. 构造相似三角形，用相似三角形的性质证明 [10]

Figure 11. Constructing similar triangles

图11. 构造相似三角形

证法9：如图11，在线段AC上分别截取 $AE=AD$ 、 $AF=AB$，连接DE、BF。易证 $\Delta DEC$ ∽ $\Delta CFB$，由相似三角形的性质可知 $\frac{DE}{CF}=\frac{EC}{FB}$，分别用AD、 $AC-AB$ 、 $AC-AD$ 及AB代换DE、CF、EC及FB，就能证明 $AC=AB+AD$。

在线段AC上分别截取 $AE=AD$ 、 $AF=AB$。连接DE、BF。

因为AC平分 $\angle BAD$ 且 $\angle BAD=120˚$，

所以 $\angle BAC=\angle CAD=60˚$。

所以 $\Delta ADE$ 、 $\Delta ABF$ 均为等边三角形。

所以 $DE=AE=AD$， $BF=AF=AB$。

所以 $\angle DEC=\angle CFB=120˚$。

因为 $\angle ECD+\angle FCB=60˚$，

又因为 $\angle ECD+\angle EDC=60˚$，

所以 $\angle EDC=\angle FCB$。

所以 $\Delta DEC$ ∽ $\Delta CFB$。

所以 $\frac{DE}{CF}=\frac{EC}{FB}$。

因为 $CF=AC-AF=AC-AB$，

因为 $EC=AC-AE=AC-AD$，

所以 $\frac{AD}{AC-AB}=\frac{AC-AD}{AB}$。

所以 $AD\cdot AB=\left(AC-AD\right)\cdot \left(AC-AB\right)$。

$A{C}^2=AC\cdot AB+AC\cdot AD$，

$AC=AB+AD$。

5. 小结

上述的几种证法用到了等边三角形的判定及性质、全等三角形的判定及性质、平行四边形的判定及性质以及相似三角形的判定及性质；还使用了“截长补短”、添加辅助线、图形旋转等技巧。这种问题，不仅能将学生所学的这些知识联系起来，同时还能培养学生的发散思维，提高分析问题和解决问题的能力。这也为用“截长补短”法去证明线段和差问题提供了另一个思路，根据题目的已知条件，除了能用该方法构造全等三角形外，能否构造特殊几何图形去证明线段的和差呢？例如特殊四边形、相似三角形。

一个好的数学问题应该在知识内容上具有广泛的关联性，在解法上拥有多维度的探索性，在情感态度上能激发学生兴趣和形成对数学灵活性的观念。

致谢

非常感谢审稿人对本文提出宝贵的意见。