1. 引言
簇的维数是代数几何中的一个基本概念,簇的一种刻画.但是计算一个簇的维数是比较困难的,其中计算由单项式理想定义的簇的维数是比较简单的。D. Cox等人在 [1] 中,总结了一种计算由单项式理想定义的簇的维数的方法。J. Herzog在 [2] 的第二部分中介绍了希尔伯特函数,可以用来计算簇的维数。K. Hulek在 [3] 中介绍了希尔伯特零点定理、克鲁尔维数的概念。这篇文章总结文献 [1] [2] [3] 中提到由单项式理想定义的簇的维数问题,并且介绍一种算法,用来计算由单项式理想定义的簇的维数。最后利用maple实现程序,并且通过实例论证整个过程是可以用计算机软件实现。
2. 基础知识
我们定义数域k上的n维仿射空间为:
.
定义1:设子集
,那么X生成的消失理想如下:
.
可以证明上述定义的
为
中的一个理想。
定义2:设
是在数域k的n个元多项式环,对于环中的一个子集J,定义由J生成的簇(代数集):
.
根据上面的定义以及希尔伯特零点定理 [3],可以在
中的理想与
中子集定义出一个映射。那么在这个映射下,
中的素理想与
不可约簇是一一对应的 [4]。
定理1:假设
和
是
中的理想,
和
是
中
的仿射簇,那么两个簇的交集和并集也是簇,并且
,
.
定理2:假设簇X非空,其对应的消去理想是
,那么X是不可约簇当且仅当
是素理想。
其中不可约簇是指不存在
,其中
,
是X的两个真子集,
素理想是指,若
,那么必有
或
成立。
根据文献4定理3.9在
中素谱的诺特性质,和素理想和不可约簇的对应关系,可以证
明每个由不可约簇构成的降链具有有限长度。就像计算线性空间的维数一样。这里将降链的最大长度定义为簇的维数。
定义3:一个簇V的克鲁尔维数(krull)是V的最长降链的长度krdim
。其中降链是
.
根据上述定义,计算簇的维数要找到一条最长不可约簇的降链。利用
中的素理想与
中的不可约簇之间的对应关系,我们可以将上述问题转化为寻找最长素理想构成的降链的问题。
定义4:假设
是
中的一个单项式理想,那么
中的每一个生成元
都是单项式。
由于计算一般簇的维数是比较困难的,下面本文考虑一类由单项式理想的定义的簇。
3. 单项式理想所定义的簇维数
由于单项式中的任意非零次数的变量取零时,单项式就会为零。所以单项式理想的簇我们只需要考虑由类似坐标超平面来构成的。如下例所示:
例1:假设在
中有一个单项式理想
,那么:
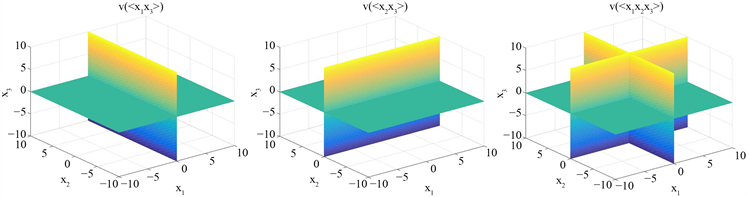
簇
,簇
,簇
如下图:
三个簇取交集不难看出是:
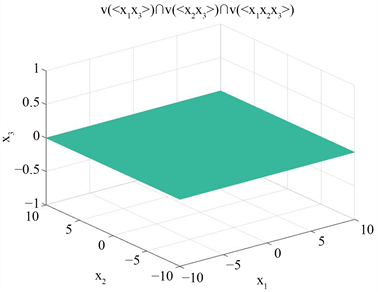
上面这个平面计算克鲁尔维数,先找到最长一条由不可约簇构成的链:
.
表示
点,
表示
其中
。
表示
其中
,也就是上面的平面。在这个
中最长可以找到由三个不可约簇构成的降链。根据克鲁尔维数的定义可知:
.
与之相对的素理想链:
.
受上例启发,可以将上述过程简化为计算理想中最小公共变量集的元素个数,一般的簇并不能做到这点。
定理3:设单项式理想
,那么单项式理想的簇
的维数和理想I公共变量有下述关系:
,
其中
是在单项式理想I中出现的公共变量。
证明:设
,那么
其中
是在单项式理想I中出现的公共变量。
根据定理6,把例5改成寻找公共变量集,
.
公共变量集合为:
,
其中最少的是
,个数为1。那么该簇的维数就等于:
.
4. 单项式理想簇的维数程序实现
根据上面的寻找最小公共变量集的做法,这里设计一种maple程序。先将全部的变元取出来,根据choose算法,做成公共变量集合,最后找到其中变元最少的。
用变量做成字符串,求全部子集。然后按照子集中元素的个数排列,将元素个数少的子集排在前面。choose算法如下:
下面是利用maple执行上述算法得出的结果。
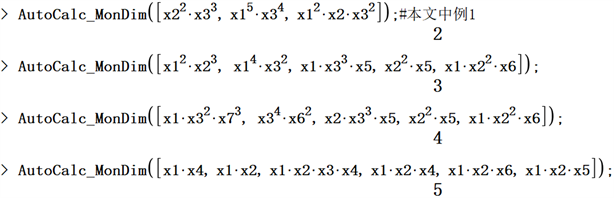
后面两个例子直接计算的话是比较复杂的。上面的几个例子可以看出到,利用maple执行上诉算法的程序,可以快捷有效的计算出一个由单项式定义的簇的维数。这里choose算法中对数据的处理会按照2n增加,本质上求理想中最少公共变量集的元素个数这一做法是不需要choose算法中全部的结果。如果可以精准的找到最少公共变量集,是可以对效率有很大的提升。