1. 引言
随着当今生产生活中人们对无人机、机器人、UAV等产品的要求不断提高,路径规划也成为了当今的研究热点。涉及有关路径规划的算法,可以大致分成两大类:传统算法 [1],人工势场算法、蚁群算法、A*算法等;智能算法 [2],如遗传算法、神经网络等。智能算法通常需要大量的迭代计算,收敛速度较慢,且易于陷入局部最优。上述传统的路径规划算法较为复杂,在处理低维空间的路径规划上体现出一定的优越性,但是在实际运用中,随着维度的增高,缺陷明显:表达构建空间需占用大量计算资源。而基于采样思想的规划算法,RRT (Rapid-exploration Random Tree)快速扩展随机树,无需对环境进行建模且适合高维空间。此类算法在无人机、机械臂等高维空间上体现出明显优势 [3]。
RRT算法是Steven M. LaValle教授提出的,它是一类基于采样的增量式搜索 [4] 规划算法。该算法无需建立空间信息模型,以随机采样的方式在任务空间中均匀采样,因此具有概率完备性 [5],相比其他算法可以适用于任意维度,任意环境,适用度更高。但是传统的RRT算法也存在扩展方向无目的性,易产生大量冗余点,收敛速度慢等问题。针对上述问题,众多学者提出了不同的改进方法。为了减少RRT随机搜索的范围,有人提出了目标偏向的采样策略,采用启发式搜索计算节点偏置概率 [6];或者加入目标引力来提高采样点的偏置率 [7]。但是以上改进算法都无法满足高实时性的要求。
针对RRT算法本身的不足,James J. Kuffner,Jr等人基于双向搜索的思想,提出双向随机扩展算法(bidirectional RRT)简称BI-RRT算法 [8]。该算法基于传统RRT,分别以起始点和目标点为初始点进行随机扩展树,直到两棵树的最新节点靠近或相遇,最后构建出完整的扩展树,相较传统RRT大大提高了收敛速度。虽然整体提高了搜索效率,但是每棵扩展树的扩展速度依然受到存在传统RRT算法均匀采样的弊端影响。在BI-RRT算法扩展中加入贪心思想,进而提出了RRT-Connect算法 [9]。张顺 [10] 等人将人工势场法加入RRT-Connect算法中,提出改进算法(PRRT-Connect),通过扩展函数,使得该算法在扩展过程中具有较强的方向性,修剪并平滑了路径,解决了无人机在复杂环境下的航线问题。但是这些算法中都存在参数设置不当,收敛速度缓慢问题。
为了解决BI-RRT算法中扩展目标方向性差、收敛速度缓慢的问题,提出一种新的改进采样点偏向目标(Sampling points are biased towards the target)的双向RRT算法,简称STB-RRT算法。该算法基于BI-RRT算法,通过起始点以及目标点同时生成随机树,利用偏向策略进行处理采样点使其偏向目标,再加入冗余的点删除,解决传统BI-RRT算法收敛速度缓慢的问题。
2. 基本BI-RRT算法
BI-RRT (双向快速扩展随机树)算法是在RRT算法基础上发展而成的,一种可在多维空间高效进行路径规划的算法。相比与其他算法复杂度小,可直接应用于非完整约束系统。该算法中,定义了两颗生长树Ta和Tb,Ta树以Qstart作为树根进行扩展,Tb树以Qgoal作为树根进行扩展,d为扩展步长,空间中任意节点为Qrand,扩展时任意一棵树中距离Qrand最近的点为Qnear,新节点为Qnew。在搜索空间中,两颗扩展树同时生成随机扩展节点Qrand,然后在已有随机树节点中找到距离Qrand较近的Qnear,在Qnear上向Qrand延申步长d获取新节点,之后通过对新节点Qnew进行检测,若有碰撞则删除该节点,若无碰撞则添加到随机树中。此时新节点Qnew的父节点是Qnear,依次方式进行扩展。当Ta和Tb树的最新节点Qnew的距离小于步长d时,可认为两颗生长树连接成功。图1表示该随机树的扩展过程。
3. 改进BI-RRT算法
BI-RRT算法最大的弊端就是两颗扩展树的扩展方向呈无目标性以及路径中冗余节点,本文通过扩展树同时采用采样点偏向目标策略,再结合冗余点删除策略,提高收敛速度,进而改进BI-RRT算法。
3.1. 采样点目标偏向算法
STB-RRT算法的改进策略是基于渐进最优性的思想:在扩展树采样以后,立即对其采样点进行偏向处理。详细的改进策略思路是:对扩展树中生成的Qrand做偏向处理,处理公式如下。
(1)
式中μ是调节系数,Qstart和Qgoal分别为起始节点和目标节点
表示起始点与目标点之间的欧氏距离。依据公式可知,经公式处理后的节点,其与目标点之间的欧氏距离有所减少。调节系数μ以及采样节点Qrand与目标节点Qgoal之间的距离可以决定减少量。当步长与目标偏向的距离差距过大时,调节系数μ的存在可使其策略不失效;当Qrand逼近目标点Qgoal,系数μ的影响也在变小。STB-RRT算法可以使两棵树同时趋向目标点,还可以保持单颗扩展树的扩展能力。
STB-RRT算法单颗树扩展过程如下图2所示。
图2中,Q1rand是未经过公式处理的采样点,Q1new和Q1near是未经过公式处理而得到的距离最近点与新节点。根据示意图可看出,STB-RRT算法中的改进策略使扩展树中父节点的选取比传统算法易发生变化,离目标节点近的点更易得到扩展。即使父节点的选取经处理后没有发生变化,新生节点也会因偏向目标处理更接近目标点。在扩展的过程中,保证了渐进最优性。因此STB-RRT算法可以使双向扩展更具有偏向目标的启发式效果,大大提高规划效率。
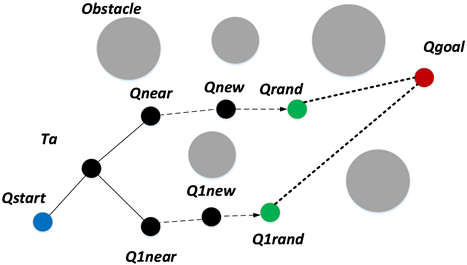
Figure 2. STB-RRT single tree expansion strategy diagram
图2. STB-RRT单棵扩展策略图
3.2. 修剪扩展树
在随机树扩展过程中,在一定范围内也会出现图3所示的冗余节点问题。例如当节点扩展到某段中时,Q1是父节点,此时由Q2向外扩展多个新节点Q3、Q4、Q5…,这些新节点之间的欧式距离较近,在一定空间下可能扩展出等效节点,如图3中的Q4和Q5扩展出等效节点,那么这些即为冗余点。冗余点的出现会耗费计算资源,影响算法的收敛速度。
出现该冗余节点的原因是新生节点之间距离较近。为了衡量每两个节点之间的距离,可以采用夹角θ表示。通过设置θ阈值,实现删除冗余节点的目的。当夹角小于或等于阈值时,极易出现冗余节点,及时删除该冗余点,可预防后续生成更多,减小数据量,节省计算资源可有效提高收敛速度;当夹角大于阈值时,可根据目标偏向采样点作进一步处理。
3.3. 算法实现
本文所提出改进BI-RRT算法的伪代码如STB-RRT算法所示:
1) Ta(Qstart);Tb(Qgoal)
2) For k=1 to N do
3) Qrand1←RANDOM-STATE();
4) Qrand2←RANDOM-STATE();
5) Qrand1←ADJUST-STATE(Qrand1);
6) Qnear←NEARST-NEIGHBOR(Qrand,T)
7) μ←SELECT(Qrand1,Qnear1);
8) Qnear1←NEAREST(Qrand1,Ta);
9) Qnew1←NEW(Qnear1,Qrand1);
10) If NO COLLISION(Qnear1,Qnew1);
11) Ta.add(Qnew1),Ta.add(Qnear1,Qnew1);
12) Qnear2←NEAREST(Qrand2,Tb);
13) If NO COLLISION(Qnear2,Qnew2);
14) RETURN T(Ta,Tb);
15) SWAP(Ta,Tb);
16) Return Failure
算法步骤可总结如下:
1) 同时以起始点Qstart和目标点Qgoal为根节点生成随机树;
2) 利用目标偏向策略处理随机节点,ADJUST-STATE函数具体步骤:计算Qrand与Qgoal之间距离L以及Qrand指向Qgoal的方向向量β,则Qrand沿β进行扩展;
3) 经函数处理过的节点,得到Qnew,判断Qnear与Qnew连线之间是否有障碍,若是无则加入到随机树,若是有则返回重新处理;
4) 当两颗随机树最新节点距离小于一定阈值则Ta与Tb连接起来,否则继续进行扩展规划。
4. 实验与分析
为了验证STB-RRT算法及改进算法的性能,本文进行了仿真实验。
仿真环境设置为简单环境和复杂环境,如图4所示。简单地图是指在一定空间下,障碍物较少的地图;复杂地图是指障碍物数量多且尺寸大小不一,障碍物之间间距不一。地图大小为500*500,起始点均为(20, 20),目标点均为(490, 490)。本次实验环境为Intel(R) Core(TM) i7-8700 CPU、3.19 G,内存为32 G的计算机,编程环境为Matlab R2016a。
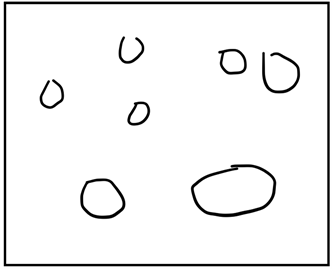 (a)
(a)  (b)
(b)
Figure 4. Experimental map. (a) Simple environment; (b) Complex environment
图4. 实验地图。(a) 简单环境;(b) 复杂环境
对比实验
为了验证本文算法的可行性,基于上述实验环境下,进行了两组实验:简单环境组(图5)和复杂环境组(图6)。每组分别运行传统BI-RRT算法、STB-RRT算法、修剪STB-RRT算法,实验进行50次,然后取均值进行比较。
 (a)
(a)  (b)
(b) 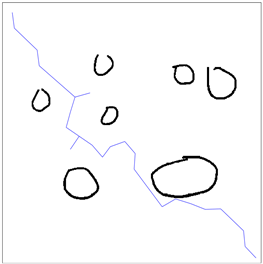 (c)
(c) 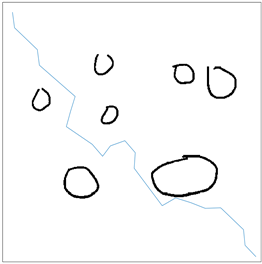 (d)
(d)
Figure 5. Planning diagram in a simple environment. (a) Conventional BI-RRT; (b) STB-RRT; (c) Trimming STB-RRT; (d) Improved path generation
图5. 简单环境下的规划图。(a) 传统BI-RRT;(b) STB-RRT;(c) 修剪STB-RRT;(d) 改进后生成路径

Table 1. Comparison of algorithm results
表1. 算法结果对比
由简单环境下的运行结果可得:基于目标偏向策略的STB-RRT算法与传统BI-RRT算法相比迭代次数减少35.29%,平均路径长度缩短11.54%,收敛速度提高19.95%。而加入修剪策略的STB-RRT算法通过对冗余节点的删除,实验结果显示:上述三项指标均得到提高。表1数据以及实验结果都证明了:在简单环境下该改进方法具有更高效率。
 (a)
(a)  (b)
(b) 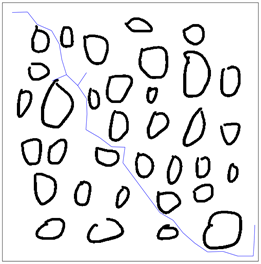 (c)
(c) 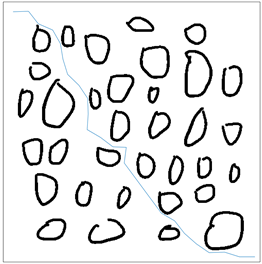 (d)
(d)
Figure 6. Planning diagram in complex environment. (a) Conventional BI-RRT; (b) STB-RRT; (c) Trimming STB-RRT; (d) Improved path generation
图6. 复杂环境下的规划图。(a) 传统BI-RRT;(b) STB-RRT;(c) 修剪STB-RRT;(d) 改进后生成路径

Table 2. Comparison of algorithm results
表2. 算法结果对比
由复杂环境下的运行结果可得,从时间性能上分析:STB-RRT算法比传统BI-RRT算法提高37.73%,加入修剪策略后算法提高55.44%;平均路径长度上分析:STB-RRT算法比传统BI-RRT算法缩短14.96%,加入修剪策略后算法缩短21.10%;迭代次数上分析:STB-RRT算法比传统BI-RRT算法减少40.00%,加入修剪策略后算法减少62.67%。以上三项指标性能均有明显提升,证实了:在复杂环境下,该改进算法具有较高效率。
由以上实验结果可以看出,本文所提出的改进策略,无论是环境的复杂度高与低,都具有同样的趋势。由于目标偏向以及修剪策略都从根本上减少了节点数量,所以实验结果中的迭代次数、收敛时间以及规划长度都有减少,最终达到优化算法,提高效率的目的。
上述实验图以及表1,表2综合来看,加入修剪策略算法相比STB-RRT算法时间长度,路径长度以及迭代次数上都有所提高。通过实验以及数据分析,可知本文中提出的STB-RRT算法真实有效,而加入删除冗余点策略的修剪STB-RRT算法相比原算法性能提升明显。
5. 结论
STB-RRT算法相比传统BI-RRT算法,加入了目标偏向策略,使随机树的生长更具有方向性,加快了两颗随机树的连通时间。考虑到扩展树生长中冗余现象的发生,在STB-RRT算法基础上,引入修剪策略,形成修剪STB-RRT算法。为了验证该改进策略的有效性,分别在不同代表环境下进行对比实验:简单和复杂环境下,传统BI-RRT算法、STB-RRT算法以及修剪STB-RRT算法分别实验,测量运行时间、路径长度、迭代次数数据并进行比较计算分析。经实验验证,该算法可以有效缩短算法运行时间、路径长度、迭代次数。通过在两种代表环境下进行实验,有效地证明了本文提出的改进算法可以通过目标导向以及删除冗余节点的原理提升算法规划效率,具有一定的普适性。在后续的研究中,将考虑在路径长度以及路径轨迹优化上进行展开。
基金项目
高校科研项目:基于桥梁病害检测无人机的航线规划研究(ky202107);
高校科研项目:面向人流分析的复杂背景地铁站行人检测技术研究(ky202015);
高校科研项目:无人机航拍车辆目标检测技术研究(ky202108)。
参考文献