基于可见图方法的股票行业分析

Stock Industry Analysis Based on Visibility Graph

摘要: 复杂网络已被广泛应用于探究复杂系统的规律。本文使用可见图方法，分别将道琼斯工业指数30支成分股的日收盘价序列映射到复杂网络，对股票可见图的性质进行了分析，探究股票市场的网络结构的变化。结果表明，首先，股票原始序列可见图的度分布表现为幂律度分布，而随机打乱之后的序列可见图度分布呈指数分布；其次，可见图的网络属性可以反应出股票序列的波动情况。最后，网络属性的聚类分析可以识别行业领域相近的股票序列。可见图方法从宏观的角度揭示不同地区股票市场的性质和潜在动力学行为，能有效解析股票市场对外界信息的反映效率，反映了股票市场是以非线性的方式对外界信息做出反应。

Abstract: Complex networks have been widely used to explore the laws of complex systems. This paper uses the visibility graph method to map the daily closing price series of 30 constituents of the Dow Jones Industrial Index to a complex network, to analyzes the characters of stocks’ visibility graphs, and explores the changes in the network structure of the stock markets. The results show that, firstly, the degree distribution of the visibility map of the original sequence of stocks is a power-law degree distribution, while the visibility degree distribution of the sequence after random disruption is ex-ponentially distributed. Secondly, the network properties of the visibility graph can reflect the fluctuations of the stock series. Finally, cluster analysis of network attributes can identify similar stock series in industry fields. The visibility graph method reveals the nature and potential dynam-ic behavior of the stock market in different regions from a macro perspective, which can effectively analyze the efficiency of the stock market's response to external information, and reflects that the stock market responds to external information in a non-linear way.

1. 引言

股票价格的波动是金融市场关注的焦点。它吸引了投机者，认为这是一个进行套利的机会，又扰乱了投资者，认为这是一种需要管理的风险。金融市场价格的时间属性和数学描述是现代定量金融中考虑的关键因素，在此基础上提出了金融模型来确定衍生产品价格和投资组合，并管理风险。自从1900年法国数学家提出，金融资产可以被定义为随机游走 [1]。随机游走一直是金融理论中采用的主要模型，如Black-Scholes公式，一种最流行的期权定价方法 [2]。随着数据的积累，真实的市场数据为金融时间序列的属性检验提供了样本，统计分布检验中表明大多数资产价格波动不是正态分布。Ramirez等 [3] 建议从信息熵的方法来研究股票市场，认为市场有效性是随着时间的推移而变化的，并且有时间尺度效应。Walid等 [4] 使用修正的香农熵(MSE)方法对原油市场弱形式效率的时变程度进行分析，所得研究结果表明，WT1市场和欧洲布伦特两个石油市场的弱形式市场效率随时间推移而变化，WT1市场的效率低于欧洲布伦特原油市场的效率。Walid [5] 采用修正的香农熵对市场有效性进行研究，实证结果表明股票市场有效性随着时间的推移而变化，并且在不同的市场和不同的地理区域具有不同的变化特征。Calragnile等 [6] 通过测量高频时间序列数据的熵来研究金融市场的相对信息效率。Mantegna [7] 使用最小生成树法(Minimum Spanning Tree, MST)对美国标准普尔500指数进行聚类分析，发现了股票市场中的层次化排列。

近些年，复杂网络方法作为分析动态复杂系统的新工具获得快速发展和广泛应用。网络理论为我们提供了一个新的视角和一个理解复杂系统整体关系的有效的工具。复杂网络理论可能是揭示时间序列中嵌入的信息的有力工具。但是如何从时间序列中构建网络仍然是一个需要解决的基本问题。Eom等 [8] 对美国和韩国的股票市场进行了研究，证实了使用最小生成树法方法获得的两个股票市场之间的网络度分布遵循幂律分布。Li等人 [9] 基于上证180指数和深证100指数的数据，采用平面最大滤波图(Planar Maximally Filtered Graph, PMFG)方法对股票市场进行建模，发现最小生成树关联网络和平面最大过滤图关联网络的宗派和派系聚类分析能有效地挖掘股票之间的聚类结构信息。Luo等人 [10] 构造具有临界值的网络，即通过将自相关值分别小于临界值重分配为0和1得到相邻矩阵。Rho等人 [11] 考虑了所构建网络的度分布函数的特征。在一个特殊的临界值下，度的分布将倾向于服从幂律。

Lacasa等(2008) [12] 提出了第一种基于可见性概念的方法，即自然可见性图(Natural Visibility Graphs, NVG)。可见图方法继承了时间序列的几个结构特性，该方法将周期级数映射到正则图上，将随机级数映射到随机图上，将分形级数映射到无标度图上。特别地，对于周期级数，图具有一个正则结构，其中度分布呈现了一个与级数的周期相关的一些峰值。对于白噪声过程，得到的图是完全随机的，度分布是一个指数函数。对于分形时间序列，度分布是与级数的分形性有关的幂律。在Lacasa等人 [13] (2009)的研究中，作者使用可见图来量化时间序列中的长程相关和分形。Yang等人 [14] 利用可见图方法将时间序列转换为复杂网络，结果表明原始序列的度分布可以很好地拟合幂律。Mutua等人 [15] 将序列段映射到可见图，作为对应状态的描述，并将连续发生的状态连接起来转化为复杂网络，提出了一种新的从网络的角度研究时间序列的方法。

基于价格(收益率)序列分布的经典“熵”统计模型只能刻画系统的“短程关联”，而可见图方法适合分析时间序列全局状态关联关系，因此基于网络方法，构建的模型更能量化度量系统的无序性程度，解决目前对股票只能进行定性检验的局限性。另外，可见图方法是一种非线性时间序列分析方法，能够解析混沌时间序列所暗含的非线性动力学特征。股票市场通常是以非线性的方式对外界信息做出反应，可见图方法能有效解析股票市场对外界信息的反映效率。

2. 准备工作

2.1. 数据

道琼斯指数是世界上历史最为悠久的股票指数，它的全称为股票价格平均指数。本文选取2010年1月至2020年4月道琼斯工业指数(Dow Jones Industrial Average, DJIA)中30支成分股每日的收盘价作为研究变量，其中每支成分股的长度T均为2500。道琼斯指数30支成分股名单如表1所示。股票的每日价格可以从公共网站https://cn.investing.com免费下载。

Table 1. 30 constituents of the Dow Jones Index

表1. 道琼斯指数30支成分股

2.2. 可见图方法

可见性网络有一个与时间序列的自然排序相关联的几何准则。基于可见性的算法包含了图特征中时间序列的全局和局部拓扑特征，易于实现，计算速度快。该方法在时间序列和复杂网络理论之间建立了连接的桥梁。在可见图算法中，每个时间序列点被视为一个直方，其高度等于节点值。当直方的顶部可见其他直方的顶部时，对应的复杂网络节点连边。

假设一组序列 $X=\left\{x\left(t\right)|t\in \mathbb{N},x\left(t\right)\in ℝ\right\}$，分位图方法将X映射为复杂网络 $g=\left\{N,A\right\}\in G$，N为节点集合，A为连边集合。时间序列中每一个节点 $x\left(t\right)$ 对应网络节点 $n_i$。形式上，可见图的节点集 $\left\{n_i\right\}$ 按时间顺序编号。如果处于时间节点a和b之间的任意节点c，满足不等式：

$x\left(c\right)\le x\left(b\right)+\left(x\left(a\right)-x\left(b\right)\right)\cdot \frac{b-c}{b-a}$ (1)

则说明节点a和b是可见的。图1为可见图方法的示例。

2.3. 可见图方法

2.3.1. 平均度

平均度是指整个网络中各个节点的度，而一个节点度的定义是该节点有多少其它节点与之相关联，所以整个网络的平均度可以一定程度上表示一个网络各个节点直接关联程度 [16]。平均度 $\bar{d}$ 计算公式如下所示：

$\bar{d}=\frac{{\displaystyle \sum d_i}}{N}$ (2)

其中， $d_i$ 为节点 $n_i$ 的度，N表示节点个数。

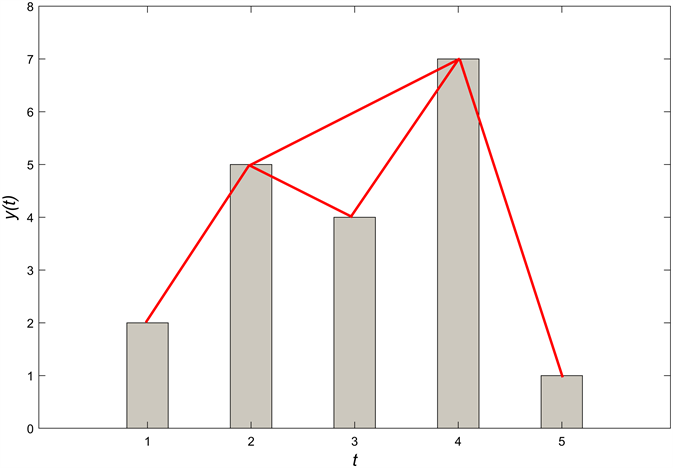
Figure 1. Convert time series into visibility graph

图1. 时间序列转化为可见图结构

2.3.2. 聚类系数

一些网络倾向于在相邻的顶点之间有更多的链接，因为它们的拓扑结构偏离了一个不相关的随机网络，其中三角形是稀疏的 [17]。这种模式被称为聚类，它反映了边缘分离到紧密连接的邻域。已有文献中通过各种尝试来研究加权网络的聚类系数。在这里，一个给定的节点 $n_i$ 的聚类系数由公式(2)给出 [16]：

$C{C}_i=\frac{1}{s_i\left(d_i-1\right)}\frac{{\displaystyle \underset{j,d}{\sum }\left(w_{ij}+w_{id}\right)}}{2}\left(a_{ij}{a}_{jd}{a}_{id}\right)$ (3)

其中 $w_{ij}$ 是加权矩阵 $W_k$ 中的一个元素，如果从节点 $n_i$ 到节点 $n_j$ 有连边，则为 $a_{ij}=1$，否则为0。 $d_i$ 为节点 $n_i$ 的总度数， $s_i$ 为节点 $n_i$ 的连边强度。整个网络的全局聚类系数，表示为CC，是由所有节点上的局部聚类系数的平均值来定义的。

2.3.3. 紧密中心性

紧密中心性(Closeness Centrality)用来衡量节点在其连通分量中到其它各点的最短距离的平均值 [18]。紧密中心性的取值范围是 $\left[0,1\right]$，数值越大越靠近中心。紧密中心性算法用于发现可通过图高效传播信息的节点，对于每个节点，紧密中心性算法在计算所有节点对之间的最短路径的基础上，还要计算它到其他各节点的距离之和，然后对得到的和求倒数，以确定该节点的紧密中心性。紧密中心性计算公式为：

$C\left(i\right)=\frac{n-1}{{\displaystyle \underset{v-1}{\overset{n-1}{\sum }}d\left(u,v\right)}}$ (4)

其中，u为待计算紧密中心性的节点，v为图中所有的节点数， $d\left(u,v\right)$ 是节点u和节点v之间的最短距离。

2.3.4. 同配系数

同配系数(Assortativity coefficient)是一种基于“度”的皮尔森相关系数，用来度量相连节点对的关系 [19]。如果总体上度大的节点倾向于连接度大的节点，那么就称网络的度正相关的，或者称网络是同配的；如果总体上度大的节点倾向于连接度小的节点，那么就称网络的度负相关的，或者称网络是异配的。通常来说，r的值在−1到+1之间，+1表示网络具有很好的同配模式，0表示网络是非同配的，−1表示这个网络负相关。标准的皮尔逊相关系数计算公式如下：

$r=\frac{{\displaystyle \underset{xy}{\sum }xy\left(e_{xy}-a_x{b}_y\right)}}{{\sigma }_a{\sigma }_b}$ (5)

其中， $a_x$ 和 $b_y$ 分别是在值为x和y的顶点上开始和结束的边的分数， ${\sigma }_a$ 和 ${\sigma }_b$ 是分布的 $a_x$ 和 $b_y$ 的标准差， $e_{xy}$ 是网络中所有边的比例，满足：

$\{\begin{array}{l}{\displaystyle \underset{xy}{\sum }{e}_{xy}=1}\\ {\displaystyle \underset{y}{\sum }{e}_{xy}=a_x}\\ {\displaystyle \underset{x}{\sum }{e}_{xy}=b_y}\end{array}$ (6)

为了计算具有指定顶点和边的实际网络的同配系数r，我们可以将其重写为下列形式：

$r=\frac{{\displaystyle \underset{i}{\sum }{j}_i{k}_i-M^{-1}}{\displaystyle \underset{i}{\sum }{j}_i{\displaystyle \underset{i^{\prime }}{\sum }{k}_{i^{\prime }}}}}{\sqrt{\left[{\displaystyle \underset{i}{\sum }{j}_i^2-}{M}^{-1}{\left({\displaystyle \underset{i}{\sum }{j}_i}\right)}^2\right]\left[{\displaystyle \underset{i}{\sum }{k}_i^2-}{M}^{-1}{\left({\displaystyle \underset{i}{\sum }{k}_i}\right)}^2\right]}}$ (7)

其中， $j_i$ 和 $k_i$ 表示节点i的入度和出度，M是边数。对于一个无向网络，我们可以简单地用两个无向边替换每个指向相反方向的有向边。

3. 结果

我们将可见图方法应用于道琼斯工业指数30支股指收盘价序列，以探究不同行业股指序列的动力学特征行为。

3.1. 长程相关性

根据L. Lacasa等人的 [13] 的研究，一个具有分形特征的时间序列可见图网络存在幂律分布。为了检验股票收盘价序列的自仿射特征，我们计算了30支行业股指的可见图网络度分布。图2(a)为苹果公司股票序列的度分布，它表现为幂律度分布。为了与此结果进行比较，我们还计算了失去其原始时间相关性的随机序列的度分布。图2(b)表明，随机打乱后的序列不是幂律分布，而是指数分布。此外，其他29支股票序列的度分布情况均符合幂律分布。这表明，股票价格序列是具有长程相关性的分形时间序列。

3.2. 网络属性

对于30支行业股指，我们用可见图方法将时间序列转化复杂网络，得到了邻接矩阵 $\left\{G\right\}$。对于 $g_k\in G,k=1,2,3,\cdots ,30$，分别计算平均度、聚类系数、紧密中心性和同配系数。计算结果如图3所示：

首先，网络的平均度可以一定程度上表示一个网络各个节点直接关联程度。如图3(a)所示，节点7代表的股票序列，即杜邦公司的股票序列，其可见图平均度较高，说明杜邦公司股票收益率的波动较其

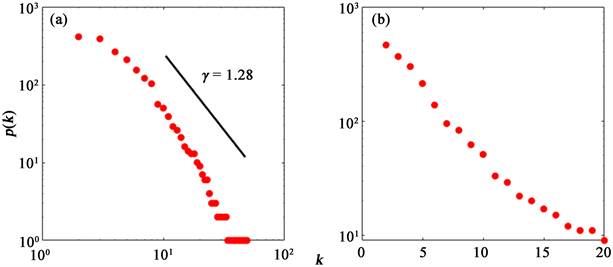
Figure 2. Degree distribution of original series and random series

图2. 原始序列和随机序列的度分布

Figure 3. The average degree, clustering coefficient, closeness centrality, and assortativity coefficient of stocks’ visibility graphs

图3. 股票序列可见图的平均度、聚类系数、紧密中心性、同配系数

他股票大。结合实际情况，杜邦公司股票在2019年至2021年间存在大幅涨跌。而节点10，高盛集团的股票序列对应可见图网络的平均度较小，说明其收益涨幅情况较为平稳。其次，聚集系数可以分析出网络的形状是否规则覆盖面以及集中性。图3(b)显示苹果公司股票序列可见图的聚类系数最大，表明苹果公司在全局范围内存在的大幅波动较少。除了2020年8月31号苹果公司进行拆股，导致股价异常波动外，其他时间涨跌相对平稳。图3(c)展示了30支股票序列可见图的紧密中心性，紧密中心性反映在网络中节点之间的紧密程度。紧密中心性表现最差的是辉瑞制药有限公司的股票序列。全球疫情下，辉瑞公司制药业务收入排名从2021年的第8名提升至2022年的第1名，其股票随之出现较大波动。最后，如图3(d)所示，30支股票可见图的同配系数均大于0，说明网络呈现同配性结构。其中，杜邦公司股票序列可见图的同配系数接近0，更加说明了该公司股票收益的波动较大。

3.3. 聚类分析

本文采用K-Means算法，将提取的4个网络属性作为特征，对30支股票序列进行聚类分析。K-Means算法采用迭代的方式进行聚类。结果显示可见图方法可以将行业相同的股票序列归为同类。例如类别1中包括电子、互联网、软件、娱乐等行业，类别2中主要是金融业等。聚类结果如表2和图4所示：

Table 2. 30 constituents of the Dow Jones Index

表2. 道琼斯指数30支成分股

Figure 4. Clustering results

图4. 聚类结果

4. 结论

复杂网络已被广泛应用于揭示复杂系统的规律。可见图方法是将时间序列转化为复杂网络的有效工具。本文从复杂网络的角度来考虑股票市场，通过可见图方法将道琼斯工业指数30个股票收盘价序列映射到转移网络，利用该方法对不同行业股票的特性进行了分析，分析股票序列全局状态关联关系。

结果表明，可见图方法可以保留股票序列的全局信息，判断序列的长程关联关系，并且在一定程度上反映股票序列的阶段波动率情况。首先，股票原始序列可见图的度分布表现为幂律度分布，而随机打乱之后的序列可见图度分布呈幂律分布；其次，可见图的网络属性可以反映出股票序列的波动情况。最后，把网络属性作为特征，采用聚类方法对股票序列进行分类，可以将行业领域相近的股票序列归为一类。

可见图方法可以量化与信号的潜在动力学相关的长程相关性或反相关性等特征，以一种新的、有效的方式扩展了传统的时间序列分析工具，揭示了股票序列可见图网络的特征，为其背后的价格波动机制指明了研究方向。

基金项目

国家自然科学基金(批准号：12275179)资助的课题。

参考文献

NOTES

^*通讯作者。