新建5G基站的站址规划研究——基于优化算法及动态规划模型

Research on Site Planning of New 5G Base Station—Based on Optimization Algorithm and Dynamic Programming Model

摘要: 针对新一代5G通信基站的建设及其站址规划问题，本文提出了一种基于粒子群优化算法与模拟退火算法的动态规划模型的站址规划方法。该模型考虑了基站覆盖半径、基站类型以及信号覆盖范围等因素，并利用广东湛江地区原有的基站业务数据来进行建模。实验结果表明，本文提出的粒子群优化算法与模拟退火算法可以有效地对地区的基站选址进行规划，并对实际的基站建设提供一定程度的参考。

Abstract: Aiming at the construction and site planning of the new generation of 5G communication base sta-tions, this paper proposes a site planning method based on the dynamic programming model of particle swarm optimization algorithm and simulated annealing algorithm. The model CONSIDERS THE base station coverage radius, base station type, signal coverage range and other factors, and uses the original base station service data in Zhanjiang, Guangdong Province to model. The experi-mental results show that the proposed particle swarm optimization algorithm and simulated an-nealing algorithm can effectively plan the location of the base station in the ground-to-ground area, and provide a certain degree of reference for the actual base station construction.

1. 引言

5G是第五代通信技术，具有高传输效率、低延迟性和链接数大的特点。2018年12月10日工信部正式对各运营商发放牌照，标志着5G商用测试的开始，随着通讯技术的快速发展，5G网络的建设也随之到来。随着5G的发展，基站的网络规划也变得格外重要。5G基站是5G网络的核心设备，其存在的重要价值就是提供无线覆盖服务，确保有线通信网络和无线终端的无线信号传输。可以说基站的架构以及形态会对5G网络的部署带来直接而又深刻的影响，所以优秀的选址可以提高基站网络的覆盖效益，减少基站的修建数量从而减少施工成本。然而适合基站布局的站址变得越来越稀少。同时在整个通信网络规划中，合理的基站选址方案是至关重要的一部分。合理的基站布局能够节省大量的空间资源，使成本、布局规划等多方面都得到巨大的改善。在2G乃至4G的时代中，大部分选址方法都是人工手动设计规划来确定各基站间的地址以及位置关系，而5G基站基数规模大，覆盖范围也有大有小，显然人工方法不足以得到最优的结果 [1]。

基于广东湛江区域现有的基站数据，本文考虑构建一个动态规划模型来求出新建基站的最优建址。同时此基础上尽可能的优化基站覆盖范围 [2]。具体来说本文的贡献如下：

首先将现有基站数据区域用很小的栅格进行划分，只考虑到每个栅格的中心点，经过划分该区域大小为2500 * 2500个栅格，可得到该区域中182,808个业务点的坐标及其业务量和1475个已建基站的坐标。接着对站址进行选择，明确目标函数(即建造基站总成本最低)及其约束条件，并根据现有业务点的坐标和现有基站的坐标计算得到二者之间的距离矩阵，在此基础上分析得到业务量的大致分布情况。下一步将构建模糊聚类模型对业务点坐标进行聚类分类，得到选定区域内聚类后的类中心坐标。最后以聚类所得的各个类中心坐标为基站坐标进行规划，使得业务点总业务量的90%被规划基站覆盖，使用粒子群算法与模拟退火算法进行求解该动态规划模型，通过对比两种算法所求出的最小成本，并判断其优劣性以得到新建基站的最优建址。

2. 基于粒子群优化与模拟退火算法的动态规划模型

2.1. 对于原始基站坐标的模糊聚类

模糊聚类 [3] 是一种应用模糊数学方法，通过计算样本属于各个类别的不确定性程度，进行聚类分析。通过使用SPSS对广东湛江地区的通信业务点坐标数据进行模糊聚类，在参数设置中将聚类个数设置为2000，迭代次数为10，结果如表1所示。

Table 1. Fuzzy clustering results

表1. 模糊聚类结果

2.2. 构建0~1背包问题的动态规划模型

背包问题(Knapsack problem)是一种组合优化的NP完全问题。其可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，该如何选择才能使得物品的总价格最高。

为了探究多种限制条件下的基站最优建址，本文考虑构建一个基于解决0~1背包问题的动态规划模型 [4]。假设需要选择n个基站(基站总价格为成本，即背包容量W)，基站i的服务量为 $v_i$，成本为 $w_i$，且基站的服务量和服务成本都是非负的。

为了使得业务点总业务量的90%被规划基站覆盖。本文对确定的基站点选择宏基站还是微基站进行规划，引入0-1变量： $p_i$， $q_i$。

使其满足：

$p_i,q_i=\{\begin{array}{l}0,不选该基站\\ 1,选择该基站\end{array}$ (1)

令 $V\left(i,j\right)$ 为前i个基站中能够选择服务量为j的最大的基站服务量，把前i个物品装入容量为0的背包和把0个物品装入容量为j的背包，价值均为0。

$V\left(i,0\right)=V\left(0,j\right)=0$ (2)

如果第i个基站的服务量小于或等于总服务量 $j\ge w_i$，即还有足够的容量，但装入了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，则可得动态规划函数为：

$V\left(i,j\right)=\max \left\{V\left(i-1,j\right),V\left(i-1,j-w_i\right)+v_i\right\},j\ge w_i$ (3)

如果第i个基站的服务量大于总服务量 $j<w_i$，则选择前i个基站得到的最大服务量和选择前 $i-1$ 个基站得到的最大服务量相同，即基站i不选择。

$V\left(i,j\right)=V\left(i-1,j\right),j<w_i$ (4)

1) 如果选择第i个基站，则基站总服务量等于把前 $i-1$ 个基站装入容量为 $j<w_i$ 的背包中的价值加上第i个基站的服务量 $v_i$ ；

2) 如果第i个基站没有选择，则新建基站中的服务量等于前 $i-1$ 个基站装入容量为j的背包中所取得的价值。取二者中价值较大者。接着对考虑每一次迭代情况：

step 1：只选择前1个基站，确定各种情况下的总服务量能够得到的最大价值；

step 2：只选择前2个基站，确定各种情况下的总服务量能够得到的最大价值；

……

step n：只选择前n个基站，确定各种情况下的总服务量能够得到的最大价值；

最后， $V\left(n,W\right)$ 便是容量为W的背包中装入n个物品时取得的最大价值。

为了得到 $V\left(n,W\right)$，需向前推到 $V\left(n-1,W\right)$。如果 $V\left(n,W\right)>V\left(n-1,W\right)$，则第n个基站装入背包，前 $n-1$ 个基站装入容量为 $W-w_i$ 的背包中；否则，第n个基站没有被装入背包，前 $n-1$ 个基站被装入容量为W的背包中。

直到确定第一个基站是否被选择。在此基础上，建立业务量最大的0-1整数规划模型，模型中的决策变量以及目标函数、约束条件如下：

决策变量：新建基站的坐标；

目标函数：新建基站所需要的最少成本；

约束条件：

· 业务点与新基站之间的距离至少应小于30；

· 每一个业务点只能选择一个宏基站或微基站；

· 两个新建基站之间的门限不能小于10。

综上所述得到基本的动态规划模型如下：

$\begin{array}{l}\max W={\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_j{p}_i}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_j{q}_i}\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}{\displaystyle \underset{i=1,j=1}{\overset{n}{\sum }}{w}_j{p}_i}+{\displaystyle \underset{i=1,j=1}{\overset{n}{\sum }}{w}_j{q}_i}\ge 6350607\\ p_i=0,1\\ q_i=0,1\\ \sqrt{{\left(x-x_0\right)}^2-{\left(y-y_0\right)}^2}\le 30,\left(x,y属于宏基站\right)\\ \sqrt{{\left(x-x_0\right)}^2-{\left(y-y_0\right)}^2}\le 10,\left(x,y属于微基站\right)\end{array}\end{array}$ (5)

2.3. 变量参数设置

2.3.1. 粒子群算法变量参数设置

粒子群算法，也称粒子群优化算法或鸟群觅食算法(以下缩写为PSO)，是一种新的进化算法。PSO算法属于进化算法中的一种，和模拟退火算法相似，它也是从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质，但是比遗传算法规则更为简单，并没有遗传算法的“交叉”和“变异”操作，它通过追随当前搜索到的最优质来寻找全局最优。这种算法以其容易实现、精度高、收敛快等优点引起重视，并在解决实际问题中展示了其优越性。粒子群算法是一种并行算法，也是一种进化计算技术。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解。粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置，相对于其他智能算法来说更加快速 [5]。

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示当前维度的一个向量：

$X_i=\left(x_{i1},x_{i2},\cdots ,x_{iD}\right),i=1,2,\cdots ,N$ (6)

并且它此时的飞行速度也表示为一个向量：

$V_i=\left(v_{i1},v_{i2},\cdots ,v_{iD}\right),i=1,2,\cdots ,N$ (7)

将这个粒子搜索到的最佳位置记为个体极值，即：

$P_{best}=\left(p_{i1},p_{i2},\cdots ,p_{iD}\right),i=1,2,\cdots ,N$ (8)

直到将整个粒子群所搜索到的最优位置记为全局极值，即：

$g_{best}=\left(g_1,g_2,\cdots ,g_D\right)$ (9)

找到这两个最优值后，粒子将根据以下公式来更新自己的位置和速度：

$v_{ij}\left(t+1\right)=v_{ij}\left(t\right)+c_1{r}_1\left(t\right)\left[p_{ij}\left(t\right)-x_{ij}\left(t\right)\right]+c_2{r}_2\left(t\right)\left[p_{gj}\left(t\right)-x_{ij}\left(t\right)\right]$ (10)

其中粒子的标号为 $i=1,2,\cdots ,m$ ；k为迭代代数； $c_1$ 和 $c_2$ 称为学习因子1和学习因子2， $r_1$ 和 $r_2$ 则是范围[0, 1]内的随机数，以此来增加粒子起飞时的随机性。为了控制 ${\stackrel{\to }{V}}_i^k$ 和 ${\stackrel{\to }{X}}_i^k$ 的值在合理的区域内，需要指定 $V_{\max }$ 和 $V_{\min }$ 来限制，在参考相关文献 [6] [7] 的基础上，本文加上了惯性权重，这样在模型搜索最优解时可以动态调整惯性权重，保证在算法开始时各粒子可以在较大的速度步长内进行全局搜索，目前采用较多的是线性递减权值策略，表达式如下：

$v_{ij}\left(t+1\right)=v_{ij}\left(t\right)+c_1{r}_1\left(t\right)\left[p_{ij}\left(t\right)-x_{ij}\left(t\right)\right]+c_2{r}_2\left(t\right)\left[p_{gj}\left(t\right)-x_{ij}\left(t\right)\right]$ (11)

参数的选择通常会影响算法的效率以及性能，如何选择参数是一个复杂的优化问题，通常由实验者反复调试来决定。本文导入以上求得的聚类中心坐标，先不断地调整关键参数，观察收敛趋势以及收敛速度，发现当惯性权值处于0.8~1.0之间时粒子群算法具有较高的收敛速度，对规划模型的求解准确度也会相应的增加。在反复调试后令其等于0.85，此时收敛速度较快且规划问题求解处于一个最优的水平。本文最终次所使用的粒子群算法主要参数如表2。

Table 2. Main parameter list

表2. 主要参数表

粒子群算法的求解流程图如图1所示。

2.3.2. 模拟退火算法变量参数设置

模拟退火算法是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。

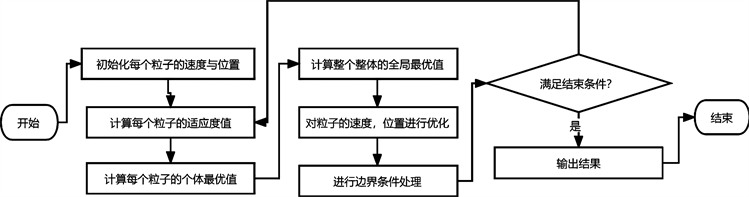
Figure 1. Particle swarm optimization solution flow chart

图1. 粒子群算法的求解流程图

模拟退火算法有两层循环。循环一：反复迭代产生新解，在降温的过程中的任一温度下通过随机扰动产生新解，并计算目标函数值的变化，决定是否被接受。循环二：缓慢降温重复迭代过程，在固定温度下迭代完成后缓慢的降低温度，让算法最终可能收敛到全局最优解。

由于算法初始温度比较高，通过循环一的反复迭代过程，让使目标函数值增大的新解在初始时也可能被以一定的概率接受，因而能跳出局部极小值。并且，虽然在低温时接收函数已经非常小了，但仍不排除有接受更差的解的可能，因此本文把退火过程中碰到的最好的可行解(历史最优解)也记录了下来，并让它与终止算法前的最后一个被接受解一并输出，防止遗漏最优解。

而在退火的过程由一组初始参数，即冷却进度表(cooling schedule)控制，它的核心是尽量使系统达到准平衡，使算法在有限的时间内逼近最优解。

模拟退火算法主要有以下部分组成 [8]。

1) 控制参数T_i的选择及初值

选择T_i为控制参数，每个控制参数T_i对应的解为X_i。根据对全局最优解和搜索范围的初步分析，结合问题的规模，本文选择初值T₀为0.5。

2) 控制参数R_i的衰减函数

通过构造衰减函数来对程序进行“降温”处理

$\{\begin{array}{l}{T}_{i+1}=T_i-1,\left(T_i\ge 1\right)\\ T_{i+1}=T_i-0.1,\left(T_i<1\right)\end{array}$ (12)

常用的衰减函数为 $T_{i+1}=\alpha T_i,i=0,1,2,\cdots$。其中 $\alpha$ 可以取值为0.5~0.99。

3) Markov链长度

已知Markov链长度的选取应满足在控制参数的每一个取值上达到准平衡状态，对简单的情况可直接令 $L_i=100n$，n为问题规模， $L_i=500$。

4) 接受函数

$p\left(i\Rightarrow j\right)=\{\begin{array}{l}1,当f\left(i\right)\le f\left(j\right)\\ \exp \left(\frac{f\left(i\right)-f\left(j\right)}{k{L}_i}\right),其他\end{array}$ (13)

当 $L_i$ 比较大的高温情况下，指数上的分母比较大，且此时这是一个负指数，所以接受的概率接近于一。即比当前解 $x_i$ 更差的新解 $x_j$ 也可能被接受，因此便提供了跳出局部最优解的可能。

5) 停止条件

$L_i=L_f=0.01$ (14)

在高温时已经进行了充分的广域搜索，找到了可能存在最好解的区域，而在低温在进行足够的局部搜索，则就很有可能找到全局最优解了，因此对 $L_f$ 设置了一个足够小的数 [9]。最后确定冷却进度表的各项参数如表3所示。

Table 3. Automation professional practice teaching system diagram

表3. 自动化专业实践教学体系图

3. 仿真实验

实验结果

通过前文对两种算法分别构建好的规划模型进行优化迭代计算，最终求得两种优化算法解出的最小成本，模拟退火算法和粒子群算法的仿真结果分别如图2和图3所示。通过对两种算法的迭代结果的对比分析，可以发现对于规划模型而言，模拟退火算法收敛速度较慢，并且随着迭代次数的增加结果仍然存在不稳定性。而粒子群算法收敛速度较快并在较少的迭代次数时结果就已经具有了稳定性，并且结果相较于图二更优。综上本文采取了粒子群优化算法求解的结果作为最终实验结果。

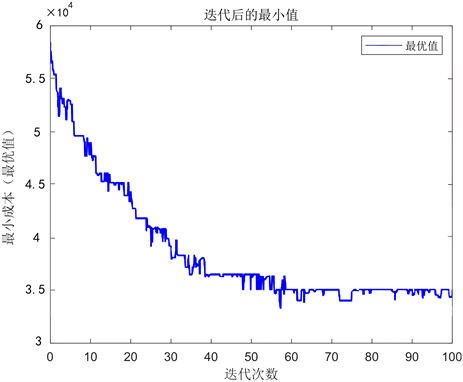
Figure 2. Results of simulated annealing

图2. 模拟退火算法结果

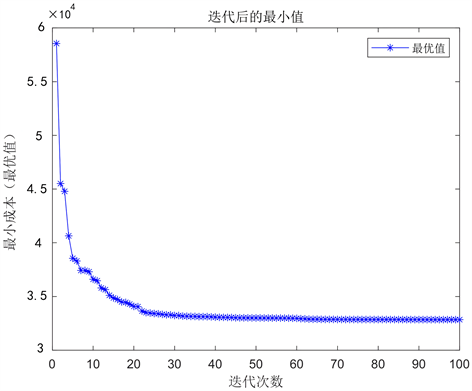
Figure 3. Results of particle swarm optimization

图3. 粒子群算法结果

由图3结果可知，本文提出的算法收敛速度极快，具有粒子群算法的最大优点，该算法所具有的飞跃性特性能够极快的找到全局最优解并且不会被困在局部最优，避免了其他类似优化算法的求解速度慢、求解困难等缺陷，因此在5G基站的站址规划研究上具有较好的参考运用价值。最后将实验结果中对每个站址宏微基站的选择结果与数据进行匹配，并对这些基站的分布进行可视化分析，如图4和图5所示。

通过粒子群算法得出的结果及其可视化分析可以得出需要建设的宏基站个数为3303个，在此地区的分布较为均匀。需要建设的微基站个数为217个，主要分布在区域的右下角。在此时新建基站的业务量占弱覆盖点总业务量的90.532%，同时总成本达到最小值33,247。

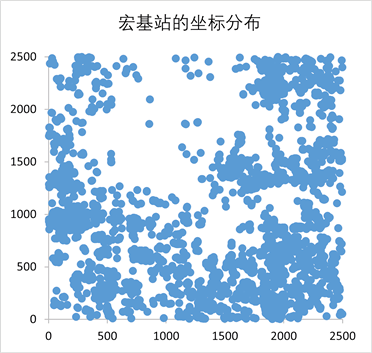
Figure 4. Coordinate distribution of Acer station

图4. 宏基站的坐标分布

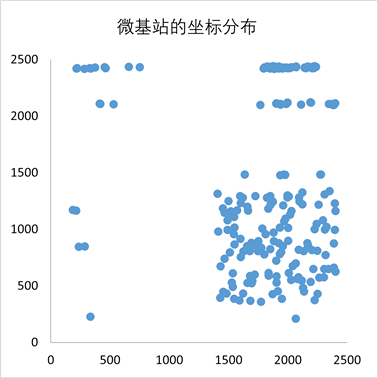
Figure 5. Coordinate distribution of microbase station

图5. 微基站的坐标分布

4. 结论

本文讨论分析了基于广东湛江地区现有基站及业务数据的5G基站建址规划成本的数学模型，并结合粒子群以及模拟退火算法探究优化问题的解决方案。由于各个方面的限制及考虑，本模型仅结合参考了基站覆盖半径、基站类型以及信号覆盖范围这几个因素。后续研究中可以考虑每个基站的网络容量，更多基站类型，基站实际覆盖角度范围等因素 [10] [11]，使得模型能够在实际的站址规划中起到更高的参考价值。

基金项目

获得了广东省2022年攀登计划项目支持，项目编号为pdjh2022a0231。

NOTES

^*通讯作者。