揭示微积分的基本思想方法——用以指导微积分的教学

Revealing the Basic Idea and Method of Calculus—To Guide the Teaching of Calculus

摘要: 遵循“用‘已知’认识‘未知’、用‘已知’研究‘未知’、用‘已知’解决‘未知’”这一基本认知准则，通过分析变速直线运动的瞬时速度(引出导数)和变速直线运动的路程(引出定积分)问题，揭示微积分的基本思想方法。与导数、定积分、重积分、曲线积分及曲面积分等相关的问题的解决都遵循微积分的基本思想方法。这一思想方法的揭示统一了微分学与积分学的基本思想方法，对减轻微积分教学难度，提高教学质量，使学生学到微积分的真谛产生积极影响。

Abstract: “Using known knowledge to learn unknown facts, to explore unknown world, and to solve un-known problems” is a basic cognitive principle. We follow this principle to analyze the instanta-neous speed and the distance of variable rectilinear motion, which extract the concepts of derivative and integral respectively, and then to reveal the basic idea and method of calculus. From the analysis of the practical examples, we can see that the resolving of the problems related to derivative, definite integral, double integral, triple integral, curvilinear integrals and surface integral all follow the basic idea and method of calculus. The basic ideas and methods of differential calculus and integral calculus are unified. The study of this methodology can reduce the calculus teaching difficulty, improve the teaching quality and bring students a thorough understanding of core knowledge behind calculus.

1. 引言

用“已知”认识“未知”、用“已知”研究“未知”、用“已知”解决“未知”是人类认识世界的基本认知准则；也是人类文明发展的基本规律，人类文明的每一步前进、科学技术的每一个发现与发明无不遵循这一规则 [1]。我们所学习的知识是前人智慧的结晶，但不是历史的重现，而是后人依据这一认知准则整理总结前人的成果得到的。学生学习它也理应依照这一准则来接受、传承。

被认为是20世纪举世无双的数学教育家、数学方法论大师波利亚在评价伟大的瑞士数学家欧拉时说：“在前辈数学家中欧拉对我影响最大。主要原因在于，欧拉做了一些跟他才能相当的伟大数学家从未做过的事，即他解释了自己是如何发现其研究结论的。对此，我如获至宝”。欧拉之所以在育人方面获得高度赞誉，培养出许多杰出的数学家，波利亚给出了回答：他不仅使学生知道“是什么”，“怎样做”更使学生知道“为什么”、“怎么想”。“是什么”、“怎样做”是告诉知识和技能；“为什么”、“怎么想”是在传授思想，使学生学到学科的灵魂。学生知道了“为什么”、“怎样想”，学会“悟”与“思”，才能发现问题、提出问题、解决问题，实现创新。

这就是说，教师对学生不能授之以鱼而要受之于渔，不能只讲授僵死的知识，更要使学生学到知识中的思想与方法。只有学到知识蕴含的思想，才能学到知识的精髓与真谛，才能变知识为智慧。

2. 微积分思想方法的发展

数学的发展大体经历了三个阶段，一是大约从古希腊时代至十七世纪中叶，由于当时生产力水平落后，社会发展缓慢，人们的认知水平受到很大的限制，看到客观世界中的各种事物都是孤立的、静止不变的，研究所涉及的量只是常量，图形也只是诸如直线、平面所围成的“规则”的几何图形。这一时期的数学称之为“初等数学”，也称为常量数学。中学阶段所学习的数学大都属于这个阶段的内容。二是大约从1637年至19世纪末。这个阶段随着欧洲工业革命的发展，生产力得到极大的提高，实现了从工厂手工业向机器大工业过渡，机器的发明和应用成为这个时代的标志。人们认识到事物是运动的，看到也是复杂的、不规则图形，仅靠初等数学已远不能满足实际需求，对数学提出了新的挑战，急需建立新的数学工具。比如，计算沿直线做变速运动的质点在某一时刻的瞬时速度及某段时间内所走过的路程；再比如计算变力做功、曲线的切线、曲边形的面积、函数的最值、曲线的长度等等，研究这些问题就要研究变量。在这类问题的刺激下，数学得到了快速发展。特别是1637年笛卡尔发明了直角坐标系，创立解析几何，牛顿、莱布尼兹创建了微积分，为研究变量建立了一套新的运算规则，有效地解决了上面所提出的典型问题。这个时期的数学称为“高等数学”或为“变量数学”。第三阶段就是从19世纪末至现在，这一“现代数学”阶段。

在“变量数学”时期，绝大多数科学家都致力于研究速率、切线、极值、面积问题，尤其是刻画运动与变化的无限小算法，这一时期的数学得到迅猛发展，取得了许多突破性的成果，如天文学家开普勒利用无穷小求和的思想求得曲边形的面积及旋转体的体积，法国数学家费马找到具体方法来求曲线的切线及函数的极值，特别是解析几何的创立对微积分的建立起到了极大的推动作用。受笛卡尔《几何学》和沃利斯的《无穷算术》的影响，牛顿在1665~1666年间，发明了正流数术(微分)和反流数术(积分)，标志着微积分的诞生。同一时期，德国数学家莱布尼茨于1684年发表了第一篇微分论文，定义了微分的概念并引入其符号；1686年发表了积分论文，引入积分符号，讨论了微分与积分的关系。牛顿和莱布尼兹分别从物理学和几何学的角度出发各自独立地开创了微积分，但起初其理论分析基础是混乱和模糊不清的。之后，法国数学家柯西严格化地建立了微积分理论的核心基础——极限，并定义了函数的连续性、将导数看成差商的极限、将定积分看成和的极限、给出微积分基本定理的现代形式和证明等。柯西对微积分学的贡献是巨大的，其极限理论的创立使得微积分从此建立在严密的分析基础之上。20世纪最杰出的数学家之一冯·诺依曼在评价《微积分》时写道：“《微积分》是现代数学取得的最高成就，而且对它的重要性怎样评价都不为过。”

从文献 [2] [3] [4]，不难看出微积分作为数学学科里逻辑思维最为清晰、客观性最强的一个分支，其具有至关重要的地位。而要将将微积分的思想融入到高等数学的学习中，甚至应用到实际问题中，确实非常困难的。微积分之所以被公认为难，是理工科大学生谈虎色变的课程，没有使学生明确学习微积分所要遵循的基本思想是其重要原因。从中小学学习的常量数学到微积分这一变量数学是一大跨越。虽然这是一大跨越，但是，认识、研究这一“未知”也必然要遵循用“已知”认识“未知”、研究“未知”，解决“未知”这一人类的基本认知准则。这里的“已知”是指我们已有的知识、方法、技能等，不论它是来源于书本还是来源于生活实践；所谓“未知”是指要学习、要研究、要解决的问题。这一认知准则同时也是人类文明发展所遵循的基本规律。人类文明的每一步前进，科学技术中的每一个发现，无不遵循这一规则。无疑，教材中所给出的知识，其形成也必然遵循这一规则，学生接受它也必须按照此规则。学生接受起来之所以困难，主要是通常教材的编写及授课者未能按照此规则传授给学生，未能用微积分的基本思想来揭示微积分的基本概念，给微积分蒙上了一层厚厚的面纱，掩盖住了微积分研究问题的方法的本质，使学生不能清晰地认识到学习微积分这一“未知”，需要用研究、解决常量数学中相关问题的方法作“已知”，茫茫然、不知所以然。这是造成学生接受、应用微积分困难的重要原因。

因此，教师教授微积分，应利用“用‘已知’认识‘未知’、用‘已知’研究‘未知’、用‘已知’解决‘未知’”这一基本认知准则层层剖析，将要学习的“未知”一步步转化为“已知”。下面利用这一认知规则，揭示微积分的基本思想方法。

3. 揭示微积分基本思想方法

3.1. 瞬时速度问题揭示微分学基本思想

为引入导数的概念，首先讨论下述瞬时速度问题。

设一质点沿直线做变速运动，它所走过的路程与时间的关系为 $s=s\left(t\right)$。求质点在 $t_0$ 时刻的速度 $v\left(t_0\right)$ (称为 $t_0$ 时刻的瞬时速度)。

何谓变速运动的瞬时速度？怎样计算？这些都是“未知”。为研究这一“未知”，我们自然想到熟知的“匀速运动的速度”这一“已知”。下面就用求匀速直线运动的速度公式作“已知”来研究变速直线运动的瞬时速度及其计算。

由于匀速运动的速度等于路程除以所用的时间，为此在 $t_0$ 附近另取一时刻 $t_0+\Delta t$ ( $\Delta t\ne 0$ )，质点从 $t_0$ 到 $t_0+\Delta t$ 时刻所走过的路程为 $s\left(t_0+\Delta t\right)-s\left(t_0\right)$，所用时间为 $\Delta t$。我们将这段时间内的非匀速运动近似看作匀速运动(“以‘匀’代‘非匀’”，图1)，利用匀速运动的速度计算公式，得

$\bar{v}\left(t\right)=\frac{s\left(t_0+\Delta t\right)-s\left(t_0\right)}{\Delta t}$。

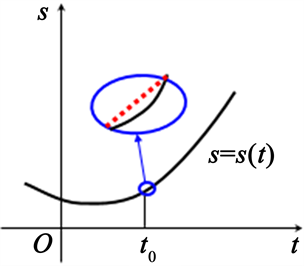
Figure 1. Diagram of replacing non-uniform with uniform

图1. 以“匀”代“非匀”示意图

对变速运动来说， $\bar{v}\left(t\right)$ 实际就是 $t_0$ 到 $t_0+\Delta t$ 这段时间内的平均速度，它可以看作 $t_0$ 时刻的速度 $v\left(t_0\right)$ 的近似值，即

$v\left(t_0\right)\approx \frac{s\left(t_0+\Delta t\right)-s\left(t_0\right)}{\Delta t}$。

显然， $\left|\Delta t\right|$ 越小近似程度越高。对 $\bar{v}\left(t\right)$ 关于 $\Delta t\to 0$ 取极限，若该极限存在，就把此极限值称作 $t_0$ 时刻的瞬时速度 $v\left(t_0\right)$，即

$v\left(t_0\right)=\underset{\Delta t\to 0}{\lim }\frac{s\left(t_0+\Delta t\right)-s\left(t_0\right)}{\Delta t}$。

上面研究的变速运动是非均匀变化问题。对此我们遵循“用‘已知’研究‘未知’”的认知规律，局部采取“以匀代非匀”——在局部小范围内近似看作均匀变化(匀速运动)——将问题转化为初等问题，从而用初等方法求出其近似值(平均速度)，再通过求极限得到其精确值。这正是微积分研究问题的基本思想方法。将上述研究的问题抽象为一般，就得到导数的概念。

所谓导数，实际是研究均匀变化量的变化率所用的“除法”在研究非均匀变化量的变化率中的延伸。也就是用均匀变化量的变化率这个“已知”来研究非均匀变化量的变化率。

通过研究变速运动的瞬时速度总结出的微积分的基本思想方法，是研究非均匀变化(分布)的量所普遍遵循的规律，后面在研究非均匀变化(分布)的量时，直接利用这一思想方法，不论是教师讲授、还是学生接受都会非常轻松。降低学习微积分的难度。

3.2. 变速运动路程问题揭示积分学基本思想

定积分研究的对象同样是非均匀变化的量，只不过导数是“微观”地研究该变量在某一点处的变化率，而定积分是“宏观”地研究非均匀变化量在某区间上的整体值。虽然它们之间有着“微观”与“宏观”的差异，但既然研究的对象都是非均匀变化的量，因此所遵循的思想方法是一致的，都要局部“以匀代非匀”，将非均匀变化的“未知”转化为均匀变化的“已知”，从而用初等方法求出其近似值，再通过求极限得到其精准值。不过，这里“局部”的含义不同，求导数时的“局部”是在一点附近，而为引入定积分研究变速运动的路程或曲边梯形的面积时，研究的是在某区间内非均匀分布的量的整体和(图2)，要在所讨论的区间内采取“局部”近似。二者的差异是如何分别实现“局部”近似的问题。

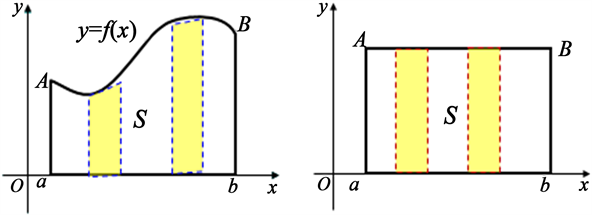
Figure 2. Comparison of non-uniformly distribution (left) & uniformly distribution (right)

图2. “非均匀分布的量”(左)与“均匀分布的量”(右)对比图

现以变速运动的路程问题为例，采用微积分基本思想，引入定积分。设某质点以速度 $v\left(t\right)$ 做变速直线运动，这里 $v\left(t\right)$ 是随时间t的变化而非均匀变化的连续量，求质点从时刻a到b所走过的路程。虽然“瞬时速度”与“路程”是截然不同的两个量，但研究的对象都是非均匀变化的变量，都应遵循微积分的基本思想方法，“局部”以“匀”代“非匀”，把“未知”(非匀速)转化为“已知”(匀速)。只不过研究运动质点在某时刻的瞬时速度是在这一点附近“局部”以“匀”代“非匀”，而现在要计算质点在整个时间区间 $\left[a,b\right]$ 内走过的路程。由于所求路程是 $\left[a,b\right]$ 上的可加量，为实现局部以匀代非匀，我们将 $\left[a,b\right]$ 分割为若干个长度很小的区间，在每个小区间内“局部”近似。为此，在 $\left[a,b\right]$ 内任意插入一串分点 $\left\{t_i\right\}$ ： $a=t_0<t_1<t_2<\cdots <t_{n-1}<t_n=b$，把 $\left[a,b\right]$ 分成n个小区间： $\left[t_0,t_1\right],\left[t_1,t_2\right],\cdots ,\left[t_{n-1},t_n\right]$ ；在每个小区间内以匀代非匀，把变速运动(“未知”)近似看作匀速运动(“已知”)；用“乘法”求出在每个小区间内路程的近似值 $v\left({\xi }_i\right)\cdot \Delta t_i$，再作和

${\displaystyle \underset{i=1}{\overset{n}{\sum }}v\left({\xi }_i\right)\Delta t_i}$

就得到在整个运动过程中路程的近似值。分割愈细，精确度愈高，因此，令所有小区间的长度趋于零，对该整体近似值求极限，就得到要求的路程。

研究由连续曲线 $y=f\left(x\right)\left(f\left(x\right)>0\right)$ 、直线 $x=a$ 、 $x=b$ 及x 轴所围成的曲边梯形的面积是为引入定积分所要研究的一个典型实例。注意到，曲线在区间 $\left[a,b\right]$ 上的变化是非均匀的，从而导致曲边梯形的面积在 $\left[a,b\right]$ 上的分布是非均匀的。因此，要研究的问题是“非均匀”分布的量的整体求和问题。遵循微积分的基本思想方法，应局部将面积分布“不均匀”这一“未知”转化为面积分布“均匀”这一“已知”。这使我们联想到熟知的矩形，矩形的面积分布是均匀的——底边上任意长度相同的线段所对应的矩形的面积都相等。因此，下面的问题就是局部将计算面积分布不均匀的曲边梯形面积转化为计算面积分布均匀的矩形面积。像上面对变速运动的路程的讨论那样，我们只需采取分割以实现“局部”替代；将每个小曲边梯形用矩形替代以将“未知”转化为“已知”；将所有小矩形面积相加得整体近似值；最后通过取极限得到面积的精准值。

将上述问题抽象为一般，就得到了定积分的定义。如果舍去最后的一步“精”，即不求极限，得到的就是近似值。为求其近似值，只需对曲边梯形进行“分、匀、合”三步。即将积分区间 $\left[a,b\right]$ 分成n个小区间 $\left[x_{i-1},x_i\right]$，从而相应地将整个曲边梯形分成n个小曲边梯形，对定积分作近似计算问题就是如何近似求出这些小曲边梯形的面积。遵循用“已知”解决“未知”的思想，我们用所熟悉的图形近似代替小曲边梯形。为此可以考虑用不同的直线段或抛物线来替代小曲边梯形的曲线弧，相应地就有了矩形法、梯形法与辛普森法等近似计算定积分的不同方法。它们都是用“已知”解决“未知”的具体应用，大大增加了学生对难点问题的理解程度。

总之，像把初等数学中为研究均匀变化的量的变化率所做的除法延伸到研究非均匀变化的量的变化率得到导数那样，定积分研究在一个区间非均匀分布的量的整体求和，需要将初等数学中为计算均匀分布的量的整体求和所做的乘法进行延伸。因此，导数与定积分可以分别看作初等数学中处理均匀量的商和积在处理相应的非均匀量中的发展延伸。

我们知道，定积分是学生学习的一大难点，其困难开始于为引出定积分而要讨论如上所述的计算曲边梯形的面积以及变速运动的路程(或变力做功)问题。在一般的教科书中，为计算曲边梯形的面积，往往都要围绕“变高”说为什么要分割、为什么要近似。其实说的越多，学生反而越感觉糊涂，产生一种似是而非的感觉。而利用微积分的基本思想来讨论这两个典型例子，简单、明了、清晰，教师容易讲，学生也容易接受，大大降低了教师讲授、学生学习的难度。微积分基本思想的揭示过程体现了用“已知的均匀”解决“未知的非均匀”这一基本思想的具体运用，不仅便于学生理解，而且可使学生领会微积分的精髓与真谛。

4. 微积分基本思想方法的应用

像引入定积分那样，研究非均匀分布在平面或空间中的几何体上的可加量的求和，都要遵循“用‘已知’认识‘未知’、研究‘未知’、解决‘未知’”的认知规则，利用微积分的基本思想方法，“局部”将非均匀分布的“未知”转化为均匀分布的“已知”，从而用初等方法求出其近似值，然后再取极限，就得到重积分、曲线积分或曲面积分等。

例如，一般为引入二重积分要讨论计算“曲顶柱体”的体积，它与“曲边梯形”的共性是“顶”都是曲的。因此，这自然使我们想到应采用讨论曲边梯形面积时所遵循的思想方法，将“曲顶柱体”这一“未知”转化为我们所熟悉的“已知”——平顶柱体。为此采取：分割、局部以匀(平)代非匀(曲)将“未知”转化为“已知”(图3左)，求出近似值，最后通过求极限就得到精准值。与计算曲边梯形面积不同的是，这里的差异只不过是分割的方法不同而已(图3右)。

Figure 3. Diagram of double integral

图3. 二重积分示意图

类似地，三重积分、对弧长的曲线积分与对面积的曲面积分等数值函数的积分也都根据微积分的基本思想方法得到。当然，对由向量值函数沿有向曲线或有向曲面产生的对坐标的曲线或曲面积分，除了需要“局部”将被积(向量值)函数“以匀代非匀”，还要将积分路径(曲线或曲面)“局部”用曲线的弦向量(或切向量)或有向曲面的切平面来近似替代，将要讨论的“未知”转化为“已知”的初等问题。

微积分的基本思想用在积分的应用中也使学生感到清晰易懂，便于使用。我们知道，如何求出微元是积分应用的关键。通常的教科书也给学生理解带来困难：如果要求的量U 的“部分量ΔU 的近似值能表示为 $\left[a,b\right]$ 上的连续函数在x处的值 $y=f\left(x\right)$ 与 $\text{d}x$ 的乘积，就把 $y=f\left(x\right)\text{d}x$ 称为量U 的元素(微元)”。可是 $y=f\left(x\right)$ 从何而来？我们并不知道。这实际并不能使学生明白“微元”应该怎样求得。但是，如果明确告诉学生：在 $\left[a,b\right]$ 上任取一微小区间 $\left[x,x+\text{d}x\right]$，在 $\left[x,x+\text{d}x\right]$ 上遵循微积分“以‘匀’代‘非匀’”的基本思想方法，将所研究的问题变成“已知”的初等问题，用初等方法求出ΔU的形如 $\text{d}U=f\left(x\right)\text{d}x$ 的近似值(实则是U 的微分)，就是要找的微元。

牛顿从物理学的角度导致了微积分的产生，事实上，微积分理论的基本思想是解决很多物理问题的极其重要的工具，通过对“极小”部分的物理过程的局部“以匀代非匀”进行分析、刻画，从而达到解决事物的整体。由实际问题建立微分方程也要利用微积分的基本思想方法，这是由于微分方程中一定含有导数，或函数的微分与自变量的微分。在物理、化学、工程科学、经济学、社会学等领域中大多数都会涉及到由微分方程建立的数学模型。在建立微分方程时，通过分析问题所涉及的原理或规律，找到涉及的各种量，确定自变量和因变量，若由实际问题能直接给出关于变化率的相关等式，则直接列出方程即可，若没有直接体现出变化率的等式，可通过微元法建立相关方程。像在积分的应用中建立微元那样在自变量的微小变化区间上，用微积分的基本思想局部“以匀代非匀”来分析问题所符合的规律建立局部量应满足的关系，进而得到全局关系式。

5. 结论

总之，揭示出微积分的基本思想，用它来引出微积分的基本概念和应用，是揭开微积分神秘的面纱，使学生学到微积分的真谛与精髓的最佳选择。同时也能大大降低教师讲授、学生接受微积分基本概念的难度。要使教师能在微积分的基本思想指导下讲授微积分，首先要在教材的编写中用微积分基本思想做指导，把这一思想明确地提出来，并应用在如上所述的各相关内容中，就能使微积分的教学难度大大降低，使得对微积分的概念教师难讲、学生难理解的状况得到根本缓解。

教材是包括教师备课、学生预习、教师讲课、学生课后复习这一整个教学系统的“根”。教材中要将用“已知”认识“未知”、用“已知”研究“未知”、用“已知”解决“未知”这一认知准则贯穿全书，引入新概念、证明新命题、求解例题，都着力引导学生探寻解决面临的“未知”所需要的“已知”，以培养学生正确的认知能力与科学的思维能力。使他们不仅知道“是什么”、“怎么做”，还知道“为什么”、“怎么想”，学到知识的精髓与真谛。教师也要依据这一规则讲课，层次清晰、逻辑严谨，使学生有恍然大悟、茅塞顿开的感觉，大大激发学习兴趣。

致谢

作者十分感激李伟教授的支持与指导。他通过多年的教学与科研的实践，总结出“用‘已知’认识‘未知’、用‘已知’研究‘未知’、用‘已知’解决‘未知’”的认知规则，用这一规则来看微积分的基本思想，就显得非常自然。

作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见。

基金项目

高等数学网络考试习题库的建设(2018JGYB022)，天津科技大学教育教学改革项目。

NOTES

^*通讯作者。