树和路字典积图的线性荫度

doi:10.12677/AAM.2022.1111865

期刊菜单

树和路字典积图的线性荫度
Linear Arboricity of Lexicographic Products of Trees and Paths

DOI: 10.12677/AAM.2022.1111865, PDF, HTML, XML, 国家自然科学基金支持
作者: 刘兆志, 买吐肉孜·买司地克^*：新疆师范大学数学科学学院，新疆乌鲁木齐
关键词: 线性荫度；笛卡尔积；直积；字典积；Linear Arboricity； Cartesian Product； Direct Product； Lexicographic Product

摘要: 近期，李确定了树T_m和路P_n的笛卡尔积图T_mWP_n、直积图T_m×P_n、强积图T_m)P_n的线性荫度，但其证明中漏掉了n=2的情况。本文先对以上三个乘积图的线性荫度补充n=2的证明，然后计算树和完全图的直积图以及树和路、路和树字典积图的线性荫度。

Abstract: Li has determined the linear arboricities of Cartesian product graph T_mWP_n , direct product graph T_m×P_n , and strong product graph T_m)P_n of tree T_m and path P_n recently, but their proofs left out the case n=2 . In this paper, we first supplement the proofs of n=2 to the linear arboricities of the above three product graphs, then we calculate the linear arboricities of the direct product of tree and complete graph, and the lexicographic products of tree and path and path and tree.

文章引用：刘兆志, 买吐肉孜·买司地克. 树和路字典积图的线性荫度[J]. 应用数学进展, 2022, 11(11): 8171-8182. https://doi.org/10.12677/AAM.2022.1111865

1. 引言

本文只涉及非平凡简单无向图 $G = (V (G), E (G))$ 。每个连通分支均为路的图称为线性森林。1970年，Harary [1] 最先提出图G线性荫度 $l a (G)$ 的概念： $l a (G) = \min$ { $k : E (G)$ 划分成k个部分使得每个部分导出的图是线性森林}。显然在图G的边集 $E (G)$ 分解为边不交的线性森林中，每个顶点的度至多为2，因而有 $l a (G) \geq ⌈ \frac{Δ (G)}{2} ⌉$ ，其中 $Δ (G)$ 表示图G的最大度。不引起混淆时 $Δ$ 表示最大度。

1980年Akiyama [2] 等人提出线性荫度猜想 $⌈ \frac{Δ (G)}{2} ⌉ \leq l a (G) \leq ⌈ \frac{Δ (G) + 1}{2} ⌉$ ，并且证明了树，完全图，完全二部图，以及 $Δ = 3$ 的图满足线性荫度猜想。一年后，他们又证明了 $Δ = 4$ 的图满足线性荫度猜想 [3]。1984年，Enomoto [4] 等人证明了 $Δ = 5, 6, 8$ 的图满足线性荫度猜想。1986年，Guldan [5] 证明了 $Δ = 10$ 的图满足线性荫度猜想。1999年，Wu [6] 证明了 $Δ \geq 9$ 的平面图满足线性荫度猜想，2008年，Wu [7] 等人证明了 $Δ = 7$ 的平面图满足线性荫度猜想。

本文研究一些特殊图类乘积图的线性荫度，下面介绍本文涉及四种乘积图的常见定义。

定义1.图G和图H的笛卡尔积 $G □ H$ ：顶点集为 ${(u, v) | u \in V (G), v \in V (H)}$ ，边集为 ${(u, v) (u^{'}, v^{'}) | v = v^{'} 且 u u^{'} \in E (G) 或 u = u^{'} 且 v v^{'} \in E (H)}$ 。

定义2.图G和图H的直积 $G \times H$ ：顶点集为 ${(u, v) | u \in V (G), v \in V (H)}$ ，边集为 ${(u, v) (u^{'}, v^{'}) | u u^{'} \in E (G), v v^{'} \in E (H) 或 u v^{'} \in E (G), v u^{'} \in E (H)}$ 。

定义3.图G和图H的强积图 $G ⊠ H$ ：顶点集为 ${(u, v) | u \in V (G), v \in V (H)}$ ，边集 $E (G ⊠ H) = E (G □ H) \cup E (G \times H)$ 。

定义4.图G和图H的字典积 $G [H]$ ：顶点集为 ${(u, v) | u \in V (G), v \in V (H)}$ ，边集为 ${(u, v) (u^{'}, v^{'}) | u u^{'} \in E (G) 或 u = u^{'} 且 v v^{'} \in E (H)}$ 。

引理1. [2] 树T的线性荫度 $l a (T) = ⌈ \frac{Δ (T)}{2} ⌉$ 。

引理2. [2] 完全二部图 $K_{m, n}$ ( $m \geq n$ )的线性荫度 $l a (K_{m, n}) = ⌈ \frac{m + δ (m, n)}{2} ⌉$ ，其中 $δ (m, n) = {\begin{matrix} \begin{matrix} 0, & m \neq n; \end{matrix} \\ \begin{matrix} 1, & m = n . \end{matrix} \end{matrix}$ 。

文献 [8] 给出了树与路笛卡尔积，直积，强积的线性荫度，但漏了路是两个顶点的情况，下面依次给予补充。下列结论的证明中需要一些新术语。由引理1，在树T的任意一种满足 $l a (T)$ 的线性森林划分中，每个最大度顶点至多在一个划分中以路的端点的形式出现，其余划分中以路的内部顶点的形式出现。现要求树T满足 $l a (T)$ 划分中的每个分支只能以至多一个最大度顶点为端点，若有一个分支的两个端点都为最大度顶点，可将此分支的任意一端延长至延长端的端点不是最大度顶点为止，此操作下新加入的边在原分支中删除即可，从而保证新的划分仍是树T满足 $l a (T)$ 的线性森林划分，本文将此类树T划分称为第一类划分。

引理3. m个顶点的树 $T_{m}$ 与n个顶点的路 $P_{n}$ 笛卡尔积的线性荫度

$l a (T_{m} □ P_{n}) = {\begin{array}{l} ⌈ \frac{Δ (T_{m} □ P_{n}) + 1}{2} ⌉, & Δ (T_{m}) = 1, n = 2; \\ ⌈ \frac{Δ (T_{m} □ P_{n})}{2} ⌉, & 其它 . \end{array}$

证明. 设 $V (T_{m}) = {u_{1}, u_{2}, \dots, u_{m}}$ ， $P_{n} = v_{1} v_{2} \dots v_{n}$ 。当 $n > 2$ 时，有 $l a (T_{m} □ P_{n}) = ⌈ \frac{Δ (T_{m} □ P_{n})}{2} ⌉$ ，将图 $T_{m} □ P_{n}$ 看作树 $T_{m}$ 的n个互不交拷贝与路 $P_{n}$ 的m个拷贝的并，树 $T_{m}$ 的线性森林划分加上路 $P_{n}$ 的线性森林划分就可得到满足 $l a (T_{m} □ P_{n})$ 的 $T_{m} □ P_{n}$ 的线性森林划分。具体证明过程看文献 [8]。下面设 $n = 2$ 。

显然有 $Δ (P_{2}) = 1$ ，由定义1得， $Δ (T_{m} □ P_{2}) = Δ (T_{m}) + 1$ ，从而 $l a (T_{m} □ P_{2}) \geq ⌈ \frac{Δ (T_{m} □ P_{2})}{2} ⌉ = ⌈ \frac{Δ (T_{m}) + 1}{2} ⌉$ 。

当 $Δ (T_{m}) = 1$ 时，有 $T_{m} □ P_{2} = C_{4}$ (四长的圈)，所以 $l a (T_{m} □ P_{2}) = ⌈ \frac{Δ (T_{m} □ P_{2}) + 1}{2} ⌉$ 。

当 $Δ (T_{m}) \geq 2$ 时，分以下两种情况：

$Δ (T_{m}) \equiv 1 (\mod 2)$ 时，图 $T_{m} □ P_{2}$ 可以看作树 $T_{m}$ 的两个拷贝及其对应边组成的，这里对应边指的是 $(u_{i}, v_{1}) (u_{i}, v_{2})$ ( $i = 1, 2, \dots, m$ )。先考虑树 $T_{m}$ 的一个拷贝与所有对应边组成的图 $G^{'} = T_{m} \cup {(u_{i}, v_{1}) (u_{i}, v_{2}) | i = 1, 2, \dots, m}$ ，采用树 $T_{m}$ 的第一类划分，此时将所有以最大度顶点为分支端点的对应边添加到树 $T_{m}$ 的分支中，得到的划分还是线性森林，再将剩余对应边添加到不包含对应边端点的划分中作为新的分支，让 $T_{m}$ 的另一拷贝的划分与前一个拷贝的划分相同，再将相同的划分合成新的划分，则得到的划分既是 $T_{m} □ P_{2}$ 的划分也是线性森林，所以 $l a (T_{m} □ P_{2}) = ⌈ \frac{Δ (T_{m})}{2} ⌉ = ⌈ \frac{Δ (T_{m} □ P_{2})}{2} ⌉$ 。

$Δ (T) \equiv 0 (\mod 2)$ 时，最大度顶点的对应边只能作为新划分，从而 $l a (T_{m} □ P_{2}) = ⌈ \frac{Δ (T_{m})}{2} ⌉ + 1 = ⌈ \frac{Δ (T_{m} □ P_{2})}{2} ⌉$ 。□

引理4. [8] m个顶点的树 $T_{m}$ 与n个顶点的路 $P_{n}$ 直积的线性荫度 $l a (T_{m} \times P_{n}) = ⌈ \frac{Δ (T_{m} \times P_{n})}{2} ⌉$ 。

证明. 设 $V (T_{m}) = {u_{1}, u_{2}, \dots, u_{m}}$ ， $P_{n} = v_{1} v_{2} \dots v_{n}$ 。当 $n > 2$ 时，由文献 [8] 得 $l a (T_{m} \times P_{n}) = ⌈ \frac{Δ (T_{m} \times P_{n})}{2} ⌉$ 。下面设 $n = 2$ 。由定义2，图 $T_{m} \times P_{2}$ 可看作两个树 $T_{m}$ 拷贝的不交并，由引理1得， $l a (T_{m} \times P_{2}) = ⌈ \frac{Δ (T_{m})}{2} ⌉ = ⌈ \frac{Δ (T_{m} \times P_{2})}{2} ⌉$ 。□

由引理3和4及树 $T_{m}$ 与路 $P_{n}$ 的强积图 $T_{m} ⊠ P_{n} = (T_{m} □ P_{n}) \cup (T_{m} \times P_{n})$ ，可知 $l a (T_{m} ⊠ P_{n}) \leq l a (T_{m} □ P_{n}) + l a (T_{m} \times P_{n})$ 成立，而 $Δ (T_{m} ⊠ P_{n}) = Δ (T_{m} □ P_{n}) + Δ (T_{m} \times P_{n})$ ，故有定理1。

定理1. [8] m个顶点的树 $T_{m}$ 与n个顶点的路 $P_{n}$ 强积图的线性荫度 $l a (T_{m} ⊠ P_{n}) = ⌈ \frac{Δ (T_{m} ⊠ P_{n})}{2} ⌉$ 。

证明. 设 $V (T_{m}) = {u_{1}, u_{2}, \dots, u_{m}}$ ， $P_{n} = v_{1} v_{2} \dots v_{n}$ 。当 $n > 2$ 时，由文献 [8] 得 $l a (T_{m} ⊠ P_{n}) = ⌈ \frac{Δ (T_{m} ⊠ P_{n})}{2} ⌉$ 。下面设 $n = 2$ 。

由定义3得， $Δ (T_{m} ⊠ P_{2}) = 2 Δ (T_{m}) + 1$ ，则 $l a (T_{m} ⊠ P_{2}) \geq ⌈ \frac{Δ (T_{m} ⊠ P_{2})}{2} ⌉ = Δ (T_{m}) + 1$ 。

当 $Δ (T_{m}) = 1$ 时，因为能用以下两个线性森林覆盖 $T_{m} ⊠ P_{2}$ ：

$L F_{1} = (u_{1}, v_{1}) (u_{1}, v_{2}) (u_{2}, v_{1}) (u_{2}, v_{2})$ ; $L F_{2} = (u_{2}, v_{1}) (u_{1}, v_{1}) (u_{2}, v_{2}) (u_{1}, v_{2})$ .

所以 $l a (T_{m} ⊠ P_{2}) \leq 2$ ，又 $l a (T_{m} ⊠ P_{2}) \geq 2$ ，所以 $l a (T_{m} ⊠ P_{2}) = 2 = ⌈ \frac{Δ (T_{m} ⊠ P_{2})}{2} ⌉$ 。

当 $Δ (T_{m}) \geq 2$ 时， $l a (T_{m} ⊠ P_{2}) \leq ⌈ \frac{Δ (T_{m}) + 1}{2} ⌉ + ⌈ \frac{Δ (T_{m})}{2} ⌉ = Δ (T_{m}) + 1$ 。故 $l a (T_{m} ⊠ P_{2}) = ⌈ \frac{Δ (T_{m} ⊠ P_{2})}{2} ⌉$ 。□

2. 主要结果及证明

本文的主要结果是乘积图 $T_{m} \times K_{n}$ ， $T_{m} [P_{n}]$ 和 $P_{m} [T_{n}]$ 的线性荫度的确定。由定义1，2，4可以观察到： $T_{m} [P_{n}] = (T_{m} □ P_{n}) \cup (T_{m} \times K_{n})$ 。

2.1. 树与完全图直积的线性荫度

定理2. $l a (T_{m} \times K_{n}) = {\begin{array}{l} ⌈ \frac{Δ (T_{m} \times K_{n}) + 1}{2} ⌉, & Δ (T_{m}) = 1, n > 2, n \equiv 1 (\mod 2); \\ ⌈ \frac{Δ (T_{m} \times K_{n})}{2} ⌉, & 其它 . \end{array}$

证明. 设 $V (T_{m}) = {u_{1}, u_{2}, \dots, u_{m}}$ ， $V (K_{n}) = {v_{1}, v_{2}, \dots, v_{n}}$ 。由定义2得， $Δ (T_{m} \times K_{n}) = Δ (T_{m}) (n - 1)$ 。

以下分三种情况：

情况一. $Δ (T_{m}) = 1$ ， $n = 2$ 。

由引理4得， $l a (T_{m} \times K_{2}) = ⌈ \frac{Δ (T_{m} \times K_{2})}{2} ⌉$ 。

情况二. $Δ (T_{m}) = 1$ ， $n > 2$ 。

由 $T_{m} = P_{2} = u_{1} u_{2}$ 得， $l a (P_{2} \times K_{n}) \geq ⌈ \frac{n - 1}{2} ⌉$ 。现将 $E (P_{2} \times K_{n})$ 划分为 $2 (n - 1)$ 个集合：即对正整数 $2 \leq k \leq n$ ，有

$Y_{k}^{1} = {(u_{1}, v_{j}) (u_{2}, v_{j + (k - 1)}) | j = 1, 2, \dots, n - (k - 1)}$ ;

$Y_{k}^{2} = {(u_{2}, v_{j}) (u_{1}, v_{j + (k - 1)}) | j = 1, 2, \dots, n - (k - 1)}$ .

当 $n \equiv 0 (\mod 2)$ 时， $l a (P_{2} \times K_{n}) \geq \frac{n}{2}$ 。易验证，任意正整数 $2 \leq s \leq n - 1$ ， $Y_{2 ⌊ \frac{s}{2} ⌋}^{i} \cup Y_{2 ⌊ \frac{s}{2} ⌋ + 1}^{i}$ ( $i = 1, 2$ )导出的图是路，顶点集

$\begin{matrix} D_{2 ⌊ \frac{s}{2} ⌋} = V (P_{2} \times K_{n}) ∖ V (Y_{2 ⌊ \frac{s}{2} ⌋}^{i} \cup Y_{2 ⌊ \frac{s}{2} ⌋ + 1}^{i}) \\ = {\begin{matrix} {(u_{2}, v_{j}) | j = 1, 2, \dots, 2 ⌊ \frac{s}{2} ⌋ - 1} \cup {(u_{1}, v_{j}) | j = n - 2 ⌊ \frac{s}{2} ⌋ + 2, \dots, n}, & i = 1; \\ {(u_{1}, v_{j}) | j = 1, 2, \dots, 2 ⌊ \frac{s}{2} ⌋ - 1} \cup {(u_{2}, v_{j}) | j = n - 2 ⌊ \frac{s}{2} ⌋ + 2, \dots, n}, & i = 2. \end{matrix} \end{matrix}$

又 $i = 1$ 时顶点集 $D_{2 ⌊ \frac{s}{2} ⌋}$ 与图 $Y_{n + 2 - 2 ⌊ \frac{s}{2} ⌋}^{2} \cup Y_{n + 3 - 2 ⌊ \frac{s}{2} ⌋}^{2}$ 的顶点集相同； $i = 2$ 时顶点集 $D_{2 ⌊ \frac{s}{2} ⌋}$ 与图 $Y_{n + 2 - 2 ⌊ \frac{s}{2} ⌋}^{1} \cup Y_{n + 3 - 2 ⌊ \frac{s}{2} ⌋}^{1}$ 的顶点集相同。当 $4 \leq s \leq n - 1$ 时，

$Y_{2 ⌊ \frac{s}{2} ⌋}^{1} \cup Y_{2 ⌊ \frac{s}{2} ⌋ + 1}^{1} \cup Y_{n + 2 - 2 ⌊ \frac{s}{2} ⌋}^{2} \cup Y_{n + 3 - 2 ⌊ \frac{s}{2} ⌋}^{2}$ 与 $Y_{2 ⌊ \frac{s}{2} ⌋}^{2} \cup Y_{2 ⌊ \frac{s}{2} ⌋ + 1}^{2} \cup Y_{n + 2 - 2 ⌊ \frac{s}{2} ⌋}^{1} \cup Y_{n + 3 - 2 ⌊ \frac{s}{2} ⌋}^{1}$

都是路的不交并，当 $s = 2, 3$ 时， $Y_{2}^{1} \cup Y_{3}^{1} \cup Y_{n}^{2}$ 与 $Y_{2}^{2} \cup Y_{3}^{2} \cup Y_{n}^{1}$ 也是路的不交并。令 $L F_{1} = Y_{2}^{1} \cup Y_{3}^{1} \cup Y_{n}^{2}$ ， $L F_{2} = Y_{2}^{2} \cup Y_{3}^{2} \cup Y_{n}^{1}$ ，当正整数 $3 \leq l \leq \frac{n}{2}$ 时，

$L F_{l} = {\begin{array}{l} Y_{2 ⌊ \frac{l + 1}{2} ⌋}^{1} \cup Y_{2 ⌊ \frac{l + 1}{2} ⌋ + 1}^{1} \cup Y_{n + 2 - 2 ⌊ \frac{l + 1}{2} ⌋}^{2} \cup Y_{n + 3 - 2 ⌊ \frac{l + 1}{2} ⌋}^{2}, & l \equiv 1 (\mod 2); \\ Y_{2 ⌊ \frac{l}{2} ⌋}^{2} \cup Y_{2 ⌊ \frac{l}{2} ⌋ + 1}^{2} \cup Y_{n + 2 - 2 ⌊ \frac{l}{2} ⌋}^{1} \cup Y_{n + 3 - 2 ⌊ \frac{l}{2} ⌋}^{1}, & l \equiv 0 (\mod 2) . \end{array}$

从而 $L F_{l}$ ( $1 \leq l \leq \frac{n}{2}$ )是 $P_{2} \times K_{n}$ 的线性森林划分，故 $l a (P_{2} \times K_{n}) = \frac{n}{2} = ⌈ \frac{Δ (P_{2} \times K_{n})}{2} ⌉$ 。图1所示为图 $P_{2} \times K_{6}$ 的线性森林划分。

Figure 1. Graph $L F_{1}$ (left), graph $L F_{2}$ (center), graph $L F_{3}$ (right), where the vertex $(u_{i}, v_{j})$ is simply denoted by ij

图1. 图 $L F_{1}$ (左)，图 $L F_{2}$ (中)，图 $L F_{3}$ (右)。图中将顶点 $(u_{i}, v_{j})$ 简写为ij

当 $n \equiv 1 (\mod 2)$ 时， $l a (P_{2} \times K_{n}) \geq \frac{n - 1}{2}$ 。易验证，对任意 $2 \leq k \leq n$ ， $Y_{2 ⌊ \frac{k}{2} ⌋}^{i} \cup Y_{2 ⌊ \frac{k}{2} ⌋ + 1}^{i}$ ( $i = 1, 2$ )组成的图是一条路。对任意正整数 $4 \leq t \leq n$ ，顶点集

$\begin{matrix} D_{2 ⌊ \frac{t}{2} ⌋} = V (P_{2} \times K_{n}) ∖ V (Y_{2 ⌊ \frac{t}{2} ⌋}^{i} \cup Y_{2 ⌊ \frac{t}{2} ⌋ + 1}^{i}) \\ = {\begin{matrix} {(u_{2}, v_{j}) | j = 1, 2, \dots, 2 ⌊ \frac{t}{2} ⌋ - 2} \cup {(u_{1}, v_{j}) | j = n_{2} - 2 ⌊ \frac{t}{2} ⌋ + 3, \dots, n}, & i = 1; \\ {(u_{1}, v_{j}) | j = 1, 2, \dots, 2 ⌊ \frac{t}{2} ⌋ - 2} \cup {(u_{2}, v_{j}) | j = n_{2} - 2 ⌊ \frac{t}{2} ⌋ + 3, \dots, n}, & i = 2. \end{matrix} \end{matrix}$

又 $i = 1$ 时顶点集 $D_{2 ⌊ \frac{t}{2} ⌋}$ 与图 $Y_{n + 3 - 2 ⌊ \frac{t}{2} ⌋}^{2} \cup Y_{n + 4 - 2 ⌊ \frac{t}{2} ⌋}^{2}$ 的顶点集相同； $i = 2$ 时顶点集 $D_{2 ⌊ \frac{t}{2} ⌋}$ 与图 $Y_{n + 3 - 2 ⌊ \frac{t}{2} ⌋}^{1} \cup Y_{n + 4 - 2 ⌊ \frac{t}{2} ⌋}^{1}$ 的顶点集相同。从而对正整数 $4 \leq t \leq n$ ，

$Y_{2 ⌊ \frac{t}{2} ⌋}^{1} \cup Y_{2 ⌊ \frac{t}{2} ⌋ + 1}^{1} \cup Y_{n + 3 - 2 ⌊ \frac{t}{2} ⌋}^{2} \cup Y_{n + 4 - 2 ⌊ \frac{t}{2} ⌋}^{2}$ 与 $Y_{2 ⌊ \frac{t}{2} ⌋}^{2} \cup Y_{2 ⌊ \frac{t}{2} ⌋ + 1}^{2} \cup Y_{n + 3 - 2 ⌊ \frac{t}{2} ⌋}^{1} \cup Y_{n + 4 - 2 ⌊ \frac{t}{2} ⌋}^{1}$

都是路的不交并，当 $k = 2, 3$ 时， $Y_{2}^{1} \cup Y_{3}^{1}$ 与 $Y_{2}^{2} \cup Y_{3}^{2}$ 也是路的不交并。此时令 $L F_{1} = Y_{2}^{1} \cup Y_{3}^{1}$ ， $L F_{2} = Y_{2}^{2} \cup Y_{3}^{2}$ ，当正整数 $3 \leq r \leq \frac{n + 1}{2}$ 时，

$L F_{r} = {\begin{array}{l} Y_{2 ⌊ \frac{r + 1}{2} ⌋}^{1} \cup Y_{2 ⌊ \frac{r + 1}{2} ⌋ + 1}^{1} \cup Y_{n + 3 - 2 ⌊ \frac{r + 1}{2} ⌋}^{2} \cup Y_{n + 4 - 2 ⌊ \frac{r + 1}{2} ⌋}^{2}, & r \equiv 1 (\mod 2); \\ Y_{2 ⌊ \frac{r}{2} ⌋}^{2} \cup Y_{2 ⌊ \frac{r}{2} ⌋ + 1}^{2} \cup Y_{n + 3 - 2 ⌊ \frac{r}{2} ⌋}^{1} \cup Y_{n + 4 - 2 ⌊ \frac{r}{2} ⌋}^{1}, & r \equiv 0 (\mod 2) . \end{array}$

因此 $L F_{r}$ ( $1 \leq r \leq \frac{n + 1}{2}$ )是 $P_{2} \times K_{n}$ 的线性森林划分，从而 $l a (P_{2} \times K_{n}) \leq \frac{n + 1}{2}$ 。下证 $l a (P_{2} \times K_{n}) = \frac{n + 1}{2}$ 。

假设 $l a (P_{2} \times K_{n}) = \frac{n - 1}{2}$ ，因图 $P_{2} \times K_{n}$ 是 $(n - 1)$ -正则图且 $n - 1 = 2 (\frac{n - 1}{2})$ ，即在每个线性森林划分中每个顶点的度为2，因而每个划分不是森林，与线性荫度定义矛盾。从而 $l a (P_{2} \times K_{n}) = ⌈ \frac{Δ (P_{2} \times K_{n}) + 1}{2} ⌉$ 。

情况三. $Δ (T_{m}) \geq 2$ ， $n \geq 2$ 。

此时 $l a (T_{m} \times K_{n}) \geq ⌈ \frac{Δ (T_{m}) (n - 1)}{2} ⌉ = {\begin{array}{l} \begin{matrix} \frac{Δ (T_{m}) (n - 1)}{2}, & Δ (T_{m}) \equiv 0 (\mod 2); \end{matrix} \\ \begin{matrix} \frac{Δ (T_{m}) (n - 1)}{2}, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2); \end{matrix} \\ \begin{matrix} \frac{Δ (T_{m}) (n - 1) + 1}{2}, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2) . \end{matrix} \end{array}$

首先考虑图 $P_{a} \times K_{n} (a \geq 2)$ 的一种划分：现将 $E (P_{a} \times K_{n})$ 划分为 $2 (n - 1)$ 个集合，对正整数 $k \in [2, n]$

$\begin{array}{l} X_{k}^{1} = {(u_{i}, v_{j}) (u_{i + 1}, v_{j + k - 1}) | i = 1,3, \dots, (⌊ \frac{a + 1}{2} ⌋ + ⌊ \frac{a - 1}{2} ⌋); j = 1, 2, \dots, n - k + 1} \\ \cup {(u_{i}, v_{j}) (u_{i + 1}, v_{j - k + 1}) | i = 2,4, \dots, 2 ⌊ \frac{a}{2} ⌋; j = k, k + 1, \dots, n}; \end{array}$

$\begin{array}{l} X_{k}^{2} = {(u_{i}, v_{j}) (u_{i + 1}, v_{j - k + 1}) | i = 1, 3, \dots, (⌊ \frac{a + 1}{2} ⌋ + ⌊ \frac{a - 1}{2} ⌋); j = k, k + 1, \dots, n} \\ \cup {(u_{i}, v_{j}) (u_{i + 1}, v_{j + k - 1}) | i = 2, 4, \dots, 2 ⌊ \frac{a}{2} ⌋; j = 1, 2, \dots, n - k + 1} . \end{array}$

易验证， $X_{k}^{1}$ 与 $X_{k}^{2}$ 的分支都是 $P_{a}$ 的拷贝。对 $b = 1, 2, \dots, n - 1$ ，令 $L F_{b} = {\begin{matrix} X_{⌈ \frac{b}{2} ⌉ + 1}^{1} \cup X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{2}, & b \equiv 1 (\mod 2); \\ X_{⌈ \frac{b}{2} ⌉ + 1}^{2} \cup X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{1}, & b \equiv 0 (\mod 2) . \end{matrix}$

$a = 2$ 时，图 $P_{a} \times K_{n}$ 的线性荫度在情况一和情况二中已经讨论过。下面讨论 $a > 2$ 时，图 $P_{a} \times K_{n}$ 的线性荫度。

当 $b \equiv 1 (\mod 2)$ 时，图 $X_{⌈ \frac{b}{2} ⌉ + 1}^{1}$ 与图 $X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{2}$ 是顶点集不交的，因为 $X_{⌈ \frac{b}{2} ⌉ + 1}^{1}$ 与 $X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{2}$ 都是路，从而 $L F_{b} = X_{⌈ \frac{b}{2} ⌉ + 1}^{1} \cup X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{2}$ 是线性森林。同理，当 $b \equiv 0 (\mod 2)$ 时， $L F_{i} = X_{⌈ \frac{b}{2} ⌉ + 1}^{2} \cup X_{n + 1 - ⌈ \frac{b}{2} ⌉}^{1}$ 也是线性森林。又 $\cup_{b = 1}^{n - 1} L F_{b} = \cup_{k = 2}^{n} X_{k}^{1} \cup_{k = 2}^{n} X_{k}^{2} = E (P_{a} \times K_{n})$ 。故 $L F_{b}$ ( $b = 1, 2, \dots, n - 1$ )是 $P_{a} \times K_{n}$ 的一种线性森林划分，则 $l a (P_{a} \times K_{n}) \leq n - 1$ 。从而 $l a (P_{a} \times K_{n}) = n - 1 = ⌈ \frac{Δ (P_{a} \times K_{n})}{2} ⌉$ 。

然后考虑图 $T_{m} \times K_{n}$ 的一种划分：首先在树 $T_{m}$ 中任意选取一个叶子点作为起点(设为f)，以距离最近(距离非零)的原树 $T_{m}$ 的分支点(本文将树中度大于2的顶点称为树的分支点)为终点取路P，否则以另一个叶子点为终点取路P。得到新的树 $T^{'} = T_{m} \ E (P)$ 。再以上一次的终点为新起点，以同样的方法选取图 $T^{'}$ 中的终点得到新的路P，直到图 $T^{'}$ 为空图。显然这些路P的并是原图树 $T_{m}$ 。如图2所示，树 $T_{6}$ 中取路的起点选作 $u_{1}$ ，数字1，2，3代表取路的顺序。

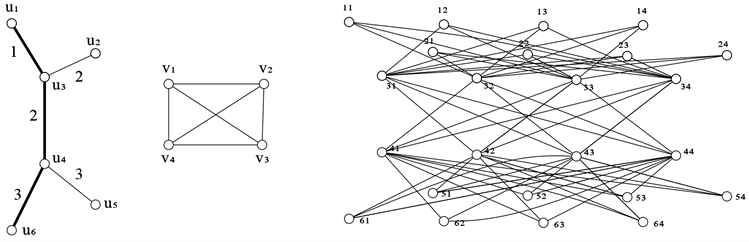
Figure 2. A tree $T_{6}$ (left), the complete graph $K_{4}$ (center), and their direct product $T_{6} \times K_{4}$ (right)

图2. 树 $T_{6}$ (左)与完全图 $K_{4}$ (中)的直积图 $T_{6} \times K_{4}$ (右)

本文将以树T中最大度顶点为端点的路长为1的分支称为单分支，若树T满足 $Δ (T) \equiv 1 (\mod 2)$ ，则所有单分支的并（必定为不交并）可作为一个划分。若第一类划分中除单分支外的其它划分分支的端点不是最大度顶点，则此划分为第二类划分。如图3所示，粗实线与实线为树的两个线性森林，右侧图中粗实线表示单分支。

Figure 3. A first (left) and second (right) divisions of a tree

图3. 树的第一类划分(左)与第二类划分(右)

在图 $T_{m} \times K_{n}$ 中选取点 ${(f, v_{j}) | j = 1, 2, \dots, n}$ 作为起点，将上述 $L F_{b}$ 的选取方式以及树T中路P的选取方式得到的图记为 $L T_{b}$ ( $b = 1, 2, \dots, n - 1$ )，则图 $L T_{b}$ 中的分支都是树 $T_{m}$ 的拷贝。令树 $T_{m}$ 的所有拷贝采用完全相同的第二类划分，则 $l a (T_{m}) = ⌈ \frac{Δ (T_{m})}{2} ⌉$ ，又 $E (T_{m} \times K_{n}) = \cup_{b = 1}^{n - 1} L T_{b}$ ，所以

$l a (T_{m} \times K_{n}) \leq (n - 1) l a (T_{m}) = {\begin{array}{l} \frac{(n - 1) Δ (T_{m})}{2}, & Δ (T_{m}) \equiv 0 (\mod 2); \\ \frac{(n - 1) (Δ (T_{m}) + 1)}{2}, & Δ (T_{m}) \equiv 1 (\mod 2) . \end{array}$

$Δ (T_{m}) \equiv 1 (\mod 2)$ 时，将每个图 $L T_{b}$ 中单分支组成的图记为 $L C_{b}$ ( $b = 1, 2, \dots, n - 1$ )，令 $L C = \cup_{b = 1}^{n - 1} L C_{b}$ ，则图LC中每个分支都是 $P_{2} \times K_{n}$ 的拷贝。现图 $T_{m} \times K_{n}$ 中除 $L C$ 外不改变划分方式， $L C$ 改为图 $P_{2} \times K_{n}$ 的满足线性荫度的划分方式。由情况一和情况二可知，当 $n \equiv 1 (\mod 2)$ 时，图 $T_{m} \times K_{n}$ 的总划分数中将减少 $\frac{n - 1}{2}$ 个划分，从而 $l a (T_{m} \times K_{n}) = \frac{(n - 1) (Δ (T_{m}) + 1)}{2} - \frac{n - 1}{2} = \frac{(n - 1) Δ (T_{m})}{2}$ 。当 $n \equiv 0 (\mod 2)$ 时，图 $T_{m} \times K_{n}$ 的总划分数中将减少 $\frac{n - 2}{2}$ 个划分，从而 $l a (T_{m} \times K_{n}) = \frac{(n - 1) (Δ (T_{m}) + 1)}{2} - \frac{n - 2}{2} = \frac{(n - 1) Δ (T_{m}) + 1}{2}$ 。

故 $l a (T_{m} \times K_{n}) = ⌈ \frac{Δ (T_{m}) \cdot (n - 1)}{2} ⌉ = ⌈ \frac{Δ (T_{m} \times K_{n})}{2} ⌉$ 。□

例如图 $T_{6} \times K_{4}$ 中，树 $T_{6}$ 的划分如图2(左)所示中实粗线与实线，树 $T_{6}$ 中单分支是实线，以 $L F_{b}$ 的选取方式以及树T中路P的选取方式得到的图(如图4所示)为 $L T_{1}$ ， $L T_{2}$ ， $L T_{3}$ 。进而图 $T_{6} \times K_{4}$ 的线性森林有6个，在保持其它划分不变的情况下重新计算图LC的线性荫度，而 $l a (L C) = 2$ ，其它划分为3，从而 $l a (T_{6} \times K_{4}) = 5$ ，即减少1个划分。

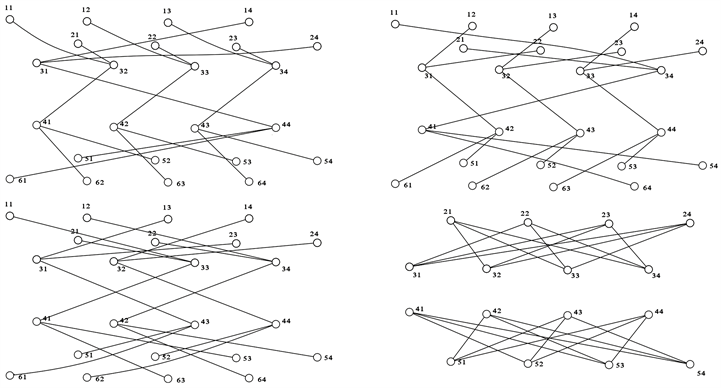
Figure 4. Graph $L T_{1}$ (top left), graph $L T_{2}$ (top right), graph $L T_{3}$ (bottom left), graph $L C$ (bottom right)

图4. 图 $L T_{1}$ (左上)，图 $L T_{2}$ (右上)，图 $L T_{3}$ (左下)，图 $L C$ (右下)

2.2. 树与路字典积的线性荫度

定理3. $Δ (T_{m}) = 1$ ， $n > 2$ ， $n \equiv 0 (\mod 2)$ 时， $l a (T_{m} [P_{n}]) = ⌈ \frac{Δ (T_{m} [P_{n}]) + 1}{2} ⌉$ ；

$Δ (T_{m}) \geq 2$ ， $Δ (T_{m}) \equiv 1 (\mod 2)$ ， $n > 2$ ， $n \equiv 0 (\mod 2)$ 时， $⌈ \frac{Δ (T_{m} [P_{n}])}{2} ⌉ \leq l a (T_{m} [P_{n}]) \leq ⌈ \frac{Δ (T_{m} [P_{n}]) + 1}{2} ⌉$ ；

其它条件时， $l a (T_{m} [P_{n}]) = ⌈ \frac{Δ (T_{m} [P_{n}])}{2} ⌉$ 。

证明. 设 $V (T_{m}) = {u_{1}, u_{2}, \dots, u_{m}}$ ， $P_{n} = v_{1} v_{2} \dots v_{n}$ 。由定义4得 $Δ (T_{m} [P_{n}]) = Δ (T_{m}) n + Δ (P_{n})$ 。以下分四种情况：

情况一. $Δ (T_{m}) = 1$ ， $n = 2$ 。

这时 $T_{m} = P_{2} = u_{1} u_{2}$ ，因 $T_{m} [P_{2}] = P_{2} [P_{2}] = P_{2} ⊠ P_{2} = T_{m} ⊠ P_{2}$ ，由定理1， $l a (T_{m} [P_{2}]) = ⌈ \frac{Δ (T_{m} [P_{2}])}{2} ⌉$ 。

情况二. $Δ (T_{m}) = 1$ ， $n > 2$ 。

这时 $T_{m} = P_{2} = u_{1} u_{2}$ ，因 $Δ (P_{n}) = 2$ ，得 $l a (P_{2} [P_{n}]) \geq ⌈ \frac{Δ (P_{2} [P_{n}])}{2} ⌉ = ⌈ \frac{n}{2} ⌉ + 1$ 。

显然 $P_{2} [P_{n}] = K_{n, n} \cup {(u_{i}, v_{j}) (u_{i}, v_{j + 1}) | i = 1, 2; j = 1, 2, \dots, n - 1}$ ，显然后者是由两条不交路组成的图，从而 $l a ({(u_{i}, v_{j}) (u_{i}, v_{j + 1}) | i = 1, 2; j = 1, 2, \dots, n - 1}) = 1$ 。由引理2得， $l a (K_{n, n}) = ⌈ \frac{n + 1}{2} ⌉$ ，从而

$l a (P_{2} [P_{n}]) \leq l a (K_{n, n}) + l a ({(u_{i}, v_{j}) (u_{i}, v_{j + 1}) | i = 1, 2; j = 1, 2, \dots, n - 1}) = ⌈ \frac{n + 1}{2} ⌉ + 1$ ,

又 $l a (P_{2} [P_{n}]) \geq ⌈ \frac{n}{2} ⌉ + 1$ ，所以

当 $n \equiv 1 (\mod 2)$ 时，上式取等号，此时 $l a (P_{2} [P_{n}]) = ⌈ \frac{n}{2} ⌉ + 1 = ⌈ \frac{Δ (P_{2} [P_{n}])}{2} ⌉$ 。

当 $n \equiv 0 (\mod 2)$ 时，上式等价于 $\frac{n}{2} + 1 \leq l a (P_{2} [P_{n}]) \leq \frac{n}{2} + 2$ 。下证 $l a (P_{2} [P_{n}]) = \frac{n}{2} + 2$ 。

假设 $l a (P_{2} [P_{n}]) = \frac{n}{2} + 1$ ，考虑 $P_{2} [P_{n}]$ 中所有顶点的度，易得 $d (u_{i}, v_{j}) = n + 1$ ( $i = 1, 2; j = 1, n$ )，其余顶点的度为 $n + 2$ 。由 $n + 2 = 2 (\frac{n}{2} + 1)$ 知，除四个顶点外，其余顶点在每个线性森林中的度都为2，即这些顶点在每个线性森林路的内部顶点处，此时每条路的两个端点必须在上述四个点上。由于 $n + 1 = \underset{\frac{n}{2} 个}{\underset{︸}{2 + 2 + \dots + 2}} + 1$ ，这四个顶点作为路的端点的次数是1，从而 $P_{2} [P_{n}]$ 的线性森林分解中只有两条生成路，即 $l a (P_{2} [P_{n}]) \leq 2$ 。由于 $n \geq 4$ ，有 $l a (P_{2} [P_{n}]) = \frac{n}{2} + 1 > 2$ ，矛盾。

故 $l a (P_{2} [P_{n}]) = \frac{n}{2} + 2 = ⌈ \frac{Δ (P_{2} [P_{n}]) + 1}{2} ⌉$ 。

情况三. $Δ (T_{m}) \geq 2$ ， $n = 2$ 。

由 $T_{m} [P_{2}] = (T_{m} □ P_{2}) \cup (T_{m} \times K_{2}) = (T_{m} □ P_{2}) \cup (T_{m} \times P_{2}) = T_{m} ⊠ P_{2}$ 及定理1得， $l a (T_{m} [P_{2}]) = ⌈ \frac{Δ (T_{m} [P_{2}])}{2} ⌉$ 。

情况四. $Δ (T_{m}) \geq 2$ ， $n > 2$ 。

由 $Δ (P_{n}) = 2$ 得，

$l a (T_{m} [P_{n}]) \geq ⌈ \frac{Δ (T_{m}) n + 2}{2} ⌉ = {\begin{array}{l} \frac{Δ (T_{m}) n}{2} + 1, & Δ (T_{m}) \equiv 0 (\mod 2); \\ \frac{Δ (T_{m}) n + 1}{2} + 1, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2); \\ \frac{Δ (T_{m}) n}{2} + 1, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2) . \end{array}$

由 $T_{m} [P_{n}] = (T_{m} □ P_{n}) \cup (T_{m} \times K_{n})$ 其中 $V (K_{n}) = V (P_{n}) = {v_{1}, v_{2}, \dots, v_{n}}$ ，有

$l a (T_{m} [P_{n}]) \leq l a (T_{m} □ P_{n}) + l a (T_{m} \times K_{n}) = {\begin{array}{l} \frac{Δ (T_{m}) n}{2} + 1, & Δ (T_{m}) \equiv 0 (\mod 2); \\ \frac{Δ (T_{m}) n + 1}{2} + 1, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2); \\ \frac{Δ (T_{m}) n}{2} + 2, & Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2) . \end{array}$

因此 $Δ (T_{m}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2)$ 时， $⌈ \frac{Δ (T_{m} [P_{n}])}{2} ⌉ \leq l a (T_{m} [P_{n}]) \leq ⌈ \frac{Δ (T_{m} [P_{n}]) + 1}{2} ⌉$ 。□

2.3. 路与树字典积的线性荫度

定理4. $m = 2$ ， $Δ (T_{n}) = 2$ ， $n > 2$ ， $n \equiv 0 (\mod 2)$ 时， $l a (P_{m} [T_{n}]) = ⌈ \frac{Δ (P_{m} [T_{n}]) + 1}{2} ⌉$ ；

$m = 2$ ， $Δ (T_{n}) > 2$ ， $n > 2$ ， $Δ (T_{n}) \equiv 1 (\mod 2)$ ， $n \equiv 1 (\mod 2)$ 或 $m = 2$ ， $Δ (T_{n}) > 2$ ， $n > 2$ ， $Δ (T_{n}) \equiv 0 (\mod 2)$ ， $n \equiv 0 (\mod 2)$ 时， $⌈ \frac{Δ (P_{m} [T_{n}])}{2} ⌉ \leq l a (P_{m} [T_{n}]) \leq ⌈ \frac{Δ (P_{m} [T_{n}]) + 1}{2} ⌉$ ；

其它条件时， $l a (P_{m} [T_{n}]) = ⌈ \frac{Δ (P_{m} [T_{n}])}{2} ⌉$ 。

证明. 设 $P_{m} = u_{1} u_{2} \dots u_{m}$ ， $V (T_{n}) = {v_{1}, v_{2}, \dots, v_{n}}$ 。由定义4得

$Δ (P_{m} [T_{n}]) = Δ (P_{m}) n + Δ (T_{n})$ .

以下分两种情况：

情况一. $m > 2$ 。

当 $Δ (T_{n}) = 1$ 即 $n = 2$ 时，可设 $T_{2} = P_{2}$ ，由定理3情况三有， $l a (P_{m} [P_{2}]) = ⌈ \frac{Δ (P_{m} [P_{2}])}{2} ⌉$ 。

当 $Δ (T_{n}) \geq 2$ 即 $n > 2$ 时， $Δ (P_{m} [T_{n}]) = 2 n + Δ (T_{n})$ ，则 $l a (P_{m} [T_{n}]) \geq n + ⌈ \frac{Δ (T_{n})}{2} ⌉$ 。因为

$P_{m} [T_{n}] = (P_{m} □ T_{n}) \cup (P_{m} \times K_{n})$

其中 $V (K_{n}) = V (T_{n}) = {v_{1}, v_{2}, \dots, v_{n}}$ ，有

$l a (P_{m} [T_{n}]) \leq l a (P_{m} □ T_{n}) + l a (P_{m} \times K_{n}) = n + ⌈ \frac{Δ (T_{n})}{2} ⌉$ .

从而 $l a (P_{m} [T_{n}]) = ⌈ \frac{Δ (P_{m} [T_{n}])}{2} ⌉$ 。

情况二. $m = 2$ 。

此时设 $P_{2} = u_{1} u_{2}$ 。当 $Δ (T_{n}) = 1$ 即 $n = 2$ 时，由定理3得， $l a (P_{2} [T_{2}]) = ⌈ \frac{Δ (P_{2} [T_{2}])}{2} ⌉$ 。

当 $Δ (T_{n}) = 2$ 即 $n > 2$ 时，由定理3得， $l a (P_{2} [T_{n}]) = {\begin{array}{l} ⌈ \frac{Δ (P_{2} [T_{n}])}{2} ⌉, & n \equiv 1 (\mod 2); \\ ⌈ \frac{Δ (P_{2} [T_{n}]) + 1}{2} ⌉, & n \equiv 0 (\mod 2) . \end{array}$

当 $Δ (T_{n}) > 2$ 即 $n > 2$ 时， $Δ (P_{2} [T_{n}]) = n + Δ (T_{n})$ ，从而

$l a (P_{2} [T_{n}]) \geq ⌈ \frac{n + Δ (T_{n})}{2} ⌉ = {\begin{array}{l} \frac{n + Δ (T_{n})}{2}, & Δ (T_{n}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2); \\ \frac{n + Δ (T_{n}) + 1}{2}, & Δ (T_{n}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2); \\ \frac{n + Δ (T_{n}) + 1}{2}, & Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 1 (\mod 2); \\ \frac{n + Δ (T_{n})}{2}, & Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 0 (\mod 2) . \end{array}$

因为 $P_{2} [T_{n}] = (P_{2} □ T_{n}) \cup (P_{2} \times K_{n})$ 其中 $V (K_{n}) = V (T_{n}) = {v_{1}, v_{2}, \dots, v_{n}}$ ，由引理3及定理2有

$l a (P_{2} [T_{n}]) \leq l a (P_{2} □ T_{n}) + l a (P_{2} \times K_{n}) = {\begin{matrix} \begin{matrix} \frac{n + Δ (T_{n}) + 2}{2}, & Δ (T_{n}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2); \end{matrix} \\ \begin{matrix} \frac{n + Δ (T_{n}) + 1}{2}, & Δ (T_{n}) \equiv 1 (\mod 2), n \equiv 0 (\mod 2) \end{matrix}; \\ \begin{matrix} \frac{n + Δ (T_{n}) + 3}{2}, & Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 1 (\mod 2) \end{matrix}; \\ \begin{matrix} \frac{n + Δ (T_{n}) + 2}{2}, & Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 0 (\mod 2) \end{matrix} . \end{matrix}$

$Δ (T_{n}) \equiv 1 (\mod 2), n \equiv 1 (\mod 2)$ 时， $⌈ \frac{Δ (P_{2} [T_{n}])}{2} ⌉ \leq l a (P_{2} [T_{n}]) \leq ⌈ \frac{Δ (P_{2} [T_{n}]) + 1}{2} ⌉$ 。

$Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 1 (\mod 2)$ 时，由 $P_{2} [T_{n}] = T_{n} \cup K_{n, n}$ 及引理1和2有， $l a (P_{2} [T_{n}]) \leq \frac{n + Δ (T_{n}) + 1}{2}$ ，即 $l a (P_{2} [T_{n}]) = ⌈ \frac{Δ (P_{2} [T_{n}])}{2} ⌉$ 。

$Δ (T_{n}) \equiv 0 (\mod 2), n \equiv 0 (\mod 2)$ 时， $⌈ \frac{Δ (P_{2} [T_{n}])}{2} ⌉ \leq l a (P_{2} [T_{n}]) \leq ⌈ \frac{Δ (P_{2} [T_{n}]) + 1}{2} ⌉$ 。□

3. 总结

本文研究了树和完全图直积图，树和路，路和树字典积图的线性荫度，主要利用笛卡尔积图、直积图和字典积图的性质，给出对应乘积图边集的划分，进而确定以上乘积图线性荫度。线性荫度猜想是图论中广泛关注的热点问题之一，至今该猜想还未被完全证明，本文丰富了此领域乘积图的研究成果。目前乘积图线性荫度研究中笛卡尔积图相关结论较多，如完全图分别与路、圈、完全图等特殊图笛卡尔积线性荫度已确定，可在其它三种常见乘积图中继续拓展此研究，笛卡尔积中也有一些特殊图未被研究，例如完全二部图与圈的笛卡尔积图线性荫度的计算等。

基金项目

新疆少数民族科技人才特殊培养计划科研项目(2022D03002)；国家自然科学基金地区科学基金项目(11961070)。

NOTES

^*通讯作者。

参考文献

[1]	Harary, F. (1970) Covering and Packing in Graphs, I. Annals of the New York Academy of Sciences, 175, 198-205. https://doi.org/10.1111/j.1749-6632.1970.tb56470.x
[2]	Akiyama, J., Exoo, G. and Harary, F. (1980) Covering and Packing in Graphs III: Cyclic and Acyclic Invariants. Mathematica Slovaca, 30, 405-417.
[3]	Akiyama, J., Exoo, G. and Harary, F. (1981) Covering and Packing in Graphs IV: Linear Arboricity. Networks, 11, 69-72. https://doi.org/10.1002/net.3230110108
[4]	Enomoto, H. and Péroche, B. (1984) The Linear Arboricity of Some Regular Graphs. Journal of Graph Theory, 8, 309-324. https://doi.org/10.1002/jgt.3190080211
[5]	Guldan, F. (1986) The Linear Arboricity of 10-Regular Graphs. Mathematica Slovaca, 36, 225-228.
[6]	Wu, J.-L. (1999) On the Linear Arboricity of Planar Graphs. Journal of Graph Theory, 31, 129-134. https://doi.org/10.1002/(SICI)1097-0118(199906)31:2%3C129::AID-JGT5%3E3.0.CO;2-A
[7]	Wu, J.-L. and Wu, Y.-W. (2008) The Linear Arboricity of Planar Graphs of Maximum Degree Seven Is Four. Journal of Graph The-ory, 58, 210-220. https://doi.org/10.1002/jgt.20305
[8]	李萍. 树和路乘积图的线性荫度[J]. 应用数学进展, 2022, 11(3): 1242-1246. https://doi.org/10.12677/AAM.2022.113134

为你推荐

友情链接