基于Markov状态转换的高频统计套利策略研究

Research on High-Frequency Statistical Arbitrage Strategy Based on Markov State Transition

摘要: 做空与对冲机制的放开使得配对交易策略可行，协整配对的套利策略被有效促进和发展。本文引进Markov状态转换模型构建交易策略，它能够较好地解释市场状态变动的过程，并结合OU过程求得满足期望收益最大条件下的最优入场交易信号。研究表明，Markov模型将市场分为“高波动”和“低波动”两种状态，高波动的存在客观上影响了配对交易的收益。同等风险下，基于马尔可夫状态转换模型策略的配对交易收益要比基于协整模型的收益情况更优，收益率的波动更稳定风险更小。

Abstract: The pairing trading technique is practicable thanks to the liberalization of the short and hedge mechanisms, and co-integration pairing trading is effectively promoted and developed. In order to build a trading strategy, a Markov switch model is introduced in this study. This model can provide a better explanation of the process of market state change, and combined with the OU process obtain optimal entry trading signals that satisfy the greatest expected return. In conclusion: the market is divided into two states by the Markov model: "high volatility" and "low volatility", and the presence of high volatility objectively affects pair trading returns. The returns of pairing trading using Markov switch model are better than those using a co-integration model at the same risk; volatility of yield is more stable and less risky.

1. 引言

上世纪八十年代，统计套利方法在金融领域中风行一时，在跌宕起伏的市场中基金公司和量化团队赚取了可观的收益。长期以往，统计套利在市场中被广泛应用，基于历史数据进行客观分析，建立投资模型，不仅消除了部分错误的非理性的定价，还有效提高了市场流动性，放大了资金的使用效力，对市场、研究者和投资者都具有积极的投资指导意义。

在国外，专业投资研究者开始在市场中对配对交易进行了大量的多角度的研究应用和创新。Schaller等在研究美国股票市场时，考虑股市中波动率存在状态变化的情况，发现状态转换在股票市场中表现显著，另外价差序列当中也存在状态转换行为 [1]，市场收益波动率与期望收益在不同状态下有明显差异。Klaassen [2] 将马尔可夫模型与GARCH模型结合研究的同时对模型进行了优化和改进，采用极大似然法进行估计，更好描述不同状态转换间时间序列数据突变结构的波动；采用更广泛的信息集计算，使得预测精度更加准确。Walid C等基于新兴国家市场，研究股票价格波动与汇率变化之间的动态关系时，构建马尔可夫转换-EGARCH模型，结果区分出两种不同的制度 [3]。之后Yang等对标普500成份股6年数据构建模型 [4]，对不同行业比较策略表现，研究表明，基于状态转换与无状态转换的交易策略相比，状态转换策略在金融行业获得的收益效果更好。

国内学者近几年在配对交易的研究上也做出了许多贡献，如朱钧钧 [5] 利用Markov转换及自回归模型对上证综指周收益率、波动率进行建模，收益率在不同状态之间的变动有明显差异，股市波动状态呈现持续时间较短。魏巍贤、胡志强等 [6] [7] 在市场和行业的研究中，均区别出了三状态转换模型，同时发现Markov状态转换模型常用来对宏观经济以及市场波动动态非线性模型的研究。刘健 [8] 在研究资产投资组合的过程中，使用Markov模型提前捕捉到了市场状态转换的过程，且验证了状态变化有效增加投资组合的价值。

基于价差序列的均值回复特征，Bertram [9] 求得了当OU过程可以更好地拟合具有明显均值回复特征的价差序列时，满足期望收益值和夏普比率最大化这两个限定条件下对应的最优交易信号，并确立了收益率最大化对应的最优套利区间。黄晓薇等 [10] 首先将随机控制理论引入到股票配对交易中，证实利用OU过程的最优配对套利策略相比传统的协整模型收益率更高、交易成本也低，可显著提高现代金融市场的运行效率。

在配对交易投资研究中，以往学者擅长运用传统策略进行配对交易，且容易忽略高频交易能抓取更多套利机会的优势，相同策略下频数越高越容易获取高收益率 [11]，然而交易频率也不能过高，若频率低于30分钟反而容易失去大量套利机会。本文将从实际角度出发，重点将Markov状态转换应用到配对量化投资交易，它能够较好地解释市场状态转换的过程及刻画在变动的状态下收益率的明显差异。

2. 套利模型与交易信号

2.1. Markov状态转换模型

近几年国内外非线性模型的理论愈发成熟，Markov状态转换模型是一种动态时间序列模型，相较于其他一般线性模型而言，能够很好的描述宏观经济和金融市场序列在不同状态下的转换波动情况。马尔可夫链是一种特殊的随机过程，设随机过程 $\left\{s_t:t=0,1,\cdots ,T\right\}$ 是一个取值为离散状态空间 $S=\left\{1,2,\cdots ,n\right\}$ 的马尔可夫链 [12]，则有

1) $P\left\{s_t=j|s_{t-1}=i,s_{t-2}=k_2,\cdots \right\}=P\left\{s_t=j|s_{t-1}=i\right\}=p_{ij}$，其中 $p_{ij}$ 为一步转移概率，即表示从处于状态i的过程转移到下一个状态j的概率。这说明未来 $t+1$ 时刻的状态只与前一个t状态有关，与过去t时刻之前的状态无关，这个过程称为N状态马尔可夫链。

2) 对于马尔可夫状态转移模型，我们知道转移是随机的，因此无法确定是否会有状态转移，因此将转移概率列成转移概率矩阵 $P=\left(p_{ij}\right)$，可以清晰地看出转移过程。 $p_{ij}$ 具备以下性质： $p_{ij}\ge 0$， ${\displaystyle {\sum }_{i,j}{p}_{ij}}=1$， $\forall i,j\in R$。这两条性质印证了概率的非负性和状态转移的一致性。得出两状态转移概率矩阵为 $P=\left(\begin{array}{cc}p& 1-p\\ 1-q& q\end{array}\right)$，其中p表示当前t与 $t+1$ 时刻均处于1状态的概率，q表示当前t时刻处于2状态， $t+1$ 时刻也处于2状态的概率。记 $X_t$ 为已知时间序列，平滑概率 $P\left(S_t=n|x_1,\cdots ,x_T\right)$ 表示用所有时刻的已知信息，衡量t时刻 $S_t=n$ 的概率。当 $t<T$ 时，可判断t时刻处于某一状态的概率。

然而常见的多元状态转换模型存在参数推断的困难，为简化模型，假定价差序列仅存在两状态：高波动和低波动。对Markov模型参数的估计使用极大似然估计法，假设关于参数 $\theta$ 的条件对数似然函数为： $L\left(\theta |X_{t-1},X_{t-2},\cdots ,X_1\right)$，具体使用卡尔曼滤波过程计算似然函数。假设序列服从一个OU过程，即： $\text{d}{X}_t=\lambda \left({\mu }_i-X_t\right)\text{d}t+{\sigma }_i\text{d}{b}_t$， $S_t=k_i$， $i=1,2$，其中 $S_t$ 表示样本对应的状态，转换参数可以写成： $X_{t+\Delta t}={\alpha }_{st}+{\beta }_{st}{x}_t+{\epsilon }_t$，因此模型构造的参数为 $p,q,\alpha ,\beta ,\sigma$。

2.2. 构建交易信号

套利策略试图获取资产组合的价差，利用均值回归属性来盈利，按照一定标准构建交易信号。当价差波动偏离均值，且触发开仓信号，卖出被高估的资产，买入被低估的资产；当价差序列靠拢，直到回复均值附近，进行反向操作，根据设计的模型做出多头和空头头寸策略。

假设当 $x_t=a$ 时发出建仓信号，当 $x_t=b$ 时发出平仓信号；待下次 $x_t=a$ 时再次发出建仓信号，依次反复。由此其中一个套利过程可看作残差序列 $x_t$ 由a至b的过程，我们将该过程又称作交易周期t，t是一个随机变量。进一步假设 $a<b$，假设成功交易一次暂时不计交易费用，则此次交易获得的收益表示成： $b-a$。根据交易情况可以分为 $t_1$ 和 $t_2$，分别代表持仓时间和空仓时间。因为 $x_t$ 是一个马氏过程，故持仓空仓相互独立。再假设某个周期内交易成本为c，则收益 $r\left(a,b,c\right)=b-a-c$。根据伊藤定理对去中心化价差序列 $x_t$ 进行变量替换，得到 $Y_t=x_t\sqrt{2\lambda }/\sigma$， $\tau =\lambda t$，故可求出交易周期的均值为 $E\left(t\right)$。为了使期望收益最大化，对期望函数 $E\left(t\right)$ 分别对 $a,b$ 求偏导，得到 $b=-a$，且根据泰勒公式、盛金公式计算可得到套利交易最佳进入点a， $\Delta$ 也已知。

3. 实证分析

3.1. 研究标的与检验

选取的沪深300成分股中华泰证券(601688.XSHG)和同花顺(300033.XSHE)两只股票2022-05-01 09:30:00至2022-10-01 15:00:00的60分钟高频数据作为此次交易策略的数据，两者相关系数为0.85，初步推断两者可能存在协整关系。

数据分析以及参数估计、样本实证通过Python、R实现。下图为缩量处理后(同花顺股票缩小十倍)两只股票的收盘价走势图，见图1，两只股票收盘价趋势相关性较强，存在较大套利空间，可根据理论分析及策略模型进行股票对统计套利的实证研究。

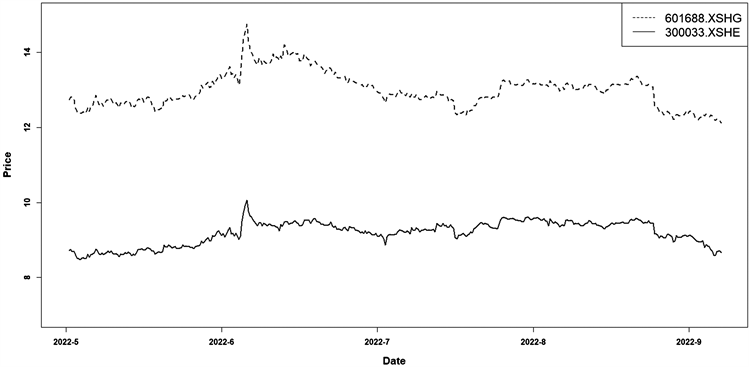
Figure 1. Comparison of stock close prices

图1. 股票收盘价对比

为进一步证明两只股票间是否存在长期均衡相关关系，进行ADF检验。如表1所示，华泰证券和同花顺0阶单整检验T检验的p值均大于0.05，在置信水平为1%、5%和10%的情况下，都拒绝原假设：序列有单位根，两者都是非平稳的；进而观察1阶单整检验，T检验p值小于0.05，具有平稳性，可以确定序列是1阶单整的。

Table 1. ADF test for stocks

表1. 股票ADF检验

在计量经济学和数理金融领域，没有因果关系的经济变量进行回归容易出现伪回归情况。于是经济学家提出格兰杰因果检验试图寻找区别变量之间因果关系的方法。Granger因果检验的实质是依赖于用过去所有时刻的信息去预测最优最小二乘的方差。

Table 2. Granger causality test

表2. Granger因果检验

由上表2得，所有X、Y的滞后期中，回归分析结果具有显著性，p值都小于0.05，拒绝原假设，认为同花顺是引起华泰证券变化的原因，将华泰证券收盘价作随机变量Y，同花顺作随机变量X。

3.2. 基于协整的配对交易

随着我国金融市场的统计套利策略被有效促进和发展，市场风险的存在加剧了国内股票市场的波动，而高频数据包含的信息更多，能更加及时地反映出市场的波动现象。因此观察到高频价差序列满足均值回复特性，股票价差序列均值 $\mu$ 为0.1983，方差为0.0145，去中心化价差序列为 $msprea{d}_t=sprea{d}_t-\mu$，交易信号序列为 $zsprea{d}_t=msprea{d}_t/RMSD$。

协整检验是检验两个时间序列组成的配对资产线性关系是否是协整的，即残差序列是否满足平稳性的条件。通过最小二乘法计算得出，R²和调整R²都为0.83，说明拟合情况较好，F检验统计量为1914，p值为0，通过检验。

Table 3. Logarithmic close price OLS regression

表3. 对数收盘价OLS回归

由表3，回归模型为 $InY=0.1983+0.5310\ast InX+{\epsilon }_t$，继续检查该残差序列的平稳性，残差方程为 ${\epsilon }_t=InY-In\hat{Y}$。见表4，残差序列 ${\epsilon }_t$ 的ADF检验的p值为1.17e−29，因此残差序列平稳的，不存在单位根，这表明华泰证券和同花顺股票价格之间存在长期均衡的关系。

Table 4. ADF test for residual sequences

表4. 残差序列ADF检验

该价差序列 $sprea{d}_t=InY-0.531\ast InX$ 表明华泰证券和同花顺之间的均衡价差水平，这里的系数可以用来构建股票对的做多与做空组合，即每做多(做空) 1份同花顺股票就要做空(做多) 0.531份华泰证券，就可以满足交易组合市场中性的条件。

为了尽可能模拟真实交易，假设初始资金为100,000元，每次交易为全仓交易，考虑到实际上有做空部分为融券，固有杠杆的效果，交易费用为2‰。传统协整策略是以价差的固定标准差作为触发交易的阈值，建仓交易信号设为0.6倍标准差，回归、穿越均值进行平仓，止损(平仓)信号为2倍标准差。配对交易具有一定的强制平仓风险，所以将交易总仓位控制在50%左右。

首先对样本交易结果进行分析，华泰证券和同花顺在2022-05-01 09:30:00至 2022-10-01 15:00:00共发生10次交易。其中正收益次数为8次，负收益次数为2次，交易成功率为80%，样本的累积净收益率为15.22%。交易间隔为60分钟，套利收益情况、信号图2~图4如下：

Figure 2. Diagram of the returns

图2. 收益图

Figure 3. Diagram of the risk

图3. 风险指标图

样本数据选取的是2022年5月至9月的全部股票数据，其中包含重大节日等时刻，实际上，由图2发现样本内的负收益大都发生在5~6月期间，这导致交易成功率降低及累积收益率减小，从图3风险及收益指标可直观地看出，价差序列的剧烈波动情况与6~7月收益情况变化以及股票最大回撤的大幅度跳跃变化相吻合。具体套利情况如下图4所示：

Figure 4. Arbitrage of cointegration model

图4. 协整模型套利

3.3. 状态转换配对交易

从配对股票价差序列的构建过程以及描绘出的价差序列的结构性变化形态可看出，价差序列在一定时期内并非是简单的非线性形式，股票收盘价的无规律波动变化存在状态来回转换的可能 [13]，在具备两状态转换的情况下进行配对交易的收益是否比传统的策略收益更好呢，因此试图引入Markov模型重新搭建配对交易模型。

偏离均值的波动程度会随着时间的推移发生变化，因此按照市场特性可分为“高波动”和“低波动”两种不同的状态，不同的状态下对应承担的市场风险以及产生收益情况也不同，因此把市场状态的转换考虑到对资产配对交易的影响中，可以针对不同的状态设置不同的参数，建立不同的最优投资策略，这更利于帮助投资者辨别市场状态转变的过程合理进行股票配对交易。因此，采用马尔可夫状态转换的思想进行套利交易，用MS-AR (4)模型检验模型参数，因模型只用到1阶预测，故仅保留1阶参数，其划分结果见表5：

Table 5. MS model parameter estimation results

表5. 状态转换模型参数估计结果

状态1、2的均值分别为−0.029和−0.0215，对数方差 ${\sigma }_2$ 分别为8.6e−06和3.09e−05，且Z统计量值和P值显示各个系数都是显著的，状态1对数方差 ${\sigma }_2$ 较小些，因此可把状态1看作“低波动”状态，状态2看作“高波动”状态。

Table 6. Transform probability matrix

表6. 转移概率矩阵

从表6 转移概率矩阵得，p₁₁表明状态1保持状态不变的概率为0.9702，p₁₂为0.0298，说明低波动跳跃到高波动状态的概率为0.0298，同理状态2转向状态1的概率为0.1231，存在高、低波动的状态转换。对比协整策略收益图和高低波动平滑概率图，负收益交易大多数发生在价差序列位于状态2的时候，故认为状态2高波动的存在的确在客观上影响了统计套利的收益。p₁₁和p₁₂的概率都大于0.85，说明不管在哪种状态， $t+1$ 时刻都会以大于0.85的概率保持状态不变，任何时刻都只能属于一个状态——状态1或者状态2，因此设定在状态1的平滑概率大于0.8时，则判别为“低波动”，处于状态2的平滑概率大于0.8时，为“高波动”状态。如下图5为价差序列的“低波动”与“高波动”概率图：

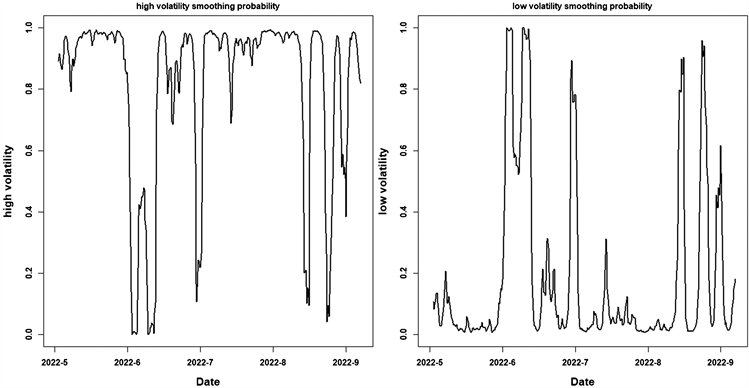
Figure 5. Smoothing probability plot of high volatility and low volatility of spread series

图5. 价差序列高波动、低波动平滑概率图

求出华泰证券和同花顺在Markov模型下对应的部分随机参数， $\lambda =-\ln \left(\beta \right)/\Delta t$， $\theta =\alpha /\left(1-\beta \right)$， $\sigma =2\ast \lambda \ast \mathrm{var}/\left(1-{\beta }^2\right)$，见表7。

Table 7. Estimate the model parameters

表7. 估计模型参数

时间间隔取 $\Delta t=1/252$，设定回归、穿越均值进行平仓，止损(平仓)信号为2倍标准差。“低波动”状态下，交易信号阈值 $a_1=-0.0038$，“高波动”状态下，阈值较高， $a_2=-0.0070$， $st{d}_{spread}=0.0145$，其他时刻建仓交易信号设为0.6倍标准差，最优建仓交易阈值 ${\Delta }_1=-2\ast a_1/std=0.5195$， ${\Delta }_2=-2\ast a_2/std=0.9709$。说明状态1和状态2的建仓是存在差异的，根据最优交易阈值在每个时刻确定动态套利策略，考虑状态转换来构建配对交易策略是比较恰当的。下图6为马尔可夫状态转换套利情况：

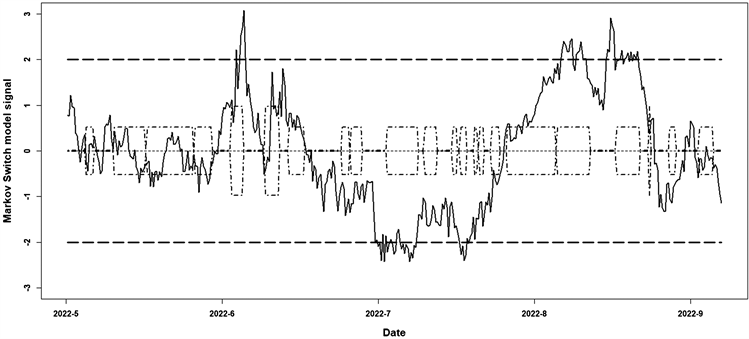
Figure 6. The returns of pairing trading using Markov switch model

图6. 基于Markov状态转换模型套利情况

从图6看出，华泰证券与同花顺在2022-05-01 09:30:00至 2022-10-01 15:00:00共发生13次交易。交易次数比协整模型策略有所增加，交易包括11次正收益，2次负收益，交易成功率为84.6%，交易成功率提高。针对收益度量，采用累计收益率和平均收益率。针对风险度量，采用夏普比率和最大回撤。下表8为两种策略下评估指标的对比情况：

Table 8. Comparison of returns under the two strategies

表8. 两种策略下的收益情况对比

结果显示，夏普比率越高，说明单位风险下能够获得更多的超额收益；最大回撤越小说明模型稳健性越高，构建的模型配对策略也越好。协整套利策略的夏普比率为3.01，马尔可夫状态转换模型策略的夏普比率值为3.43，两者对比体现协整套利在参数设置问题上还存在一定的局限性，后者的策略在承受同等风险的条件下，可以多获取0.42单位的收益。策略的最大回撤分别为24.39%和22.17%，说明马尔可夫模型构建的更稳健，交易成功率更高。

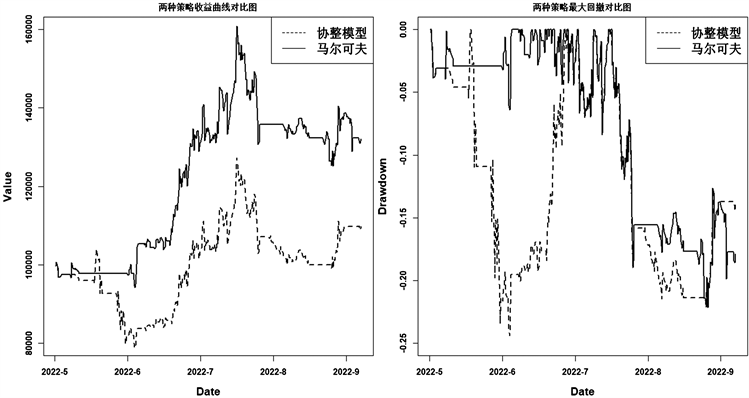
Figure 7. Comparison of the maximum drawdown and yield curve of the two strategies

图7. 两种策略最大回撤对比及收益曲线

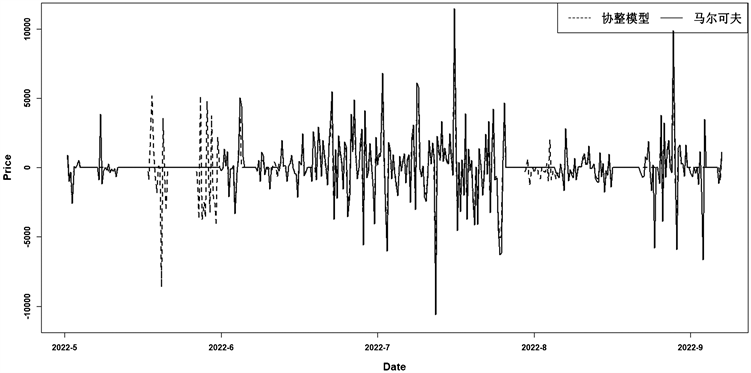
Figure 8. Comparison of yield volatility of the two strategies

图8. 两种策略收益率波动对比

为了更直观的观察和对比两种策略的效果，最后结合最大回撤图以及收益曲线图进行观察：尽管Markov模型风险也存在，但交易后期最大回撤明显降低，结合图7观察到对应时期也有很大机会获取超额利润。套利过程中股票收益的波动更稳定，策略更好。反之也证实了要减小投资风险，降低最大回撤可作为一种有效方法。

虽然考虑状态转换情况发生交易的次数与前者相比没有明显增多，但在最大回撤可控的情况下，很容易从图7对比图看出Markov模型策略优于传统策略，说明马尔可夫状态转换策略更能准确捕捉交易信号，收益率、净利润比协整模型更高，恰恰体现出基于状态转换模型策略的严谨性与可靠性，由图8，Markov收益率波动情况要比协整模型剧烈，因此更能反映出市场状态的变动，两种情况的对比也便于投资者根据自身风险承受度作出较为合理的决策。

4. 结束语

统计套利策略作为一种中性策略，可以更好地规避市场非系统性风险，因此本文重点分析了基于Markov状态转换模型的对金融时间序列高频数据进行统计套利的研究。分析显示，在样本期间高频数据更能从价格反映出信息的灵敏程度，结合协整模型构建单一模态的套利交易形式，发现可以获得收益，出现负收益的情况可能是其他原因的存在影响了套利，比如市场状态的波动导致股票价差存在时变方差性等。为进一步研究金融时间序列存在结构变化波动的特征，并且结合Markov状态转换模型构建统计套利策略，最后检验和比较两种策略在实践中的套利绩效和对市场效率的影响。结果发现，基于Markov状态转换模型的套利策略能反映出市场的变动，能灵敏地抓取各个波动状态反映的信息，发现其内在变化机制，获得更可观的回报，从而会更好地规避市场风险，捕捉交易机会，提高市场投资效益。

基金项目

国家自然科学基金项目“几类非线性随机切换系统的控制及其稳定性分析”(62003170)

江苏省自然科学基金项目“非线性随机时滞系统的控制器设计及稳定性分析”(BK20190770)。

参考文献