机场出租车载客优化问题研究

Research on Optimization of Airport Taxi Carrying Passengers

摘要: 针对机场出租车司机等待载客、放空返回的选择问题，研究了一种提高出租车司机运载乘客效率与收益的选择策略。根据模型的合理性和相关因素的依赖性，建立了基于多属性的出租车司机接客决策树模型，并通过Python的爬虫技术获得交通信息数据集，在基于大数据的程序批量预处理后，协同其他不确定属性验证模型的可行性。建立了数学模型，试验测试计算结果表明：当计算得平均到达率λ = 5.98、单个上车点的平均服务率μ = 2.21、乘客等待的时间费用w = 0.001时，模型可靠性最高，且上车点数量m等于5时乘客时间成本、出租车时间成本与效益值达到最优，实现排队服务系统成本和费用最小。

Abstract: Aiming at the choice problem of airport taxi drivers waiting for passengers and returning empty, a selection strategy to improve the efficiency and income of taxi drivers to carry passengers is stud-ied. According to the rationality of the model and the dependence of related factors, a multi-attri- bute-based taxi driver pick-up decision tree model is established, and a traffic information dataset is obtained through Python crawler technology. After batch preprocessing of programs based on big data, the feasibility of other uncertain attribute verification models is coordinated. A mathematical model is established, and the experimental test calculation results show that when the calculated average arrival rate λ = 5.98, the average service rate μ = 2.21 of a single boarding point, and the passenger waiting time cost w = 0.001, the reliability of the model is the highest, and when the number of boarding points m is equal to 5, the passenger time cost, taxi time cost and benefit values are optimal, and the cost and cost of the queuing service system are minimized.

1. 引言

近年来，随着世界经济的飞速发展，人民生活水平不断提高，旅游业也得到了前所未有的发展，所以无论是从频率还是从出行方式上，人们的选择意识都发生了很大转变，飞机已经逐渐成为人们长途旅行的主流选择。由于机场大多是修建在远离市区的地方，位置相对比较偏，很多乘客下飞机后要去市区或周边的目的地，出租车是机场出行的主要交通工具。

出租车作为乘客出行方式的重要一环 [1]，在其中充当着重要作用，并且多年来形成的传统的运输营业模式已经无法满足旅客、司机等各方面的需求 [2]。如何进行调配以平衡出租车与乘客之间的供需关系 [3]；以及怎么抉择，保证司机利益最大化的同时 [4]，尽可能满足乘客需求，在供应乘客运输的条件下 [5]，最大程度提高出租车运输效率是摆在机场管理方面的一道难题 [6]，受到许多学者们的关注 [7]。更进一步的，搭载乘客的人数和行驶里程与出租车司机的收益都是有相关性的 [8]，短途载客的司机与长途载客的司机、满载乘客的司机与载乘客较少的司机相比较而言，利益差距过大。为了平衡出租车司机的收益，管理部门欲给一部分短途载客并且继续返回机场拉客的出租车一定的“优先权”，而给长途载客并且需要稍等待乘客满载的司机一定的“滞留”时间，从而需要给出一个可以在现实中实行的优先安排方案。针对乘客与出租车供求关系不平衡所导致的乘车效率低下的问题，我们将问题模型化，通过建立合适的上车点、乘车时间段，对出租车与乘客合理调度，使得总的乘车效率提高。首先是对已有的相关研究进行回顾，其次针对不同的问题建立最优化模型，之后讨论所建模型中待求参数的估计方法与结果，最后对模型的求解结果进行检验并总结。

2. 机场出租车问题研究

2.1. 决策树模型

对于出租车司机选择空载返回还是选择等待载客的决策问题，本文选择用决策树模型进行求解。

定义熵的概率分布为 $P\left(X=x_i\right)=p_i,i=1,2,\cdots ,n$，那么将出租车司机决策模型中特征A给定条件D的经验条件熵 $H\left(D\right)$ 与特征A给定条件下D的经验条件熵 $H\left(D|A\right)$ 之差记为 $g\left(D|A\right)$，其中 $g\left(D,A\right)=H\left(D\right)-H\left(D|A\right)$。根据决策树模型理论，可以得到如下结论：

1) 数据集D的经验熵：

$H\left(D\right)=-{\displaystyle {\sum }_{k=1}^K\frac{\left|C_k\right|}{\left|D\right|}{\log }_2\frac{\left|C_k\right|}{\left|D\right|}}$ (1)

2) 特征值A对数据集D的经验条件熵：

$H\left(D|A\right)={\displaystyle {\sum }_{i=1}^n\frac{\left|D_i\right|}{\left|D\right|}H\left(D_i\right)}=-{\displaystyle {\sum }_{i=0}^n\frac{\left|D_i\right|}{\left|D\right|}}{\displaystyle {\sum }_{k=1}^K\frac{\left|D_{ik}\right|}{\left|D_i\right|}{\log }_2\frac{\left|D_{ik}\right|}{\left|D_i\right|}}$ (2)

3) 信息增益：

$g\left(D,A\right)=H\left(D\right)-H\left(D,A\right)$ (3)

4) 特征A对训练数据集D的信息增益比：

$g_R\left(D,A\right)=\frac{g\left(D,A\right)}{H\left(D\right)}$ (4)

根据对上述决策树的信息增益分析，绘制出的决策树模型如图1所示，其中Z表示判断结果，Qty表示排队等候收益，Qtn表示空载返回收益，t₁表示排队等候到接到乘客的时间，t₃表示空载返回到接到乘客的时间，Tp表示乘客的疏散时间，Tc表示出租车的疏散时间。

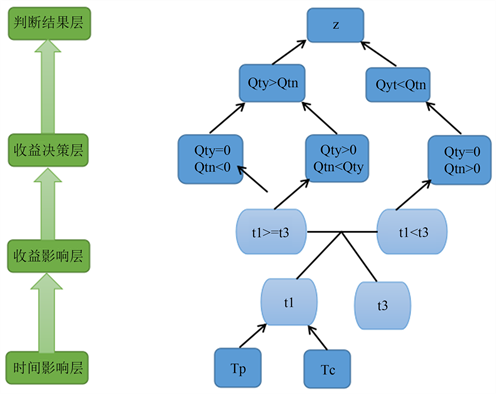
Figure 1. Flowchart of decision tree model

图1. 决策树模型流程图

2.2. Python爬虫

使用实际机场数据对2.1中的决策树模型加以验证，数据收集及预处理的过程如下：

1) 先基于决策树模型的底层影响因素，判断出影响司机决策的主观因素需要用到的验证集，即该时间段航班数据集和最高效空载距离集；

2) 然后通过Python爬虫技术，获得沈阳桃仙机场入港航班的数据集和沈阳出租车GPS定位的打车需求量和出租车分布的特征数据集；

3) 再通过Python进行数据集清洗预处理，得到某一时间段航班数量表和最高效空载距离，通过类比推理的思想，将百度地图热度图数据作为短距离运输最高效空载距离参考；

4) 最后通过Python进行决策树构建以及大数据运算，得出每天每个时间段的出租车司机决策结果。

2.3. 费用决策

若要在供应乘客运输的条件下，最大程度提高出租车运输效率，这需要求解使乘客的等待时间和上车点建设成本最少的上车点个数，使得总的乘车效率最高。很显然，上面所描述的是一个带有约束条件的最优化问题。

本文设计一个预方案以预估结果：假设第一个出租车在第一个上车点接人，从第一个出租车停在第一个上车点的那一时刻开始计时，即此时t = 0，后面来的每一辆车都找到最近的且没有其他出租车停靠的上车点停车接客，将上车点依次编号为①，②，③，④，⑤……，再把按顺序进入乘车区的批量出租车的编号为 $i=1,\cdots ,n$。下面列举了n = 2、4、8时可以设置的上车点的最少数量以及乘客分布，数据如表2、表3、表4所示。其中Ci表示第i量出租车在某时刻，停留在相应编号的上车点。

Table 1. n = 2 the minimum number of pick-up points and the distribution of passengers

表1. n = 2时上车点的最少数量以及乘客分布

Table 2. n = 4 the minimum number of pick-up points and the distribution of passengers

表2. n = 4时上车点的最少数量以及乘客分布

Table 3. n = 8 the minimum number of pick-up points and the distribution of passengers

表3. N = 8时上车点的最少数量以及乘客分布

从表1~3可以得到的结论是：当n = 2时，至少设置两个上车点，每个上车点乘客比例约为1:1；当n = 4时，至少设置三个上车点，每个上车点乘客比例约为2:1:1；当n = 8时，至少设置三个上车点，每个上车点乘客比例约为3:3:2。

下面令λ表示乘客的平均到达率，μ表示单个上点的平均服务率，m表示上车点的个数，η表示系统服务率，w表示乘客等待的时间费用，L_y表示排队服务系统决策成本费用。由于机场外的行车道不会无限长，所以排队系统在稳定工作状态时，系统中出租车乘客数概率如下：

$P_0\left(m\right)={\left[{\displaystyle {\sum }_{i=0}^{m-1}\frac{1}{k!}{\left(\frac{\lambda }{\mu }\right)}^k}+\frac{1}{m!}\frac{1}{\left(1-\eta \right)}{\left(\frac{\lambda }{\mu }\right)}^m\right]}^{-1}$ (5)

$P_n\left(m\right)=\{\begin{array}{l}\frac{1}{n}{\left(\frac{\lambda }{\mu }\right)}^k{P}_0\left(m\right),n=1,2,\cdots ,m\\ \frac{1}{m!m^{n-m}}\left(\frac{\lambda }{\mu }\right)P_0\left(m\right),n=m+1\end{array}$ (6)

对系统进行分析得：

$L_y=L_x+m\eta =\frac{1}{m!}\frac{{\left(m\eta \right)}^m\eta }{{\left(1-\eta \right)}^2}{P}_0+\frac{\lambda }{\mu }$ (7)

$E\left(T\right)=\frac{P_n\left(m\right)}{m\mu {\left(1-\eta \right)}^2}=\frac{n\mu }{n!{\left(n\mu -\lambda \right)}^2}{\left(\frac{\lambda }{\mu }\right)}^n{P}_0\left(m\right)$ (8)

利用排队系统的费用决策模型对排队服务系统进行优化，需要满足两者之和最小才能使排队系统进一步优化，即：

$\min Z\left(m\right)=Z_1+Z_2$ (9)

$Z\left(m\right)\le Z\left(m+1\right)$ (10)

$Z\left(m\right)\le Z\left(m-1\right)$ (11)

其中，约束条件为：

$\omega \left(L_y\left(m\right)-L_y\left(m-1\right)\right)\le \upsilon \le \omega \left(L_y\left(m+1\right)-L_y\left(m\right)\right)$ (12)

根据搭乘出租车的乘客数可计算出对应的乘客的到达率和系统服务率，结果如表4所示。

Table 4. Passenger arrival rate and service rate

表4. 乘客到达率与服务率

接下来使用费用决策模型对沈阳桃仙国际机场的出租车上车点及排队服务系统进行优化，费用决策模型计算结果如表5所示。

Table 5. Calculation results of the cost decision model

表5. 费用决策模型计算结果

由上述计算结果可知，当m = 5时，满足原模型的约束条件，也即此时乘客时间消费和上车点及系统的成本之和最小。这说明了当设置5个出租车上车点时，可实现排队服务系统的成本和费用相对较小。

2.4. 应用

2.4.1. 应用说明

为了平衡出租车司机的收益，需要给出一个“优先安排”方案。这可以概括为需要对之前建立的决策树模型的时间距离收益属性加以改善，提供有针对的补偿措施。

首先将基于GPS定位的打车需求量和出租车分布的特征数据集进行目的地概率预测，得出地点概率预测列表和距离概率期望值；其次求出决策树模型第二层的时间距离收益的拐点，找到即使比排队时早接客但是由于空载原因使收益仍然低于排队的时间或距离区间；再对这个区间进行长途短途分类；最后结合实际情况得出最优方案。

2.4.2. 实例验证

如表6所示，我们将沈阳桃仙机场2021年9月12日出租车进场出场数据作为初始条件，以1小时为时间间隔，计算24个时间段内各自所需的最少上车点。

首先，利用2.3费用决策中的预方案，分别计算n = 2、n = 4、n = 8时上车点的最少数量，如表7所示；根据费用决策模型的约束条件，计算得出乘客平均到达率λ、单个上车点的平均服务率μ、乘客等待的时间费用w分别为5.98、2.12、0.001，与费用决策模型计算结果的相对误差较小；经上述数据及相关计算得到了如表8所示的排队服务系统决策成本费用表，由此可知，当上车点数量m等于5时，乘客时间成本、出租车时间成本与效益值达到最优，实现排队服务系统成本和费用较小。

Table 6. Taoxian airport 2021.9.12 initial data

表6. 桃仙机场2021.9.12初始数据

Table 7. n = 2, n = 4, and n = 8 the minimum number of pick-up points in the expense decision

表7. 费用决策中n = 2、n = 4、n = 8时上车点的最少数量

Table 8. Schedule of decision costs for queuing service systems

表8. 排队服务系统决策成本费用表

3. 模型评估

3.1. 模型的优缺点

1) 模型的优点

a) 决策树模型能够将一系列大数据进行处理，从而得到可靠结果；费用决策模型将抽象问题具象化，使模型更易于理解；

b) 设置多组变量分别对可能产生的多种因素具体讨论，增强模型合理性；

c) 模型比较简单，能够直观地反映出权重的相关影响因素以及权重之间的关系；

d) 模型假设不考虑微观因素的影响，使得模型更易操控，普遍性和适用性更强。

2) 模型的缺点

a) 本文所建立的模型对数据的依赖性很强，必须保证数据本身的准确性；

b) 多点纵列式排队模型对区域的纵向距离要求较高，一般适用于机场交通枢纽，道路较短的不适用；

c) 模型设计中考虑的情况不够完全，假设过于理想化；

d) 模型拓展性不高，容易受外界因素的影响。

3.2. 模型的推广与改进

本文所建立的优化模型除了适用于机场的出租车问题外，还适用于客运站拉客等一系列接客问题。虽然本文提出出租车停靠方案能提高乘客的乘车效率，但是影响乘车效率的因素还有很多，比如天气、时间等，因此还可以将更多因素考虑进去对模型加以改进。