Beta四元数样条曲线相关问题研究

Research on the Beta Quaternion Spline

摘要: 为了更加灵活地调控单位四元数样条曲线，局部控制样条曲线形状，本文基于球面Bézier曲线，将欧氏空间中的Beta样条曲线推广到四元数空间，给出Beta四元数样条曲线定义。证明了该样条曲线满足G¹连续，给出了满足G²连续的充要条件及其证明。最后通过数值实验验证该方法的可行性。本文构造的四元数样条曲线是由控制多边形的顶点直接定义曲线控制顶点，只需改变某段形状参数的取值，即可局部调控样条曲线形状。

Abstract: In order to control the unit quaternion spline more flexibly locally, this paper generalizes the Beta spline in the Euclidean space to the quaternion space based on the spherical Bézier curve, and gives the definition of the Beta quaternion spline. It is proved that the spline satisfies the first-order ge-ometric continuity. The Sufficient requisites for satisfying the second-order geometric continuity and the proof are given. Finally, numerical experiments are used to verify the feasibility of the pro-posed method. The control points of quaternion spline constructed in this paper are directly de-fined by the points of the control polygon, and the spline shape can be controlled locally by simply changing the value of some shape parameters.

1. 引言

单位四元数曲线在机器人控制和计算机动画领域得到了广泛的关注。在计算机动画中，四元数被引入作为一种有用的表示法来插补3D方向 [1]。特别是，单位四元数适用于控制3D对象和虚拟相机的旋转。单位四元数的一个优点是它们没有万向节锁等奇异性。因此，如何设计单位四元数曲线在计算机动画中占有重要地位。

Barsky [2] 将几何连续条件引入B样条曲线，从而构造出来均匀三次Beta样条基函数。Beta样条曲线既具有B样条的若干性质，还放松了曲线光滑性的要求，将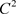连续松弛为连续。该样条还提供了形状控制参数，可以不改变控制顶点而通过改变形状控制参数来实现对曲线的控制。1990年Barsky [3] 等改进几何方法构造样条曲线，给出了Beta样条曲线定义。紧接着，Joe [4] 提出含有三个参数的Beta样条曲线，并分析了参数对样条曲线的影响。Nur [5] 等提出了一种含有一个参数的三角函数Beta样条曲线，使得Beta样条曲线具有更好的光滑性。

1985年Shoemake [6] 最先提出了一种构造四元数曲线的方法。其将n维欧氏空间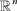中Bézier曲线的线性插值(即经典De Casteljau算法)转变为球面线性插值，构造出单位四元数Bézier曲线，这种构造方式自然地扩展到m维球面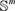中任意次曲线上。Kim [8] 给出了单位四元数曲线一阶导数的微分公式，该公式只适用于单位四元数的一阶导数。在此基础上，Kim [9] 提出一类新的单位四元数曲线，通过将样条曲线基函数的累加形式转化为累积形式来构造相应的四元数曲线，该曲线保留了欧氏空间中样条曲线的微分性质，具有高阶导矢。2004年Nielson [10] 将样条曲线推广到四元数空间，通过改变张力参数和节点间距，使得样条曲线具有更加灵活的形状调控能力。邢燕 [11] [12] 通过选取适当的多项式调配函数，分别构造了和连续的四元数样条曲线，檀结庆 [13] 构造了基于参数五次多项式的单位四元数样条曲线，对给定数据点进行精确插值，并且引入局部张力参数，通过改变参数影响局部曲线形状。孙楠 [14] 在此基础上，给出Bézier四元数样条曲线端点处的高阶导矢计算公式，并构造出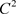连续的四元数样条曲线。

基于此，本文在Kim研究的基础上，将欧氏空间中Beta样条曲线与四元数结合起来推广到四元数空间中，构造Beta四元数样条曲线，该曲线可以通过改变各节点的形状参数，从而局部调整样条曲线的形状，为刚体旋转运动的运动轨迹设计提供新方法。

2. 预备知识

2.1. Beta样条曲线

给定三维欧氏空间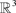中的多边形顶点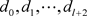，两组参数，，按如下步骤定义顶点。

首先定义内顶点：

，

。

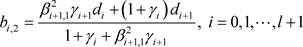其次定义首末顶点：

$b_{i,3}=\{\begin{array}{l}\frac{{\beta }_{i+1,1}{b}_{i,2}+b_{i+1,1}}{1+{\beta }_{i+1,1}}\text{,}i=0,1,\cdots ,l,\\ 0,i=l+1,\end{array}$

其中 ${\gamma }_i=\frac{2\left(1+{\beta }_{i,1}\right)}{{\beta }_{i,2}+2{\beta }_{i,1}\left(1+{\beta }_{i,1}\right)}$。

以点 $b_{i,j}\left(j=0,1,2,3;i=1,2,\cdots ,l\right)$ 为控制顶点构造的Bézier样条曲线，称为三次Beta样条曲线 [15]，其第i段表达式为

$s_i\left(t\right)={\displaystyle \underset{j=0}{\overset{3}{\sum }}{b}_{i,j}{B}_{j,3}\left(t\right),t\in \left[0,1\right]}$，

其中 $B_{j,3}\left(t\right)=C_3^j{t}^j{\left(1-t\right)}^{3-j}$ 是Bernstein函数。称 $d_i$ 为辅助控制顶点， $b_{i,j}$ 为控制顶点， ${\beta }_{i,1}$ 和 ${\beta }_{i,2}$ 为形状参数。

若令两组形状参数 ${\beta }_{i,1}=1$ 和 ${\beta }_{i,2}=0$，则三次Beta样条曲线退化为三次B样条曲线。

欧氏空间中Beta样条曲线是 $G^2$ 的。由几何连续性定义 [1] 可知，Beta样条曲线满足以下Beta约束式：

i) $s_i\left(0\right)=s_{i-1}\left(1\right)$ ；

ii) 存在 ${\xi }_i>0$，使得 ${s^{\prime }}_i\left(0\right)={\xi }_i{s^{\prime }}_{i-1}\left(1\right)$ ；

iii) 存在 ${\delta }_i\in \text{R}$，使得 ${s^{″}}_i\left(0\right)={\xi }_i^2{s^{″}}_{i-1}\left(1\right)+{\delta }_i{s^{\prime }}_{i-1}\left(1\right)$。

2.2. 四元数

称 $q=w+xi+yj+zk\in {\mathbb{S}}^3$ 为一个四元数，其中 $w,x,y,z\in R$， $i,j,k$ 为不同的虚数单位，且满足

$i^2=j^2=k^2=-1$， $ij=-ji=k$， $jk=-kj=i$， $ki=-ik=j$。

四元数也可以表示成 $\left(w,x,y,z\right)$。

给定四元数 $q_i=\left(w_i,x_i,y_i,z_i\right),i=1,2$。四元数有如下运算 [6]。

四元数的加减：

$q_1\pm q_2=\left(w_1\pm w_2\right)+\left(x_1\pm x_2\right)i+\left(y_1\pm y_2\right)k+\left(z_1\pm z_2\right)k$。

四元数的乘法：

$\begin{array}{l}{q}_1{q}_2=\left(w_1{w}_2-x_1{x}_2-y_1{y}_2-z_1{z}_2\right)+\left(w_1{x}_2+x_1{w}_2+y_{1}z{}_2-z_1{y}_2\right)i\\ +\left(w_1{y}_2+y_1{w}_2+z_1{x}_2-x_1{z}_2\right)j+\left(w_1{z}_1+z_1{w}_2+x_1{y}_2-y_1{x}_2\right)k.\end{array}$

注意的是四元数乘法不满足交换律。

四元数的逆：

$q^{-1}=\left(w,-x,-y,-z\right)$。

给定单位四元数 $q=\left(w,x,y,z\right)$，即 $w^2+x^2+y^2+z^2=1$。令

$\theta =\arccos w\in \left[0,\pi \right]$，

$\left(a,b,c\right)=\frac{\left(x,y,z\right)}{\sqrt{x^2+y^2+z^2}}\in {\mathbb{S}}^2$，

经过简单的计算，单位四元数q还可以表示为 [6]

$q=\left(\cos \theta ,\sin \theta \cdot \left(a,b,c\right)\right)$。

对于单位四元数 $p=\left(\cos \theta ,v\sin \theta \right)$，其中 $v=\left(a,b,c\right)\in {\mathbb{S}}^2$，其对数映射为 [8]

$\log \left(p\right)=\left(0,\theta v\right)$。

则有以下等式成立：

$\log {\left(p\right)}^n=n\log \left(p\right),n\in \left[0,1\right]$。

2.3. 四元数曲线

Shoemake [6] 提供了 ${\mathbb{S}}^3$ 空间中两个单位四元数 $q_1$ 和 $q_2$ 之间的最短路径的计算方法，即

${\gamma }_{q_1,q_2}\left(t\right)=q_1{\left(q_1^{-1}{q}_2\right)}^t,t\in \left[0,1\right]$。 (1)

引理1 [7] 给定单位四元数 $q_1$ 和 $q_2$，连接两点的单位四元数曲线有以下等价表示形式：

${\gamma }_{q_1,q_2}\left(t\right)=q_2{\left(q_2^{-1}{q}_1\right)}^{1-t}={\left(q_2^{-1}{q}_1\right)}^t{q}_1={\left(q_1^{-1}{q}_2\right)}^{1-t}{q}_2$。 (2)

当 $q_1=\left(1,0,0,0\right)$ 时，Kim [8] 给出了上述单位四元数曲线的一阶微分公式

${{\gamma }^{\prime }}_{1,q}\left(t\right)=\log \left(q\right){\gamma }_{1,q}\left(t\right)$。 (3)

其中 $q\in {\mathbb{S}}^3$。

在此基础上，Kim [9] 等人在对单位四元数曲线的研究中，给出了一种单位四元数曲线的一般构造方案。首先将以基函数 $B_i$ 和控制顶点 $p_i$ 构造的样条曲线的基本形式 $p\left(t\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}{p}_i{B}_i\left(t\right)}$，转化为累加形式

$p\left(t\right)=p_0{\tilde{B}}_0\left(t\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\Delta p_i{\tilde{B}}_i}\left(t\right),t\in \left[0,1\right]$。

其中 ${\tilde{B}}_i\left(t\right)={\displaystyle \underset{j=i}{\overset{n}{\sum }}{B}_i\left(t\right)}$。再通过Kim提供的构造方法，利用四元数的对数与指数运算，得到相应的单位四元数曲线为

$q\left(t\right)=q_0^{{\tilde{B}}_0\left(t\right)}{\displaystyle \underset{i=1}{\overset{n}{\prod }}{\left(q_{i-1}^{-1}{q}_i\right)}^{{\tilde{B}}_i\left(t\right)}},t\in \left[0,1\right]$。

其中 $q_i\in {\mathbb{S}}^3$ 为控制顶点。

3. Beta四元数样条曲线

3.1. Beta四元数样条曲线的构造

在本节中，我们将欧氏空间中的Beta样条曲线转化为具有累积形式的单位四元数样条曲线。

给定四元数顶点 $p_0,p_1,\cdots ,p_{l+2}\in {\mathbb{S}}^3$ 以及两组参数 ${\beta }_{0.1},{\beta }_{1,1},\cdots ,{\beta }_{l+1,1}>0$， ${\beta }_{0,2},{\beta }_{1,2},\cdots ,{\beta }_{l+1,2}\in ℝ$，按如下步骤定义顶点。

首先定义内顶点：

$q_{i,1}=p_i{\left(p_i^{-1}{p}_{i+1}\right)}^{{\gamma }_i/{\Delta }_i},i=0,1,\cdots ,l+1$，

$q_{i,2}=p_i{\left(p_i^{-1}{p}_{i+1}\right)}^{\left({\gamma }_i+1\right)/{\Delta }_i},i=0,1,\cdots ,l+1$。

其次定义首末顶点：

$q_{i,0}=\{\begin{array}{l}{q}_{i-1,2}{\left(q_{i-1,2}^{-1}{q}_{i,1}\right)}^{1/\left(1+{\beta }_{i,1}\right)}\text{,}i=1,2,\cdots ,l+1,\\ 0,i=0,\end{array}$

$q_{i,3}=\{\begin{array}{l}{q}_{i,2}{\left(q_{i,2}^{-1}{q}_{i+1,1}\right)}^{1/\left(1+{\beta }_{i+1,1}\right)}\text{,}i=0,1,\cdots ,l,\\ 0,i=l+1,\end{array}$

其中 ${\Delta }_i={\gamma }_i+1+{\beta }_{i+1,1}^2{\gamma }_{i+1}$， ${\gamma }_i=\frac{2\left(1+{\beta }_{i,1}\right)}{{\beta }_{i,2}+2{\beta }_{i,1}\left(1+{\beta }_{i,1}\right)}$。显然 $q_{i,3}=q_{i+1,0}$。为了便于大家理解，我们给出了点 $q_{i,j}$ 在三维空间的构造示意图，如图1所示。

Figure 1. Control point construction diagram

图1. 控制顶点构造示意图

引理2 对于上述方式定义的点 $q_{i,j}\left(j=0,1,2,3;i=1,2,\cdots ,l\right)$，有以下关系式成立：

i) $\log \left(p_i^{-1}{q}_{i,1}\right)={\gamma }_i\log \left(q_{i,1}^{-1}{q}_{i,2}\right)$，

ii) $\log \left(q_{i-1,2}^{-1}{p}_i\right)={\beta }_{i,1}^2{\gamma }_i\log \left(q_{i-1,1}^{-1}{q}_{i-1,2}\right)$，

iii) $\log \left(q_{i,0}^{-1}{q}_{i,1}\right)={\beta }_{i,1}\log \left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)$。

证明：由点 $q_{i,j}$ 的定义方式即可验证上述关系式成立。

定义1 由点 $q_{i,j}\left(j=0,1,2,3;i=1,2,\cdots ,l\right)$ 生成的四元数样条曲线，称为Beta四元数样条曲线。其第i段曲线表示为：

$s_i\left(t\right)=q_{i,0}{\displaystyle \underset{j=1}{\overset{3}{\prod }}{\left(q_{i,j-1}^{-1}{q}_{i,j}\right)}^{{\tilde{B}}_{j,3}\left(t\right)}},t\in \left[0,1\right]$。 (4)

其中 ${\tilde{B}}_{j,3}={\displaystyle \underset{i=j}{\overset{3}{\sum }}{B}_{i,3}},j=1,2,3$，称 $p_i$ 为辅助控制顶点， $q_{i,j}$ 为控制顶点， ${\beta }_{i,1}$ 和 ${\beta }_{i,2}$ 为形状参数， $s_i\left(t\right)$ 为第i段Beta四元数曲线。

3.2. Beta四元数样条曲线性质

3.2.1. Beta四元数样条曲线一阶微分性质

Beta四元数样条曲线保持了欧氏空间中Beta样条曲线的许多重要微分性质。由于所构造的曲线是由l条四元数曲线段构成，且每一段都是光滑多项式函数和光滑指数函数的复合函数的乘积，因此研究样条曲线连接点处的光滑性即可。在这里，我们给出Beta四元数样条曲线 $G^1$ 连续性的证明。

定理1 Beta四元数曲线 $s_i\left(t\right),i=1,2,\cdots ,l;t\in \left[0,1\right]$，在连接点处是 $G^1$ 连续的。

证明：将 $t=0$ 和 $t=1$ 分别代入式(4)，可以得

$\begin{array}{l}{s}_i\left(0\right)=q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(0\right)}{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(0\right)}{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(0\right)}=q_{i,0},\\ s_i\left(1\right)=q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(1\right)}{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(1\right)}{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(1\right)}=q_{i,3},\end{array}$ (5)

因此，曲线 $s_i\left(t\right)$ 的两个端点是 $q_{i,0}$ 和 $q_{i,3}$。由 $s_i\left(0\right)=s_{i-1}\left(1\right)$ 可证明Beta四元数样条曲线是 $G^0$ 连续的。

对曲线 $s_i\left(t\right)$ 关于参数t求一阶导矢得

$\begin{array}{l}{s^{\prime }}_i\left(t\right)=q_{i,0}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}\right]}^{\prime }{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\\ +q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime }{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\\ +q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\right]}^{\prime },\end{array}$ (6)

其中

$\begin{array}{l}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}\right]}^{\prime }={\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{{\tilde{B}}^{\prime }}_{1,3}\left(t\right)\log \left(q_{i,0}^{-1}{q}_{i,1}\right),\\ {\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime }={\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{{\tilde{B}}^{\prime }}_{2,3}\left(t\right)\log \left(q_{i,1}^{-1}{q}_{i,2}\right),\\ {\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\right]}^{\prime }={\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}{{\tilde{B}}^{\prime }}_{3,3}\left(t\right)\log \left(q_{i,2}^{-1}{q}_{i,3}\right),\end{array}$

且

$\begin{array}{l}{\tilde{B}}_{1,3}\left(t\right)=1-{\left(1-t\right)}^3\text{,}{{\tilde{B}}^{\prime }}_{1,3}=3{\left(1-t\right)}^2,\\ {\tilde{B}}_{2,3}\left(t\right)=-2t^3+3t^2\text{,}{\widetilde{B^{\prime }}}_{2,3}=6t\left(1-t\right),\\ {\tilde{B}}_{3,3}\left(t\right)=t^3\text{,}{\widetilde{B^{\prime }}}_{3,3}=3t^2,\end{array}$

将 $t=0$ 和 $t=1$ 分别代入式(6)，可得

$\begin{array}{l}{s^{\prime }}_i\left(0\right)=3q_{i,0}\log \left(q_{i,0}^{-1}{q}_{i,1}\right),\\ {s^{\prime }}_i\left(1\right)=3q_{i,3}\log \left(q_{i,2}^{-1}{q}_{i,3}\right),\end{array}$ (7)

由引理1可知

$\begin{array}{l}{q}_{i,0}=q_{i,1}{\left(q_{i,1}^{-1}{q}_{i-1,2}\right)}^{\frac{{\beta }_{i,1}}{1+{\beta }_{i,1}}},\\ q_{i,3}=q_{i,2}{\left(q_{i,2}^{-1}{q}_{i+1,1}\right)}^{\frac{1}{1+{\beta }_{i+1,1}}},\end{array}$

分别代入(7)得

$\begin{array}{l}{s^{\prime }}_i\left(0\right)=\frac{3{\beta }_{i,1}}{1+{\beta }_{i,1}}{q}_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i,1}\right),\\ {s^{\prime }}_i\left(1\right)=\frac{3}{1+{\beta }_{i+1,1}}{q}_{i,3}\log \left(q_{i,2}^{-1}{q}_{i+1,1}\right),\end{array}$

通过计算得

${s^{\prime }}_i\left(0\right)={\beta }_{i,1}{s^{\prime }}_{i-1}\left(1\right)$。 (8)

由一阶Beta约束可知，Beta四元数样条曲线是 $G^1$ 连续的。特殊地，当 ${\beta }_{i,1}=1$， ${\beta }_{i,2}=0$ 时，相应的四元数样条曲线是 $C^1$ 连续的。

3.2.2. Beta四元数样条曲线二阶微分性质

上一节，我们证明了Beta四元数样条曲线是 $G^1$ 连续的。接下来，我们研究Beta四元数样条曲线二阶微分相关性质。在欧氏空间中，若使组合Bézier曲线 $G^2$ 连续，必须保证两曲线在公共连接点的左右导矢满足二阶Beta约束。在四元数空间中同样适用。

引理3 给定单位四元数 $q_1$ 和 $q_2$ 以及连接这两点的单位四元数曲线 ${\gamma }_{q_1,q_2}\left(t\right)$，则有以下等式成立：

$\log \left(q_2{q}_1^{-1}\right)\cdot {\gamma }_{q_1,q_2}\left(t\right)={\gamma }_{q_1,q_2}\left(t\right)\cdot \log \left(q_1^{-1}{q}_2\right),t\in \left[0,1\right]$。 (9)

证明：由式(1)可知

${\gamma }_{q_1,q_2}\left(t\right)=q_1{\gamma }_{1,q_1^{-1}{q}_2}\left(t\right)$，

由式(3)可知

${{\gamma }^{\prime }}_{q_1,q_2}\left(t\right)=q_1{{\gamma }^{\prime }}_{1,q_1^{-1}{q}_2}\left(t\right)={\gamma }_{q_1,q_2}\left(t\right)\log \left(q_1^{-1}{q}_2\right)$。

由引理1可知

${\gamma }_{q_1,q_2}\left(t\right)={\left(q_2^{-1}{q}_1\right)}^t{q}_1$，

同理可证

${{\gamma }^{\prime }}_{q_1,q_2}\left(t\right)=\log \left(q_2{q}_1^{-1}\right){\gamma }_{q_1,q_2}\left(t\right)$，

由此即可证明引理。

实际上，式(9)为单位四元数曲线 ${\gamma }_{q_1,q_2}\left(t\right)$ 一阶导矢。

定理2 Beta四元数曲线 $s_i\left(t\right),i=1,2,\cdots ,l;t\in \left[0,1\right]$，在连接点处 $G^2$ 连续的充分必要条件是

$q_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i,1}\right)=\frac{{\gamma }_i}{{\Delta }_i}{q}_{i,0}\log \left(p_i^{-1}{p}_{i+1}\right)+\frac{{\beta }_{i,1}^2{\gamma }_i}{{\Delta }_{i-1}}\log \left(p_{i-1}^{-1}{p}_i\right)q_{i-1,3}$。 (10)

证明：对曲线 $s_i\left(t\right)$ 关于参数t求二阶导矢可得

$\begin{array}{l}{s^{″}}_i\left(t\right)=q_{i,0}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{B_{1,3}\left(t\right)}\right]}^{\prime \text{}\prime }{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\\ +q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime \text{}\prime }{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\\ +q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{B_{1,3}\left(t\right)}{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{B_{2,3}\left(t\right)}{\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\right]}^{\prime \text{}\prime }\\ +2q_{i,0}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}\right]}^{\prime }{\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime }{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\\ +2q_{i,0}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{B_{1,3}\left(t\right)}\right]}^{\prime }{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\right]}^{\prime }\\ +2q_{i,0}{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime }{\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{B_{3,3}\left(t\right)}\right]}^{\prime },\end{array}$ (11)

其中

$\begin{array}{l}{\left[{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}\right]}^{\prime \text{}\prime }={\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{\left[{B^{\prime }}_{1,3}\left(t\right)\log \left(q_{i,0}^{-1}{q}_{i,1}\right)\right]}^2+{\left(q_{i,0}^{-1}{q}_{i,1}\right)}^{{\tilde{B}}_{1,3}\left(t\right)}{B^{″}}_{1,3}\left(t\right)\log \left(q_{i,0}^{-1}{q}_{i,1}\right),\\ {\left[{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}\right]}^{\prime \text{}\prime }={\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{\left[{B^{\prime }}_{2,3}\left(t\right)\log \left(q_{i,1}^{-1}{q}_{i,2}\right)\right]}^2+{\left(q_{i,1}^{-1}{q}_{i,2}\right)}^{{\tilde{B}}_{2,3}\left(t\right)}{B^{″}}_{2,3}\left(t\right)\log \left(q_{i,1}^{-1}{q}_{i,2}\right),\\ {\left[{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}\right]}^{\prime \text{}\prime }={\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}{\left[{B^{\prime }}_{3,3}\left(t\right)\log \left(q_{i,2}^{-1}{q}_{i,3}\right)\right]}^2+{\left(q_{i,2}^{-1}{q}_{i,3}\right)}^{{\tilde{B}}_{3,3}\left(t\right)}{B^{″}}_{3,3}\left(t\right)\log \left(q_{i,2}^{-1}{q}_{i,3}\right),\end{array}$

将 $t=0$ 和 $t=1$ 分别代入式(11)，可以得

$\begin{array}{l}{s^{″}}_i\left(0\right)=9q_{i,0}{\log }^2\left(q_{i,0}^{-1}{q}_{i,1}\right)-6q_{i,0}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)+6q_{i,0}\log \left(q_{i,1}^{-1}{q}_{i,2}\right),\\ {s^{″}}_i\left(1\right)=9q_{i,3}{\log }^2\left(q_{i,2}^{-1}{q}_{i,3}\right)+6q_{i,3}\log \left(q_{i,2}^{-1}{q}_{i,3}\right)-6q_{i,2}\log \left(q_{i,1}^{-1}{q}_{i,2}\right)q_{i,2}^{-1}{q}_{i,3},\end{array}$

由引理3，可将上式改写为

$\begin{array}{l}{s^{″}}_i\left(0\right)=9q_{i,0}{\log }^2\left(q_{i,0}^{-1}{q}_{i,1}\right)-6q_{i,0}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)+6q_{i,0}\log \left(q_{i,1}^{-1}{q}_{i,2}\right),\\ {s^{″}}_i\left(1\right)=9q_{i,3}{\log }^2\left(q_{i,2}^{-1}{q}_{i,3}\right)+6q_{i,3}\log \left(q_{i,2}^{-1}{q}_{i,3}\right)-6\log \left(q_{i,2}{q}_{i,1}^{-1}\right)q_{i,3},\end{array}$ (12)

由此可得曲线 $s_i\left(t\right)$ 首末端点处的二阶导矢。

首先证明必要性。由曲线控制顶点的构造可知，等式(10)可转化为

$\left(1+\frac{1}{{\beta }_{i,1}}\right)q_{i-1,3}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)=q_{i,0}\log \left(p_i^{-1}{q}_{i,1}\right)+\log \left(p_i{q}_{i-1,2}^{-1}\right)q_{i-1,3},$ (13)

等式两边同乘 $\frac{6}{{\gamma }_i}$ 得

$\frac{6\left(1+{\beta }_{i,1}\right)}{{\gamma }_i{\beta }_{i,1}}{q}_{i-1,3}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)=\frac{6}{{\gamma }_i}{q}_{i,0}\log \left(p_i^{-1}{q}_{i,2}\right)+\frac{6}{{\gamma }_i}\log \left(p_i{q}_{i-1,2}^{-1}\right)q_{i-1,3}$，

利用引理2的(i) (ii)，整理可得

$6\left(1+{\beta }_{i,1}+\frac{{\beta }_{i,2}}{2{\beta }_{i,1}}\right)q_{i-1,3}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)=6q_{i,0}\log \left(q_{i,1}^{-1}{q}_{i,2}\right)+6{\beta }_{i,1}^2\log \left(q_{i-1,2}{q}_{i-1,1}^{-1}\right)q_{i-1,3}$，

再利用引理2的(iii)可得

$\begin{array}{l}6q_{i-1,3}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)+6{\beta }_{i,1}^2{q}_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)+3{\beta }_{i,2}{q}_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)\\ =6q_{i,0}\log \left(q_{i,1}^{-1}{q}_{i,2}\right)+6{\beta }_{i,1}^2\log \left(q_{i-1,2}{q}_{i-1,1}^{-1}\right)q_{i-1,3},\end{array}$

上式两边加 $9q_{i,0}{\log }^2\left(q_{i,0}^{-1}{q}_{i,1}\right)$，由引理2的(iii)整理可得

$\begin{array}{l}9q_{i,0}{\log }^2\left(q_{i,0}^{-1}{q}_{i,1}\right)-6q_{i,0}\log \left(q_{i,0}^{-1}{q}_{i,1}\right)+6q_{i,0}\log \left(q_{i,1}^{-1}{q}_{i,2}\right)\\ ={\beta }_{i,1}^2\left(9q_{i-1,3}{\log }^2\left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)+6q_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)-6\log \left(q_{i-1,2}{q}_{i-1,1}^{-1}\right)q_{i-1,3}\right)\\ +{\beta }_{i,2}\left(3q_{i-1,3}\log \left(q_{i-1,2}^{-1}{q}_{i-1,3}\right)\right).\end{array}$

即 ${s^{″}}_i\left(0\right)={\beta }_{i,1}^2{s^{″}}_{i-1}\left(1\right)+{\beta }_{i,2}{s^{\prime }}_{i-1}\left(1\right)$，由此即可证明其必要性。

接着证明充分性。将式(7)和式(12)代入Beta约束条件(iii)，再利用引理2即可证明式(10)成立。

4. 实验

在这节中，我们通过数值实验来说明本文提出的Beta四元数样条曲线构造方法的可行性和有效性，并将其应用于刚体运动中。

例1 给定球面 ${\mathbb{S}}^3$ 上5个辅助控制顶点

$\begin{array}{l}{P}_0=\left(-0.2011-0.74780.07910.6278\right),\\ P_1=\left(-0.16030.60730.36530.6871\right),\\ P_2=\left(-0.46960.0554-0.8480-0.2394\right),\\ P_3=\left(-0.5268-0.5665-0.4194-0.4751\right),\\ P_4=\left(0.6921-0.25510.13140.6623\right),\end{array}$

以及形状控制参数 ${\beta }_{j,1}=1,{\beta }_{j,2}=0.5,j=0,\cdots ,4$，利用本文的构造方法，我们得到一组控制顶点

$\begin{array}{l}{q}_{1,0}=\left(-0.37960.45890.11060.7956\right),\\ q_{1,1}=\left(-0.46100.6671-0.15070.5655\right),\\ q_{1,2}=\left(-0.58940.4380-0.65430.1810\right),\\ q_{2,0}=q_{1,3}=\left(-0.60930.1514-0.7734-0.0877\right),\\ q_{2,1}=\left(-0.5263-0.1607-0.7619-0.3415\right),\\ q_{2,2}=\left(-0.5474-0.3901-0.6038-0.4284\right),\\ q_{2,3}=\left(-0.3509-0.7065-0.5548-0.2642\right),\end{array}$

由此八个控制顶点可构造两段相邻的Beta四元数曲线 $s_1\left(t\right)$ 和 $s_2\left(t\right)$， $t\in \left[0,1\right]$，其中曲线 $s_i\left(t\right)$ 的控制顶点为 $q_{i,0},q_{i,1},q_{i,2},q_{i,3},i=1,2$。

由式(7)可得到曲线 $s_1\left(t\right)$ 和 $s_2\left(t\right)$ 在 $t=0$ 和 $t=1$ 处的一阶导矢，经过计算可知满足式(8)。即给定插值点构造的Beta四元数样条曲线是 $G^1$ 连续的。由式(12)可得到曲线 $s_1\left(t\right)$ 和 $s_2\left(t\right)$ 在 $t=0$ 和 $t=1$ 处的二阶导矢，由一阶和二阶导矢计算可知，满足Beta约束条件(iii)，因此给定辅助控制顶点构造的Beta四元数样条曲线是 $G^2$ 连续的。

利用本文所给的定理2，将辅助控制顶点p，控制顶点q以及形状参数 $\beta$ 相应的点，直接代入式(10)，经过计算可知满足式(10)。即得给定插值点构造的Beta四元数曲线是 $G^2$ 连续的。由定理2即可直接证明曲线是 $G^2$ 连续的，无需求解样条曲线导矢。

基于四元数与旋转变换的关系 [16]，我们将上述Beta四元数样条曲线应用于刚体旋转运动的表示，得到了刚体中心的旋转运动轨迹，如图2所示。在此基础上，假定刚体的平移运动为直线运动，就可以得到图3所示的该运动的等时间离散表示，其中绿色立方体表示样条连接点处的姿态。

Figure 2. The rotational motion trajectory of the center of the rigid body

图2. 刚体中心的旋转运动轨迹

Figure 3. Schematic diagram of rigid body motion

图3. 刚体运动示意图

例2 给定球面 ${\mathbb{S}}^3$ 上5个辅助控制顶点

$\begin{array}{l}{P}_0=\left(0.6387-0.6301-0.33060.2927\right),\\ P_1=\left(0.4412-0.7009-0.55670.0646\right),\\ P_2=\left(-0.81800.50110.02490.2813\right),\\ P_3=\left(0.7494-0.5340-0.0433-0.3891\right),\\ P_4=\left(0.99140.03980.1179-0.0393\right),\end{array}$

令形状控制参数 ${\beta }_{j,1}=1,{\beta }_{j,2}=0.5,j=0,\cdots ,4$，利用本文的构造方法，我们得到一条Beta四元数样条曲线，将该Beta四元数样条曲线应用于刚体旋转运动的表示，得到了刚体中心的旋转运动轨迹，如图4所示。若改变形状参数 ${\beta }_{1,2}$ 的值，从图4可以看出样条曲线形状发生变化。

Figure 4. The effect of shape parameters ${\beta }_{1,2}$ on the shape of the spline, the corresponding ${\beta }_{1,2}$ values of red, black and blue curves are 4, 2 and 0.5 respectively

图4. 形状参数 ${\beta }_{1,2}$ 对样条曲线形状的影响，蓝，黑，红曲线分别对应 ${\beta }_{1,2}$ 的值为0.5, 2, 4

5. 总结

本文将欧氏空间中的Beta样条曲线推广到单位四元数空间，提出了一种构造Beta四元数样条曲线的方法，构造的样条曲线满足 $G^1$ 连续，并且给出了 $G^2$ 连续的充要条件。该方法直接由给定的辅助控制顶点以及形状相应的形状控制参数计算控制顶点，不需要迭代算法求解非线性方程组。在给定插值点不变的情况下，可以独立计算每段四元数样条曲线的控制顶点，并且可通过改变局部形状控制参数，调整四元数样条曲线形状。在后续的研究中，将会考虑如何选取形状控制参数使得曲线达到最优，以及如何进行Beta四元数样条曲线光滑拼接问题。

NOTES

^*通讯作者。