基于二维四值元胞自动机和混沌系统的图像加密算法

Image Encryption Algorithm Based on 2D Quaternary Cellular Automata and Chaotic System

摘要: 提出了一种结合改进的Logistic-PWLCM映射、超混沌Chen系统所生成的改进序列和二维四值元胞自动机的图像加密方法。将Logistic映射和PWLCM映射复合得到新的一维混沌系统，利用该系统和超混沌Chen系统所生成序列的改进，使得用于控制加密过程的密钥流序列具有更好的混沌特性。论文构造了一个新型的二维四值元胞自动机，对传统的二值元胞自动机做了推广，提高了元胞自动机演化的复杂性。用该元胞自动机和两个混沌系统设计了一个新的混沌图像加密算法，并做了详细的性能分析。实验结果和分析显示，本文所提出的图像加密算法具有较大的密钥空间和抵御多种攻击分析的优良性能。

Abstract: A chaotic image encryption algorithm which combines improved Logistic-PWLCM map, improved sequences generated by hyperchaotic Chen system and 2D quaternary cellular automata is proposed. In the proposed cryptosystem, Logistic map and PWLCM map are compound into a new map, and the sequences generated by hyperchaotic Chen system are improved, which makes the key streams controlling the encryption process have better chaotic nature. A new 2D quaternary cellular automata is constructed as well. The evolution complexity of the cellular automata is greatly enhanced. A new chaotic image encryption algorithm is designed using the proposed cellular au-tomata and two chaotic systems. Its security and performance are analyzed in detail. The experimental results and analysis show that the proposed image encryption algorithm has larger key space and good performances to resist various attacks.

1. 引言

在互联网飞速发展的信息时代，人们对于互联网的依赖也越来越多，人们通过互联网进行日常交流，如聊天、购物、浏览新闻等行为。在频繁地使用互联网的同时，使用者大量的个人信息也经常通过图像的传递在互联网中被不法分子传播和盗用，给使用者带来了极大的麻烦乃至实际的损害。如何保护个人信息的安全也就成了无法逃避的问题。图像作为传递信息的一种重要媒介，图像加密自然也就作为一种有效保护信息的方法进入人们的视线。

元胞自动机(CA)是一种时间和空间都离散的动力系统。散布在规则格网中的每一个元胞取值有限的离散状态，遵循同样的作用规则，依据确定的局部规则作同步更新。大量的元胞通过邻域元胞的简单相互作用而构成动态系统的演化 [1]。由于其简单的规则结构、局部交互、类随机行为和大规模并行性，CA在图像加密领域具有独特的优势 [2]。CA可以比现有的混沌序列发生器更快地生成随机和混沌的序列，它使用基于每个邻域元胞的当前状态值的局部变换，使得CA实现非常简单，并且消耗资源更少 [3]。使用CA进行作用的过程称为CA演化。陈祥等人 [4] 使用二维Henon离散混沌系统与一维CA结合，在图像加密的过程中，使用混沌序列决定不同的CA演化的规则号，生成一个不可逆的元胞序列，并与明文图像分别作行和列的异或从而达到加密效果，摆脱了传统的置乱–扩散结构的同时，密文图像也具有很高的安全性。李凯佳 [5] 提出一维的记忆CA，结合DNA异或将置乱完成的明文图像进行扩散。Abolfazl等人 [6] 同样利用一维的CA对图像进行加密，同时加入了置乱步骤；将二维的Arnold变换改进成三维模型，应用三维Arnold变换产生混沌序列，利用混沌序列的排列索引，对CA演化后的图像矩阵进行置乱。在一维CA中，大部分的CA演化规则都是不可逆且随机的，但也存在部分规则，使得演化任意元胞一定次数后回归到原始的状态。基于这个想法，冯志华 [7] 提出了基于可逆CA的图像加密算法。而平萍 [8] [9]、薛帅 [10] 和张星 [11] 则各自分别描述了一维二阶可逆的CA，并设计了基于可逆CA的加密算法。

一维CA动力学性质较二维CA来说相对简单，大多数一维CA存在规则空间小、扩散率低以及没有明确CA规则分类等固有缺陷 [2]。为了增加CA的复杂性，更多的研究者开始将二维CA使用到图像加密中。张统权 [12] 提出了一种Von Neumann型的耦合二维触发CA。柴宗谦 [13] 则提出了一种X型邻域的变种X2型邻域的二维可逆CA。而在二维CA的几种邻域型基中，Von Neumann型CA的图像加密技术则拥有更大的密钥空间。李玲等 [14] 人在分析CA的混沌和密码学性质的基础上构造一个二维伪随机数矩阵来进行图像加密。李辉亮等 [1] [15] 将二维Von Neumann型CA融入到图像置乱和水印的算法中。以往的二维CA加密方法中大多数学者都是将CA运用到混沌映射产生的混沌序列上，即将混沌序列做CA演化，再与明文图像异或进行加密，解密时同样需要用混沌序列做CA演化以求得明文。Ping等人 [2] 使用仿生的二维Von Neumann型CA到图像加密的扩散步骤中，他们提出了一种可逆的元胞自动机加密方法，可直接将明文进行多次CA演化，解密时直接使用密文图像进行CA演化解密得到明文图像。Satyabrata等人 [3] 提出二维CA的数学模型，使用不同的CA演化规则对不同位置的元胞进行二维的CA演化，利用某一些特定的规则矩阵在演化任意元胞矩阵一定次数后会回归自身的特性，对图像进行加密解密。

在综合分析上述各种算法的优缺点的基础上，本文提出一种更为安全的图像加密方案。首先将Logistic映射和PWLCM映射复合，得到一种新的混沌映射Logistic-PWLCM，简称LPWLCM。对生成的序列所作的SP800-22测试结果表明该复合映射所生成的序列的伪随机性能很好，通过了所有15种测试。本文改进了超混沌Chen系统所生成的混沌序列，使改进序列具有更好的伪随机性。本文还提出一种新的二维Von Neumann型的四值CA，该CA比传统的CA具有更复杂的演化行为，随机选取任意矩阵利用该CA演化，演化后的效果具有很好的伪随机性能。利用LPWLCM、超混沌Chen系统的改进序列和四值CA，本文提出了一种新的混沌图像加密算法。首先使用超混沌Chen系统产生的序列改进所得的密钥流对明文图像进行基于排序的位置置换得到置乱图像，应用四值CA分别演化LPWLCM所生成的密钥流以及置乱图像，得到两个四进制矩阵，再作进一步的比特异或扩散处理，得到密文图像。对算法的安全性能分析结果表明，本文所提出的加密算法具有优良的安全性能，能抵御多种攻击分析。

2. 预备知识

2.1. LPWLCM映射

Logistic又称为虫口模型，如(1)所示：

$x_{n+1}=a{x}_n\left[1-x_n\right]$ (1)

其中a为控制参数， $x_n\in \left(0,1\right)$， $a\in \left(0,4\right]$。当 $a\in \left(3.5699456,4\right]$ 时，由Logistic映射迭代得到的序列处于混沌状态。

PWLCM映射即分段线性映射(2)：

$x_{n+1}=\{\begin{array}{l}\frac{x_n}{p},x_n\in \left[0,p\right)\\ \frac{1-x_n}{1-p},x_n\in \left(p,1\right)\end{array}$ (2)

其中 $x_n\in \left(0,1\right)$，p为控制参数。当 $p\in \left(0,1\right)$ 时，该映射所生成的序列处于混沌状态。

一维混沌映射的混沌特性一般较弱，其混沌参数范围较小，多个一维简单混沌映射的复合可以提升单个一维混沌映射的动力学复杂性 [16]。为了提高Logistic映射和PWLCM映射的动力学性质，将两个映射复合成一个新的混沌映射(3)：

$x_{n+1}=\{\begin{array}{l}\frac{a{x}_n\left(1-x_n\right)}{p},\text{}a{x}_n\left(1-x_n\right)\in \left(0,p\right),\\ \frac{1-a{x}_n\left(1-x_n\right)}{1-p},\text{}\text{}\text{}a{x}_n\left(1-x_n\right)\in \left[p,1\right),\end{array}$ (3)

其中 $x_n\in \left(0,1\right)$， $a\in \left(0,4\right)$， $p\in \left(0,1\right)$。由于Logistic映射和PWLCM映射的取值范围都是 $\left(0,1\right)$，故可以直接复合而不需要做其他处理。图1为 $a=3.99$, $p=0.618$ 时LPWLCM的图形。

Figure 1. Graph of LPWLCM map

图1. LPWLCM映射的图形

采用NIST SP800-22对复合映射(3)所生成序列的随机性做了测试。NIST SP800-22是美国NIST (National Institute of Standards and Technology)发布的一系列关于信息安全的指南，SP800-22测试是用来检验用于加密系统的比特序列的随机特性，包括15种测试方法。每种测试计算一个或多个P-value，若P-value ≥ 0.01则认为通过该测试，认为序列具有随机性，反之则测试失败，序列是非随机的。将LPWLCM生成的序列采用式(4)量化得到比特流：

$t^{*}=\mathrm{mod}\left(floor\left(t\right)\times 2^{16},2\right)$ (4)

其中t为由LPWLCM迭代10⁶次所得到的序列， $t\in \left(0,1\right)$， $t^{*}\in \left\{0,1\right\}$。对 $t^{*}$ 进行SP800-22测试。通过表1测试结果可以看到，该系统通过SP800-22的15种测试，可以认为该混沌系统具有较好随机性。

Table 1. SP800-22 test for LPWLCM

表1. LPWLCM的SP800-22测试表

2.2. 超混沌Chen系统

本文对超混沌Chen系统(5)所生成的序列进行改进，提高其伪随机性。

$\{\begin{array}{l}\stackrel{\dot{}}{x}=a\left(y-x\right)\\ \stackrel{\dot{}}{y}=-xz+dx+cy-q\\ \stackrel{\dot{}}{z}=xy-bz\\ \stackrel{\dot{}}{q}=x+k\end{array}$ (5)

当 $a=36$， $b=3$， $c=28$， $d=-16$， $-0.7\le k\le 0.7$ 时，系统处于混沌状态。当 $k=0.2$ 时，该混沌系统中的4个Lyapunov指数依次为： ${\lambda }_1=1.552$， ${\lambda }_2=0.023$， ${\lambda }_3=0$， ${\lambda }_4=-12.573$。使用四阶龙格–库塔方法对其进行离散化处理，得到四个混沌序列 $\left\{x_i,y_i,z_i,q_i\right\}$， $i=1,2,3,\cdots ,n$。一个随机性良好的时间序列应该表现出类似噪声的随机特性，时间序列类似分形曲线，而不是相对光滑的曲线，其自相关系数函数接近 $\delta$ 函数；同一个混沌动力系统的不同状态变量的时间序列之间的互相关系数函数应接近于零函数 [17]。为了使超混沌Chen系统生成的状态时间序列序列具有更好的随机性，本文将超混沌陈系统所生成的序列进行改进，改进公式见(6)：

$s_i^{*}=s_i\times {10}^{12}-floor\left(s_i\times {10}^{12}\right).$ (6)

$s_i\in \left\{x_i,y_i,z_i,q_i\right\}$， $i=1,2,3,\cdots ,n$。函数 $floor\left(x\right)$ 为向下取整函数，因此 $s_i^{*}\in \left[0,1\right)$。图2为超混沌Chen系统所生成的状态时间序列改进前后的自相关系数图、互相关系数图，包括状态变量x的时间序列图、自相关系数图，序列x和序列y的互相关系数图。从图2中可以看出改进后的混沌序列随机性更好。

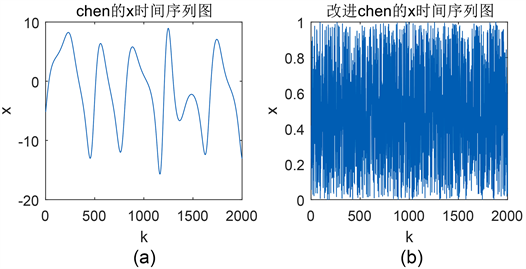
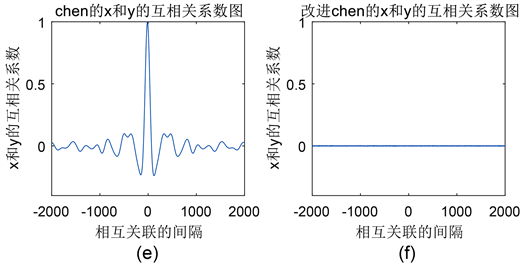
Figure 2. Performance test comparison of the sequences generated by the hyperchaotic Chen system before and after improvement: (a), (b) are the x time series diagrams; (c), (d) are the autocorrelation coefficient graphs of x; (e), (f) are the cross-correlation coefficient graphs between x and y

图2. 超混沌Chen系统所生成序列改进前后性能测试对比：(a)，(b) 分别为改进前后x的时间序列图；(c)，(d) 分别为改进前后x的自相关系数图；(e)，(f) 分别为改进前后x和y的互相关系数图

2.3. 二维四值CA

元胞自动机是一种原理简单，行为复杂的数学模型。元胞自动机的变化是按一定的规则通过自身以及其周围元胞的状态来更新自身的状态。本文考虑的是二维的元胞自动机。在二维的平面上，通常有两种类型的邻域：Von Neumann型邻域和摩尔型邻域 [2]，如图3所示。为了模拟无限边界的情况，对于边界上的元胞我们需要给它们加上外围的附加边界，类型有周期型边界和零边界。

(a) (b)

Figure 3. Two types of cellular automata: (a) Von Neumann type; (b) Moore type

图3. 两种元胞自动机：(a) Von Neumann型；(b) 摩尔型

本文提出一种新型二维四值CA模型如(7)所示，属于Von Neumann型CA，演化规则号 $1\le w\le 4^9-1$。

$\begin{array}{c}{S}_{i,j}^{n+1}=f_w\left(S_{i-1,j-1}^n,S_{i-1,j}^n,S_{i-1,j+1}^n,S_{i,j-1}^n,S_{i,j}^n,S_{i,j+1}^n,S_{i+1,j-1}^n,S_{i+1,j}^n,S_{i+1,j+1}^n\right)\\ =\mathrm{mod}(w_1\times S_{i-1,j-1}^n+w_2\times S_{i-1,j}^n+w_3\times S_{i-1,j+1}^n+w_4\times S_{i,j-1}^n+w_5\times S_{i,j}^n+w_6\times S_{i,j+1}^n\\ +w_7\times S_{i+1,j-1}^n+w_8\times S_{i+1,j}^n+w_9\times S_{i+1,j+1}^n,4),\end{array}$ (7)

其中 $S_{i,j}^n$ 表示在n时刻时处于位置 $\left(i,j\right)$ 的元胞S， $S_{i,j}^n\in \left\{0,1,2,3\right\}$， $f_w$ 表示在加权规则号为w下的元胞自动机演化规则。该模型与以往模型不同之处在于，在常规的元胞自动机中 $S\in \left\{0,1\right\}$，而在本文提出的四值元胞自动机中 $S\in \left\{0,1,2,3\right\}$，元胞S的状态取值空间变大，使得元胞自动机的演化规则更多，在演化过程中的动力学表现更复杂，并且在加权规则w的扰动下，该元胞自动机的演化行为变得更加不可预测。

在该元胞自动机下，首先将加权规则号w由十进制数转化成一个四进制数，然后利用上面提出的方法对元胞 $S_{i,j}^n$ 以及其周围的元胞一起作加权操作。例如，当 $w={\left(25699\right)}_{10}={\left(012101203\right)}_4$，对应加权规则为

$w=w_9{w}_8{w}_7{w}_6{w}_5{w}_4{w}_3{w}_2{w}_1=012101203$。若中心元胞 $S_{i,j}^0=0$ 及其周围的8个元胞值的矩阵为 $\left[\begin{array}{ccc}2& 2& 3\\ 1& 0& 1\\ 3& 2& 2\end{array}\right]$，

经过演化后中心元胞变成2：

$\begin{array}{c}{S}_{i,j}^1=\mathrm{mod}\left(2\times 3+2\times 0+3\times 2+1\times 1+0\times 0+1\times 1+3\times 2+2\times 1+2\times 0,4\right)\\ =\mathrm{mod}\left(6+0+6+1+0+1+6+2+0,4\right)=2.\end{array}$

对其他位置的元胞，均作类似的处理。

3. 加密方法

本文所提出的加密算法流程见图4。由改进的LPWLCM映射和超混沌Chen系统根据密钥 $K=\left\{x,p,a,chen\_x_0,chen\_y_0,chen\_z_0,chen\_q_0\right\}$，分别产生密钥流序列S和X。首先使用改进的超混沌Chen系统产生的密钥流X对明文图像P进行行和列的初步置乱得到矩阵 $P_1$，再利用四值CA将密钥流S演化得到四值密钥流SS。然后将置乱完成的图像 $P_1$ 转换为四值矩阵I，使用四值CA将其演化得到四值矩阵R，将四值密钥流SS与R做扩散处理得到四值矩阵RR，最后将RR转换成十进制的矩阵，得到密文图像矩阵C。

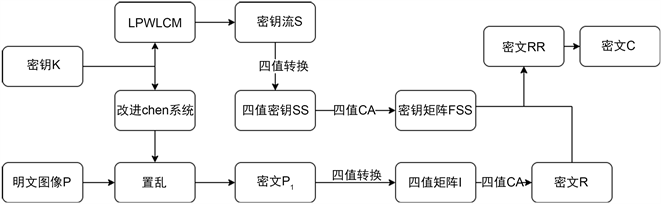
Figure 4. Encryption algorithm flow chart

图4. 加密算法流程图

3.1. 密钥流生成

模拟的图像大小假设为 $M\times N$，密钥流生成过程如下。

Step 1. 使用随机密钥K中的 $x,p,a$，通过LPWLCM映射生成大小为 $M\times N+500$ 的混沌序列，去掉前500个过渡值得到序列 $S^0$， $S^0=\left\{s_1^0,s_2^0,\cdots ,s_{M\times N}^0\right\}$。

Step 2. 通过量化公式(8)得到序列S， $S\in \left\{0,1,2,\cdots ,255\right\}$。

$S=floor\left(\mathrm{mod}\left(\mathrm{mod}\left(S^0\times {10}^{12},1\right)\times {10}^4,256\right)\right).$ (8)

Step 3. 将序列S每个分量转换为四进制，由于 $S\in \left\{0,1,2,\cdots ,255\right\}$，故序列S可以转化为大小是 $M\times 4N$ 的四值矩阵SS。

Step 4. 使用本文的四值CA将四值密钥流矩阵SS进行演化，得到新的四值密钥流矩阵FSS。FSS将在扩散步骤中使用。

Step 5. 使用明文图像P的像素值对随机密钥K中的 $chen\_x_0,chen\_y_0,chen\_z_0,chen\_q_0$ 进行干扰，使加密算法所使用的密钥流具有更强的明文敏感性，增强抵御差分攻击，已知明文/选择明文攻击的能力。修正公式见(9)。

$\{\begin{array}{l}{x}_0=chen\_x_0+\mathrm{mod}\left(sum\left(P\left(:,:\right)\times {10}^{-4}\right),0.1\right)\\ y_0=chen\_y_0+\mathrm{mod}\left(sum\left(P\left(:,:\right)\times {10}^{-5}\right),0.1\right)\\ z_0=chen\_z_0+\mathrm{mod}\left(sum\left(P\left(:,:\right)\times {10}^{-6}\right),0.1\right)\\ q_0=chen\_q_0+\mathrm{mod}\left(sum\left(P\left(:,:\right)\times {10}^{-7}\right),0.1\right)\end{array}$ (9)

其中 $sum\left(P\left(:,:\right)\right)$ 是指图像P中所有像素值之和。

Step 6. 应用公式(9)生成的 $x_0$， $y_0$， $z_0$， $q_0$ 以及超混沌Chen系统生成大小为 $M\times N+500$ 的改进混沌序列 $X_n$， $Y_n$， $Z_n$， $Q_n$，去掉四组序列的前500个过渡态，得到大小为 $M\times N$ 的四个随机序列：

$X_n=\left\{x_1,x_2,\cdots ,x_{M\times N}\right\}$， $Y_n=\left\{y_1,y_2,\cdots ,y_{M\times N}\right\}$， $Z_n=\left\{z_1,z_2,\cdots ,z_{M\times N}\right\}$， $Q_n=\left\{q_1,q_2,\cdots ,q_{M\times N}\right\}$。

3.2. 加密过程

Step 1. 将伪随机序列 $X_n$ 和 $Z_n$， $Y_n$ 和 $Q_n$ 分别相加，得到两组新的序列 $X{Z}_n$ 和 $Y{Q}_n$ ：

$X{Z}_n=X_n+Z_n$， $Y{Q}_n=Y_n+Q_n$。

Step 2. 使用排序sort函数得到序列 $X{Z}_n$ 和 $Y{Q}_n$ 的两个 $1\times MN$ 的索引序列 $sort\_X{Z}_n$， $sort\_Y{Q}_n$。

Step 3. 将明文图像P按列重排成 $1\times MN$ 的向量，使用索引序列 $sort\_X{Z}_n$ 对其进行位置的置乱后重排成 $M\times N$ 的置乱矩阵 $P_0$。

Step 4. 将置乱矩阵 $P_0$ 按行重排成 $1\times MN$ 的向量，使用索引序列 $sort\_Y{Q}_n$ 对其进行位置的置乱后重排成 $M\times N$ 的置乱矩阵 $P_1$。

Step 5. 将矩阵 $P_1$ 转换为大小为 $M\times 4N$ 的四进制矩阵I，然后将矩阵I分成两个大小为 $M\times 2N$ 的矩阵 $I_1$ 和 $I_2$。

Step 6. 将 $I_2$ 进行元胞自动机演化得到 $F{I}_2$，并与 $I_1$ 异或得到 $R_0$ ： $I_1\oplus F{I}_2=R_0$。

Step 7. 将 $R_0$ 进行元胞自动机演化得到 $F{R}_0$，与 $I_2$ 异或得到 $R_1$ ： $I_2\oplus F{R}_0=R_1$。

Step 8. 将四值矩阵 $R_0$ 和 $R_1$ 左右拼合成一个新的四值矩阵 $R_2$， $R_2$ 矩阵的大小为 $M\times 4N$。

Step 9. 将 $R_2$ 与四值密钥流矩阵FSS异或得到矩阵RR。

Step 10. 将四值矩阵RR转化为十进制的矩阵，得到加密完成的矩阵密文C。

解密方法是加密方法的逆过程，这里不再赘述。过程是可逆的，同样密钥的情况下，可以无失真地恢复解密原始的明文图像。上述加密过程是针对一般灰度图像而写，需要加密彩色RGB图像时，只需要将RGB三个通道分别进行上述步骤的加密即可。

4. 实验结果与性能分析

本文提出的加密算法以及性能分析均在Window10系统中版本为R2016a的Matlab中实现。选用一些经典常用的图像作为加密图像，图5展示了Lena明文图像、密文图像以及解密图像，可以看到明文图像和解密图像完全相同，且密文图像在视觉上不能得到任何与原图像有关的信息。本节将利用经典的安全分析方法来评估本文所提出算法的性能。实验所用的明文图像是大小为512 × 512的Lena图、Living room图、Cameraman图、Baboon图和Pepper图。

(a) (b) (c)

Figure 5. Encryption and decryption results: (a) Plain image of Lena; (b) Cipher image; (c) Decrypted image

图5. 加密解密结果：(a) Lena明文图像；(b) 密文图像；(c) 解密图像

4.1. 性能分析指标UACI和NPCR

为了衡量图像密码系统对抗差分攻击的能力，密码学专家提出了NPCR (Number of Pixels Change Rate)和UACI (Unified Average Changing Intensity)作为两个性能指标(10)：

$NPCR=\frac{{\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}D\left(i,j\right)\times 100\%}}}{M\times N}$, $UACI=\frac{{\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}\left|P_1\left(i,j\right)-P_2\left(i,j\right)\right|\times 100\%}}}{M\times N\times 255}$. (10)

其中 $D\left(i,j\right)=\{\begin{array}{l}0,P_1\left(i,j\right)=P_2\left(i,j\right),\\ 1,P_1\left(i,j\right)\ne P_2\left(i,j\right).\end{array}$ 由公式的定义可知NPCR反映的是两幅图像在相同的位置有多少比

例的像素点完全不同，而UACI反映的是相同位置上像素点的值的平均变化程度。NPCR和UACI是作为衡量明文发生微小差别时进行相同算法的加密后，对密文进行敏感性分析的指标被提出来的，但学者们也经常使用这两个指标来衡量密钥的敏感性。NPCR和UACI的理论期望值分别为99.6094%和33.4635%，这两个指标越接近理论期望值说明加密效果越好，性能更佳。

4.2. 密钥敏感性

密钥敏感性测试意在检测当密钥发生微小的改变时，加密同一幅明文图像得到的两幅图像是否有显著的差异，差异越大说明该算法的密钥敏感性强，抵御蛮力攻击的能力越强。本文实验所用密钥为 $p=0.618$， $a=3.99$， $x=0.345$， $chen\_x_0=1.1$， $chen\_y_0=2.2$， $chen\_z_0=3.3$， $chen\_q_0=4.4$。每次只对其中某一个密钥参数做大小为 ${10}^{-n}$ 的微小扰动，对灰度图大小为512 × 512的Lena图、Living room图、Cameramen图和Baboon图进行加密，测量它们与使用原始的密钥加密后的图像之间的NPCR和UACI值。结果如表2，可以看到密钥微小改变后，计算所得的NPCR和UACI值很接近期望值，说明该算法具有很强的密钥敏感性。在未将元胞自动机的规则号作为密钥考虑情况下，从密钥敏感性结果可以看出，加密算法的密钥空间大小已达到 ${10}^{16\text{+}15\text{+}16\text{+}4\times 14}={10}^{103}$，足够抵御蛮力攻击。

4.3. 明文敏感性

明文敏感性分析(即差分攻击分析)旨在分析使用同一个密钥和加密算法对差别微小的两幅明文图像进行加密得到的两幅密文图像的差别。如果这两幅密文图像差别较小说明该算法一般不能抵御明文攻击。一个良好的算法应该具有较好的明文敏感性。该分析同样使用到了度量NPCR和UACI，这两个值越接近理论值，则明文敏感性效果越好，抵御差分攻击的能力越强。

Table 2. Key sensitivity

表2. 密钥敏感性

本文随机选取明文图像Lena的400个像素点，对这400个像素点每次改变一个像素点1个级别的灰度值，测量400次NPCR和UACI，并取平均值。结果如表3所示，其中小数点后第三、四位为00仅代表对比文献结果只表示到小数点后两位。通过对比，本文所得结果在所有对比文献中最接近理论期望值，说明本文所提出的加密算法具有很好的明文敏感性。

Table 3. Plaintext sensitivity (resistance to differential attacks)

表3. 明文敏感性(抗差分攻击)

4.4. 直方图分析

图像的直方图可以清晰的显示出这副图像的每个灰度值的分布情况。每一幅明文图像均具有其特定的像素分布模式，若加密算法无法将这一特定的分布模式隐藏，破译者可以通过这一特点获得一些跟明文相关的信息从而更容易对加密进行破解。因此，一个好的加密算法不止需要在视觉效果上打乱图像，也需要使得该图像在像素上分布均匀。图6显示了Lena、Livingroom和Baboon的明文图像和密文图像的直方图，可以看到密文图像的直方图中像素值的分布均匀。

(a) (b) (c) (d) (e) (f)

Figure 6. Histogram analysis: (a) Lena’s histogram; (b) Livingroom’s histogram; (c) Baboon’s histogram; (d) Lena cipher image’s histogram; (e) Livingroom cipher image’s histogram; (f) Baboon cipher image’s histogram

图6. 直方图分析：(a) Lena直方图；(b) Livingroom直方图；(c) Baboon直方图；(d) Lena密文图像直方图；(e) Livingroom密文图像直方图；(f) Baboon密文图像直方图

4.5. 相关性测试

相关性测试用来测量图像在水平、垂直、对角上的相邻像素值的相关性。可以知道，相邻像素值的相关性越小，该加密算法的效果越好。计算相关系数的公式见(11)~(12)：

$r_{xy}=\frac{\mathrm{cov}\left(x,y\right)}{\sqrt{D\left(x\right)D\left(y\right)}}$, $\mathrm{cov}\left(x,y\right)=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right)}$, (11)

$D\left(x\right)=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(x_i-E\left(x\right)\right)}^2}$, $E\left(x\right)=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{x}_i}$, (12)

其中x和y表示相邻像素点的像素值， $r_{xy}$ 表示相关系数。

随机选择图像Lena中6000个像素点进行相关性测试，表4显示了明文图像以及其密文图像的相邻像素相关系数以及一些文献结果的对比。图7绘制了明文图像和密文图像的水平、垂直、对角方向的相邻像素值的分布。从密文图像的相邻像素值的相关系数和分布图，可以看到该加密算法大大降低了明文图像的像素值之间的相关性。

Table 4. Correlation coefficient

表4. 相关系数

(a) (b) (c) (d) (c) (d)

Figure 7. Correlation analysis: (a) Lena’s horizontal direction; (b) Lena’s vertical direction; (c) Lena’s diagonal direction; (d) Cipher image’s horizontal direction; (e) Cipher image’s vertical direction; (f) Cipher image’s diagonal direction

图7. 相关性分析：(a) Lena水平方向；(b) Lena垂直方向；(c) Lena对角方向；(d) 密文图像水平方向；(e) 密文图像垂直方向；(f) 密文图像对角方向

4.6. 信息熵

信息熵反映了图像信息的不确定性，一般来说，熵越大不确定性越大，也即信息量越大，此时可视信息越少。信息熵的计算公式见(13)：

$H=-{\displaystyle \underset{i=0}{\overset{L-1}{\sum }}p\left(i\right){\log }_{2}p\left(i\right)}$, (13)

其中L为图像的灰度级， $p\left(i\right)$ 为灰度值i出现的频率。对于一幅完全随机的图像，当 $L=256$ 时信息熵H的理论值为8。表5展示了所选图像在加密后的信息熵，并且与其他算法加密图像的信息熵对比，可以看到本算法加密后的图像信息熵高度接近于8，表明该加密算法具有较强的随机性。通过与一些文献结果比较，可以看出本文的结果在其中更接近理论值。

Table 5. Information entropy

表5. 信息熵

5. 结语

本文对两个混沌系统做了改进，使其生成的序列具有更好的混沌特性，提出了一种新的二维四值CA，并设计了一种基于改进的混沌系统和二维四值CA的混沌加密算法。第一个改进是将PWLCM和Logistic映射复合生成新的混沌系统。经测试，该复合映射所生成的序列具有很好的伪随机性。第二个改进是对超混沌Chen系统所生成的混沌序列做进一步的量化处理，改进后的序列在时间序列时序图，延迟各阶的自相关系数和互相关系数测试上，比改进前的序列均有明显的性能提升。二维四值CA的构造使得传统的二值CA的演化过程更加复杂，结合加权操作使得CA的演化行为变得更加不可预测。最后设计了一个基于四值CA并采用置乱–扩散机制的混沌加密新算法。经过密钥敏感性、明文敏感性、直方图、相邻像素相关性、信息熵等分析，表明本文所提出的图像加密算法具有很强的安全性，在性能上优于比较文献中的图像加密算法。