相对论流体力学方程的高分辨率熵相容格式

High Resolution Entropy Consistent Scheme for Relativistic Hydrodynamics Equations

摘要: 本文提出了一种求解相对论流体力学方程的高分辨率熵相容格式。新格式主要是由熵相容格式以及斜率限制器两个部分构成。首先设计了一个熵相容格式(EC格式)的数值通量。接着为了更好地捕捉到解的结构，建立了一个基于MUSCL (Monotone Upstream-centred Scheme for Conservation Laws)型重建方法的斜率限制器，并将它应用于熵相容格式中，从而得到了高分辨率熵相容格式(EC-Limited格式)。文中还证明了新构造的EC格式和EC-Limited格式的收敛性。在解的光滑区域，EC-Limited格式具有高精度的特性；而在解的间断区域，EC-Limited格式能够恰当地控制耗散，从而抑制非物理现象的发生。最后，对相对论流体力学方程的一维和二维算例进行数值模拟，证明了新格式的稳定性以及良好的性能。

Abstract: A high-resolution entropy consistent scheme was developed for solving the relativistic hydrody-namics equations. The new scheme is composed of entropy consistent scheme and slope limiter. First, an entropy consistent numerical flux (EC scheme) was designed. In order to capture the struc-ture of the solution better, a slope limiter based on MUSCL (Monotone Upstream-centred Scheme for Conservation Laws) type reconstruction method is constructed, the high-resolution entropy con-sistent scheme is obtained by applying it to the entropy consistent scheme. The convergences of the EC scheme and EC-Limited scheme have been proved. For the smooth region of the solution, the EC-Limited scheme has the characteristics of high accuracy, and for the discontinuous region, it can precisely control the dissipation and restrain the occurrence of non-physical phenomena. Finally, several one and two-dimensional numerical experiments demonstrate the stability and good performance of the high-resolution entropy consistent scheme.

1. 引言

相对论流体力学(Relativistic Hydrodynamics, RHD)在现代物理学、高能物理学、核物理学等许多领域发挥着重要作用。由于理想相对论流体力学方程组可以转化为双曲守恒律方程组，因此我们试图将求解双曲守恒律方程的方法推广到理想相对论流体力学方程上，以此寻求更高效、稳定的数值方法。

随着对双曲守恒律方程数值方法的不断研究，人们发现即便初值函数光滑，它的解在某个时刻也可能会出现违背古典解的现象，例如接触间断、激波等。在实际物理问题中，这些间断现象表现为熵增；如何在数值方法中体现熵增现象，一直是学者们持续研究的课题。为了解决上述间断现象带来的问题，1954年，Lax提出了弱解 [1] 的概念，允许间断解存在；但还需要添加一定的条件来得到满足物理意义的惟一的弱解，于是Lax又提出了熵稳定条件 [2]，为研究物理解提供了一种简单有效的途径。Tadmor在1987年提出一类二阶的熵守恒格式 [3]，并指出：一个守恒型三点差分格式，只要含有比熵守恒格式更多的数值粘性，则该三点守恒型格式就是熵稳定的。这一结论为我们构造熵稳定格式提供了理论保证。2006年，Roe在熵守恒格式基础上添加数值粘性项，得到一类熵稳定格式 [4]，称为ERoe格式。紧接着在2009年，Roe、Ismail两人对熵增进行深入的分析后，得到了对数值粘性项更精确量化的熵相容格式 [5]。近些年来，国内的郑素佩等 [6] 将熵稳定格式和HLL格式结合，得到求解二维浅水波方程的高分辨率旋转混合通量格式；封建湖教授也在熵稳定/熵相容格式方面做了大量的研究 [7] [8] [9]，同时将格式推广到各种双曲守恒律方程中，并借助限制器、WENO重构等方法进一步控制激波处的熵增，使数值结果更加准确。

近四十年来，随着对RHD方程逐渐深入的研究，其数值求解方法得到了飞快的发展。在国内，汤华中教授也持续关注着RHD方程，构造了一系列行之有效的格式 [10] [11] [12] [13]。2021年，任璇提出了一种求解双曲守恒律方程的熵相容格式 [14]，本文将此格式推广应用到RHD方程上，并引入基于MUSCL型重构方法的斜率限制器，使之与熵相容格式结合，进而提高数值方法的精度，得到高分辨率熵相容格式，并给出若干个数值算例检验其可行性。

2. 相对论流体力学方程

一维RHD方程的守恒律形式如下

$U_t+F{\left(U\right)}_x=0,$ (1)

其中，守恒型变量和通量分别为

$U={\left[D,m,E\right]}^{\text{T}},F\left(U\right)={\left[Du,mu+p,m\right]}^{\text{T}}.$ (2)

其中质量密度，动量密度，能量密度分别为

$D=\rho W,m=DhWu,E=DhW-p.$ (3)

公式(2)和(3)中 $\rho$ 表示物质的固有密度，p表示压力，u是归一化(取光速 $c=1$ )的流体速度； $W=\frac{1}{\sqrt{1-u^2}}$ 表示Lorentz因子， $h=1+e+\frac{p}{\rho }$ 表示比焓，e是比内能。对于理想气体，可添加状态方程

$p=\left(\gamma -1\right)\rho e.$ (4)

使方程(1)封闭，其中 $\gamma \in \left(1,2\right]$ 是绝热指数。

方程(1)的雅可比矩阵为 [15]

$A=\frac{\partial F\left(U\right)}{\partial U}=\frac{1}{N}\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ 0& A_{32}& 0\end{array}\right).$

其中 $A_{11}=\frac{u^{2}h\left(1-c_s^2\right)}{\gamma -1}+\frac{uh}{W^2}$， $A_{12}=-\frac{1}{W^3}+\frac{\gamma }{W\left(\gamma -1\right)}$， $A_{13}=-\frac{u\gamma }{W\left(\gamma -1\right)}$， $A_{21}=-\frac{h^2}{W^3}\left(1-\frac{c_s^2}{\gamma -1}\right)$， $A_{22}=-\frac{uh}{W^2}\left(1-\frac{c_s^2}{\gamma -1}\right)+\frac{2uh\left(1-c_s^2\right)}{\gamma -1}$， $A_{23}=-\frac{u^{2}h\left(1-c_s^2\right)}{\gamma -1}+\frac{h}{W^2}$， $A_{32}=\frac{h\left(1-c_s^2{u}^2\right)}{\gamma -1}$， $N=\frac{h\left(1-c_s^2{u}^2\right)}{\gamma -1}$。

雅可比矩阵的特征值为 ${\lambda }_{-}=\frac{u-c_s}{1-u{c}_s}$， ${\lambda }_0=u$， ${\lambda }_{+}=\frac{u+c_s}{1+u{c}_s}$。

式中的 $c_s=\sqrt{\left(\gamma p\right)/\left(\rho h\right)}$ 表示为声速，h是比焓。雅可比矩阵的特征值所对应的右特征向量矩阵为 [13]

$R=\left(\begin{array}{ccc}1& 1& 1\\ \left(u-c_s\right)Wh& uW& \left(u+c_s\right)Wh\\ \left(1-u{c}_s\right)Wh& W& \left(1+u{c}_s\right)Wh\end{array}\right)\left(\begin{array}{ccc}\sqrt{\frac{\rho W\left(1-u{c}_s\right)}{2\gamma }}& 0& 0\\ 0& \sqrt{\frac{\left(\gamma -1\right)\rho W}{\gamma }}& 0\\ 0& 0& \sqrt{\frac{\rho W\left(1+u{c}_s\right)}{2\gamma }}\end{array}\right).$

方程(1)的雅可比矩阵特征值皆是实数，且其对应的特征向量线性无关，由此可知，方程(1)是双曲型方程组。故本文可将求解双曲守恒律方程的一系列数值方法推广应用到相对论流体力学方程上。

因为Lorentz因子的存在，守恒型变量不能直接转变为原始变量，致使方程的数值求解方法更加繁琐复杂。由表达式(3)、(4)、以及 $h=1+e+p/\rho$，有

$\begin{array}{c}E+p=DhW=DW\left(1+e+\frac{p}{\rho }\right)=DW+DW\left(e+\frac{p}{\rho }\right)=DW+DW\left(\frac{1}{\gamma -1}\frac{p}{\rho }+\frac{p}{\rho }\right)\\ =DW+\frac{\gamma }{\gamma -1}DW\frac{p}{\rho }=DW+\frac{\gamma }{\gamma -1}p{W}^2,\end{array}$ (5)

其中 $W={\left(1-m^2/{\left(E+p\right)}^2\right)}^{-\frac{1}{2}}$。为了恢复原始变量 $\left(\rho ,u,p\right)$ 的值，需对式(5)进行求解。此时方程(5)变为关于变量p的非线性方程，在已知守恒型变量 $U=\left(D,m,E\right)$ 的数值时，利用牛顿迭代法求解压力p，然后根据关系式 $\rho =D/W$， $h=1+\left(\gamma p/\left(\left(\gamma -1\right)\rho \right)\right)$， $u=m/\left(DhW\right)$，求出密度 $\rho$ 和速度u。

为构造RHD方程的熵相容格式，定义其熵函数 $M\left(U\right)=-\frac{\rho WS}{\gamma -1}$，熵通量函数 $N\left(U\right)=-\frac{\rho uWS}{\gamma -1}$，其中热力学熵 $S=\ln \left(p\right)-\gamma \ln \left(\rho \right)$，对应的熵变量为：

$V={\left[\frac{\gamma -S}{\gamma -1}+\frac{\rho }{p},\frac{\rho Wu}{p},-\frac{\rho W}{p}\right]}^{\text{T}}.$ (6)

本文采用空间半离散守恒型格式

$\frac{\text{d}}{\text{d}t}{U}_i\left(t\right)=-\frac{1}{\Delta x}\left(F_{i+1/2}-F_{i-1/2}\right).$ (7)

时间方向采用三阶龙格库塔方法 [16]

$\{\begin{array}{l}{U}^{*}=U^n+\Delta tL\left(U^n\right),\hfill \\ U^{**}=\frac{3}{4}{U}^n+\frac{1}{4}{U}^{*}+\frac{\Delta t}{4}L\left(U^{**}\right),\hfill \\ U^{n+1}=\frac{1}{3}{U}^n+\frac{2}{3}{U}^{**}+\frac{\Delta t}{4}L\left(U^{**}\right).\hfill \end{array}$ (8)

其中 $L\left(U\right)=-\frac{1}{\Delta x}\left(F_{i+1/2}-F_{i-1/2}\right)$。

3. 熵相容格式

3.1. 熵守恒格式

在保持总熵不变，且在离散情况下满足如下熵等式的格式称之为熵守恒格式：

$\frac{\text{d}}{\text{d}t}M\left(U_i\left(t\right)\right)+\frac{1}{\Delta x}\left(N_{i+1/2}-N_{i-1/2}\right)=0，$ (9)

其中M为熵函数， $N_{i+1/2}$ 为数值熵通量函数 [2]，且 $N_{i+1/2}$ 与熵通量函数N相容。

2019年，Tang [13] 提出了求解RHD方程的熵守恒格式。引入参数向量 $z={\left(z_1,z_2,z_3\right)}^{\text{T}}={\left(\rho ,\rho /p,u\right)}^{\text{T}}$，熵守恒通量为 $F^C={\left(F_1,F_2,F_3\right)}^{\text{T}}$，其中

$\{\begin{array}{l}{F}_1=z_1^{\ln }\overline{\left(uW\right)},\hfill \\ F_2=B^{-1}\left[\left(1+\frac{1}{\left(\gamma -1\right)z_2^{\ln }}\right)\overline{z_2}{z}_3^{Lor}{F}_1+\overline{z_1}{\bar{W}}^2+\overline{z_1}\overline{z_3}\bar{W}{z}_3^{Lor}\right],\hfill \\ F_3=B^{-1}\left[\overline{z_1}\bar{W}\overline{\left(uW\right)}+\overline{z_1}\overline{z_3}\overline{\left(uW\right)}{z}_3^{Lor}+\left(1+\frac{1}{\left(\gamma -1\right)z_2^{\ln }}\right)F_1\left(\overline{z_2}\bar{W}+\overline{z_2}\overline{z_3}{z}_3^{Lor}\right)\right].\hfill \end{array}$ (10)

公式(10)中 $B=\overline{z_2}{\bar{W}}^2+\overline{z_2}\overline{z_3}\bar{W}{z}_3^{Lor}-\overline{z_2}\overline{\left(uW\right)}{z}_3^{Lor}$ ； $\overline{z_{i+1/2}}=\frac{z_i+z_{i+1}}{2}$ ； $\overline{\left(uW\right)}$ 表示u和W的乘积取平均值； ${(\cdot )}^{\ln }$ 是对数平均 [5]； $z_3^{Lor}$ 是Lorentz平均，且

$z_3^{Lor}=u^{Lor}=\frac{u_i+u_{i+1}}{\sqrt{1-u_i^2}\sqrt{1-u_{i+1}^2}\left(\sqrt{1-u_i^2}+\sqrt{1-u_{i+1}^2}\right)}.$ (11)

3.2. 熵稳定格式

熵守恒格式是保持总熵不变的，因而该格式在解的连续区域有着良好的性能，但在解的间断处会出现伪振荡现象。为了使格式更好地捕捉到解的结构，就需要总熵有一定的耗散。Tadmor [3] 指出：在熵守恒格式基础上，添加更多数值粘性，且满足如下离散熵不等式的三点格式为熵稳定格式。

$\frac{\text{d}}{\text{d}t}M\left(U_i\left(t\right)\right)+\frac{1}{\Delta x}\left(N_{i+1/2}-N_{i-1/2}\right)<0.$ (12)

本文将Roe格式的数值粘性项 [4] 添加到熵守恒格式数值通量(10)中，熵稳定格式数值通量为

$F^{ES}=F^C-\frac{1}{2}R\left|\Lambda \right|R^{-1}\left[U\right].$

1999年，Barth [17] 证明了 $U_V\approx R{R}^{\text{T}}$，故有

$\frac{1}{2}R\left|\Lambda \right|R^{-1}\left[U\right]\approx \frac{1}{2}R\left|\Lambda \right|R^{-1}{U}_V\left[V\right]=\frac{1}{2}R\left|\Lambda \right|R^{-1}R{R}^{\text{T}}\left[V\right]=\frac{1}{2}R\left|\Lambda \right|R^{\text{T}}\left[V\right].$ (13)

从而得到求解RHD方程的熵稳定格式数值通量为

$F^{ES}=F^C-\frac{1}{2}R\left|\Lambda \right|R^{\text{T}}\left[V\right],$ (14)

式中， $F^C$ 的表达式为公式(10)， $\Lambda =\text{diag}\left(\frac{\bar{u}-\overline{c_s}}{1-\bar{u}\overline{c_s}},\bar{u},\frac{\bar{u}+\overline{c_s}}{1+\bar{u}\overline{c_s}}\right)$， $R$ 是对应的右特征向量构成的矩阵。

3.3. 熵相容格式

熵稳定格式比熵守恒格式含有更多的数值粘性，但仍然不能避免出现伪振荡现象。Roe、Ismail [5] 给出了求解双曲守恒律方程的熵相容格式，并推广应用到Euler方程上。本文将文献 [14] 中的熵相容格式的表达式推广应用到相对论流体力学方程中，数值通量为

$F^{EC}=F^C-\frac{1}{2}{\left(\tilde{Q}\right)}^{+}\left[U\right]-\frac{1}{2}R\left|\Lambda \right|R^{-1}\left[U\right],$

其中， $F^C$ 的表达式为(10)， $\tilde{Q}=\frac{1}{6}\left(R_R\left|{\Lambda }_R\right|R_R^{-1}-R_L\left|{\Lambda }_L\right|R_L^{-1}\right)$， ${\left(\tilde{Q}\right)}^{+}=R_Q{\left({\Lambda }_Q\right)}^{+}{R}_Q^{-1}$。

利用关系式(13)，文献 [14] 给出了熵相容格式的另一种表示，将上式的数值粘性项写为熵变量的差分形式，从而得到求解RHD方程的熵相容格式，其数值通量为

$F^{EC}=F^C-\frac{1}{2}{\left(Q\right)}^{+}\left[V\right]-\frac{1}{2}R\left|\Lambda \right|R^{\text{T}}\left[V\right],$ (15)

其中， $Q=\frac{1}{6}\left(R_R\left|{\Lambda }_R\right|R_R^{\text{T}}-R_L\left|{\Lambda }_L\right|R_L^{\text{T}}\right)$， ${\left(Q\right)}^{+}=R_Q{\left({\Lambda }_Q\right)}^{+}{R}_Q^{\text{T}}$，下标 $L,R$ 分别表示用于计算特征值 $\Lambda$ 和特征向量 $R$ 中的变量的左、右状态， ${\Lambda }_Q$ 是矩阵 $Q$ 的特征值矩阵， $R_Q$ 是对应的右特征向量矩阵， ${\left({\Lambda }_Q\right)}^{+}$ 表示 ${\Lambda }_Q$ 中的负数替换为0，其余数值不变的矩阵 [18]。

$\left|\Lambda \right|$ 的取法在Roe格式和Lax-Friedrichs格式两种类型中任取其一即可。

$\left|\Lambda \right|=\{\begin{array}{l}\text{diag}\left(\left|{\lambda }_1\right|,\cdots ,\left|{\lambda }_n\right|\right),\text{Roescheme},\hfill \\ \max \left(\left|{\lambda }_1\right|,\cdots ,\left|{\lambda }_n\right|\right)I,\text{Lax-Friedrichsscheme,}\hfill \end{array}$

其中 $I$ 是单位矩阵， ${\lambda }_1,\cdots ,{\lambda }_n$ 是雅可比矩阵 $A$ 的特征值。

在离散情况下，RHD方程的熵相容格式的数值通量表达式为

$F_{i+1/2}^{EC}=F_{i+1/2}^C-\frac{1}{2}{\left(Q_{i+1/2}\right)}^{+}{\left[V\right]}_{i+1/2}-\frac{1}{2}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2},$ (16)

式(16)中 ${\Lambda }_{i+1/2}=\text{diag}\left(\frac{\overline{u_{i+1/2}}-\overline{{\left(c_s\right)}_{i+1/2}}}{1-\overline{u_{i+1/2}}\overline{{\left(c_s\right)}_{i+1/2}}},\overline{u_{i+1/2}},\frac{\overline{u_{i+1/2}}+\overline{{\left(c_s\right)}_{i+1/2}}}{1+\overline{u_{i+1/2}}\overline{{\left(c_s\right)}_{i+1/2}}}\right)$， $R_{i+1/2}$ 则是对应的右特征向量构成的矩阵， $c_s=\sqrt{\left(\gamma p\right)/\left(\rho h\right)}$ 为音速， $\overline{{\left(c_s\right)}_{i+1/2}}={\left(\gamma \overline{p_{i+1/2}}/\left(\overline{{\rho }_{i+1/2}}\overline{h_{i+1/2}}\right)\right)}^{1/2}$， $\overline{{\rho }_{i+1/2}}={\rho }_{i+1/2}^{\ln }$， ${\left[V\right]}_{i+1/2}=V_{i+1}-V_i$， $\overline{p_{i+1/2}}={\rho }_{i+1/2}^{\ln }/{\left(p/\rho \right)}_{i+1/2}^{\ln }$， $\overline{h_{i+1/2}}=1+\frac{\gamma }{\gamma -1}\frac{\overline{p_{i+1/2}}}{{\rho }_{i+1/2}}$。

引理 [3] 若与 $F$ 相容的数值通量函数 $F_{i+1/2}=\left(U_i,U_{i+1}\right)$ 关于 $U_i,U_{i+1}$ 是Lipschitz连续的，那么存在一个数值粘性矩阵 $G_{i+1/2}$ 使得 $F_{i+1/2}$ 可以写成带数值粘性的形式

$F_{i+1/2}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}\left(U_{i+1}-U_i\right).$

定理1数值通量为(16)的熵相容格式(EC)是收敛的。

证明：上述提到的熵守恒格式与熵相容格式均为守恒型三点差分格式，将熵相容格式的数值通量 $F_{i+1/2}^{EC}$ 写成带数值粘性的形式

$F_{i+1/2}^{EC}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{\tilde{G}}_{i+1/2}^{EC}{\left[U\right]}_{i+1/2},$

其中 ${\tilde{G}}_{i+1/2}^{EC}=G_{i+1/2}^C+{\left({\tilde{Q}}_{i+1/2}\right)}^{+}+R_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{-1}$， $G_{i+1/2}^C$ 是熵守恒格式对应的数值粘性矩阵。

从关系式(13)可知，熵相容格式的数值通量 $F_{i+1/2}^{EC}$ 可写成带数值粘性的形式

$F_{i+1/2}^{EC}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2},$

其中 $G_{i+1/2}^{EC}=G_{i+1/2}^C+{\left(Q_{i+1/2}\right)}^{+}+R_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}$，令 $P_{i+1/2}^{EC}=G_{i+1/2}^{EC}-G_{i+1/2}^C={\left(Q_{i+1/2}\right)}^{+}+R_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}$，则

$\begin{array}{c}{\left[V\right]}_{i+1/2}^{\text{T}}{P}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}={\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}-{\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^C{\left[V\right]}_{i+1/2}\\ ={\left[V\right]}_{i+1/2}^{\text{T}}{\left(Q_{i+1/2}\right)}^{+}{\left[V\right]}_{i+1/2}+{\left[V\right]}_{i+1/2}^{\text{T}}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}\\ ={\left[V\right]}_{i+1/2}^{\text{T}}{\left(Q_{i+1/2}\right)}^{+}{\left[V\right]}_{i+1/2}+{\left(R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}\right)}^{\text{T}}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}.\end{array}$

由于 ${\left(Q_{i+1/2}\right)}^{+}$ 是半正定矩阵， $\left|{\Lambda }_{i+1/2}\right|$ 是正定矩阵， $R_{i+1/2}^{\text{T}}$ 是可逆矩阵， ${\left[V\right]}_{i+1/2}$ 为非零向量，从而 $R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}$ 是非零向量，有 ${\left(R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}\right)}^{\text{T}}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[V\right]}_{i+1/2}>0$， ${\left[V\right]}_{i+1/2}^{\text{T}}{\left(Q_{i+1/2}\right)}^{+}{\left[V\right]}_{i+1/2}\ge 0$，故 ${\left[V\right]}_{i+1/2}^{\text{T}}{P}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}>0$，说明熵相容格式比熵守恒格式具有更多的数值粘性，由Tadmor的比较原则 [3] 知，熵相容格式是满足熵稳定条件的，其数值解是收敛的。

4. 高分辨率熵相容格式

4.1. 斜率限制器

在每个控制单元 $I_i=\left[x_{i-1/2},x_{i+1/2}\right]$ 上，将双曲守恒律方程的精确解 $u\left(x\right)$ 表示为分段的精确解 $u_i\left(x\right)$，我们对 $u_i\left(x\right)$ 进行重构，重构之后的函数表示为 $R_i\left(x\right)$。如果有 $\left|u_i\left(x\right)-R_i\left(x\right)\right|\le {\rm O}\left({\left(\Delta x\right)}^{k+1}\right)$ 成立，则称重构函数 $R_i\left(x\right)$ 具有k阶精度。 $u_i^n$ 表示在时间层 $t^n$ 上单元 $I_i$ 的平均值，有如下表达式：

$u_i^n=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{R}_i\left(x\right)\text{d}x}=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{u}_i\left(x\right)\text{d}x}.$

将 $R_i\left(x\right)$ 在 $x_i$ 点处泰勒展开，得

$R_i\left(x\right)=u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\frac{{\left(x-x_i\right)}^2}{2}+\cdots ,$ (17)

同样地将 $u_i\left(x\right)$ 在 $x_i$ 点处泰勒展开，得

$\begin{array}{c}{\displaystyle {\int }_{I_i}{u}_i\left(x\right)\text{d}x}=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}\left(u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\frac{{\left(x-x_i\right)}^2}{2}+\cdots \right)\text{d}x}\\ =u_i\left(x_i\right)+0+\frac{1}{\Delta x}{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}{\displaystyle {\int }_{I_i}\frac{{\left(x-x_i\right)}^2}{2}\text{d}x}+\cdots ,\end{array}$ (18)

联合式(17) (18)，得到 $R_i\left(x\right)=u_i^n+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+\frac{1}{2}{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left({\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right)+\cdots$

为方便后续运算，将 $R_i\left(x\right)$ 的表达式记为

$R_i\left(x\right)=u_i^n+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+\frac{1}{2}{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left({\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right).$ (19)

若其满足不等式 $R_i\left(x\right)=u_i^n+H\left(x-x_i\right)$，其中

$H\left(x-x_i\right)={\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+\frac{1}{2}{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left({\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right).$

本文采用中心差商对一阶、二阶偏导数进行处理，即

${\frac{\partial u_i}{\partial x}|}_{x_i}=\frac{u_{i+1}^n-u_{i-1}^n}{2\Delta x},{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}=\frac{u_{i+1}^n-2u_i^n+u_{i-1}^n}{\Delta x^2}.$

将高精度重构式进行限制，有 $R_i\left(x\right)=u_i^n+{\phi }_{i}H\left(x-x_i\right)$， ${\phi }_i\in \left[0,1\right]$ 是一个斜率限制器。

$R_i\left(x\right)$ 在每个控制单元 $I_i=\left[x_{i-1/2},x_{i+1/2}\right]$ 的左右边界外推值分别为

$R_i^L\left(x\right)=u_i^n+{\phi }_{i}H\left(x_{i-1/2}-x_i\right),R_i^R\left(x\right)=u_i^n+{\phi }_{i}H\left(x_{i+1/2}-x_i\right).$

为保证不会产生新的局部极值，这二者需满足下列不等式：

$\{\begin{array}{c}\min \left(u_{i-1}^n,u_i^n\right)\le R_i^L\le \max \left(u_{i-1}^n,u_i^n\right),\\ \min \left(u_{i+1}^n,u_i^n\right)\le R_i^R\le \max \left(u_{i+1}^n,u_i^n\right).\end{array}$

上式中不等式两边同时减去 $u_i^n$ 得到

$\{\begin{array}{c}\min \left(u_{i-1}^n-u_i^n,0\right)\le R_i^L\le \min \left(u_{i-1}^n-u_i^n,0\right),\\ \min \left(u_{i+1}^n-u_i^n,0\right)\le R_i^R\le \min \left(u_{i+1}^n-u_i^n,0\right).\end{array}$

以第一个不等式为示例来分析数据左状态的重构过程。

当 $u_{i-1}^n>u_i^n$ 时，不等式变为 $0\le R_i^L-u_i^n\le u_{i-1}^n-u_i^n$，即 $0\le {\phi }_{i}H\left(x_L-x_i\right)\le u_{i-1}^n-u_i^n$，由于 ${\phi }_i\in \left[0,1\right]$，选左边的斜率限制器为 ${\phi }_L=\min \left(1,\frac{u_{i-1}^n-u_i^n}{H\left(x_L-x_i\right)}\right)$ ；当 $u_{i-1}^n<u_i^n$ 时，选取同样的左斜率限制器；当 $u_{i-1}^n=u_i^n$ 时，解充分的光滑，故取 ${\phi }_L=0$。与上述过程相同，右边的斜率限制器为 ${\phi }_R=\min \left(1,\frac{u_{i+1}^n-u_i^n}{H\left(x_R-x_i\right)}\right)$。

为保证上述不等式成立，对斜率限制器进行修正：

$\{\begin{array}{c}{\phi }_L=\min \left(1,\frac{u_{i-1}^n-u_i^n}{H\left(x_L-x_i\right)}\right),\\ {\phi }_R=\min \left(1,\frac{u_{i+1}^n-u_i^n}{H\left(x_R-x_i\right)}\right),\\ {\phi }_i=\max \left(\min \left({\phi }_L,{\phi }_R\right),0\right).\end{array}$ (20)

4.2. 高分辨率熵相容格式

在熵相容格式数值通量(公式(16))的基础上，将上一节中提出的斜率限制器(公式(20))应用到该格式中，继而得到高分辨率熵相容格式，其数值通量为

$F_{i+1/2}^{EC-Limited}=F_{i+1/2}^C-\frac{1}{2}{\left(Q_{i+1/2}\right)}^{+}{\left[V^{Limited}\right]}_{i+1/2}-\frac{1}{2}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[V^{Limited}\right]}_{i+1/2},$ (21)

其中 $V^{Limited}$ 是重构后的熵变量值。

在实际重构中，首先用牛顿迭代法求解非线性方程(公式(5))中的p，进而利用公式(3)的关系式，将守恒型变量U变为原始变量，即

$\left[\rho W,\rho h{W}^{2}u,\rho hW-p\right]\to \left[\rho ,u,p\right]$

其次利用上一小节中的数据重构，完成对原始变量的重构，再计算出相应的熵变量 $V^{Limited}$，之后将变量值带入公式(21)中求解对应的数值通量。

定理2数值通量为(21)的高分辨率熵相容格式(EC-Limited格式)是收敛的。

证明：EC格式的数值通量 $F_{i+1/2}^{EC}$ 写成带数值粘性的形式

$\begin{array}{c}{F}_{i+1/2}^{EC}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}\\ =\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}^C{\left[V\right]}_{i+1/2}-\frac{1}{2}{P}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2},\end{array}$

其中 $P_{i+1/2}^{EC}=G_{i+1/2}^{EC}-G_{i+1/2}^C={\left(Q_{i+1/2}\right)}^{+}+R_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}$。

设高分辨率熵相容格式的数值通量 $F_{i+1/2}^{EC-Limited}$ 具有粘性形式

$F_{i+1/2}^{EC-Limited}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}^{EC-Limited}{\left[V\right]}_{i+1/2},$

另将(21)写为带数值粘性的形式

$F_{i+1/2}^{EC-Limited}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}{G}_{i+1/2}^C{\left[V\right]}_{i+1/2}-\frac{1}{2}{P}_{i+1/2}^{EC}{\left[V^{Limited}\right]}_{i+1/2}.$

由上述重构条件可知， $\text{sign}\left({\left[V\right]}_{i+1/2}\right)=\text{sign}\left({\left[V^{Limited}\right]}_{i+1/2}\right)$ 且 $0<\left|{\left[V^{Limited}\right]}_{i+1/2}\right|\le \left|{\left[V\right]}_{i+1/2}\right|$。

设 ${\left[V^{Limited}\right]}_{i+1/2}=k{\left[V\right]}_{i+1/2},k\in \left(0,1\right]$，得

$F_{i+1/2}^{EC-Limited}=\frac{1}{2}\left(F\left(U_i\right)+F\left(U_{i+1}\right)\right)-\frac{1}{2}\left(G_{i+1/2}^C+k{P}_{i+1/2}^{EC}\right){\left[V\right]}_{i+1/2},$

即 $G_{i+1/2}^{EC-Limited}=G_{i+1/2}^C+k{P}_{i+1/2}^{EC}$，故

${\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^{EC-Limited}{\left[V\right]}_{i+1/2}={\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^C{\left[V\right]}_{i+1/2}+k{\left[V\right]}_{i+1/2}^{\text{T}}{P}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2},$

由定理1可知 ${\left[V\right]}_{i+1/2}^{\text{T}}{P}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}>0$，因此

${\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^C{\left[V\right]}_{i+1/2}<{\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^{EC-Limited}{\left[V\right]}_{i+1/2}\le {\left[V\right]}_{i+1/2}^{\text{T}}{G}_{i+1/2}^{EC}{\left[V\right]}_{i+1/2}.$

说明EC-Limited格式的数值粘性介于熵守恒格式和熵相容格式之间，满足熵稳定条件，数值解是收敛的。

5. 数值算例

以下黎曼问题中，边界条件为Neumann边界条件，条件数 $CFL=0.4$，绝热系数 $\gamma =5/3$，熵稳定格式(ES，数值通量为公式(14))、熵相容格式(EC，数值通量为公式(16))与高分辨率熵相容格式(EC-Limited，数值通量为公式(21))均采用400网格点计算，参考解则是由文献 [19] 中的高分辨率熵相容格式使用4000个网格点计算而得。

算例1在区域 $[0,1]$ 上考虑一维相对论流体力学方程的如下初值问题

$\rho \left(x,0\right)=1+0.2\sin \left(2\pi x\right),u\left(x,0\right)=0.2,p\left(x,0\right)=1.$

在计算时采用周期性边界条件，取 $CFL=0.4$，绝热系数 $\gamma =5/3$，计算到 $t=2$ 时刻。该算例的精确解为

$\rho \left(x,t\right)=1+0.2\sin \left(2\pi \left(x-ut\right)\right),u\left(x,t\right)=0.2,p\left(x,t\right)=1.$

表1显示出了不同网格数下密度 $\rho$ 的数值误差以及收敛阶。从表1显示的结果来看，新格式(EC-Limited格式)是具有高精度的特性的，该格式在 $L^1$ 和 $L^2$ 范数意义下收敛阶均超过二阶，在 $L^{\infty }$ 范数意义下收敛阶接近于二阶，与前文所述的理论结果基本一致。

Table 1. Numerical errors and orders of density ρ

表1. 密度 $\rho$ 的数值误差和收敛阶

算例2在区域 $\left[0,1\right]$ 上求解如下初值问题

$\left(\rho ,u,p\right)=\{\begin{array}{l}\left(1,-0.7,20\right),x<0.5\hfill \\ \left(1,0.7,20\right),x>0.5\hfill \end{array}$

该算例的解由两个反方向的稀疏波组成。计算结果见图1。从图1能够观察到，三个格式中，EC-Limited格式的结果与参考解吻合得最好，很好地捕捉到了稀疏波的结构；而在 $x=0.5$ 附近，密度发生了“undershoot”现象，这一现象在非相对论的黎曼问题中同样会发生。同样，在 $x=0.5$ 附近，三个方法中，EC-Limited格式吻合效果最好，ES格式表现最差。

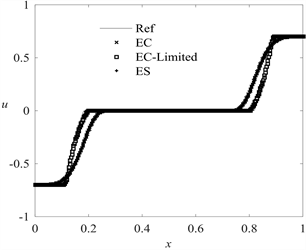
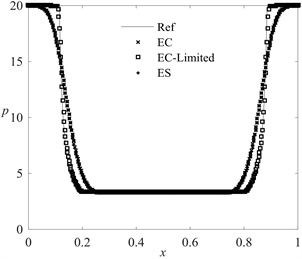
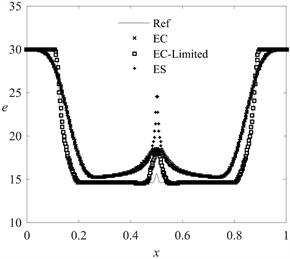
Figure 1. Numerical results of example 2

图1. 算例2的数值结果

算例3在区域 $\left[0,1\right]$ 上求解如下初值问题

$\left(\rho ,u,p\right)=\{\begin{array}{ll}\left(5,0,50\right),\hfill & x<0.5\hfill \\ \left(2+0.3\sin \left(50x\right),0,5\right),\hfill & x>0.5\hfill \end{array}$

图2给出了 $t=0.35$ 时刻的数值解与参考解。从图2中看出激波与正弦波相互作用时，产生了光滑但较为复杂的结构，EC、ES格式不能够准确捕捉到扰动波的峰值，而EC-Limited格式不仅能够锐利地捕捉分辨出激波与稀疏波，还可以很好地捕捉到小幅度的扰动波，而且总熵耗散较小，既有效地抑制了解在大梯度变化区域的抹平现象，也很好地波捉到解的各种详细结构。这充分表明EC-Limited格式的数值粘性大小更为合适，对应的数值熵耗散控制更为精准。

算例4在区域 $\left[0,1\right]\times \left[0,1\right]$ 上求解如下初值问题

$\left(\rho ,u,v,p\right)=\{\begin{array}{ll}\left(0.5,0.5,-0.5,5\right),\hfill & x>0.5,y>0.5\hfill \\ \left(1,0.5,0.5,5\right),\hfill & x<0.5,y>0.5\hfill \\ \left(3,-0.5,0.5,5\right),\hfill & x<0.5,y<0.5\hfill \\ \left(1.5,-0.5,-0.5,5\right),\hfill & x>0.5,y<0.5\hfill \end{array}$

图3、图4展示了ES格式、EC-Limited格式计算至 $t=0.4$ 时刻，单元数目为300 × 300的30条密度对数 $\ln \rho$ 等值线和压力对数 $\ln p$ 等值线。随着时间的不断推进，初始时刻的接触间断在区域中央逐渐形成了一个低密度漩涡。与ES格式相比，EC-Limited格式对解的捕捉更精细，漩涡边界更加清晰，提高了解的分辨率。

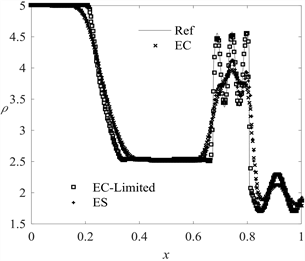
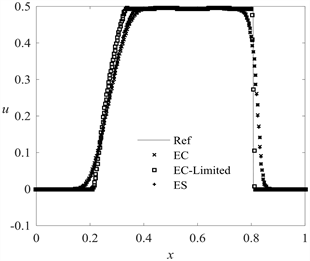
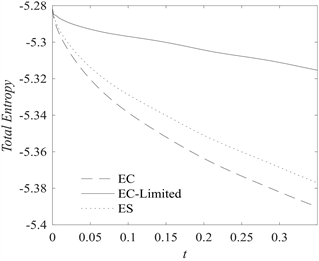
Figure 2. Numerical results of example 3

图2. 算例3的数值结果

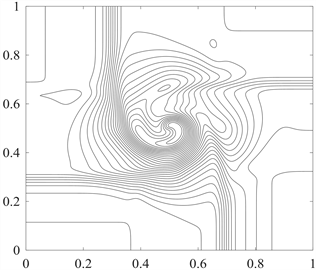
Figure 3. The contours of the density logarithm for example 4: ES scheme (left) and EC-Limited scheme (right)

图3. 算例4的密度对数等值线图：ES格式(左)与EC-Limited格式(右)

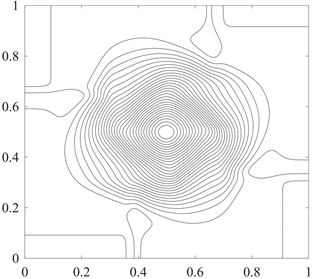
Figure 4. The contours of the pressure logarithm for example 4: ES scheme (left) and EC-Limited scheme (right)

图4. 算例4的压力对数等值线图：ES格式(左)与EC-Limited格式(右)

6. 结论

本文构造了相对论流体力学方程的高分辨率熵相容格式。首先，将双曲守恒律方程的数值方法应用于RHD方程上，接着借助MUSCL型的斜率限制器，将它与熵相容格式结合，得到高分辨率熵相容格式。文中还证明了新构造的熵相容格式(EC格式)和高分辨率熵相容格式(EC-Limited格式)的收敛性。若干个算例的结果均表明，新构造的格式有着高精度高分辨率的特性，其对稀疏波以及激波的逼近效果要优于一般的熵相容格式，是求解RHD方程较好的方法之一。

基金项目

国家自然科学基金(11971075)。

NOTES

^*通讯作者。