1. 引言
国外某公司(如荷兰的Kenz-Figee B. V.公司)有设计和制造各种起重机百来年的历史,其中双纽线型起重机即为其独创 [1] [2]。该型双纽线型起重机安装在浮船上,能够完成水上的过驳、转载等作业;早期的设计为后摇杆驱动,最近又开发了臂架驱动的型式,并已经申请专利 [2]。
逆向工程或称反求设计 [3] [4] 是指对已有的产品或技术进行分析研究,掌握其功能原理、结构、关键技术等指标,在根据现代设计理论与方法技术,对原产品进行仿制、改进设计或创新设计的过程;而对技术图样、专利文献等的逆向工程分析,则对科技人员的要求更高、分析的困难更大。
针对专利产品,运用机构学和逆向工程原理来分析该双纽线型(臂架驱动)变幅机构的速度瞬心、运动轨迹和变幅力矩。双纽线型(臂架驱动)变幅机构独具特点:臂架活动范围大、外观和几何形态特殊,重心高度低等,改善了后摇杆的受力状况。本文旨在利用解析方法来探究和分析该变幅机构的变幅特性,为设计和开发新型起重机打下基础,进而可推广到其它机械产品的设计(如机器人工作机构选型)。
2. 双纽线型变幅机构运动学分析
该双纽线型变幅机构的最大特点是臂架和后摇杆的活动范围很大,单独设有自重平衡系统,由特殊装置驱动、实现水平平衡变幅作业 [3] - [9]。图1所示为该双纽线型变幅机构正在作业的情形。

Figure 1. Photo of lemniscate luffing mechanism (with boom driving)
图1. 正在作业的双纽线型变幅机构(臂架驱动)
2.1. 速度瞬心P求解
双纽线型变幅机构的速度瞬心位置变化很大,随变幅半径的变化:瞬心有时在水平线的上方、有时又出现在水平线的下方。图2所示为该变幅机构的运动简图。
 X1——臂架(主动件);X2——象鼻架后臂;X3——后摇杆;X4——象鼻架前臂;X5——后摇杆下铰点O3与臂架下铰点O1之水平距离;X6——后摇杆下铰点O3与臂架下铰点O1之铅垂距离;X7——象鼻架的下沉量;X8——回转中心线与臂架下铰点O1之水平距离;R——幅度;γ——臂架与象鼻架后臂之夹角;θ1——臂架与水平线之夹角(自变量);θ3——后摇杆与水平线之夹角;β——A点速度向量与水平线之夹角;β0——象鼻架前臂与后臂之夹角;α——象鼻架前臂与水平线之夹角;ω1——驱动臂架之角速度;Q——起重量。
X1——臂架(主动件);X2——象鼻架后臂;X3——后摇杆;X4——象鼻架前臂;X5——后摇杆下铰点O3与臂架下铰点O1之水平距离;X6——后摇杆下铰点O3与臂架下铰点O1之铅垂距离;X7——象鼻架的下沉量;X8——回转中心线与臂架下铰点O1之水平距离;R——幅度;γ——臂架与象鼻架后臂之夹角;θ1——臂架与水平线之夹角(自变量);θ3——后摇杆与水平线之夹角;β——A点速度向量与水平线之夹角;β0——象鼻架前臂与后臂之夹角;α——象鼻架前臂与水平线之夹角;ω1——驱动臂架之角速度;Q——起重量。
Figure 2. Schematic diagram of luffing mechanism of lemniscate type crane with boom driving
图2. 双纽线型起重机变幅机构示意图(臂架驱动)
双纽线型变幅机构的象鼻架为长型;在该变幅机构从最大幅度变化到最小幅度过程中,双纽线型的象鼻架呈上翘状或平置形。因此,当起升高度相同时,双纽线型的臂架系统轮廓的高度要低于普通型,且臂架系统的长度也低于普通型组合臂架,这对降低重心、改善起重机稳定性是有利的,提高了起重机的抗风能力。
从图2可知,这种变幅机构的臂架和后摇杆的活动范围很大、且臂架为主动件,另设有自重平衡系统。因此,其速度瞬心P的变化范围也大。为方便讨论,分二种情况:1)
,
,速度瞬心P在水平线的上方;2)
,
,速度瞬心P在水平线的下方。
速度瞬心P与臂架下铰点O1的距离计算。由正弦定理不难求得:
1)
时
(1)
式中:
.
2)
时
(2)
式中:
.
很显然,当
时,速度瞬心P在无穷远处。
2.2.
函数关系的求解
参考图2,由于臂架为主动件,所以
为输入条件,则后摇杆的摆动角
与自变量
构成函数关系;
的关系式可以依据封闭矢量方法如下求解。
由图2得,机架
、后摇杆
和臂架
、象鼻架后臂
构成封闭四边形。根据封闭矢量方程:
(3)
可以得到方程组:
(4)
式中:
Y、L——中间量。
进一步可求得
,见式(5)。
(5)
2.3. 象鼻架前端仰角α的求解
据图2可得象鼻架前端的仰角
,见式(6)。
(6)
式中:
.
2.4. 象鼻架轴心线与水平线夹角α1的求解
该型变幅机构在整个变幅作业过程中,象鼻架始终为上翘的形式,可以用象鼻架的轴心线与水平线的夹角
来表征。经过推演可得,见式(7)。
(7)
式中:
Y——见式(4)。
3. 水平分速度的求解
3.1. 吊点A的运动轨迹方程
该双纽线型变幅机构的象鼻架为长型,因此,它的变幅运动轨迹非常值得关注。象鼻架上的端点A的轨迹即为该变幅机构的轨迹,可由公式(8)得到。
(8)
式中:
α——见式(6)。
3.2. 吊点A的水平分速度求解
因该双纽线型变幅机构用于转载、过驳等装卸运输作业,变幅工作频繁,生产效率高,故对变幅工作速度有较高的要求。
在带载变幅工作过程中,人们更关心的是变幅速度的水平分量,也即吊点A的水平分速度VAX。
因变幅机构的铰接点B为臂架与象鼻架的共有点,故只能有一个速度VB。由VB可导出
,从而得到VA,最后可求得VAX;见公式(9)和(10)。
(9)
(10)
4. 变幅力矩的求解
变幅力矩是衡量变幅机构的重要性能指标之一,直接关系到变幅驱动功率的选取 [10] - [15]。
起重荷载经过象鼻架、臂架和后摇杆最终传递到整个起重机的基础上。变幅力矩是起重机结构设计的重要依据之一。变幅力矩MQ (对臂架的下铰接点O1)可由公式(11)求得。变幅力矩MQ的符号规定:使幅角
变小为正,反之为负。
(11)
5. 分析计算实例
由于没有双纽线型起重机(驱动臂架)的相关数据,但后摇杆驱动双纽线型起重机的数据可从文献 [16] 得到。因两者外形的相似性,故借用后摇杆驱动双纽线型变幅机构的已有数据,但此时自变量为角
。
文献 [16] 的数据信息有:X1 = 19.3 m,X2 = 6.5 m,X3 = 14.7 m,X4 = 16 m,AC = 22.3 m,X5 = 6.4 m,X6 = 5.3 m,最大外伸距(从回转中心线算) 30 m时
,最小外伸距10.5 m时
。起重量是16 t (160 kN)。
从文献 [16] 的数据信息可以推导出角
的活动范围是
,才能满足最大外伸距30 m和最小外伸距10.5 m的要求。根据前述的理论分析,结合MATLAB软件包编程分析计算可求得该双纽线型变幅机构的变幅特性结论:表1为分析计算结论、图3为速度瞬心P轨迹、图4为
函数关系曲线、图5为象鼻架轴心线与水平线夹角
变化曲线、图6为变幅运动轨迹、图7为水平分速度VAX、图8为变幅力矩MQ变化曲线图。

Table 1. Results of analysis and calculation
表1. 分析计算结论
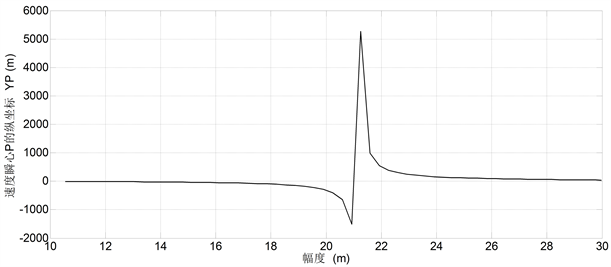
Figure 3. Locus of velocity instantaneous center P
图3. 速度瞬心P的轨迹

Figure 4. Relationship curve of
图4.
函数关系曲线
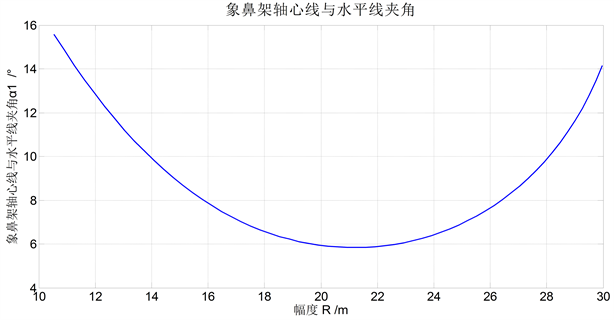
Figure 5. Curve of α1 between flying jib axis and horizontal line
图5. 象鼻架轴心线与水平线夹角α1变化曲线
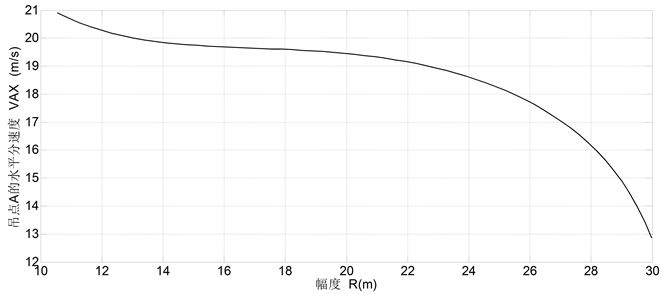
Figure 7. Curve of horizontal velocity of point A (supposed ω1 = 1)
图7. 吊点A的水平分速度(假设ω1 = 1)
6. 结论
对双纽线型起重机(驱动臂架)变幅机构的解析分析,实例分析计算表明:
1) 该型变幅机构的变幅运动轨迹近似为水平线,落差仅仅0.4098 m;其相对水平度为
;
2) 与后摇杆驱动双纽线型起重机 [7] 比较,其变幅过程的水平分速度约增大30%,对装卸转载作业有利;
3) 与后摇杆驱动双纽线型起重机 [7] 比较,其变幅力矩约增大10%~30%;
4) 该变幅机构可以推广应用于机器人的工作机构。