1. 引言
近年来,随着计算能力的提高与人工智能的飞速发展,神经网络被广泛应用于各个领域,包括用于数值求解各类微分方程 [1] [2] [3]。与有限差分法、有限元法等经典的数值方法不同,神经网络在高维偏微分方程数值求解问题上逐渐被使用。但目前没有任何一个理论,可以做一个先验判断,选择怎样的网络结构能达到良好的求解效果,这将会成为该领域重要的研究内容之一。解此类问题的神经网络又可以粗略地分为深度学习 [4] [5] [6] 和单隐层网络 [7] [8]。
Huangguangbin教授团队提出了极限学习机算法(ELM) [9],此算法表现出求解各种微分方程优异能力 [10] [11],它是基于一种离线的单隐层前馈神经网络,输出权重通过Moore-Penrose广义逆运算获得。该算法不仅训练速度快,避免了深度学习的梯度消失以及爆炸问题从而得到广泛应用。但对方程的解光滑性要求较高,需要解是连续的。
而深度学习大多根据梯度信息来更新权重,优化损失函数以此来求解方程,以美国布朗大学Karniadakis教授团队开发出物理信息神经网络为代表。此方法凭借着优秀的性能被广泛地应用于各类微分方程问题,他们通过将蕴藏在小样本数据中包含由物理定律等信息编码到深度网络中,提出了一种新的深度学习算法——内嵌物理机理神经网络 [12] [13] (Physics-informed neural networks, PINNs)。所以PINNs通常受到数据中包含的物理定律的约束,可以通过这些物理规律建模成时间相关的非线性偏微分方程。这样就可以利用PINNs发展出一类新的偏微分方程数值求解方法。该网络也可以有效地求解各类微分方程 [14] [15]。
近年来,一些研究人员将两种神经网络算法进行比对 [16],得出一些结论帮助人们根据解的类型选择合适的网络结构。本文针对同一类方程,对比网络的深浅,证明了网络深浅的适用性,ELM使用Moore-Penrose广义逆替代了梯度信息更新权重以达到损失函数最小化,PINNs则直接使用梯度信息优化权重使损失函数最小。虽然深度学习是神经网络发展的主流算法,但随着网络越深,所面临的问题变得越复杂,如:难以优化,训练时间长,内存空间大等。故本文对有连续解且求解区间范围较小的微分方程进行了理论证明以及实验,ELM优于一类使用梯度更新权重的深度学习算法。
2. 相关工作
2.1. 物理信息神经网络
考虑积分–微分方程的解的问题((1)~(2)):
(1)
(2)
若积分项的参数为0,那么((1)~(2))转换为微分方程,其中(2)为Dirichlet、Neumann、Robin或周期边界条件,对于时间相关问题,将时间视为的一个特殊分量,故包含时域。边值条件(2)可以简单地视为时空域上Dirichlet边界条件的一种特殊类型 [13];若微分项的参数为0,那么((1)~(2))转换为积分方程。
在PINNs中,首先构造一个神经网络,让输出
作为解
的近似,让
是L层神经网络,神经网络解输入为x,并且输出一个与
维数相同的向量。其中,
是神经网络中所有权重矩阵和偏置向量的集合。可以通过链式法则使用AD [17] 来求取微分,获得
关于其输入x的导数。
其次,需要约束神经网络的输出
以满足积分–微分方程和边界条件施加的物理条件。在训练中,我们取一些分散点(例如,域中随机分布的点或聚集点),分成两组训练点,内点
,边界点
,为了衡量神经网络输出,即微分方程的解
和约束之间的差异,定义损失函数为方程和边界条件残差L2范数加权和(采用均方误差(mean square error, MSE)) [13]:
(3)
其中
(4)
(5)
通过最小化损失函数训练神经网络,找出最优参数,即
(6)
利用训练好的神经网络模型,可以求解方程在任意时间和位置解。
2.2. 改进的极限学习机
对于此积分–微分方程((7)~(8))
(7)
(8)
搭建三角神经网络(TNN) [17] 对方程求解,对于M个输入,每个分量是
,有2N个隐层神经元。基于ELM设计的神经网络输出如下(采用正弦三角函数作为激活函数,即公式(9)~(11)):
(9)
构造试解:
(10)
初值:
(11)
将(9) (10)带入(7),得到合并同类项得,改写成矩阵形式为:
(12)
通常无法获得定积分
的原函数表达式,因此我们使用复化辛普森求积公式来获得数值积分,如下所示:
(13)
本文方程中只有一个初值条件。添加条件(11)最终得到(14):
(14)
其中
,W为隐藏层的权重矩阵,Y为输出,即是每个输入点的数值解。
ELM采用最小二乘法直接计算W,使其误差最小化,代替传统梯度下降算法的重复迭代,计算公式如下:
(15)
其中,
是矩阵H的Moore-Penrose广义逆,
。
注意到q是一个需要确定的参数,有必要确定函数中的三角激活函数参数q,该q值的选择直接影响解的精度,在Zhou [18] 的论文中没有给定q的选取方法,本文使用经常被用于选取最优参数的粒子群优化算法 [19],本文称之为粒子–三角神经网络(PSO-TNN)。我们使用粒子群优化算法最小化MSE(也可以选择相同类型的评估误差指标)来选取q,从而实现三角激活函数的优化。
2.3. 理论证明
定理1:对于物理信息神经网络
i) 若选用sigmoid/tanh激活函数,对于此积分微分方程((7)~(8)),权重更新梯度为0向量。
ii) 若选用relu激活函数,对于此积分微分方程((7)~(8)),定义域是恒大于0的,由
,仅对输入点做线性加权,方程的解一般为非线性,若用线性拟合非线性误差会很大。
i) 证明:
进行预定义,由于
,机器精度只达到10−16,故定义若有
,那么认为
。
对于积分微分方程(7~8),积分项
采用 的Gaussian-Legendre求积式公式如下:
的Gaussian-Legendre求积式公式如下:
(16)
其中
是Legendre多项式的零点,
,采用物理信息神经网络求解该方程,取点N个,
,初始化方式将权重矩阵W置为1,偏置向量
置为0向量。
网络结构为一层隐藏层(为了证明方便,与多层隐藏层网络结构结构相似),神经网络解为
。
首先,将区间分为
和
,其中
,且
。故
,都有
。
根据 [13] 将损失函数写出来有
(17)
其中,
(18)
根据损失函数(17)~(18),写出梯度如下
(19)
其中i和k代表第k层的第i个神经元,
代表第
次更新的梯度,现有s个点
,
,且
,有
,代回(19)得到
,使用ADAM优化算法 [20],参数更新如下:
(20)
其中
,
;
,
,
;通常
,
,
,
为步长,可取10−1~10−3。再将
带入(20),得到
,即梯度消失。难以优化,权重更新停止,导致了物理信息神经网络解的误差很大。
定理2:若微分方程的解
是间断的,以间断点为界写成分段函数,误差由分段函数的子函数距离空间衡量。
证明:采用三角激活函数,构造微分方程试解
。其中微分方程
解空间的基为
,因三角函数具有正交性,它的基可由三角函数构成。可将不连续函数写为分段函数。那么由分段点,写为两个及两个以上函数,以两个为例进行证明:
将解
改写为
。
1) 若
和
都为有界函数。那么分别用三角函数作为基函数
和
,其中
,
,
。那么误差
2) 若
和
至少有一个不存在或者无界函数,那么至少有一个不能使用三角函数作基函数表示。
综上,若这几个函数空间皆为有界函数,那么误差是有限数。若有一方为
或不存在,那么误差是无限或不存在。
推论1:若解函数的间断点为第一类不连续点和第三类间断点的在间断点有定义的情况,那么误差为有限的,可以使用ELM求解方程;若为第二类间断点和第三类间断点的在间断点处无定义的情况,那么误差是无限或不存在,不可使用ELM求解方程。
推论2:对于区间是
的微分方程。
i) 当使用sigmoid/tanh激活函数,
或
时,且解是连续的不适于使用梯度信息优化的深度学习的使用求解微分方程。
ii) 当使用relu激活函数,当
或
或
时,且解是连续的不适于使用梯度信息优化的深度学习的求解微分方程。
iii) 当解是连续的,ELM适用于求解此类微分方程。
3. 实验测评
1) 这里以数值实验来验证的定理1 i)。
2) 使用PSO-TNN和TNN以及PINNs,求解索赔额服从Pareto分布的经典风险模型的破产概率问题,此问题被证明为以下积分–微分方程 [21] [22]:
其中
,该问题没有解析解,但是已知一些点的解,如表1。

Table 1. Exact solutions of known points
表1. 已知准确解的点
采用神经元个数
的PSO-TNN和TNN以及神经元个数
和层数
的PINNs求解这该方程,样本集为,
,
,
数值实验结果如下:
表2和图1描述了此方程的精确解、PSO-TNN和TNN以及PINNs的数值解及其相应的误差。由表2中数据可知,对于已知点,PSO-TNN的MSE为8.91703e−08,由 [17] 中的TNN获得的MSE约为7.1372e−07,而由PINNs获得的MSE约为2.2680e−01。对于未知点,PSO-TNN和TNN的数值解非常相似。因此,PSO-TNN的解非常接近精确解。从训练时间上,PINNs时间为1293.0747 s,而PSO-TNN仅需要2.3057240 s。故对于定义域区间范围较大的方程,从训练时间还是误差,ELM都优于深度学习。
若对于此方程的区间进行截断,只取样本集为,
,数值解如表三。由表2可知,当方程自变量的区间右端点的值较小时,PINNs可以把方程的解学习得较好,MSE约为2.3297e−07,可以较好地近似该方程的解。

Table 2. Error and time of three algorithms in different intervals under Pareto distribution
表2. Pareto分布下不同区间三种算法的误差以及时间
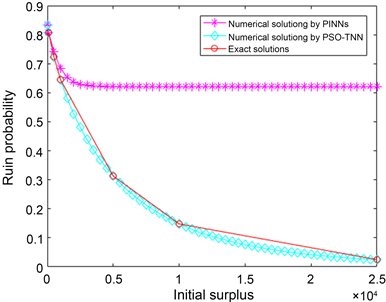
Figure 1. Numerical and analytical solutions by PINNs, PSO-TNN in (1)
图1. (1)的PINNs, PSO-TNN数值解以及准确解
2) 使用PSO-TNN和TNN以及PINNs,求解索赔额服从指数分布下的经典风险模型的破产概率问题,此问题被证明为以下积分–微分方程 [21] [22]:
其中
时,该问题的解析解为
,先采用神经元个数
的PSO-TNN和TNN以及神经元个数
和层数
的PINNs求解该方程,其后增加神经个数再进行比对,样本为:
数值实验结果如下:
表3和图2描述了此方程的精确解、PSO-TNN和TNN以及PINNs的数值解及其相应误差。由表3中数据可知,PSO-TNN的MSE为1.6967e−10,由 [17] 中的TNN获得的MSE约为4.1665e−06,而由PINNs获得的均方误差约为6.8827e−08。虽然PINN同样优于原始TNN,但训练时间远长于PSO-TNN和TNN。虽然PINN同样优于原始TNN,但训练时间远长于PSO-TNN和TNN。显然,PSO-TNN优于TNN和PINNs。PSO-TNN的解可以非常接近精确解。从训练时间上,PINNs时间1124.6291 s,而PSO-TNN仅需要0.0406790s。故对于定义域区间范围较大的方程,从训练时间还是误差,ELM都优于深度学习。与(1)进行比较,发现同类型的积分–微分方程,当区间不同,对于求解方法的网络结构是大相径庭的。

Table 3. Error and time of three algorithms under exponential distribution
表3. 指数分布下的三种算法误差和时间
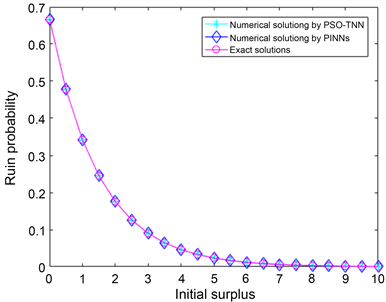
Figure 2. Numerical and analytical solutions by PINNs, PSO-TNN in (2)
图2. (2)的PINNs, PSO-TNN数值解以及准确解
4. 结束语
本文以经典风险模型下的积分–微分方程为背景,分别使用了改进的极限学习机和使用梯度信息优化的深度学习的最具代表性算法之一PINNs进行求解比较研讨,通过理论证明了积分–微分方程((7)~(8)),当区间为
时,选用sigmoid/tanh激活函数,使梯度为0,不适合使用PINNs求解方程;选用relu激活函数,用线性的试解去拟合非线性的真实解,导致误差很大。再将结论推广到了一类使用梯度更新的深度学习算法和微分方程上,又证明了解为不连续函数会由间断点的类型决定是否适用ELM。又通过实验验证了上面的理论,实验表明当
且
时,使用PSO-ELM和PINNs的误差相近,但是若有时间需求可选用PSO-ELM。本文对于两种方法进行对比探究,可以根据方程类型直接选定求解算法,避免了逐个验证,节省了计算资源和时间。 [23] 中表现出了PINNs的对拥有间断点的微分方程良好的近似能力,未来的发展可以改进PINNs使它适用于推论2中且解是非连续的方程。
基金项目
贵州省科技计划项目(黔科合平台人才[2020]5016),贵州大学一流课程培育项目(XJG2021040);贵州大学教改项目(XJG2021027);贵州大学研究生创新人才计划项目。