1. 引言
土壤水分(soil moisture, SM)是水文的主要状态参量,在陆地水、能量和碳循环之间的联系中起着重要作用,控制着水文气象、水文气候和生物地球化学过程 [1]。在农业应用中,土壤水分不仅是作物生长发育的基本条件,同时也是作物产量估算和干旱监测的关键参数,因此准确获取土壤湿度具有重要意义 [2] [3]。传统的单点测量土壤湿度虽然精度高,但受地表覆盖(如植被、地形和土壤质地)强空间异质性的影响,土壤湿度仅在小空间尺度上具有代表性 [4]。相对于烘干法、电阻法等传统的土壤湿度监测方法,光学遥感技术具有高效率、低成本、大范围、高分辨率、快速获取和动态监测能力强等优点 [5],基于光学遥感的土壤湿度反演受到了众多学者的关注,同时也是目前遥感技术应用的重要发展方向 [6] [7]。
利用可见光和近红外波段在不同地表覆盖下反射率间的差异性,归一化植被指数(normalized difference vegetation index, NDVI)、基于两波段增强型植被指数(two-band enhanced vegetation index, EVI2) [8]、垂直干旱指数(perpendicular drought index, PDI) [9]、修正垂直干旱指数(modified perpendicular drought index, MPDI) [10]、植被调整垂直干旱指数(vegetation adjusted perpendicular drought index, VAPDI) [11] 等土壤湿度指数模型先后被提出。基于这些指数模型,学者们进行了大量的土壤湿度反演研究。张月等 [12] 采用NDVI和EVI指数模型监测藏北牧区土壤湿度,发现二者与土壤湿度间均呈现较强的相关性;李喆等 [13] 以湖北漳河灌区为研究区域,验证了PDI模型在湿润地区监测土壤湿度的可行性;杨学斌 [14] 等在内蒙古干旱监测中发现,由于顾及了植被覆盖的影响,MPDI相较于PDI模型具有更高的SM监测精度;吴春雷等 [11] 针对PDI在农田植被覆盖区监测精度降低的问题,提出了一种适于植被覆盖下的SM植被调整垂直干旱指数,并验证了VAPDI模型在农田植被区监测土壤水分的适用性。总的来说,以上指数模型针对具体的研究场景都取得了较高的精度。但指数模型均是基于不同波段在不同地表环境下的反射辐射特性而构建的,除要求具备较强的遥感背景知识,且大多需要确定土壤线,实际操作较为困难。此外,在中高度植被覆盖下,NDVI容易发生饱和,导致其不能很好地反映植被的生长状况,从而可能降低SM的反演精度。机器学习方法能够发现隐藏于数据间有意义的内在关联,一定程度上可以克服上述问题,如卷积神经网络 [15]、支持向量机 [16]、随机森林 [17] 等已经成功地应用于土壤水分反演,但这些机器学习方法大都需要海量的样本数据,对小样本容量数据的建模却难以胜任。
作为我国第一颗地球同步轨道遥感卫星,高分四号卫星(GF4)具备高时间分辨率和较高空间分辨率的优势,已成功运用于森林火灾监测 [18]、洪水灾害监测 [19]、水体提取 [20] 和气溶胶监测 [21] 等,但其在土壤湿度反演方面的研究却鲜有报道。线性回归作为一种简单的机器学习算法,具有原理简单、易于实现和对建模数据量要求较少等优点。因此,为充分挖掘GF4的环境监测能力和克服指数模型构建和土壤线确定困难的缺点,本文以GF4红光和近红外波段的地表反射率,以及由红光和近红外波段地表反射率计算得到的宽范围动态植被指数(WRDVI)为解释变量,以土壤湿度实测值为目标值(因变量),构建基于GF4的土壤湿度多元线性回归预测模型(下称MLR_W模型),并对MLR_W、SM_P、SM_M、SM_V和MLR_N的模型拟合精度和SM反演精度进行了实验对比分析。
2. 研究区概况与数据源
2.1. 研究区概况
贵阳市地处云贵高原黔中山原丘陵中部(研究区位置见图1),长江与珠江分水岭地带,介于东经106˚07'~107˚17'、北纬26˚11'~26˚55'之间,辖区范围包括息烽县、修文县和开阳县3个县、清镇市和云岩、南明、花溪、乌当、白云、观山湖6个区。贵阳地势西南高、东北低,海拔高度在1100米左右,常年受西风带控制,属于亚热带湿润温和型气候,年平均气温为15.3℃,年极端最高温度为35.1℃,年极端最低温度为−7.3℃,年平均相对湿度为77%,年平均总降水量为1129.5毫米。此外,贵阳受云覆盖影响严重,常年无云“清洁日”较少,很难获得一幅完整的无云层影响的光学遥感影像。
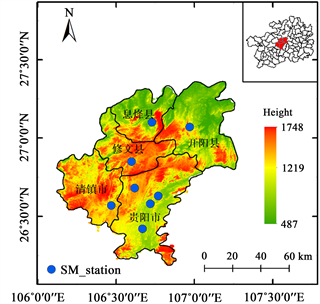
Figure 1. Location of study area and distribution of soil moisture monitoring stations
图1. 研究区位置和土壤水分监测站分布
2.2. 数据源
2.2.1. 土壤水分
如图1所示,贵阳市辖区内共有8个农气土壤水分自动监测站,其中贵阳市区3个,清镇市1个,息烽县、开阳县和修文县各1个。根据遥感影像受云层影响的情况,筛选出2016年5月~2021年11月共80个SM观测值。实验采用的土壤水分数据为0~10 cm土壤表层含水率,其中60个用于模型的构建,未参与建模的20个用于模型性能的评价。
2.2.2. 遥感数据
研究采用GF4全色多光谱(PMI)传感器(相关技术指标如表1所示) 50 m空间分辨率的遥感影像作为数据源,产品为1A级(相对辐射校正产品)TIFF格式影像,主要波段为红光波段、近红外波段,相关数据可从中国资源卫星应用中心下载(https://data.cresda.cn/)。为了减少大气和云层对实验结果的干扰,筛选出图像云层量小于10%的高分数据,成像时间为:2016年5月~2021年11月,共10景。

Table 1. Technical specifications of GF-4
表1. GF-4有效载荷技术指标
GF4遥感卫星影像的预处理包括绝对辐射定标、大气校正、正射校正、图像配准和图像裁剪等,最终得到光谱反射率。首先,通过中国资源卫星应用中心获取的最新定标参数,进行辐射定标;其次,利用ENVI的FLAASH Atmospheric Correction工具完成大气校正;然后利用30米DEM数据(来源)和Landsat 8 30米多光谱数据进行正射校正以及图像配准,30米DEM数据和Landsat 8 30米多光谱数据均源于地理空间数据云(http://www.gscloud.cn/)。
3. 研究方法及精度评价指标
3.1. 垂直干旱指数
在二维空间中,土壤在红光(red)波段和近红外(near infrared, nir)波段的光谱反射率呈线性关系,由此拟合出来的直线称之为土壤线,可表示为:
(1)
式(1)中:M为土壤线斜率;I为土壤线在纵坐标上的截距;Rnir和Rred分别为近红外波段和红光波段光谱反射率。
受土壤水分对遥感辐射强吸收的影响,裸土反射率随着土壤水分的增加而显著下降,这种现象在近红外波段表现得更为明显。基于红光波段和近红外波段反射率随土壤水分的变化特征,Ghulam等 [9] 提出了一种垂直干旱指数(PDI)模型。
(2)
3.2. 修正垂直干旱指数
植被冠层组织强烈吸收蓝、紫、红三种波长的入射辐射,并强烈反射近红外光谱;植被密度越厚,红色波段反射率越小,而近红外波段反射率越高,显然PDI指数未考虑植被的影响。为此,Ghulam等 [10] 顾及植被覆盖的影响,建立了修正垂直干旱指数MPDI。
(3)
式(3)中:
和
分别为植被在红光和近红外波段的反射率,取研究区中植被覆盖度处的红光反射率和近红外反射率;
为植被覆盖度,其计算公式为 [10]:
(4)
式(4)中:NDVIv和NDVIs分别表示研究区中裸土和植被的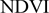 。NDVIv和NDVIs分别取研究区中
。NDVIv和NDVIs分别取研究区中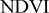 的最大值和最小值。NDVI为植被指数,其计算公式为:
的最大值和最小值。NDVI为植被指数,其计算公式为:
(5)
3.3. 植被调整垂直干旱指数
为进一步减小混合像元中植被因素的影响,提高土壤水分的反演精度。吴春雷等 [11] 在PDI的基础上引入表征植被覆盖度的垂直植被指数(perpendicular vegetation index, PVI),继而提出了适用于植被覆盖下的植被调整垂直干旱指数VAPDI。
(6)
式(6)中:PDI(A)、PVI(A)分别表示PVI最大值点A对应的PDI、PVI指数,其中PVI的计算公式为:
(7)
由上述计算公式可看出,SM_P、SM_M和SM_V模型的构建本身较为复杂,且都需要预先确定出土壤线的斜率M和截距I,而M和I的解求无疑是一个繁琐的过程,这势必将增加指数模型反演土壤水分的复杂度。
3.4. 宽范围动态植被指数
在中高度植被覆盖条件下,近红外波段反射率不断上升,而红光波段反射率不断下降,导致NDVI逐渐接近饱和。Gitelson [22] 等通过引入加权系数a (
)来减小Rnir和Rred对NDVI贡献的差异,提出了一种宽动态植被指数(WDRVI)。通过增强动态范围,使用与NDVI相同的波段,WDRVI能够对作物生理和物候特征进行更为可靠的表征。
(8)
根据研究区植被覆盖情况,本文a取值为0.15 [22]。
3.5. 多元线性回归
由上述分析知,土壤含水量和植被覆盖度都会影响红光波段和近红外波段的反射率,因此为简化土壤水分反演模型的构建过程,本文直接以红光波段反射率、近红外波段反射率和植被指数(NDVI、WRDVI)为协变量,以实测SM为因变量,采用多元线性回归方法构建土壤水分反演模型,具体算式如下。
(9)
式(8)中:a、b、c、d均为待定系数,可采用最小二乘得以解求;SM为土壤水分测量值,VI为植被指数。多元线性回归原理和方法参见文献 [23],此处不再赘述。
3.6. 精度评价指标
为了全面客观地评价模型性能和精度,采用均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2) 3个指标来评价模型精度。其中,MAE能很好的表达观测值误差的情况,R2表征因变量的全部变异能被自变量解释的比例,RMSE表示观测值偏离真实值的离散程度,各指标计算公式如下:
(10)
(11)
(12)
式中,n为样本总数,
和
分别为变量y的预测值(或拟合值)和平均值,本文中y为土壤水分SM。
4. 土壤水分反演模型的建立
4.1. 土壤线参数确定
获取土壤线的方法通常有两种:常规方法和自动算法 [24]。其中常规方法是在ENVI5.3中按照分类图像选出纯净裸土像元,并在Nir-Red二维光谱空间中拟合出土壤线;自动算法通过自适应区间选择来自动获取土壤线参数。本文拟采用自动算法获取土壤线,具体操作步骤如下:① 利用土壤覆被分类对预处理后的GF4影像中的水体部分进行掩膜剔除。② 在ENVI5.3的Scatter Plot工具中,将影像的Band4作为横坐标、Band5作为纵坐标绘制二维平面散点图,使用ROI(region of interest)工具将图中分布于较下方的散点提取出来。由于遥感影像的像元数量过多,大大降低了寻找所有土壤点(横坐标所对应最小纵坐标值的点)的效率,因此将散点中Band4反射率的最大值与最小值的差值分为100组,将平均值作为组长,找到每组Band4中对应的最小Band5反射率值,组成初始土壤点集。分别计算以横坐标总区间范围的0%~50%,0~75%,0%~100%,25%~75%,25%~100%,50%~100%为区间子集得土壤点集的相关系数,对原始的土壤点集进行进一步筛选,取相关系数最大的为最佳横坐标区间,得到最终的土壤点集;最后,采用最小二乘法拟合方程即可得到土壤线参数(图2)。
由图2可以看出,土壤线斜率为0.9392、线截距为0.0648;决定系数R2为0.9602,说明红光波段和近红外波段反射率在二维空间中的相关性极强。
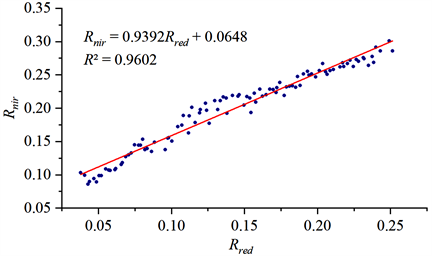
Figure 2. Automatic algorithm extraction of soil line fitting results
图2. 自动算法提取土壤线
4.2. 土壤水分反演模型的建立
4.2.1. 基于土壤干旱指数的SM模型
基于预处理后的遥感影像数据,提取研究区8个土壤水分监测站对应位置处的反射率Rred和Rnir,并将Rred、Rnir、土壤线斜率M和截距I分别代入(2)式、(3)式和(7)式,求取不同时间各站点处的PDI、MPDI和VAPDI值。以60个SM监测值为因变量,以与SM监测同址且时间同步的PDI、MPDI和VAPDI为解释变量,基于一元线性回归模型建立基于干旱指数的SM预测模型。各指数模型拟合情况如图3和表2所示。

Figure 3. Fitting effect of drought index model
图3. 干旱指数模型拟合效果

Table 2. Model equation and modeling accuracy statistics
表2. 模型方程及建模精度统计
4.2.2. 基于多元线性回归的MLR_N和MLR_W模型
为克服干旱指数构建困难和确定土壤线过程较为复杂的缺陷,多元线性回归法直接采用与SM同址且时间同步的Rred、Rnir和植被指数(NDVI、WRDVI)为自变量,以相同的60个SM监测值为因变量,基于最小二乘法分别建立SM反演模型(MLR_N和MLR_W),模型房产和各模型拟合情况如表2所示。
结合图3和表2可以看出,基于GF-4遥感影像得到的PDI、MPDI、VAPDI 3种指数与土壤水分实测值均呈显著负相关,SM_P、SM_M、SM_V、MLR_N和MLR_W土壤水分拟合值与实测值间的决定系数R2分别为0.574、0.644、0.682、0.675和0.681,说明PDI与SM为中等程度相关,而其余模型解释变量和SM间均表现为强相关;建模MAE分别为5.79%、5.30%、5.15%、5.09%、5.05%,RMSE分别为7.38%、6.75%、6.38%、6.45%、6.38%。进一步分析知,SM_M、SM_V、MLR_N和MLR_W的拟合效果和建模精度均要明显优于SM_P,这是因为在Nir-Red二维光谱特征空间中,各像元的反射率由土壤和植被等背景地物共同决定,SM_P模型未顾及植被覆盖对土壤光谱信息的影响,因此无法完全反映出表层土壤水分的实际水平。同时,基于多元线性回归的MLR_W模型优于MLR_N模型的建模精度,且避免了构建指数模型和解土壤线方程的复杂过程,在土壤水分反演方面更具便捷性。此外,在显著性水平0.01下,F检验所得P值均小于0.01,说明各回归方程整体性显著,即各方程解释变量对因变量都具有较强的解释性。
5. 试验结果与分析
以未参与建模的Rred、Rnir、NDVI、PDI、MPDI和VAPDI分别作为各模型的输入变量,以同址且时间同步的SM监测值为参考值,采用平均绝对误差和均方根误差作为精度评价指标,对各模型的预测能力进行评价,得表3所示的精度统计结果。
由表3可知,预报精度由高到低的顺序依次为SM_M > MLR_W > MLR_N > SM_V > SM_P,原因可能是在光谱反射率中,红光和近红外波段的细微变化对最终结果会产生比较大的影响,其中植被对红光波段有较强的吸收性、对近红外波段有较强的反射性,但是SM_P模型却忽略了这一影响。换言之,SM_P模型主要适合于裸土或者植被稀疏的地区。经fv修正的SM_M模型、经PVI修正的SM_V模型和引入NDVI和WRDVI的MLR_N和MLR_W模型,均考虑了植被覆盖的影响,因而取得了较高的预测精度。基于土壤干旱指数的SM_M模型较MLR_W模型的预测精度更高,二者间MAE和RMSE差值分别为0.51%和0.33%,但MLR_W模型无需确定土壤线参数,因此更易于实施。此外,MLR_W模型较MLR_N模型进一步改善了预测精度,说明采用WDRVI可一定程度上克服NDVI在中高度植被覆盖下易出现饱和的缺陷。
6. 结论
采用2016~2021年高时空分辨率的GF4遥感影像作为数据源,以贵阳市为研究区域,基于高分四Rred、Rnir和WRDVI,采用多元线性回归构建了贵阳市SM预测模型,实验结果表明:
1) 基于GF-4遥感影像数据,SM_P、SM_M、SM_V、MLR_N和MLR_W均取得了较高的建模精度,决定系数R2分别为0.574、0.644、0.682、0.675和0.681,统计学上除SM_P模型解释变量和因变量表现为中等程度相关外,其余模型解释变量和因变量间均表现为强相关;模型拟合精度最高的为SM_P模型,其次为MLR_W和MLR_N。
2) 相较于SM_P指数模型,SM_M、SM_V、MLR_N和MLR_W模型具有更多的适宜场景,SM预测结果也更加精准,在有植被覆盖的情况下,四种模型均可获得较高的反演精度。当数据量较小且存在中高度植被覆盖时,针对指数模型构建困难和相关参量解求过程较为复杂的缺陷,直接基于多元线性回归构建的MLR_W土壤水分预测模型不失为一种更优的选择。
基金项目
国家自然科学基金项目(52064005);贵州省省级科技计划项目(黔科合支撑[2022]一般224)。
NOTES
*通讯作者。