1. 引言
生物系统是一个非常复杂的系统,它与人类的生存、人们的健康和社会的发展密切相关。研究生物系统的动态特性具有重要意义。捕食是物种之间的重要相互作用的活动表现,其动力性行为被广泛研究 [1] [2] [3]。在现实世界中,人口增长可以分为几个生理功能差异显著的阶段,例如幼年、成年和老年,幼年通常不具有生育能力、捕食能力和传播能力。因此,许多学者考虑具有阶段结构的种群模型 [4] [5] [6]。参考文献 [4],我们提出并研究了以下阶段结构的具有时滞的食饵–捕食者微分动力系统:
(1)
其中
和
分别代表时间t的幼年和成年食饵密度,
代表时间t的捕食者密度。假设幼年食饵的繁殖率与现有的成年食饵种群的繁殖率成正比,其比例常数为
,
是幼年食饵种群的死亡率。时滞
表示食饵种群从出生到成年的时间,
表示幼年食饵种群向成年食饵种群的转变。成年食饵种群的死亡率为
和增长率为m,捕食者种群的死亡率为
和增长率为w。
为捕食系数,
为捕食者捕食食饵的转化率,又称消化系数。
对于哺乳动物来说,幼年食饵隐藏在自己的巢穴中,由父母抚养,它们不需要外出觅食,因此不容易受到捕食者的攻击,也不会受随机因素的影响。因此,本文引入了以下带有时滞k的食饵–捕食者微分动力系统:
(2)
随机因素的影响在生物系统各要素之间非常常见,如人与人之间的交流,总是存在许多不确定因素。在一个生态系统中,各种随机因素的干扰无处不在,当随机因素的影响很小时,许多模型可能会忽略,但是忽略随机因素的作用可能导致相当大的偏差 [7] [8] [9],一个合理的解释是,当外界干扰越小时,生态系统偏离平衡状态越小,各个种群之间越容易达到平衡。因此,与确定性模型相比,随机模型将更好地描述生物系统本身并反映实际问题的本质。许多学者将布朗运动作为随机因素添加到确定性生物模型中,然后利用随机微分方程理论研究随机动力学行为。参考文献 [10] [11],对噪声的一个合理的数学解释是所谓的白噪声,它正式被认为是布朗运动
的导数,即
。参考文献 [12],假设系统受到随机白噪声扰动的影响,该随机白噪声扰动与系统状态
和平衡状态
的偏差成正比。当偏差越大,随机扰动也越大,当处于平衡状态时,随机扰动为零。这种随机扰动也被许多研究者所接受并应用 [13] [14]。于是,得到了具有时滞k的食饵–捕食者随机微分动力系统:
(3)
其中
表示随机白噪声扰动的强度。
是定义在完全概率空间
上的布朗运动。
和
是正常数,
,
表示幼年食饵向成年食饵的转变,时滞k (正整数)表示食饵从出生到成熟的时间。
大部分的随机系统都是研究连续时间情况下的模型,但是由差分方程组成的离散时间模型比连续时间模型更合适。因为实际情况下的数值模拟,离散时间模型比连续时间模型的效果更好。此外,关于差分方程描述的随机离散模型的稳定性的研究也很少。于是,本文通过Euler-Maruyama离散化方法 [15] 得到具有时滞k的食饵–捕食者随机离散系统,并研究该系统在平衡态的稳定性。
(4)
其中h是步长,初始条件
,
是一个相互独立的适应
的随机变量序列,且满足:
(5)
其中E是期望。
系统(4)有两个边界平衡点:
;
且
;
和一个正平衡点:
且
。
本文主要研究具有时滞k的食饵–捕食者随机离散系统(4)的正平衡点和边界平衡点的稳定性。首先给出了一些定义、定理和规范形式,在正平衡状态和边界平衡状态下线性化系统(4),分别得到了具有随机扰动的非线性差分方程在正平衡状态下的渐近均方稳定性的充分条件和边界平衡状态的几乎确定的渐近稳定性;并通过给定参数对模型进行了数值模拟验证结论的正确性。
2. 正平衡状态的渐近均方稳定性
由于本文的目的是考虑这些平衡点的稳定性,为此需将非线性的随机离散系统线性化。记正平衡点
,令
:
(6)
对平移变换后的(6)进行Jaccobi线性化,得到正平衡状态下的具有时滞k的食饵–捕食者随机离散线性系统:
(7)
对于边界平衡点
,令
:
(8)
对平移变换后的(8)进行Jaccobi线性化,得到边界平衡状态
下的具有时滞k的食饵–捕食者随机离散线性系统:
(9)
记边界平衡点
,令
:
(10)
对平移变换后的(10)进行Jaccobi线性化,得到边界平衡状态
下的具有时滞k的食饵–捕食者随机离散线性系统:
(11)
令
,平衡状态
,系数矩阵:
以及
得到规范形式:
定义2.1对于两个对称矩阵P和Q,如果
,则
是正定矩阵。
定义2.2对于任意Lyapounvo函数
,定义算子:
定义2.3如果
,
(
),使得
,则系统(7)的零解是均方稳定的;如果
,则是渐近均方稳定的。
引理2.1 ( [16] 的定理1.1) 对于线性化后的系统(4),假设存在满足
的非负泛函
和
,那么系统(7)的零解是渐近均方稳定的。其中
,
是正常数。
引理2.2 ( [16] 的引理1.3) Q为正定的
矩阵,对矩阵
,有
(12)
其中
代表转置。
定理2.1 假设对于某个正定的
矩阵P和Q,若矩阵方程
(13)
有半正定解D,则系统(7)的零解是渐近均方稳定的。
证明考虑一个由
定义的Lyapounvo函数,其中
,
均为正定对称矩阵。
首先计算
的期望值:
通过引理2.2,令
和
,由(12)有
根据(5),计算
的期望值:
因此有:
其中
,
。
现在,设
,定义
。则
接下来,计算
的期望值:
其中
,
是一个正常数。因此得到系统(4)的零解是渐近均方稳定的。
应用定理2.1去分析系统(7),系统(7)的系数矩阵:
求解矩阵方程(13)得到:
(14)
注2.1不难看出,系统(7)的零解的稳定性等同于线性化的系统(4)的正平衡解
的局部稳定性。如果在平衡点
处存在正定矩阵P和Q,以及一个半正定解D满足矩阵方程(13),则系统(7)的零解是渐近均方稳定的。
理论上,可以求解
,然后验证是否存在正定矩阵P和Q,以及一个半正定解D满足矩阵方程(13)。然而,因为涉及太多的参数,所以本文只提供一个具体的例子。
设
(单位矩阵),选择参数
,
及初始条件
。
代入系统(4),得到正平衡点
;系数矩阵:
求解矩阵方程得到
。
由注2.1,矩阵P是正定的,因此系统(7)的零解是渐近均方稳定的,系统(4)的正平衡点
是局部渐近均方稳定的。数值模拟见图1,图中显示加入随机扰动后,系统(4)的正平衡状态收敛于
。
3. 边界平衡状态的几乎渐近稳定性
当我们用定理2.1讨论其他2个边界平衡点时,没有一个具有均方稳定性。当这种情况发生时,Palmer [17] 通过离散化的Itô公式研究了线性随机差分方程的几乎确定的渐近稳定性。
定义3.1如果
,则线性化的系统(4)的零解是几乎渐近稳定的。
引理3.1 ( [17] 中的引理5.3)
是差分方程
的解,
,
且足够小,则有以下结论:
1) 当且仅当
,几乎确定的有
;
2) 当且仅当
,几乎确定的有
。
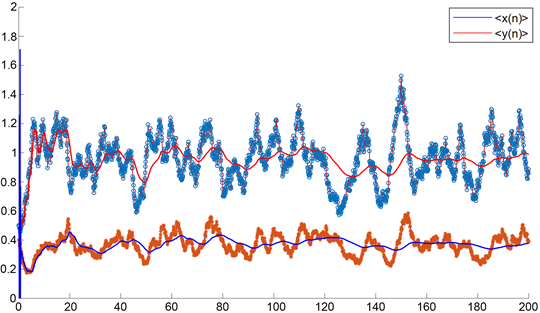
Figure 1. The positive equilibrium
is local asymptotically mean square stable
图1. 正平衡状态是
局部渐近均方稳定的
考虑边界平衡点
,对应系数矩阵:
无法找到半正定解D使矩阵方程(13)成立。线性化的系统(4)为系统(9):
(9)
对系统(9)的第二个差分方程,应用引理3.1。因为
均为正常数,
,则
是肯定的。
对于对系统(9)的第一个差分方程:
因为
,则有
。
注3.1若
,则系统(4)的边界平衡状态
是几乎渐近稳定的。
选择参数:
及初始条件
。
数值模拟结果见图2,系统(9)的零解是混乱且不规则的,对应的边界平衡状态
是不稳定的。
选择参数:
及初始条件
。
数值模拟见图3,系统(9)的零解收敛于
,对应的边界平衡状态
是几乎渐近稳定的。
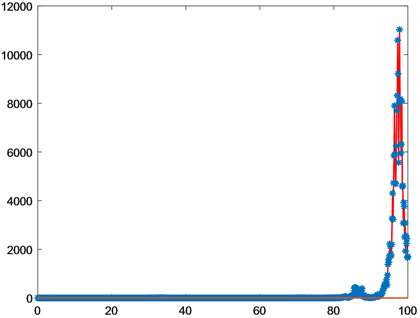
Figure 2. The boundary equilibrium state
is unstable
图2. 边界平衡状态
是不稳定的
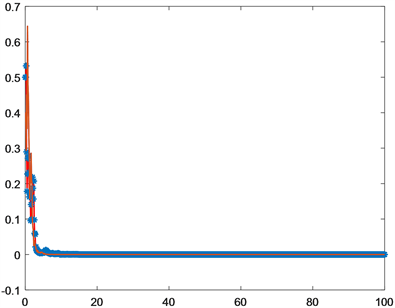
Figure 3. The boundary equilibrium state
is almost surely asymptotic stable
图3. 边界平衡状态
是几乎渐近稳定的
考虑边界平衡点
,对应系数矩阵:
无法找到半正定解D使矩阵方程(13)成立。线性化的系统(4)为系统(11):
(11)
对系统(11)应用引理3.1,若
,则
,且
是肯定的。
注3.2若
且
,则系统(4)的边界平衡点
是几乎渐近稳定的。
选择参数:
及初始条件
。
数值模拟结果见图4,系统(11)的零解是混乱且不规则的,对应的边界平衡状态
是不稳定的。
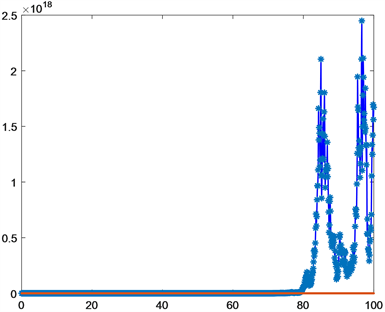
Figure 4. The boundary equilibrium state
is unstable
图4. 边界平衡状态
是不稳定的
选择参数:
,初始条件
。
进行数值模拟,结果见图5,系统(11)的零解收敛于
,对应的边界平衡状态
是几乎渐近稳定的。
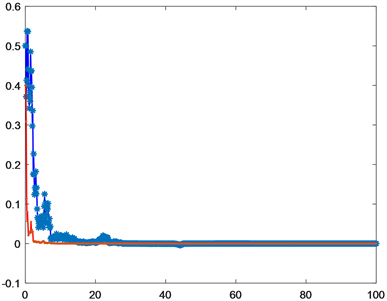
Figure 5. The boundary equilibrium state
is almost surely asymptotic stable
图5. 边界平衡状态
是几乎渐近稳定的
4. 总结
在本文中,提出并研究了随机的食饵–捕食者离散时滞模型,并假设随机白噪声扰动与系统状态和平衡状态的偏差成正比。对于正平衡状态,通过Lyapunov函数方法得到了渐近均方稳定性的充分条件。但是,应用这种方法来获得另外两个边界平衡状态的均方稳定性似乎并不容易。对于边界平衡状态,通过使用离散化的Itô公式和相关定理研究了它们的几乎确定的渐近稳定性。同时,本文提供了一种解决随机离散时滞模型在正平衡状态下判断渐近均方稳定性问题的通用结论。获得的理论结果得到了数值模拟的有力支持。只要系统参数和白噪声强度满足我们给出的条件,系统就会稳定在平衡状态。将来,我们可以将随机离散模型与神经网络模型结合,复杂神经网络加入随机扰动后,已成为重要的研究方向。通过大量数据的拟合,其结果也更具实际意义。
NOTES
*通讯作者。