非线性与啁啾对艾里脉冲传输性质影响的研究

Study on the Influence of Nonlinearity and Chirp on Propagation Properties of Airy Pulse

摘要: 本文运用分步傅里叶法对初始啁啾与色散系数符号相同的情况进行数值模拟与分析，结果表明，啁啾的增大将进一步影响脉冲的展宽，影响脉冲传输质量。进一步研究了在自相位调制效应下，非线性系数对脉冲传输变化的影响，结果表明，在一定初始啁啾下，脉冲频谱主瓣强度有明显增大的趋势。

Abstract: In this paper, the Fractional Fourier method is used to simulate and analyze the case where the initial chirp and the symbol of the dispersion coefficient are the same. The results show that the increase in chirp will further affect the pulse broadening and the pulse transmission quality. The effect of the nonlinear coefficient on pulse transmission is further studied under the self-phase modulation effect. The results show that the intensity of the main lobe of the pulse spectrum tends to increase obviously under a certain initial chirp.

1. 引言

20世纪70年代末，Berry和Balazs从无势薛定谔方程求解了无衍射Airy波包 [1]。2007年，Sivilglou和Christodoulides在前者的基础上首次引入了有限能量的艾里光束的概念 [2]。自此以后，艾里光束引起了研究者们的广泛关注。艾里光束的传播特性主要包含三个：无衍射、自愈能力和横向自加速 [3] [4] [5]。这些独特的特性让艾里光束具有了光学粒子操纵 [6] [7] [8]、激光成丝 [9] [10]、非线性光学 [11]、产生自弯曲电子束 [12]、光学粒子捕获 [13] 等众多应用。

除了空间域的艾里光束，时域上随群速度变化而产生的加速度传播的有限能量艾里脉冲也被引入，与艾里光束相似，有限能量的艾里脉冲也具有其独特性质：近似无衍射、自愈、自加速(减速)。但相较于空间域上表现形式为光束弯曲的自加速，时域上艾里脉冲的自加速则表现为群速度的变化 [14]。对此的诸多研究引起了人们对艾里脉冲从线性到非线性领域传播的极大关注 [15] [16] [17]。如在克尔非线性条件下传播时，由自相位调制(SPM)和群速度色散(GVD)平衡条件形成孤子 [18] 以及高阶线性、非线性效应对艾里脉冲传输的影响等 [19]。

在过往的研究中，艾里脉冲的初始啁啾很容易被忽略，但啁啾对脉冲传播的影响很大，其对脉冲的影响主要作用在初始频谱上，频谱的改变将会影响艾里脉冲在线性和非线性中的传输。最近，有研究表明，考虑到GVD的作用，初始啁啾的符号在艾里脉冲传播中起着重要作用，艾里脉冲是否经历加速反转取决于初始啁啾和GVD的符号相同与否 [20]。其中，GVD和啁啾符号相同条件下的艾里脉冲传播，据我们所知，仍被研究的较少。本文将主要研究非线性与啁啾对艾里脉冲传输性质的影响。

2. 基本原理与理论模型

光脉冲在克尔介质中的传输可以用非线性薛定谔方程(NLSE)来描述，值得一提的是，NLSE方程可以用来描述皮秒量级的脉冲传输，当描述飞秒量级的光脉冲特性时，一些高阶效应参与者需要予以考虑，例如三阶色散(TOD)、拉曼效应和自陡(SS)等。我们对所有参量进行归一化处理，使得我们的输入峰值强度为1。时间量度T归一化入射脉冲初始宽度 $T_0$，传输距离Z通过色散长度 $L_D=T_0^2/{\beta }_2$ 作为长度尺度进行归一化测量，其中， ${\beta }_2$ 为群速度色散(GVD)系数。而后归一化非线性薛定谔方程表述为如下形式 [21]。

$i\frac{\partial U}{\partial Z}+\frac{1}{2}s\frac{{\partial }^{2}U}{\partial T^2}=0$ (1)

当考虑克尔非线性效应时，方程改写为：

$i\frac{\partial U}{\partial Z}+\frac{1}{2}s\frac{{\partial }^{2}U}{\partial T^2}+N^2{\left|U\right|}^{2}U=0$ (2)

这里的系数 $N=\sqrt{\gamma T_0^2{P}_0/\left|{\beta }_2\right|}$ 代表非线性的强度大小， $P_0$ 、 $\gamma$ 分别为入射脉冲的峰值功率和非线性指数。 $S=+1\left(S=-1\right)$ 代表正常(反常)群速度色散。

带初始啁啾的艾里脉冲表示为：

$U\left(T,Z=0\right)=Ai\left(T\right)\exp \left(\alpha T\right)\exp \left(-iC{T}^2\right)$ (3)

其中， $0<\alpha <1$ 为截断系数，需要说明的是艾里脉冲为多峰结构，所以艾里脉冲的主瓣宽度通常用作为时间尺度，C为初始啁啾。

3. 计算结果与讨论

3.1. 不同初始频率啁啾下脉冲的演化

不考虑三阶色散和光纤损耗，在线性区域传输时，我们对公式(3)做分步傅里叶法处理求解，利用Matlab模拟软件模拟出在正常色散(s = 1)下，在一个色散长度Z = 1内，不同啁啾值的脉冲时域演化图，为了便于观察比较，本文图中坐标数值我们均已做归一化处理，并且均在正常色散(s = 1)下进行。图1(a)所示，当初始啁啾C为0时，艾里脉冲保持其独特特性进行传输，引入啁啾值C，如图1(b)~(f)所示，艾里脉冲的传输演化过程发生了改变。图1(b)和图1(c)，当啁啾值较小时，初始啁啾艾里脉冲的演化过程类似于无初始啁啾的艾里脉冲，但传输仍受到了啁啾的影响。当初始啁啾值较大时(C ≥ 1)时，脉冲演化发生了明显改变，如图1(d)~(f)所示，我们分别取啁啾C = 1、2、5，从图中可以看出，在相同的色散长度内，相比于无初始啁啾(a)中的情况下，此时的艾里脉冲在传输过程中展宽程度加快，在C = 5时，发散更是明显。

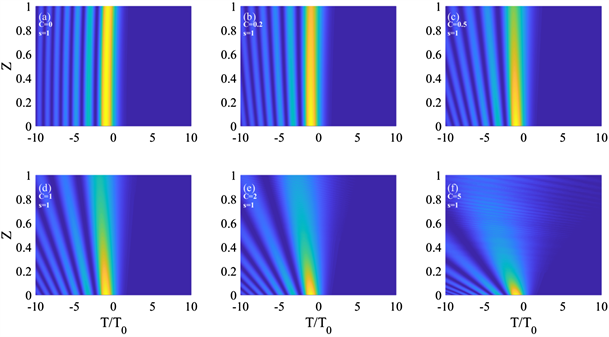
Figure 1. Pulse evolution process with different initial chirps C = (a) 0, (b) 0.2, (c) 0.5, (d) 1, (e) 2, (f) 5 when a = 0.05, s = 1, Z = 1

图1. a = 0.05，s = 1，Z = 1时，不同初始啁啾C = (a) 0, (b) 0.2, (c) 0.5, (d) 1, (e) 2, (f) 5的脉冲演化过程

为了更加直观表明初始啁啾对艾里脉冲传输演化的影响，我们对不同啁啾值的脉冲在传输距离为0.2个色散长度Z = 0.2时的情况进行了模拟，如图2所示，当Z = 0.2，C = 0时，艾里脉冲演化过程不发生改变，逐渐增大啁啾值，脉冲强度减弱，当增大到C = 5时，从图中可以明显观察到，脉冲此时已有脉冲展宽趋势，并且，啁啾值的改变同样引起了脉冲向前沿移动。通常，无初始啁啾的脉冲的色散感应频率啁啾会使得脉冲展宽，因此，我们可以引入一个符号相反的初始啁啾值进行补偿来减小展宽速度，甚至选取合适的啁啾值使得β₂C < 0，对脉冲起到压缩作用，提高脉冲传输质量。

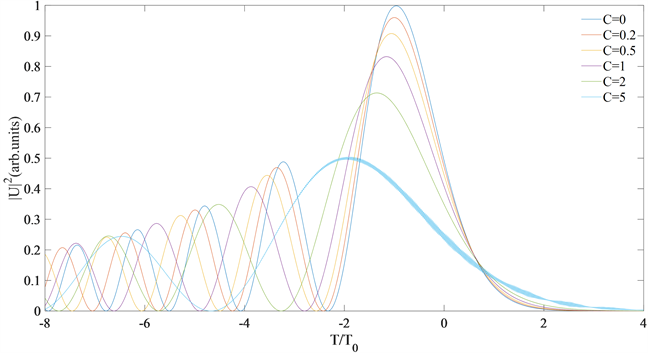
Figure 2. Pulse changes with different initial chirp values when Z = 0.2, s = 1

图2. Z = 0.2，s = 1时，不同初始啁啾值的脉冲变化

图3为相应的不同初始啁啾下脉冲的频谱图，其中， $v$ 和 $v_0$ 为相对频率和相对中心频率。从图中可以看出，啁啾值的大小对脉冲频谱分布影响很大。无初始啁啾时，频谱主瓣在中心频率处并且频谱分布均匀，当引人初始啁啾并且值比较小时，频谱分布发生变化，主瓣发生偏移，主瓣强度大于无啁啾情况，且强度随啁啾值的增加而减小。当啁啾值大于一定值时(图中C = 2)，主瓣偏移方向相反，且强度继续减小(小于无啁啾情况)。

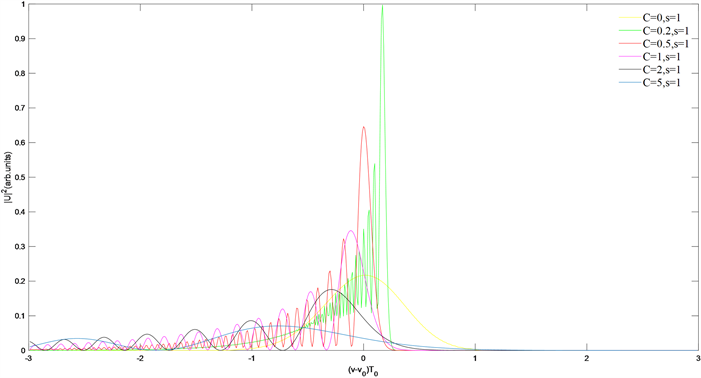
Figure 3. Spectrum diagram of pulses with different chirps

图3. 不同啁啾下脉冲的频谱图

上面提到，初始啁啾值的增大引起脉冲发散展宽程度的增大，因此，为了便于观察到不同截断系数对艾里脉冲传输的影响，我们选取初始啁啾C = 0.2的情况下进行模拟，如图4(a)所示，不考虑三阶色散及非线性的影响，我们发现，随截断系数a从0.05逐渐增大到0.3，艾里脉冲旁瓣数量以及旁瓣、主瓣强度减小，脉冲形随截断系数的增大逐渐失去其特征，更加接近于高斯脉冲，并且虽然不同截断系数脉冲的主瓣及旁瓣位置大体重合，但截断系数的变化仍轻微引起了峰值位置及脉宽的改变。由前面结果可知，不同初始啁啾下，频谱分布差异较大，为了便于观察，我们选取初始啁啾C = 2的情况进行模拟，如图4(b)所示。除啁啾变化引起的频谱分布移动外，从图中可以看出，截断系数的增大同样造成了频谱中旁瓣数量的减少，并且从图中可以观察到，频谱分布随截断系数的增大逐渐趋向高斯分布。

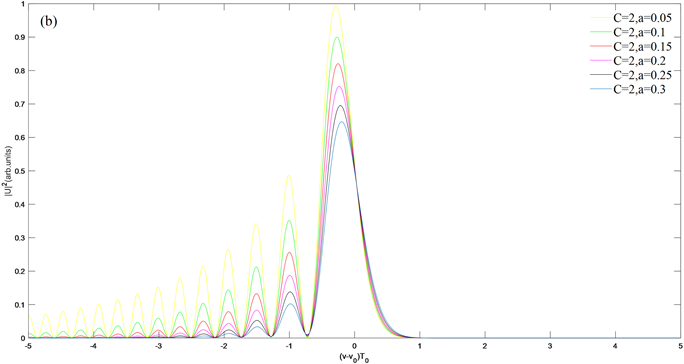
Figure 4. When Z = 2, (a) pulse changes with different truncation coefficients when C = 0.2, and (b) pulse spectrum diagram with different truncation coefficients when C = 2

图4. Z = 2，(a) C = 0.2时，不同截断系数的脉冲变化及(b) C = 2时，不同截断系数的脉冲频谱图

3.2. 自相位调制下的脉冲传输性质

以上情况均在正常色散(s = 1)的线性传输区下描述，当在克尔非线性条件下传输时，脉冲传输将发生截然不同的变化，下面，我们通过研究色散系数与初始啁啾符号相同的情况下，共同作用自相位调制(SPM)效应研究艾里脉冲的传输性质。

如图5所示，当初始啁啾C = 0.2的脉冲传输到两个色散长度时，可以看出，随非线性系数的增大，主瓣展宽，强度减弱并且峰值位置发生微小偏移，这可以通过SPM产生的在脉冲前沿附近红移而在后沿附近蓝移的新频率分量来解释：红移分量比蓝移分量传输的快，因此非线性项(SPM)的加入导致脉冲展宽速度加快。为了进一步研究SPM对脉冲的影响，不同非线性系数作用下脉冲的频谱图如图6所示。

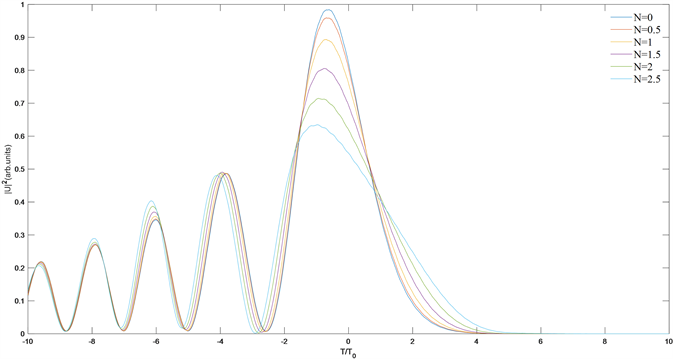
Figure 5. Pulse changes under different nonlinear actions when Z = 2, C = 0.2, a = 0.05

图5. Z = 2，C = 0.2，a = 0.05时，不同非线性作用下脉冲的变化

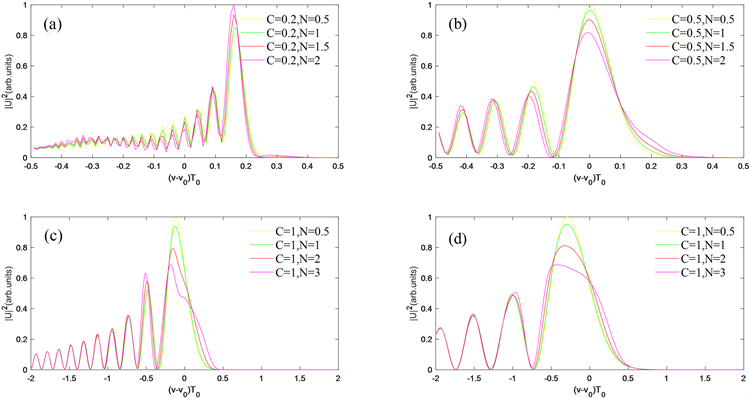
Figure 6. Spectrum diagram of different initial chirped pulses under different nonlinear effects when Z = 2, C = (a) 0.2, (b) 0.5, (c) 1, (d) 2

图6. Z = 2，C = (a) 0.2, (b) 0.5, (c) 1, (d) 2时，不同非线性效应下不同初始啁啾脉冲的频谱图

通常，SPM感应频率啁啾的时间相关性使得脉冲在两个不同点具有相同瞬时频率时，两点之间的相对相位差会发生干涉造成脉冲频谱的多峰结构，而在模拟中我们发现，相对于光强分布更加均匀的超高斯脉冲，艾里脉冲则更容易产生多峰结构，且随传输距离增加，这种结构更加明显，因此，为了便于较清晰的观察，我们取传输距离较小的两个色散长度处，对初始啁啾值较小和较大的情况分别模拟，如图6所示。在图6(b)~(d)中可以看出，脉冲主瓣强度随非线性系数的增大而减小，甚至在图6(c) C = 1，N = 3时，主瓣强度与第一旁瓣强度接近，除此，对比图6(a)~(d)可以发现，脉冲主瓣在时域中的展宽同样引起了频谱主瓣的展宽。相较于图6(b)~(d)，图6(a)则展示出了不一样的现象，当C = 0.2时，随非线性系数的增大，旁瓣强度减弱，但主瓣强度反而增大。

4. 结论

本文中，我们在忽略损耗、三阶色散及高阶非线性效应下，利用非线性薛定谔方程分别研究了初始啁啾、截断系数以及自相位调制对脉冲传输的影响，发现在正常色散区，初始啁啾及截断系数的增大将进一步影响脉冲时域的展宽和能量损失，在实际应用中，应予以减小避免。在非线性效应下，在较大啁啾的情况下，随非线性系数增大，频谱展宽程度增大，主瓣能量减小，但脉冲频谱在啁啾值较小时，表现出频谱主瓣峰值强度随非线性系数增加，呈迅速上升趋势。

NOTES

^*通讯作者。