1. 引言
在经典的合作博弈中,每个局中人都可以自由地与其他局中人合作,形成合作联盟,并获得相应的联盟收益。但在现实生活中,受到社会地位、文化背景、地理或物理等因素的影响,并非所有的联盟都可以形成。因此,联盟结构受到限制的合作博弈问题便得到了学者们的关注。Myerson [1] 首先提出了图限制博弈(简称图博弈)的概念:基于给定的图结构,每个节点均代表一个局中人,两个节点间的边则表示局中人间存在对等的双边关系。这种双边关系可以表示为局中人间的人际关系、制定的对等协议以及信息交流渠道等。在图博弈中,通常假定只有相互连通的局中人之间才能合作。借助Shapley值 [2],Myerson定义了图博弈的公平分配规则,并证明其是满足有效性和公平性的唯一解。这个解后来被称为Myerson值。众所周知,Shapley值是一个重要的合作博弈解概念,在自然科学和社会科学的众多领域均有其应用场景,例如以Shapley值作为清理河流污染或易腐品联合运输费用的成本分摊规则 [3] [4],以及以Shapley值作为产业集群企业的利益分配规则 [5] 等。Myerson值作为Shapley值的推广,其同样具有广泛的应用领域,例如网络微电网利润分配 [6]、碳减排责任分配 [7]、目标车头时距控制与双向自均衡车头时距控制 [8] 等。
自Myerson提出图博弈后,合作联盟受结构限制的合作博弈便得到了广泛的关注。Khmelnitskaya [9] 以及Khmelnitskaya等 [10] 研究了有具有向图结构的合作博弈,Myerson [11] 以及van den Nouweland等 [12] 将图博弈推广到了超图博弈,van den Brink等 [13] [14] 则对具有准许结构的合作博弈进行了研究。其中,准许结构可以用来描述上下级之间的控制关系,因此可以用有向图来进行表示。相对于无向图中的边,有向图中的有向边(弧)具有更加丰富的意义。除了控制关系外,有向边还可以描述先后关系以及路径关系等 [15] [16],Kalai和Zemel基于此提出网络流博弈 [17]。此模型目前被广泛应用于运输、通信、配送等领域的系统分析中。
上述的有向图博弈、准许博弈和网络流博弈均是基于不同的现实背景提出的博弈类型。受此启发,本文基于信息传递或物资运输的特性,提出了具有流结构的合作博弈(流博弈)。在流结构中,信息或物资只有从始发点发出并顺利抵达接收点,才能产生合作效益。因此,本文中假定,在有向图结构中,只有同时包含有效源点和有效汇点并且连通的联盟才是可行联盟,才能获得相应的联盟收益。基于这一假设,本文定义了流限制博弈,其赋予任意联盟其自主部分的收益,其中联盟的自主部分由联盟包含的所有可行联盟构成。借助Shapley值,本文定义了流博弈的一个分配规则——流值,并基于流博弈的有效性和流公平性完成了流值的公理刻画。与以往的研究相比,本文对网络流结构定义了相应的分配规则和公平性质等内容,论证了分配规则的合理性。同时本文的研究也填补了合作博弈在具有流结构限制上的研究空白。
本文的结构安排如下:第2节介绍了具有可转移效用的合作博弈(TU博弈)和有向图的相关概念。第3节定义了具有流结构的合作博弈及流值。第4节介绍了流博弈和流值在跨国公益物资运输问题中的应用,借助最小费用流构建了跨国物资运输博弈模型,并通过一个算例说明流值在公益物资运输费用的成本分中具有合理性。在第5节提供了结语。
2. TU博弈与有向图
一个具有可转移效用的合作博弈(TU博弈)通常用一个二元组
来表述,其中
是局中人集合,
是定义在局中人集合N上的特征函数且有
。任意的子集
称为一个联盟,
为联盟E能够获得的价值。为简便起见,用特征函数v代替
表示一个TU博弈。记
为所有局中人集合为N的博弈集合。
在合作博弈的众多分配规则中,Shapley值、等比例分配规则和按比例分配规则均是经典的解的概念。
定义2.1对于任意联盟
,称
为
维实向量空间
上的无异议基(无异议博弈) [18],如果对任意的联盟
有
;以及对联盟
有
。
根据无异议基,任意的博弈
可以表示为
。其中
为联盟
在
中的红利 [18]。
定义2.2 在博弈
中,局中人
的Shapley值 [2] 为
。
定义2.3 对任意TU博弈
,等比例分配规则分配给中局中人
的支付为
。
按比例分配以局中人在联盟中的权重为比例分配给他们相应的收益。
定义2.4 对任意TU博弈
,给定权重
,按比例分配规则分配给中局中人
的支付为
。
本文将用一个具有源点和汇点的有向图来表示一个流结构。令二元组
表示一个有向图,其中N是节点集合,每个节点对应合作博弈的一个局中人,
是流结构的弧集,其元素
是由i指向j的一条弧,表示信息(或货物)可行的流动方向。为简便起见,我们用符号D替代
表示一个有向图。符号
记为局中人
直接后继的集合;符号
为局中人i直接前驱的集合。此外,用
表示
在有向图D上的所有下级(或后继)的集合,即
当且仅当存在有限序列
使得
并且有
,成立。相应地,
记为局中人
在有向图D中所有上级(或前驱)的集合。此外,对任意
,令
。在有向图D中,记
为D中源点的集合,
为D中汇点的集合。记
和
分别为有效源点和有效汇点的集合。本文中,有效源点和有效汇点分别为信息或货物的实际发出地和目的地。若不存在
使得
或
,则称有向图D为无圈有向图。
3. 具有流结构的合作博弈
3.1. 流博弈和流值
我们称有向图D以及固定源点
和固定汇点
的结构是一个流结构,若D是一个无圈有向图且
和
均为非空。此外,我们称序列
为一条流,如果
且有
成立。
五元组
是一个具有流结构的TU博弈(简称流博弈),其中
是一个合作博弈,
是一个流结构。我们用符号
记作所有具有流博弈的集合。为简便起见,我们用符号
代替
表示一个流博弈。在流博弈中,只有包含完整流结构的合作联盟才是可行联盟。其经济意义为:信息或货物只有从发源地到达目的地才能产生经济效益。
为了更好地理解流博弈的合作特性,我们对可行联盟做进一步探索。
定义3.1在流博弈
中,子集
称为流结构
中的自主联盟,若对任意的
均有
,以及对于任意的
均有
同时成立。
实际上,流博弈的自主联盟就是可行联盟。令
为给定流结构
的所有自主联盟的集合,则由定义2.1可知
显然,自主联盟集是给定流博弈
的所有可行联盟的集合。
针对自主联盟集我们还有如下结论:任意两个自主联盟的并集仍然是自主联盟。
注3.1本文仅考虑连通图。
定理3.1设
是一个流博弈,则
,且对任意的
,均有
成立。
证明:由流结构的定义显然有
成立。令
,则
,且由定义3.1可知
且
,则
且
,故有
。
对任意联盟,其包含的局中人并非都能产生经济效益。因此,我们还需进一步对联盟中能够产生经济效益的局中人进行定义,以便确定联盟可以产生的价值。
定义3.2在流博弈
中,联盟
的自主部分为
。
由联盟自主部分的定义可知,任一联盟的所有自主子联盟构成了该联盟的自主部分,这部分的局中人正是该联盟能够产生经济效益的局中人的集合,即联盟的自主部分使得信息或货物能够从源点到达汇点,并在其中发挥了作用。
对于非自主联盟,其可以通过说服其他局中人的加入而形成自主联盟。对于非自主联盟成为自主联盟的过程,我们有如下可行流联盟的定义。
定义3.3设
是一个联盟,
是流结构
中E的可行流联盟,如果其满足:
i)
且
;
ii) 不存在
,使得
。
记
为联盟E在无圈流结构
中所有可行流联盟集的集合。显然
当且仅当每一个
都存在可行流联盟集
且
。使用可行流联盟的特征改写自主联盟集,即
或
。注意到对于任意非空联盟
都有
。
为了给出流博弈的一个解,我们首先基于流结构定义一个受限博弈。
定义3.4设
是一个流博弈,其流限制博弈
定义为:
定义3.4指出,在流限制博弈中,联盟仅能获得其自主部分相对应的收益。基于此受限博弈,可进一步给出该类博弈的一个解概念:
定义3.5映射
称为流值,其分配给任意的流博弈
一个支付向量为:
。
定义3.5说明,在流博弈中,流值分配给该博弈局中人其对应的流限制博弈的Shapley支付。
注意,在流博弈中,使用等比例分配的结果分别为:
。
使用等比例分配的结果分别为:
。
接下来我们通过一个例子来说明流博弈以及流值。
例3.1令
是一个4人流博弈,特征函数
,流结构为
,
,
。如图所示:
由定义3.1可知,该博弈的自主联盟集合为:
由定义3.4可得流限制博弈为:
结合定义3.5可计算流值为
。若有向图结构由图1所示的流结构
变为图2所示的流结构
且
和
保持不变,其中
,则新流博弈的自主联盟集合、流限制博弈以及流值分别为:
以及
。
由例3.1可知,在给定合作博弈特征函数的情况下,当流结构出现变化时,流博弈的支付结果也会相应地出现变动。下一节我们将流结构变化对流值的影响做进一步研究,并完成流值的公理刻画。
3.2. 公理刻画
令f是定义在
上的一个分配规则,其分配给任意的流博弈
一个支付向量
。
公理3.1 (有效性)对所有
,分配规则f满足有效性,如果有
。
有效性是指,大联盟中所有成员的支付之和等于大联盟的收益。换句话说,大联盟获得的收益将全部分配给其成员,不能多分也不能少分。
下面我们将证明流值满足有效性。
定理3.2流值
满足有效性。
证明:由Shapley值的有效性可知
,又由定理3.1可知
。
因此
。
公理3.2(流公平性)分配规则f是公平的,若对所有
以及
有:
其中
是常数以及
。
流公平性表明如果在同时包含h和j的自主联盟中删除局中人h与其直接后继j之间的关系,将会导致可行流联盟内局中人的流值增加或减少相同的数量。
在证明流值具有流公平性之前,我们先论证删除流结构的一条弧后对流结构带来的影响。
引理3.1对所有
和
则有
,其中
是流结构
所有自主联盟的集合。
证明:令
和
。
假设
,因为
,且
,因此
。
由上述引理可知,删除流结构中的弧会导致自主联盟变少。接下来我们用一个引理来说明,流结构的变化对某些自主联盟不会产生影响。
引理3.2对所有
和
,如果
且
,则
。
证明:令
和
。令
。如果对任意的
均有
,则由
的定义,
以及
且
可知
。
如果
,由假设
可知
。
由
,可知
且
。又由于
;
以及
的定义,可知
。
对于
但
的情况,可类似证明。
下面我们将证明流值满足流公平性。
定理3.3流值
满足流公平性。
证明:令博弈
,其中
是联盟
的无异议博弈,
是一常数,则
。
令
且
。对任意的
,由定义3.4可知,
,进而可知
。因此,我们仅考虑
的情况。
对于
,有
。
接下来证实以下事实:
i) 如果
,且
,则显然
。故
在流结构
中的自主部分与F在
中的自主部分相同。
因此
。
红利
。
ii) 引理3.2等价于若
,则
。因此
可以推导出
故
。
进而可以推导出以下事实:
iii) 由
的定义可知,对任意的
,如果
,则
。
iv) 对任意的
,如果
,则
当且仅当
。
v) 由事实(i)可知
且
。
因此对
以及
有
因此
。
综上,对任意的
,均有
最后,基于Shapley值的可加性,可知
其中
,成立。
借助定理3.2和3.3我们有如下流值的刻画定理。
定理3.4流值是
上满足流公平性和有效性的唯一解。
证明:由定理3.2和定理3.3可知,流值满足流公平性和有效性,下面证明唯一性。
令
。假设
和
是
上的两个公平分配规则。
通过递归
证明出
。
如果
,根据f的有效性可知
,因此
。
假设对所有
,有
成立。
现在考虑
。由流公平性可知
其中
且
。
由于
,故
。
因此
。
又因为
,因此有
又因为
和
均满足有效性,因此可知
,故
。
所以
,
,
。
因此
。
4. 应用:跨国公益物资运输问题
4.1. 模型建立
随着全球经济与科学技术的快速发展,贸易全球化已是大势所趋。全球疫情来临时,跨国公益物资运输是国际之间齐心协力合作抗击疫情的重要环节,充分彰显了人类命运共同体的现实意义与世界意义。本节以跨国公益物资运输问题为例,构建基于流结构的合作博弈模型,并针对跨国公益物资运输成本分摊的现实问题,介绍流值在公益物资运输中的应用。
首先,构建跨国公益物资运输合作博弈模型
。其中N为隶属于跨国公益物资运输涉及到的国家
的城市集合,城市之间的物资流通网络为
,
为隶属于物资供应国的城市集合,
为隶属于物资需求国的城市集合。流通网络
上的两个城市
之间若存在物资流通关系
,则其流通量记为
,最大流通量(容量)记为
,单位流量运价为
。
为确保将捐助的公益物资足量高效地送达物资需求国,假设当一条流路径无法满足运输需求时,则可以选择若干条由源点至汇点的流路径共同运输货物。
根据突发公共卫生事件的特征,在运输效率层面上,考虑流量最大化;在经济调度层面上,考虑运输费用最小化。基于以上两个因素,以文献 [19] 构建的最小费用流模型作为路径选择、路径流量分配以及运输费用产生的重要依据,该模型构建如下:
其中,f是网络
的流;
是流f的流量;
为联盟E在网络
的最大流;
为联盟E在跨国物资运输网络
中的最小费用流。第一条约束为容量约束,表示物资运输量不超过其通过道路的容量限制;第二条约束为流量平衡约束,表示物资的运输在由
至
的流路径上运行,且由源点发出的流量与抵达汇点的流量相等;第三条约束为流量和费用的非负约束,表示公益物资的运输是有效运输。
因此,任意联盟
需联合支付的费用为:
,其中,
为可行联盟特征函数,只有同时包含隶属于物资供应国的城市和物资需求国的城市的联盟才具有非零的效用。作为具有公益性的公益物资,其运输费用由所有参与国共同分摊。
下面是跨国公益物资运输以流值作为成本分摊规则的一个具体案例。
4.2. 算例分析
为隶属于国家
的国际城市集合,其中
。国家
和
、
和
、
和
、
和
以及
和
之间有公共国界,国家
和
之间无公共国界。流结构为
,其图形如图3所示。某国际卫生事件突发,此时城市1物资货源充足,城市4物资处于紧缺状态,急需城市1采用铁路运输的方式援助一批重要的公益物资运输至城市4以应对突发卫生事件,其运输的流路径需要途径城市2和3中的至少一个城市。以城市1作为流的源点,以城市4作为流的汇点,即
,自主联盟集为
。
假设各路段价格统一且
。单位流通量
。合作博弈特征函数为:若
且
,则
;否则,
。
由4.1节的最小费用流模型可知当
时,
;当
时,
;当
时,
。则联盟
运输公益物资的费用为
即
,以及其他情况
。
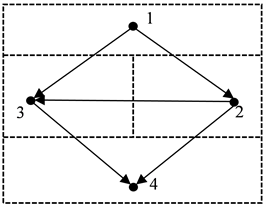
Figure 3. Transportation network diagram of transnational public welfare goods
图3. 跨国公益物资运输网络图
本例中各城市成本分摊结果如表1和图4所示:

Table 1. Cost allocation: flow value
表1. 成本分摊:流值
其中以节点的度作为按比例分配规则的权重
。
可以看出,在三种分配规则中,流值将最多的成本分摊给局中人1和局中人4,等比例分配使所有局中人分摊的成本平等,按比例分配将最多的成本分摊给局中人2和局中人3,局中人1和局中人4分摊同等的最小的成本。流值考虑到了流结构对成本分摊的影响。由于只有1和4同时加入联盟,自主联盟才能形成,所以1和4的流值大于3和4的流值,这体现了1作为源点以及4作为汇点在流结构中不可或缺的重要地位。且物资供应国与物资需求国对公益的积极程度较高,所以位于物资供应国与物资需求国的城市分摊的额度大于只是作为转运节点的城市。在联盟
中2对3具有转运作用,且2在
中的运输能力大于3在
中的运输能力,因此2的流值大于3的流值,这体现了分配规则的
公平。此外,若将
改为2,此时
,流值分配比例不变。因此流值具有合理性。
5. 结语
本文通过对具有流结构合作博弈的研究,利用Shapley值定义了流博弈的一个解——流值。随后,本文对流值进行了公理刻画,证明流值是满足有效性与流公平性的唯一解。最后,将此模型用于跨国公益物资的运输问题中,得到较为合理的成本分摊方案。
本文的研究表明,流值在有效性、流公平性、稳定性方面有很好的性质。本文所提出的具有流结构合作博弈模型适用于运输、通讯、工程规划等诸多实际应用场景,流值在其中的成本分摊与利润分配环节能够发挥作用。随着网络流与合作博弈理论和应用的不断发展,本文所提出的理论概念将在未来得到更广泛的应用。
致谢
对评审专家的仔细阅读和评审意见表示衷心感谢。
NOTES
*通讯作者。