1. 引言
近40年来,中国经济快速增长,城镇化快速发展,其主要原因是资源和要素的大量密集投入。改革开放后,中国中央政府通过连续五年规划实施区域发展战略,实现了中国经济的快速发展,这可以分为三个阶段。第一个时期是1978~1994年,区域发展战略不平衡,重点发展中国东部沿海地区。在这一时期,政府通过开放沿海城市,建立东部经济技术开发区,鼓励东部沿海地区率先发展,让一部分人、一部分地区富裕起来。这一战略极大地促进了中国的经济增长,同时也使东部地区与中西部地区的发展差距逐渐扩大。第二个时期是1995~2008年,是以缩小区域差距为目标的区域协调发展战略时期。实施西部大开发战略、东北老工业基地振兴战略、中部崛起战略,促进中西部地区发展。然而,随着经济的快速发展,城乡发展差距不断扩大,社会经济发展与资源利用、环境保护之间的矛盾日益突出。第三个时期是2009年至今,以均衡发展为目标的区域全面协调发展战略。区域协调发展不仅是解决发展不平衡不充分问题的内在要求,更是构建新发展格局的重要途经。党的十九大报告将“区域协调发展”列为建设现代化经济体系的重要内容,提出“建立更加有效的区域协调发展新机制”。改革开放以来,东部沿海地区快速发展,中国区域差距出现了持续扩大的趋势。在此背景下,党的十六届三中全会提出了“区域协调发展战略”。此后,各类资源开始向中西部地区引导和倾斜 [1] [2]。
新中国成立70年来,中国区域经济发展经历了由低水平的区域均衡发展到区域非均衡发展,再到强调区域协调发展的转变。展现了中国政府想要实现“共同富裕”目标的决心。目前东中西部地区之间的发展差异依旧较大,体现在经济、政治、生态等各个方面。当前和未来一段时期内,中国区域政策的重心仍是进一步促进区域协调发展,为高质量发展奠定基础 [3]。在完成2020年“全面消除绝对贫困”之后,原国务院扶贫办正式更名,挂牌为乡村振兴局。困扰我国千百年的绝对贫困问题得到了历史性解决,贫困治理的重心和难点由显性的绝对贫困转为隐形的相对贫困 [4]。服务对象从贫困地区、贫困人口,拓展到了所有农村、全体农民。未来,国家乡村振兴局的职能,也将因此进一步拓展。从脱贫攻坚战开始,各个省份,地级市的扶贫办都一套指标体系来确定扶助资源的分配方案。因此,本研究想基于当前对于中国相对贫困状况的研究成果,通过建立一个扶助资源分配数学模型,量化扶助决策效果,通过模型求解为决策层提供辅助资金分配策略,提高资源分配策略,促进区域均衡发展。
2. 文献综述
目前对区域发展的研究范围十分广泛,最基本地,文献研究已经从简单地注重经济发展变得更全面化,比如从经济与人类福祉的相关关系,经济可持续发展等角度出发。在区域发展与人类福祉之间的关系的研究文献中,它们与新古典主义中普遍将人类福利解释称国内生产总值,就业以及家庭收入等量化指标的行为区别开来。文献对福祉的概念不尽相同,主要是通过与诸如幸福,生活满意度,积极心理功能,人类发展,生活质量,平衡和亚里士多德的幸福观联系在一起。对该领域的文章,Maree Fudge [5] 等人为这一系列的文献提供了非常详尽的综述。
在可持续发展议题中,许多文献从空间均衡度出发,不同的文献对其定期不仅经济、资源、环境之间的关系出发,研究如何使得三者能够保持相对均衡,为决策者提供在有效利用资源,合理保护环境的同时促进经济长久发展的建议。Hongyan Shen等人指出了目前中国区域发展不协调所带来的不同程度的人口、经济、资源和环境的空间失衡,也即是人口和资源都过度集中于经济水平较好的区域,并且较快的经济发展会对环境的承载能力造成挑战。主基于此,他们构建了综合考虑经济、社会、资源、环境、生态等因素的评价指标体系,测度了中国290个地级市的空间平衡状况 [6]。
各个区域的空间不平衡意味着各类资源在区域之间分布不合理,其背后是各个区域之间巨大的发展差异。2015年10月29日,习近平在党的十八届五中全会第二次全体会议上的讲话鲜明提出了创新、协调、绿色、开放、共享的发展理念。2012年以来,中国的共享发展水平、创新发展水平、开放发展水平都得到了大幅提升,绿色发展水平有一定提高,而协调发展水平则出现了较大幅度的下降 [7]。其中区域协调发展也就是意味着区域均衡发展,是中国目前急需解决的重大问题之一。此外,区域均衡问题是区域发展问题中非常重要的一部分。
许多文献进行不同层次的区域不平等评估指标的建立。一部分文献将地区间经济增长的差距视作区域不平等的基本来源 [8],研究主要涉及三个“如何”问题:如何空间不平衡的出现,空间不平衡如何演变,以及空间不平衡如何消除。1965年,威廉姆森观察到区域经济增长不平衡呈倒U型分布 [9]。Pan等人基于厦门-漳州-泉州城市群区的可见光红外成像辐射仪夜间光影像数据和多维社会经济数据,采用主成分分析(PCA)和泰尔指数分解方法建立了综合贫困指数(IPI)和区域不平等指数 [10]。Shu Hui等人考虑到区域经济和生态效益指标分布差异结合地区差异性,建立了一个综合基尼系数衡量中国区域均衡发展程度 [11]。Li和Wei采用变异系数(CV)、基尼系数和泰尔指数这三个统计指标探讨了中国的区域间、省际和区域内的不平衡 [12]。Tirado等人基于地区GDP数据,计算人口加权变异系数(WCV)来研究西班牙十年以来的区域不均衡程度演变过程 [13]。
也有许多文献对国内外的区域差异来源,区域发展中的均衡发展的影响变量进行了各类的研究,并且提出相应的政策性建议。Su Yi等人使用面板门槛回归模型进行定量分析,发现区域科技创新对较低经济水平的地区的可持续发展有明显促进作用 [14]。孙荣臻使用方差分解法,基于新古典主义区域空间均衡理论,研究了我国东中西部区域内和区域间的经济差距来源,为推动区域均衡发展提供了政策性建议 [15]。Ren Ding研究同一货币政策下区域经济发展的分化,证明货币政策适应区域实际对平衡区域经济发展具有重要意义 [16]。
针对区域发展不均衡的问题,急需通过外部有效的政策支持与经济援助来改变现状。目前也有一系列的研究探索了资源扶助方案。Lei Chen等人使用逆数据包络法,根据实际的需求制定促进空间平衡的具体到金额的投资方案 [17];Lijing Tang等人通过从可持续发展角度,构建县域在农业和非农业用地之间土地资源配置效率的评估模型,并以一个县级市案例,阐述了如果采取对应政策提高配置效率,从而优化土地资源配置,促进区域均衡发展 [18]。赵扶扬等人研究东西部间建设用地指标分配对我国经济增长,即“效率方面”和区域发展均衡,即“公平”两方面的影响,他们通过量化空间模型,证明了中国当前土地配置策略能够在“效率”和“公平”上找到了一个良好的平衡点,既实现了GDP和总福利的显著提升,又明显缩小了区域的人均收入差距。为了进一步促进我国的区域均衡发展,他们在生产要素配置优化,以及产品和服务的流通方面提出了具体的政策建议 [19]。
综上可以发现目前大部分关于区域均衡的问题都处于区域经济学或实证分析领域,多采用实证分析方法,并运用一定的计量经济学模型。很少有文献从运筹学角度建立数学规划模型来研究如何通过资源的合理分配,进而有效扶助欠发达地区的经济增长。本文将在第3章提出一个以最小化区域间发展差异的单目标数学规划模型,在第4章节中介绍了一个通用的分数模型的求解方法。本文的研究成果未来可以应用于实际的资源分配场景中,基于待分配对象具体经济情况来针对性地确定定量的资源分配方案,提高资源分配效率和资源扶助效率,促进地区区域经济均衡发展,进而促进区域的可持续发展。
3. 建立模型
基于上述提到的问题,本文旨在建立了一个研究扶助资源分配的单目标数学规划模型,能够产生理想的扶助资源分配方案,将有限的资源可以通过有效且公平的方式分配给目标地区。不同于普通资源分配问题中仅仅考虑将现有的资源进行下发,本模型引入扶助资源效用参数
来衡量扶助资源对于被援助地区在经济发展上产生的影响,以最小化扶助资源分配后被援助地区间发展差异水平为模型目标。
假设当前有总额为b的可量化扶助资源需要分配给地区J。地区J下有多个子区域。用
来量化子区域j当前的发展水平。如该地区的农村可支配收入与人均GDP水平。
假设每个地区需要的扶助资金
是相互独立的且与该地区当前经济发展水平呈正相关。引入0~1变量
表示对地区的资助情况,若取值为1表示资助,反之不资助。因此,对于所有地区的分配的资助金额应该满足下式:
其中,
为扶助资金的使用比例下限。取值可以按照实际要求确定。
不同地区获得资助后,经济发展水平的增速不一定相同,如上述使用
表示。用连续变量
表示在扶助资源分配后地区j的经济发展水平。由此可以获得
的计算公式:
通过分配扶助资源降低地区发展差异的同时,也应该建立约束来保证地区的整体发展水平基数,式子如下:
在统计学中,变异系数是衡量数值差异程度的代表性指标,且被排除了量纲的影响。本文研究的问题为通过有效的资源分配方案使得扶助资源生效后各个地区的发展水平差异能够有所降低。因此可以通过构建基于分配后各个地区的发展状况
建立变异系数指标,表达式如下:
其中,
为各地区被援助后发展状况
的均值。
综上,以被扶助资源分配后,得到具体模型如下:
s.t
(1)
(2)
(3)
(4)
(5)
(6)
目标函数为最小化地区经济发展水平差异。约束(1)为扶助资源分配后各个地区发展水平计算式;约束(2)限制了扶助资源能后实现的区域最低发展水平;约束(3)与约束(4)规定了扶助资源的利用率应该处于
之间;约束(5),(6)为决策变量的数值类型约束。
4. 求解方法
在第3章中,本研究建立的数学规划模型为单目标分数规划模型。本章节整理了当前的分数规划模型的求解研究,汇总得到一种单目标分数规划模型的求解方法。
设有问题P,构造如下:
s.t.
同时有问题
,构造如下:
s.t.
设
。当且仅当
为
的最优解时(此时需满足
),
为问题P的最优解 [20]。因此为了能够找到
,首先需要找到
,现在引入定理1 [21],如下:
定理1:设
为问题P的最优解,且
,那么
1) 当且仅当
时,有
2) 当且仅当
时,有
3) 当且仅当
时,有
基于定理1,可以使用牛顿法 [22] 来确定
。其主要思想是生成一系列递增的
作为下界来逼近
,迭代算法的具体步骤如下:
输入:一个连续且单调递减的凸函数
,任意的
满足
。存在可行解解集X的问题P。令
,进入步骤1
步骤1:令
,其中
;
步骤2:若
,则令
,运算结束;
步骤3:若
,则令
,返回步骤1;
输出:此时
即为问题P的最优目标函数值,
为问题P的最优解,算法结束。
基于上述方法,将问题P转化成问题
,针对
进行迭代求解,得到
与
,即可得到单目标分数规划问题P的解及最优目标函数值。
5. 数值实验
在本章节中,将对模型中的具体参数进行合理的假设,并基于现实的县市经济数据进行案例研究,通过本文数据模型确定具体的资源分配方案。
本章节的相关数据来源于《2020年甘肃省统计年鉴》中甘肃省86个县(最小行政单元)的经济发展数据指标(相关数据缺失的县已被略去)。在本次实验中,使用各县的农村人均可支配收入作为地区发展水平
的量化指标,这也是中国脱贫攻坚战中衡量地区扶贫进展的重要指标,方差为0.4413。此外假设一个地区需要的扶助资金数额
与该地区的GDP成正相关,在本数值实验中,设
。进一步地,假设本数值实验中的可分配扶助资金计算表达式如下:
其中
衡量扶助资金的紧缺性,在本数值实验中
。
基于各个地区的经济发展状况
,可以按照合理的贫困标准线对各县市的贫困状况进行分类。本数值试验中的分类标准基于2019年程蹊等人关于中国的贫困线标准的研究 [23]。第一个分界点为10,609.2,为全国人均可支配收入中位数的40%,这是中国在摆脱绝对贫困问题后,一个合理的用来衡量相对贫困状况的标准线。例如,农村人均可支配收入在(0, 10,609.2)区间的县市,在本研究问题中即属于第1类。第二个分界点为15,366.5,为全国人均可支配收入的50%。类似地,农村人均可支配收入在(10,609.2, 15,366.5)区间、(15,366.5, +∞)区间的县市分别属于第2类和第三类。基于以上两个分界点,可以将甘肃省86个县市分成三个主要的贫困等级。
在此基础上,假设经济发展水平较差的县市在得到资助之后能够产生的增速较大。例如,若第1类中的子区域获得资助,资源生效后其农村人均可支配收入能获得7%的增速。而相同情况下,处于第2类中的子区域经济水平相对第1类中的更好,获得资助时可以获得5%的增速。下表1列出了各个类别下的子区域数量,以及不同类别下子区域获得资助后能够得到的增速:

Table 1. Poverty classifications of counties and cities in Gansu province
表1. 甘肃省各县市贫困水平分类情况
通过设置增长速率约束中的下限,可以通过本文的模型获得一系列的资源分配方案。不同的分配方案可以帮助地区实现不同程度的区域均衡发展,具体的方案效果见下表2。

Table 2. The effects of different assistance schemes
表2. 资源分配方案的效果
基于实验结果,下文分析了不同的方案及其方案的实际效果特点,并给出了一定管理上的建议:
· 甘肃各县级市经济发展水平的原始方差为0.4413。在本次数值实验中,得到的4个不同的资源分配方案,均可以不同程度地促进地区发展均衡。其中方案1可以将子区域的经济水平方差降低至0.4073,降低幅度达8.35%;
· 通过设置增长速率约束中的下限,可以发现扶助资金分配方案能帮助地区在保持一定整体发展均速的同时,促进区域发展均衡性。但两者为反相关关系,如图1,即一个资源分配方案最终能够实现的子区域间经济水平差异越小,其对子区域的整体发展增速的提升作用也越小;
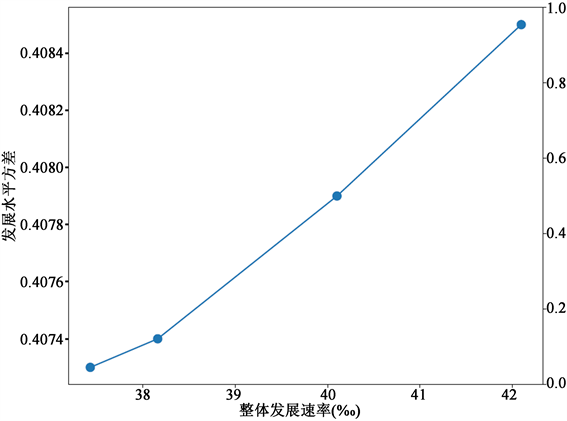
Figure 1. Trade-off curve between coefficient of variance and overall development rate
图1. 发展水平方差与整体发展速率的折线图
· 基于第2点的结论,可以总结到若子区域间均衡发展视为最重要的目标时,得到方案的资金利用率也会较低,因为此时会通过放弃资助部分经济发展水平较高的子区域的方式实现均衡。此时针对未被利用的部分资金,可以通过本模型确定进一步的分配方案,将该部分的剩余资源优先分配给经济发展较差的地区,进而进一步缩小各区域间的经济发展水平。
6. 总结
本文基于单目标数学规划模型,提出了一种可以确定区域内扶助资源定量分配方案的研究方法。本模型以最小化区域发展差异为模型目标,并结合区域整体发展水平约束。基于本模型产生的资源分配方案可以促进子区域发展均衡,并帮助被援助的目标地区提升整体发展水平。针对该模型本文也整理得到了单目标分数规划模型的求解方法,通过该方法可以得到单目标模型的最优解。本文后续通过数值实验证明了模型的有效性,基于实际经济数据,通过调整不同的区域整体发展水平下限要求,得到了一系列的不同效果的资源分配方法。进一步地,本文基于各方案的特点给出了管理实践上的建议。综上,面对实际非盈利性组织中的可量化扶助资源,均可应用本文模型来制定可以促进区域均衡协调发展的资源分配方案。