一类多参数不确定切换系统的分布鲁棒最优控制

Distributionally Robust Optimal Control of a Class of Switched Systems with Multiple Uncertain Parameters

摘要: 分布鲁棒优化结合了传统随机规划和鲁棒优化的优点，成为了近些年来解决含有不确定信息的优化问题的研究热点。结合分布鲁棒优化的特点，本文考虑了不确定参数的分布是未知，但一阶矩和二阶矩已知的切换系统分布鲁棒最优控制问题。该问题本质上是一个极小极大最优控制问题。本文利用控制参数化将原问题近似为有限维的参量最优控制问题，并将内层问题和外层问题分别求解。内层用非线性规划方法进行求解，外层则通过构造竞争粒子群算法进行求解。并以一类微生物批式流加发酵分布鲁棒最优控制问题作为实例验证了算法的有效性。

Abstract: Distributionally robust programming has become a hotspot to solve optimization problems with uncertain information in recent years, which combines the advantages of traditional stochastic programming with robust optimization. Motivated by the feature of distributionally robust pro-gramming, this paper considers a distributionally robust optimal control problem of switched sys-tems with uncertain parameters, in which the exact distributions of the uncertain parameters are unknown but the information of the first-order moment and the second-order moment are known. The problem is a minimax optimal control problem in essential, which is approximated by a fi-nite-dimensional parameter optimization problem via the control parametrization method. Then, we solve inner subproblem and outer subproblem separately, where the inner subproblem is solved by the nonlinear programming technique and the outer subproblem is solved by a competi-tive particle swarm optimization algorithm. Finally, the effectiveness of algorithm is verified by a distributionally robust optimal control problem of a microbialfed-batch process.

1. 引言

传统的随机规划大多研究的是随机变量分布信息完全已知的情况或者不确定性被处理成分布已知的随机变量 [1] [2] [3]。但在实际中不确定性的分布函数很难完全已知或者只知道分布部分信息。而分布鲁棒优化只是对随机变量的未知分布提出了限制约束，并还沿用了鲁棒优化的最差期望性能，在计算方面也较为容易实现。因此，对分布鲁棒优化的研究成为运筹学领域研究的热点。

常见的分布鲁棒优化问题的数学形式为

$\underset{x\in \mathcal{X}}{\min }\underset{F\in \mathcal{F}}{\max }{\mathbb{E}}_F\left[f\left(x,\xi \right)\right]$ (1)

其中， ${\mathbb{E}}_F[\cdot ]$ 表示在分布F下关于 $\xi$ 取期望， $\mathcal{F}$ 是分布不确定集。早在1958年，Scarf为解决一些简单的库存问题提出了分布鲁棒优化模型 [4]。对于不确定集的模糊性的处理常用的方法是利用分布的矩信息。例如，Bertsimas和Popescu用期望和方差定义分布集合 [5]，Bertsimas、Natarajan和Teo用边缘矩已知定义分布集合 [6] [7]，Delage和Ye用不确定参数的均值、协方差矩阵构造分布不确定集合 [8]，Wiesemann、Kuhn和Sim用概率约束和矩约束构造了不确定集 [9]。除此之外还有其他构造不确定集合的方法。如Alison用K-L散度 [10]，Kuhn用wasserstein距离来构造不确定集 [11]。在2016年，叶剑雄等人受分布鲁棒优化的启发，考虑了一类不确定参数自治切换系统的分布鲁棒最优控制问题 [12]，其中不确定参数的分布是未知的，但一阶矩和二阶矩已知，并以最差期望性能为目标性能。

本文将以文献 [12] 的模型为基础，进一步考虑多参数不确定切换系统的分布鲁棒最优控制问题。已知不确定参数的一阶矩和二阶矩信息，以一阶矩和二阶矩为约束，通过最小化不确定集中的所有分布的最坏情况期望为目标性能，建立分布鲁棒最优控制模型，重点考虑了离散分布情形的问题。该问题是一个min-max问题，其内层优化是求解最差期望性能的分布，外层为具有动力系统约束的非线性最优控制问题。本文运用非线性规划方法求解内层问题，再利用竞争粒子群对外层问题进行迭代计算。最后，以一类微生物批式流加发酵的分布鲁棒最优控制问题作为实例，阐述了多参数不确定切换系统的分布鲁棒最优控制问题的应用，并验证了所构造算法的有效性。

2. 问题描述

考虑如下带有不确定参数的切换系统：

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right),v\left(t\right),p\right),\\ x\left(0\right)=x^0,\end{array}$ (2)

这里， $x\in R^{n_x}$ 是状态向量， $u\left(t\right)\in R^{n_u}$ 是连续控制函数， $v\left(t\right)\in \left\{v^1,v^2,\cdots ,v^m\right\}$ 为离散控制， $p\in R^{n_p}$ 是不确定参数。一般情况下， $p$ 被假设为确定的，但这一假设在许多实际问题中并不成立。本文假设对于 $p$ 只知道它的一些分布信息，进而考虑如下切换系统的分布鲁棒最优控制问题：

$\begin{array}{l}(DROCP)\underset{u,v}{\min }\underset{F}{\max }J\left(u,F\right)\triangleq {\mathbb{E}}_{F}h\left(x\left(t_f;u,v,p\right)\right)\\ \text{s}\text{.t}\text{.}\stackrel{\dot{}}{x}\left(t\right)=f\left(x,u,v,p\right),t\in \left[0,t_f\right],x\left(0\right)=x^0,\\ p~F\in \mathcal{F}\left(\mu ,\Sigma \right)=\left\{F:{\mathbb{E}}_F\left(p\right)=\mu ,{\mathbb{E}}_F\left(p-\mu \right){\left(p-\mu \right)}^{\top }=\Sigma \right\},\\ u\left(t\right)\in U\subset R^{n_u},v\left(t\right)\in \left\{v^1,v^2,\cdots ,v^m\right\}.\end{array}$ (3)

这里，U是凸紧集且 $U\subset R^{n_u}$，F是不确定参数 $p$ 的一个分布，该分布下 $p$ 的一阶矩和二阶矩分别为 $\mu =\left({\mu }_1,{\mu }_2,\cdots ,{\mu }_{n_p}\right)$ 和 $\Sigma =\left({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_{n_p}\right)$。

对上述问题，本文考虑离散分布的情形。设 $p:=\left(p_1,p_2,\cdots ,p_{n_p}\right)$，其中分量 $p_i$ 有 $l_i$ 种可能取值，分别为 $p_i^1,p_i^2,\cdots ,p_i^{l_i},i=1,2,\cdots ,n_p$。并令 $\mathbb{P}\left(p_i=p_i^j\right)=q_i^j$， $i=1,2,\cdots ,n_p$， $j=1,2,\cdots ,l_i$。令 $p^k=\left(p_1^{j_1},p_2^{j_2},\cdots ,p_{n_p}^{j_{n_p}}\right)$ 为参数向量 $p$ 的第k种可能取值，由于 $p$ 的各分量分别有 $l_1,l_2,\cdots ,l_{n_p}$ 种取值，可知 $k\in \left\{1,2,\cdots ,{\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{l}_i}\right\}$，且 $\mathbb{P}\left(p=p^k\right)={\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{q}_i^{j_i}}$。设 $q:=\left(q_1^1,q_1^2,\cdots ,q_1^{l_1},\cdots ,q_{n_p}^1,q_{n_p}^2,\cdots ,q_{n_p}^{l_{n_p}}\right)$。问题(DROCP)可以等价于如下问题(DROCP1)：

$\begin{array}{l}(DROCP1)\underset{u,v}{\min }\underset{q}{\max }{\displaystyle \underset{j_1=1}{\overset{l_1}{\sum }}{\displaystyle \underset{j_2=1}{\overset{l_2}{\sum }}\cdots }{\displaystyle \underset{j_{n_p}=1}{\overset{l_{n_p}}{\sum }}\left({\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{q}_i^{j_i}}\right)\cdot h\left(x\left(t_f;u,v,p^k\right)\right)}}\\ \text{s}\text{.t}\text{.}{\stackrel{\dot{}}{x}}^k\left(t\right)=f\left(x,u,v,p^k\right),t\in \left[0,t_f\right],x\left(0\right)=x^0,\\ u\in U,v\left(t\right)\in \left\{v^1,v^2,\cdots ,v^m\right\},\\ {\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}=1,}\\ {\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}{p}_i^{j_i}={\mu }_i,}\end{array}$ (4)

$\begin{array}{l}{\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}{\left(p_i^{j_i}\right)}^2}={\left({\mu }_i\right)}^2+{\left({\sigma }_i\right)}^2,\\ q_i^j\ge 0,j=1,2,\cdots ,l_i,\\ i=1,2,\cdots ,n_p.\end{array}$

为了将控制函数 $u\left(t\right)$ 参数化，令 $0=t_0<t_1<\cdots <t_n=t_f$。利用分段常值函数来近似控制函数 $u\left(t\right)$，即

$u\left(t\right)={\displaystyle \underset{s=1}{\overset{n}{\sum }}{\eta }_s}{\chi }_{I_s}\left(t\right),t\in \left[0,t_f\right]$ (5)

这里， ${\eta }_s=\left({\eta }_s^1,{\eta }_s^2,\cdots ,{\eta }_s^{n_u}\right)\in U$， $I_s=\left[t_{s-1},t_s\right),s=1,2,\cdots ,n$， ${\chi }_I$ 是集合I的示性函数，即

${\chi }_I=\{\begin{array}{ll}1,\hfill & t\in I,\hfill \\ 0,\hfill & 其他,\hfill \end{array}$ (6)

定义 $\eta =\left({\eta }_1,{\eta }_2,\cdots ,{\eta }_n\right)$， $\mathcal{V}={\displaystyle \underset{s=1}{\overset{n}{\prod }}U}$。令 $x\left(t;\eta ,v,p^k\right)$ 是对应于 $(\eta ,v,p^k)$ 的系统(2)的解。则问题(DROCP1)可近似为如下有限维的参量最优控制问题(DROCP2)：

$\begin{array}{l}(DROCP2)\underset{\eta ,v}{\min }\underset{q}{\max }{\displaystyle \underset{j_1=1}{\overset{l_1}{\sum }}{\displaystyle \underset{j_2=1}{\overset{l_2}{\sum }}\cdots }{\displaystyle \underset{j_{n_p}=1}{\overset{l_{n_p}}{\sum }}\left({\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{q}_i^{j_i}}\right)\cdot h\left(x\left(t_f;\eta ,v,p^k\right)\right)}}\\ \text{s}\text{.t}\text{.}{\stackrel{\dot{}}{x}}^k\left(t\right)=f\left(x,\eta ,v,p^k\right),t\in \left[0,t_f\right],x\left(0\right)=x^0,\\ \eta \in \mathcal{V},v\left(t\right)\in \left\{v^1,v^2,\cdots ,v^m\right\},\\ {\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}=1,}\\ {\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}{p}_i^{j_i}={\mu }_i,}\end{array}$ (7)

$\begin{array}{l}{\displaystyle \underset{j_i=1}{\overset{l_i}{\sum }}{q}_i^{j_i}{\left(p_i^{j_i}\right)}^2={\left({\mu }_i\right)}^2+{\left({\sigma }_i\right)}^2,}\\ q_i^j\ge 0,j=1,2,\cdots ,l_i,\\ i=1,2,\cdots ,n_p.\end{array}$

3. 计算方法

显然，问题(DROCP2)是一个min-max问题，其内层关于 $q$ 的优化问题是约束线性，目标函数为多项式结构，相对容易求解，但其外层为具有动力系统约束的非线性最优控制问题，其求解难度相对较大。为充分利用内层优化相对容易求解的特点，本文将内层问题与外层问题分别求解。其中，内层问题利用非线性规划方法进行求解，外层问题则通过构造竞争粒子群 [13] 进行求解。

为叙述方便，令 $J\left(\eta \right)=\underset{q}{\max }{\displaystyle \underset{j_1=1}{\overset{l_1}{\sum }}{\displaystyle \underset{j_2=1}{\overset{l_2}{\sum }}\cdots }{\displaystyle \underset{j_{n_p}=1}{\overset{l_{n_p}}{\sum }}\left({\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{q}_i^{j_i}}\right)\cdot h\left(x\left(t_f;\eta ,v,p^k\right)\right)}}$。对于给定的 $\eta$，先将 $J\left(\eta \right)$ 转化成 $\tilde{J}\left(\eta \right)=-\underset{q}{\min }{\displaystyle \underset{j_1=1}{\overset{l_1}{\sum }}{\displaystyle \underset{j_2=1}{\overset{l_2}{\sum }}\cdots }{\displaystyle \underset{j_{n_p}=1}{\overset{l_{n_p}}{\sum }}\left({\displaystyle \underset{i=1}{\overset{n_p}{\prod }}{q}_i^{j_i}}\right)\cdot h\left(x\left(t_f;\eta ,v,p^k\right)\right)}}$，再通过Python里的minimize函数求解内层问题 $\tilde{J}\left(\eta \right)$，并给出其估计值。然后，构造如下竞争粒子群算法来计算问题(DROCP2)的外层问题的最优解。

算法3.1

步骤1 设置种群中粒子总数M。k是迭代次数，令 $k=1$。

步骤2 随机产生一个初始种群 $\left\{{\eta }_i\left(1\right)|{\eta }_i\left(1\right)\in U,i=1,2,\cdots ,M\right\}$。设置初始速度 $v_i\left(1\right)=0.001\cdot {\eta }_i\left(1\right)$， $i=1,2,\cdots ,M$。设置最大迭代数 $N_{ite}$。

步骤3 当 $k\le N_{ite}+1$ 时，记 $\Lambda \left(k\right)=\left\{{\eta }_i\left(k\right)|i=1,2,\cdots ,M\right\}$。若 $k=1$，则计算性能指标 $\tilde{J}\left({\eta }_i\left(k\right)\right)$， $i=1,2,\cdots ,M$。否则，计算性能指标 $\tilde{J}\left({\eta }_i\left(k\right)\right),i=1,2,\cdots ,\frac{2\cdot M}{3}$。

步骤4 计算 $\bar{\eta }:=\frac{1}{M}{\displaystyle \underset{i=1}{\overset{M}{\sum }}{\eta }_i\left(k\right)}$ 和 ${\eta }_{best}:=\underset{1\le i\le M}{\arg }\min \tilde{J}\left({\eta }_i\left(k\right)\right)$。

步骤5 当 $j=1,2,\cdots ,\frac{M}{3}$ 时，依次执行6~9。

步骤6 从 $\Lambda \left(k\right)$ 中任意选取三个粒子，分别记为 ${\eta }^{j_1},{\eta }^{j_2},{\eta }^{j_3}$，并记 $\Lambda \left(k\right):=\Lambda \left(k\right)$ \ $\left\{{\eta }^{j_1},{\eta }^{j_2},{\eta }^{j_3}\right\}$。

步骤7 假设 $\tilde{J}\left({\eta }^{j_1}\right)\le \tilde{J}\left({\eta }^{j_2}\right)\le \tilde{J}\left({\eta }^{j_3}\right)$，令 ${\eta }_j^w\left(k\right):={\eta }^{j_1}$， ${\eta }_j^{l1}\left(k\right):={\eta }^{j_2}$， ${\eta }_j^{l2}\left(k\right):={\eta }^{j_3}$。这里， ${\eta }_j^w\left(k\right)$， ${\eta }_j^{l1}\left(k\right)$， ${\eta }_j^{l2}\left(k\right)$ 分别表示第j轮竞争中的获胜者和两个失败者。

步骤8 根据位置和速度更新公式更新 ${\eta }_j^a\left(k\right)\left(a=l1,l2\right)$。其中，位置更新公式和速度更新公式分别如下：

${\eta }_j^a\left(k+1\right)={\eta }_j^a\left(k\right)+V_j^a\left(k+1\right),\left(a=l1,l2\right).$ (8)

$\begin{array}{l}{V}_j^a\left(k+1\right)=w\left(k\right)\cdot V_j^a\left(k\right)+R_{1,j}^a\left(k\right)\left({\eta }_j^w\left(k\right)-{\eta }_j^a\left(k\right)\right)+R_{2,j}^a\left(k\right){\varphi }_1\left(\overline{\eta \left(k\right)}-{\eta }_j^a\left(k\right)\right)\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}+R_{3,j}^a\left(k\right)\varphi \left({\eta }_{best}-{\eta }_j^a\left(k\right)\right),\left(a=l1,l2\right).\end{array}$ (9)

这里 ${\varphi }_1$ 表示 $\overline{\eta \left(k\right)}$ 的影响参数， ${\varphi }_2$ 表示 ${\eta }_{best}$ 的影响参数。 $R_{i,j}^a,i=1,2,3$ 是在第k次迭代的第j轮竞争中(0, 1)区间上不同的随机数。

步骤9 记 ${\eta }_j\left(k+1\right):={\eta }_j^{l1}\left(k\right)$， ${\eta }_{\frac{M}{3}+j}\left(k+1\right):={\eta }_j^{l2}\left(k\right)$， ${\eta }_{\frac{2\cdot M}{3}+j}\left(k+1\right):={\eta }_j^w\left(k\right)$， $\tilde{J}\left({\eta }_{\frac{2\cdot M}{3}+j}\left(k+1\right)\right):=\tilde{J}\left({\eta }_j^w\right)$。

步骤10 $k=k+1$。

4. 数值算例

本节以一类微生物批式流加发酵模型为例，对上述算法进行验证。批式流加发酵过程是指在开始时往发酵罐注入一定的微生物和底物搅拌均匀后培养一段时间，之后为了使底物浓度和发酵液的营养物浓度保持在一定范围内，将底物分批次灌入发酵罐中。设 $x:=\left(x_1,x_2,x_3\right)=\left(X,S,V\right)\in R_{+}^3$ 为连续状态变量。其中，X是生物量浓度(g/L)，S是底物浓度(g/L)以及V是发酵液体积(L)。 $v\left(t\right)$ 表示底物的流加速度(L/h)， $v\left(t\right)\in \left\{0,0.02\right\}$。假设整个批式流加发酵时间区间为 $\left[0,t_f\right]$。根据微生物生长特征，将整个发酵过程分为N个阶段，即 $0=t_0<t_1<\cdots <t_N=t_f$，这里N是一个正整数。把每个阶段再分成 $s_i$ 个子区间，即 $t_{i-1}={\theta }_{i,0}<{\theta }_{i,1}<\cdots <{\theta }_{i,s_i}=t_i$。底物在一个子区间流加，下一个子区间不流加，即

$v\left(t\right)=\{\begin{array}{ll}0.02,\hfill & t\in \left[{\theta }_{i,2k},{\theta }_{i,2k+1}\right],\hfill \\ 0,\hfill & t\in \left[{\theta }_{i,2k+1},{\theta }_{i,2k+2}\right],\hfill \end{array}k=0,1,\cdots ,\frac{s_i-2}{2},i=1,2,\cdots ,N$ (10)

如此交替进行，且在 $\left[t_{i-1},t_i\right]$ 阶段内，每次流加时长相同，两次流加之间间隔的时长也相同。记 $\left[t_{i-1},t_i\right]$ 阶段内底物每次流加时长为 ${\tau }_i$，即 ${\tau }_i={\theta }_{i,2k+1}-{\theta }_{i,2k},i=1,2,\cdots ,N$，并将一次流加的开始到下一次流加的开

始称为一个流加控制周期，其时长记为 ${\delta }_i$，即 ${\delta }_i={\theta }_{i,2k}-{\theta }_{i,2k-2}$， $k=1,2,\cdots ,\frac{s_i}{2},i=1,2,\cdots ,N$。在生物实验

中，一般取 ${\delta }_i$ 为一个固定常数，即 ${\delta }_i=\delta$。根据上面叙述，有

$0\le {\tau }_i\le \delta ,i=1,2,\cdots ,N$ (11)

令 $\tau =\left({\tau }_1,{\tau }_2,\cdots ,{\tau }_N\right)$，并令 $\Gamma$ 为包含所有满足约束的 $\tau$ 的集合。由 $\tau$ 可知，当 $\tau$ 给定后，则v在任何时刻的值可唯一确定，记为 $v\left(t;\tau \right)$。批式流加发酵过程控制系统描述如下：

$\stackrel{\dot{}}{X}=\left({\mu }_X-d_X\right)X,$ (12)

$\stackrel{\dot{}}{S}=-q_{S}X+\frac{{\rho }_S-S}{V}v\left(t\right),$ (13)

$\stackrel{\dot{}}{V}=v\left(t\right),$ (14)

其中， $d_X$ 是细胞的比衰减率， ${\rho }_S$ 是培养液中底物的浓度， ${\mu }_X$ 是细胞的比生长率，以及 $q_S$ 是底物的比消耗率。具体形式如下：

${\mu }_X={\mu }_m\frac{S}{S+K_S}\left(1-\frac{S}{S^{*}}\right),$ (15)

$q_S=m_S+\frac{{\mu }_X}{Y_S}.$ (16)

这里， ${\mu }_m$ 是细胞的最大比生长率， $K_S$ 是饱和常数， $S^{*}$ 是细胞停止生长的底物浓度的临界值。 $m_S$ 和 $Y_S$ 是动力学参数。

事实上，在不同的发酵阶段 ${\mu }_m$ 和 $m_S$ 会发生变化，因此，我们考虑把 ${\mu }_m$ 和 $m_S$ 看作是不确定参数。假设不确定参数的一阶矩和二阶矩分别是 $\bar{\mu }$ 、 ${\sigma }_1$ 以及 $\bar{m}$ 、 ${\sigma }_2$。为叙述方便，令

$f\left(x,v,{\mu }_m,m_S\right):={\left(\left({\mu }_X-d_X\right)X,-q_{S}X+\frac{{\rho }_S-S}{V}v\left(t\right),v\left(t\right)\right)}^{\top }$。

4.1. 最优控制问题

本算例考虑的最优控制问题如下：以100 s为控制周期，即 $\delta =100\text{s}$ 选取合适的流加时间 $\tau$，使得生物浓度在终端时刻达到最大。该最优控制模型描述如下：

$\begin{array}{l}(OCP)\underset{\tau }{\min }\underset{F}{\max }{\mathbb{E}}_{F}h\left(x\left(t_f;\tau ,v,\left({\mu }_m,m_S\right)\right)\right):=-x_1\left(t_f;\tau ,v,\left({\mu }_m,m_S\right)\right)\\ \text{s}\text{.t}\text{.}\stackrel{\dot{}}{x}\left(t\right)=f\left(x,v,{\mu }_m,m_S\right),t\in \left[0,t_f\right],x\left(0\right)=x^0,\\ \tau \in \Gamma ,\\ {\mu }_m~F\in \mathcal{F}\left(\bar{\mu },{\sigma }_1^2\right)=\left\{F:{\mathbb{E}}_F\left({\mu }_m\right)=\bar{\mu },{\mathbb{E}}_F{\left({\mu }_m-\bar{\mu }\right)}^2={\sigma }_1^2\right\},\\ m_S~F\in \mathcal{F}\left(\bar{m},{\sigma }_2^2\right)=\left\{F:{\mathbb{E}}_F\left(m_S\right)=\bar{m},{\mathbb{E}}_F{\left(m_S-\bar{m}\right)}^2={\sigma }_2^2\right\}.\end{array}$ (17)

令 ${\mu }_m^j$， $m_S^i$ 分别是参数 ${\mu }_m$ 、 $m_S$ 的可能取值， $q_{\mu }^j$ 和 $q_m^i$ 是其相应的概率，即 $\mathbb{P}\left({\mu }_m={\mu }_m^j\right)=q_{\mu }^j$， $\mathbb{P}\left(m_S=m_S^i\right)=q_m^i$， $j=1,2,\cdots ,l$， $i=1,2,\cdots ,n$。设 $q_{\mu }:=\left(q_{\mu }^1,\cdots ,q_{\mu }^l\right)$， $q_m:=\left(q_m^1,\cdots ,q_m^n\right)$。上述最优控制问题(OPC)可以等价于以下最优控制问题(OPC1)：

$\begin{array}{l}\left(\text{OPC}1\right)\underset{\tau }{\min }\underset{q_{\mu },q_m}{\max }{\displaystyle \underset{j=1}{\overset{l}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{q}_{\mu }^j}}{q}_m^{i}h\left(x\left(t_f;\tau ,v,\left({\mu }_m^j,m_S^i\right)\right)\right):=-{\displaystyle \underset{j=1}{\overset{l}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{q}_{\mu }^j}}{q}_m^i{x}_1\left(t_f;\tau ,v,\left({\mu }_m^j,m_S^i\right)\right)\\ \text{s}\text{.t}\text{.}\stackrel{\dot{}}{x}\left(t\right)=f\left(x,v,{\mu }_m,m_S\right),t\in \left[0,t_f\right],x\left(0\right)=x^0,\\ \tau \in \Gamma ,\\ {\displaystyle \underset{j=1}{\overset{l}{\sum }}{q}_{\mu }^j=1,}\end{array}$

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{q}_m^i=1,}\\ {\displaystyle \underset{j=1}{\overset{l}{\sum }}{\mu }_m^j{q}_{\mu }^j=1,}\\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{m}_S^i{q}_m^i=1,}\\ {\displaystyle \underset{j=1}{\overset{l}{\sum }}{\left({\mu }_m^j\right)}^2{q}_{\mu }^j={\bar{\mu }}^2+{\sigma }_1^2,}\end{array}$ (18)

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(m_s^i\right)}^2{q}_m^i={\bar{m}}^2+{\sigma }_2^2,}\\ q_{\mu }^j\ge 0,\\ q_m^i\ge 0.\end{array}$

4.2. 数值结果

设初始值为 $x^0=\left(0.1,20,3\right)$， $\bar{\mu }=3.0$， ${\sigma }_1=0.1$， ${\mu }_m\in \left[0.8\bar{\mu },1.2\bar{\mu }\right]$， $\bar{m}=2.2$， ${\sigma }_2=0.2$， $m_S\in \left[0.8\bar{m},1.2\bar{m}\right]$， $d_X=0.05$， $K_s=280$， $Y_s=0.082$， ${\rho }_S=945$， $t_f=25\text{h}$。将总的发酵时间分成25个阶段，即0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < 11 < 12 < 13 < 14 < 15 < 16 < 17 < 18 < 19 < 20 < 21 < 22 < 23 < 24 < 25。在不确定参数 ${\mu }_m$ 和 $m_S$ 的连续分布的离散化中，我们在区间 $\left[0.8\bar{\mu },1.2\bar{\mu }\right]$ 和区间

$\left[0.8\bar{m},1.2\bar{m}\right]$ 上分别各选择了8个特征元素 ${\left\{{\mu }_m^j\right\}}_{j=1}^8$， ${\left\{m_S^i\right\}}_{i=1}^8$，这里 ${\mu }_m^j=0.8\bar{\mu }+\frac{j-1}{7}0.4\bar{\mu }$，

$m_S^i=0.8\bar{m}+\frac{i-1}{7}0.4\bar{m},j=1,2,\cdots ,8,i=1,2,\cdots ,8$。利用改进的欧拉法对系统进行数值计算，其中步长为

1/3600。在算法(3.1)中， $M=51$， $N_{ite}=150$ 以及 ${\varphi }_1={\varphi }_1=0.1$。算法通过Python软件编程实现，在AMD Ryzen 7 4800H的处理器下求解问题(OCP1)一次的运行时长约为117小时。此时，得到的最优 $q_{\mu }^{*}$ = (1.79×10⁻⁵, 2.46 × 10⁻⁵, 1.37 × 10⁻⁴, 5.22 × 10⁻¹, 4.70 × 10⁻¹, 1.14 × 10⁻⁴, 1.56 × 10⁻⁴, 7.37 × 10⁻³)， $q_m^{*}$ = (1.50 × 10⁻¹, 8.24 × 10⁻⁴, 1.76 × 10⁻², 3.27 × 10⁻², 6.65 × 10⁻¹, 1.03 × 10⁻¹, 2.19 × 10⁻², 8.20 × 10⁻³)，在这个结果下

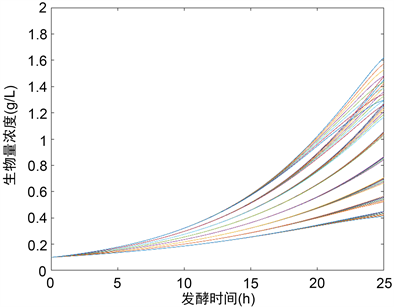
Figure 1. The concentrations of biomass under ${\mu }_m={\mu }_m^j$, $m_S=m_S^i$ and ${\tau }^{*}$

图1. 在 ${\mu }_m={\mu }_m^j$， $m_S=m_S^i$ 和最优 ${\tau }^{*}$ 下，生物量的浓度变化

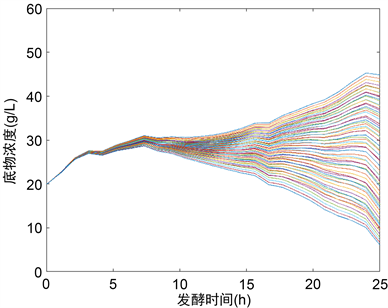
Figure 2. The concentrations of substrate under ${\mu }_m={\mu }_m^j$, $m_S=m_S^i$ and ${\tau }^{*}$

图2. 在 ${\mu }_m={\mu }_m^j$， $m_S=m_S^i$ 和最优 ${\tau }^{*}$ 下，底物的浓度变化

得到的最优切换信号 ${\tau }^{*}$ = (0.000, 49.353, 60.000, 33.102, 5.868, 30.660, 24.768, 27.960, 0.100, 13.893, 7.750, 14.415, 17.429, 22.922, 27.714, 34.639, 15.891, 44.281, 36.272, 39.631, 36.491, 49.297, 60.000, 54.140, 12.930) (s)。在以上最优 $q_{\mu }^{*}$， $q_m^{*}$ 和最优 ${\tau }^{*}$ 下得到的最优值为−0.95465。图1和图2给出了在 ${\mu }_m={\mu }_m^j$， $m_S=m_S^i$ 和最优 ${\tau }^{*}$ 下生物量浓度和底物浓度的轨迹。

5. 结论

本文考虑了多参数不确定切换系统分布鲁棒最优控制问题。以不确定参数已知的一阶矩和二阶矩为约束，以最差期望性能为目标性能，建立切换系统分布鲁棒最优控制模型。利用非线性规划方法对内层问题进行求解，再利用竞争粒子群方法对外层进行求解。最后，以一类微生物批式流加发酵分布鲁棒最优控制问题对切换系统分布鲁棒最优控制问题的应用进行了说明。数值结果显示了算法的有效性。

基金项目

国家自然科学基金面上项目(11671335)；福建省自然科学基金项目(2021J01660)。