1. 引言
地震从孕育到成核直至断层破裂以及震后调整的整个动力学过程,摩擦本构关系始终起着决定性的作用。目前应用最为广泛的4种典型摩擦本构关系,它们分别是:滑移弱化摩擦关系,速率弱化摩擦关系,以及速率–状态相依摩擦关系中的弱化定律和滑动定律。摩擦关系不仅控制着地震的成核位置、发生时间及震级大小,还控制着破裂的方式、破裂的传播速度及方向以及余震发生的数目及其衰减规律。本文主要探究基于速率状态的摩擦关系中的弱化定律和滑动定律,探究其在正应力恒定和变化下摩擦系数的表达式,然后对两种主要的速度–摩擦本构模型进行对比分析,遴选出适合于本研究的模型类别。并对影响摩擦性质的本构关键参数进行讨论,并且针对摩擦定律主要在前人限于实验室的研究条件下采用数值分析方法描述不同参数对变速滑移过程产生影响的定量过程。特别是对速率与摩擦系数的关系有了较为清晰的结果。
2. 经典速率和状态摩擦准则
2.1. 静摩擦下摩擦系数的变化表达式
Dieterich做静摩擦实验时发现,静摩擦系数与摩擦面之间的静摩擦时长的对数呈现明显的线性关系,符合以下表达式 [1]:
(1)
这里f表示摩擦系数;f0,a,b均为常数;t是摩擦面之间的接触时长。在假设b = 1.0的条件下,Dieterich (1972)测得花岗岩、杂砂岩、石英岩和砂岩的系数a的平均值分别为0.022,0.012,0.020,0.016,而这四种岩石的摩擦系数f0则在0.7∼0.8之间 [2]。
2.2. 动摩擦下摩擦系数的变化表达式(正应力恒定时)
与静摩擦相比,动摩擦中摩擦面的接触时间是由滑动速率和接触变化的临界位移量来决定的。因此Dieterich (1979)进一步提出动摩擦系数可能对摩擦滑动的速率具有依赖性,并且他通过设计被称为“三明治型”的直剪岩石摩擦实验证实了这一猜想:摩擦面的接触时间表示为 [2]:
(2)
这里的t表示滑动摩擦过程中的接触时间;Dc是岩石的特征滑动距离,表示更新接触表面需要滑动的距离;
代表滑动摩擦中的滑动速率。
把(2)带入(1)可以得到:
(3)
(3)可以看出摩擦系数的确与滑动速率的对数呈现负相关。但是式(3)只能描述稳态条件下摩擦系数对滑动速率的依赖性,而不能表达速率变化情况下过渡阶段中摩擦系数与滑动速率的关系摩擦系数与接触时间对数的正相关和与滑动速率对数的负相关可以被抽象 [3]:
(4)
但是Ruina (1983, 1980)在总结Dieterich的理论和实验结果以及其他摩擦实验结果时注意到,slide-hold-slide实验中最大摩擦其实与静止之前的滑动历史、有效接触时外力作用的历史以及重新滑动时的滑动速率等因素都有关系。去掉了摩擦系数表达式中显式的时间项,转而引入与时间相关的状态变量
[4] [5]。这样一来,摩擦面的剪切力就可以用滑动速率和一系列的状态变量来表示:
(5)
如果只考虑一个状态变量,而且正应力恒定的情况下,摩擦系数
可描述为速率状态摩擦准则。
(6)
从(6)可以看粗在正应力恒定的条件下,如果滑动速率由v0变到v,摩擦系数会对速率的变化产生一个瞬间的直接响应,再最终稳态,(6)变为
(7)
(6)到(7)的变化体现了先瞬态直接响应为
,稳态过程为
,且当v逐渐增加时,摩擦系数先增加变化量为
,再减小变化量为
[6]。
现在来探究当
的时候,状态变量变化情况:
aging law:
(8)
时,(8)变为
,在弱化本构方程中,愈合是有时间效应的,因此滑动停止时,状态变量依然在变化。
slip law:
(9)
时,(9)变为
,滑动速率
时,状态变量不变,说明滑动处于静止时,状态变量是保持不变的,因此它无法顾及静止接触时间效应 [7]。
但上述的(1) (2)在稳定接触下,
,
。
时,摩擦系数会随着速率的增加而增加,因此称为速率强化过程;当
时,摩擦系数会随着速率的增加而减小,因此称为速率弱化过程。
2.3. 正应力变化下的摩擦系数变化
Linker and Dieterich (1992)和Chester (1994)分别研究了包含正应力和温度影响的摩擦本构方程 [8]。Linker and Dieterich (1992)通过实验表明在正应力变化的情况下,状态变量受到的正应力变化的影响可以表示为:
(10)
(8)或(9)。
是实验得至的无量纲参数。引入了新的摩擦参数c,表示剪切应力变化对状态变量的影响。
(11)
3. 单自由度弹簧滑块模型稳定性分析及数值模拟
3.1. 单自由度弹簧滑块模型稳定性分析
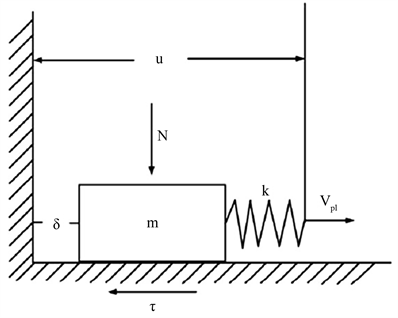
Figure 1. Schematic diagram of a single degree of freedom spring slider model
图1. 单自由度弹簧滑块模型示意图
由图1可知由于加载点在以恒定的速率Vpl运行,所以加载点的位移u会不断加大,弹簧的拉伸则会使得弹性势能不断增加,这时滑块应满足动力学方程:
(12)
其中的摩擦力
应满足速率状态摩擦准则:
(13)
其中
是摩擦系数的表达式,
是slip law或者aging law。
由于滑块的运动速度都非常小,因此由滑块产生的惯性项在通常情况下是可以忽略的 [9],这样就有
(14)
定义
(15)
把(3) (4)结合进行泰勒展开且只保留一阶项:
(16)
(17)
(6)的解可写为:
(18)
把(7)带入(6)得
(19)
以s为变量的一元二次方程的解为:
(20)
由(3)可知
,令
带入(8)有
(21)
从(9)可知,当s > 0时,扰动会随着时间的增长而成指数级增加,系统的稳定性会被破坏。由于
所以D > 0,如果要求s > 0,那么T就必须小于0,从而有
(22)
从上面的分析可以看出,当弹簧滑块系统中的弹簧刚度小于某一刚度时,系统在很小的扰动下就会不稳定,这一刚度是由正应力
,从上面的分析可以看出,当弹簧滑块系统中的弹簧刚度小于某一刚度时,系统在很小的扰动下就会不稳定,这一刚度是由正应力
,(b − a)值和特征滑动距离Dc来确定的,称之为临界刚度 [10]。
(23)
从临界刚度的表达式可以看出,当(a − b) > 0时,即速率强化的情况下,临界刚度始终是负值,而任何弹簧的刚度都不可能小于它,所以此时系统一定是稳定的,而当(a − b) < 0时,即速率弱化的情况下,系统才可能出现不稳定现象。
我们考虑了理想断层中某一点的有效正应力和摩擦阻力的演化(见图2)。作为一个概念练习,我们假设摩擦根据速率状态方程演变,并采用法向应力和切向应力的简单演变,将问题简化为0-D系统:总法向应力保持恒定,因此有效法向应力仅因孔隙压力的变化而变化,切向应力也保持恒定。通过这些简化,系统响应完全由速率–状态方程以及给定的孔隙压力演化来表征。单调增加的压力会引起状态变量和摩擦系数的增加。从图形上看,莫尔包络线在压力积聚阶段逆时针旋转,
,而代表断层处的应力分量点
向左移动(图2,蓝色)。当孔隙压力趋于稳定(
)时,有效应力分量保持不变,而状态变量和摩擦系数松弛回到其稳态值
和
。
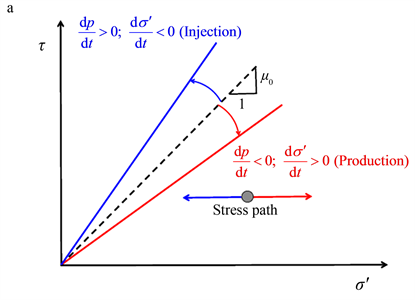
Figure 2. Evolution of effective normal stress and frictional resistance
图2. 有效正应力和摩擦阻力的演化
在这个摩擦放松阶段,包络线顺时针旋转,可能导致在静摩擦系数等于甚至大于初始值
。相反的效果(破坏包络线的明显减弱和顺时针方向),将观察到孔隙压力下降D概念断层模型中本构参数对活化延迟的影响,孔隙压力演化与图2相同。在这些图中,有效法向应力是压缩的。
3.2. Slide-Hold-Slide Experiments
我们使用滑动–保持–滑动实验来说明正则化对摩擦愈合的影响(见图3)。通过这个测试,我们想要阐明V* (更准确地说,特征时间
)对保持期间摩擦演化的影响,以及对滑入后观察到的摩擦系数峰值的影响。我们考虑一个样本,它最初以速度Vs/r在稳态中滑动20 s,再经过100 s的保持期后,滑动恢复到相同的速度Vs/r。我们设定Vs/r = 10 μm/s和模型参数:a = 0.005, b = 0.01, Dc = 10 μm,归一化机械刚度k = 0.001 μm−1。我们还设
= 0.6,V* = 10−6 m/s,使特征时间有意地小,
= 3500 s。
3.3. Velocity Step Experiments
我们采用经典的准静态弹簧块结构,其中样品以速度v1 = 1 μm/s在稳态下滑动10 s,在某一点滑移率瞬间增加到v2 = 1 μm/ s滑动31 s (图4)。为简单起见,我们设模型参数Dc = 10 μm, a = 0.005, b = 0.01,并选择
,使在速率下v1的稳态摩擦在所有案例中都是相同的。以下都用的Dieterich law。
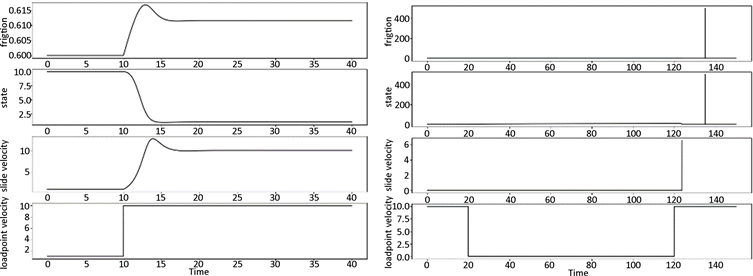
Figure 3. Dieterich law and Ruina law
图3. Dieterich law和Ruina law

Figure 4. One state variable b = 0.01, Dc = 5 μm. Two state variables b = 0.01, Dc = 10 μm and b = 0.001, Dc = 5 microns
图4. 一个状态变量b = 0.01, Dc = 5 μm。两个状态变量b = 0.01, Dc = 10 μm和b = 0.001, Dc = 5 μm
4. 总结
本文通过探究静摩擦下和动摩擦下摩擦系数的表达式,发现静摩擦系数与摩擦面之间的静摩擦时长的对数呈现明显的线性关系。摩擦系数的确与滑动速率的对数呈负相关,(a − b) > 0时,摩擦系数会随着速率的增加而增加,因此称为速率强化过程;当(a − b) < 0时,摩擦系数会随着速率的增加而减小,因此称为速率弱化过程。在0-D模型下,单调增加的压力会引起状态变量和摩擦系数的增加,当弹簧滑块系统中的弹簧刚度小于某一刚度时,系统在很小的扰动下就会不稳定。最后通过“slide-hold-slide”实验和“velocity step experiments”分别探究了Dieterich law和Ruina law摩擦系数的变化。模拟过程中将问题简化为0-D系统:总法向应力保持恒定,因此有效法向应力仅因孔隙压力的变化而变化,切向应力也保持恒定。通过这些简化,系统响应完全由速率–状态方程以及给定的孔隙压力演化来表征。单调增加的压力会引起状态变量和摩擦系数的增加。