度和与边数条件下过线性森林圈的一些研究

Researches on the Cycles through Linear Forest under the Conditions of Degree Sum and Edge Number

摘要: 2009年，Faudree提出在给定的σ₂(G)条件下，图G过(k,t)-线性森林的(k,t,2t+k)-泛圈问题。本文证明了在该σ₂(G)条件下，对任意，G中存在长为r或r+1的圈过(k,t)-线性森林。此外，本文还给出了图G是(k,t)-哈密顿的一个边数条件。

Abstract: In 2009, Faudree proposed the (k,t,2t+k) -pancyclic problem of graph G passing through (k,t) - linear forest under given σ₂(G) condition. In this paper, we prove that under the σ₂(G) condi-tion, for any , there exists a cycle passing through (k,t) -linear forest of length r or r+1 in the graph G. In addition, an edge number condition that graph G is (k,t)-Hamiltonian is given.

1. 引言

本文只考虑无自环和重边的简单图。下面先给出一些基本的定义和符号， $V\left(G\right)$， $E\left(G\right)$ 和 $\delta \left(G\right)$ 分别表示图G的点集、边集和最小度；图G的点数 $\left|V\left(G\right)\right|$ 记为n，边数 $\left|E\left(G\right)\right|$ 记为m， $d_G\left(u\right)$ 表示图G中点u的度数。对于一个非完全图G，定义 ${\sigma }_2\left(G\right)=\min \left\{d_G\left(u_1\right)+d_G\left(u_2\right)\right\}$，其中 $u_1$ 、 $u_2$ 是任意两个不相邻点对。图G中包含了所有点的圈称为哈密顿圈，一个存在哈密顿圈的图称为哈密顿图。一个 $\left(k,t,s\right)$ -线性森林是一个由k条边、t条路构成的线性森林，且t条路中有s条单点路。当一个线性森林F中单点路的数量未知时，简称F为 $\left(k,t\right)$ -线性森林。如果对于G中的任意 $\left(k,t\right)$ -线性森林F，G中都存在一个哈密顿圈包含F，那么称G是 $\left(k,t\right)$ -哈密顿的。给定整数m和n ( $k+t\le m\le n$ )，如果对于任意的 $\left(k,t\right)$ -线性森林及任意的整数 $r\left(m\le r\le n\right)$，G中都存在长度为r的圈包含这个线性森林，那么称G是 $\left(k,t,m\right)$ -泛圈的。本文未定义的术语可参考文献 [1]。

1952年，Dirac [2] 给出：设G是一个阶数 $n\ge 3$ 的图，如果最小度 $\delta \left(G\right)\ge n/2$，那么G是哈密顿的。1960年，Ore [3] 把上述结论推广到不相邻两点度和条件下哈密顿圈存在的结果：设G是一个阶数 $n\ge 3$ 的图，如果 ${\sigma }_2\left(G\right)\ge n$，那么G是哈密顿的。在此基础上，Kronk [4] 研究了过k-路的圈，并分别给出了不相邻两点度和条件和边数条件下的结论：设G是一个n阶图且满足 ${\sigma }_2\left(G\right)\ge n+k$ 或满足边数 $m\ge \left(n-1\right)\left(n-2\right)/2+k+2$，那么G是k-路哈密顿的。Faudree [5] 等人把过k-路的圈推广到过 $\left(k,t\right)$ -线性森林的情况。

定理1 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2\le k+t\le n$，F是一个 $\left(k,t\right)$ -线性森林。如果

(i) ${\sigma }_2\left(G\right)\ge n+k$，当 $F=P_{k+1}\cup \left(t-1\right)K_1$ 时，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$，其他情况，

那么G是 $\left(k,t\right)$ -哈密顿的，其中 $2|\left(n-k\right)$ 时 $\epsilon \left(n,k\right)=1$，否则 $\epsilon \left(n,k\right)=0$。此外， ${\sigma }_2\left(G\right)$ 的条件是紧的。

除了研究哈密顿圈外， [5] 还研究了泛圈性的结果，并提出一个改进度和条件下的问题。

定理2 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2\le k+t\le n$，F是一个 $\left(k,t\right)$ -线性森林。如果 ${\sigma }_2\left(G\right)\ge n+k$，那么G是 $\left(k,t,2t+k\right)$ -泛圈的。

问题 [5] 令G是一个n阶图，k，t和n是正整数且满足 $2\le k+t\le n$，F是一个 $\left(k,t\right)$ -线性森林。如果

(i) ${\sigma }_2\left(G\right)\ge n+k$，当 $P_{k+1}\subseteq F$ 时，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$，其他情况，

那么G是 $\left(k,t,2t+k\right)$ -泛圈的吗？

何剑在 [6] 中尝试解决上述问题，给出了在 $\left(k,t,0\right)$ -线性森林的情况下一个结果。本文基于Faudree等人提出的上述问题猜想，将 [6] 中的结论推广到 $\left(k,t\right)$ -线性森林的情况，即线性森林中可以有单点路。此外，本文还给出了图G是 $\left(k,t\right)$ -哈密顿的一个边数条件。

2. 主要结果

本文证明了以下结果：

定理3 设k，t和n是正整数，满足 $2\le k+t\le n$，G是n阶图，F是 $\left(k,t\right)$ -线性森林，如果

(i) ${\sigma }_2\left(G\right)\ge n+k$，当 $F=P_{k+1}\cup \left(t-1\right)K_1$，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$，其他情况，

则对任意 $r\in \left[\max \left\{4,k+2t\right\},n\right]$，G中存在长为r或 $r+1$ 的圈过F。

定理4 设k，t和n是正整数，满足 $2\le k+t\le n$，G是n阶图，F是 $\left(k,t\right)$ -线性森林，如果边数

(i) $m\ge \left(n-1\right)\left(n-2\right)/2+k+2$，当 $F=P_{k+1}\cup \left(t-1\right)K_1$ 时，

(ii) $m\ge \left(n-1\right)\left(n-2\right)/2+k+2-\epsilon \left(n,k\right)$，其他情况，

那么G是 $\left(k,t\right)$ -哈密顿的，其中 $2|\left(n-k\right)$ 时 $\epsilon \left(n,k\right)=1$，否则 $\epsilon \left(n,k\right)=0$。

3. 证明

首先给出证明过程中需要用到的两个引理。

引理6 [6] 设 $k=t=1$，G是阶 $n\ge k+t$的图，F是G中 $\left(k,t,t-k\right)$ -线性森林。如果 ${\sigma }_2\left(G\right)\ge n+k$，则G中存在过F的长度不大于4的圈。

引理7 [6] 设G是阶 $n\ge k+t$的图，其中k，t为满足 $k\le t$ 的正整数。设F是G中 $\left(k,t,t-k\right)$ -线性森林。如果

(i) ${\sigma }_2\left(G\right)\ge n+k$， $k=1$ 时，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$， $k\ge 2$ 时，

则当 $t\ge 2$ 时，G存在过F的圈C，使得 $C-V\left(F\right)$ 为孤立点图或空图。

在证明定理3前还需要给出两个定理来辅助证明。

定理8 设G是阶 $n\ge k+t$的图，其中k，t为满足 $k\le t$ 的正整数。设F是G中 $\left(k,t,t-k\right)$ -线性森林。如果G中存在长度为 $r\le n-1$ 的过F的圈，并且

(i) ${\sigma }_2\left(G\right)\ge n+k$， $k=1$ 时，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$， $k\ge 2$ 时，

则G中存在长为 $r+1$ 或 $r+2$ 的圈过F。

证明 假设图G中不存在过F的长度为 $r+1$ 或 $r+2$ 的圈。已知G中存在长为 $r\le n-1$ 的过F的圈，记为 $C_0=v_1{v}_2\cdots v_r{v}_1$，那么有 $H_0=G-C_0\ne \varnothing$。因为 ${\sigma }_2\left(G\right)\ge n+k-1$，所以G是 $k+1$ -连通图，不妨设 $v_{1}z$ 是连接 $C_0$ 和 $H_0$ 的边，且有 $v_1{v}_2\notin E\left(F\right)$。那么 $v_{2}z\notin E\left(G\right)$，且 $N\left(v_2\right)\cap N\left(z\right)\subseteq V\left(C_0\right)$，否则G中就存在过F的长度为 $r+1$ 或 $r+2$ 的圈。故而 $P_0=v_2{v}_3\cdots v_r{v}_{1}z$是G中过F的且长度为r的路。

设 $P=u_1{u}_2\cdots u_{r+1}$ 是G中一条长为r的路，且满足

(I) $E\left(F\right)\subseteq E\left(P\right)$， $V\left(F\right)\subseteq V\left(P\right)$， $u_{r+1}\notin V\left(F\right)$，

(II) 在(I)的前提下， $\left|\left\{u_1{u}_2\right\}\cap E\left(F\right)\right|$ 最大。

由前边的分析知， $P_0=v_2{v}_3\cdots v_r{v}_{1}z$ 是G中满足条件(I)的路，因此假设中选择的路P是存在的。

如果 $u_1{u}_{r+1}\in E\left(G\right)$，那么G中存在长为 $r+1$ 的圈 $u_1{u}_2\cdots u_{r+1}{u}_1$ 过F；如果 $u_1$， $u_{r+1}$ 在 $H=G-V\left(P\right)$ 中有公共邻点z，那么G中存在长为 $r+2$ 的圈 $u_1{u}_2\cdots u_{r+1}z{u}_1$ 过F。故而假设 $u_1{u}_{r+1}\notin E\left(G\right)$ 且 $N_H\left(u_1\right)\cap N_H\left(u_{r+1}\right)=\varnothing$。因此， $d_H\left(u_1\right)+d_H\left(u_{r+1}\right)\le \left|H\right|=n-r-1$。

令 $X=\left\{j|1\le j\le r,u_1{u}_{j+1}\in E\left(G\right)\right\}$， $Y=\left\{j|1\le j\le r,u_j{u}_{r+1}\in E\left(G\right)\right\}$，则 $X\cap Y\subseteq \left\{j|u_j{u}_{j+1}\in E\left(F\right)\right\}$，否则 $\exists j\in X\cap Y$ 使得 $u_1{u}_{j+1},u_j{u}_{r+1}\in E\left(G\right)$， $u_j{u}_{j+1}\notin E\left(F\right)$，那么圈 $u_1{u}_2\cdots u_j{u}_{r+1}{u}_r\cdots u_{j+1}{u}_1$ 过F且长度为 $r+1$ (如图1)。

Figure 1. Schematic diagram of cycle $u_1{u}_2\cdots u_j{u}_{r+1}{u}_r\cdots u_{j+1}{u}_1$

图1. 存在圈 $u_1{u}_2\cdots u_j{u}_{r+1}{u}_r\cdots u_{j+1}{u}_1$ 的示意图

于是， $d_P\left(u_1\right)+d_P\left(u_{r+1}\right)=\left|X\right|+\left|Y\right|=\left|X\cup Y\right|+\left|X\cap Y\right|\le \left|\left[1,r\right]\right|+\left|E\left(F\right)\right|=r+k$，故得 $d_G\left(u_1\right)+d_G\left(u_{r+1}\right)=d_H\left(u_1\right)+d_P\left(u_1\right)+d_H\left(u_{r+1}\right)+d_P\left(u_{r+1}\right)\le n+k-1$。

(i) $k=1$ 时， ${\sigma }_2\left(G\right)\ge n+k$，矛盾。

(ii) $k\ge 2$ 时， ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$，故而 $\epsilon \left(n,k\right)=1$，从而有 $d_G\left(u_1\right)+d_G\left(u_{r+1}\right)=n+k-1$，同时 $\left|X\cup Y\right|=\left|\left[1,r\right]\right|$， $\left|X\cap Y\right|=\left|E\left(F\right)\right|$。

如果 $u_1{u}_2\in E\left(F\right)$，则 $1\in X\cap Y$，那么 $u_1{u}_{r+1}\in E\left(G\right)$，与先前的假设矛盾。也就是说对于任何满足(I)的路 $P=u_1{u}_2\cdots u_{r+1}$ 都有 $u_1{u}_2\notin E\left(F\right)$。类似地，也有 $u_r{u}_{r+1}\notin E\left(F\right)$。

设 $u_i{u}_{i+1}$ 和 $u_j{u}_{j+1}$ 是P上两条不被其他F-边间隔的F-边， $u_s$ 是 $P\left(u_{i+1},u_j\right]$ 的第一个F中的孤立点且 $u_{j+2}\notin V\left(F\right)$。由 $\left|X\cap Y\right|=\left|E\left(F\right)\right|$ 有， $i,j\in X\cap Y$，从而有 $u_{i+1},u_{j+1}\in N\left(u_1\right)$， $u_i,u_j\in N\left(u_{r+1}\right)$。

下面先考虑s的取值，首先有 $s\ne j$。若 $s=j$，那么存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_s{u}_{r+1}{u}_r\cdots u_{j+2}$ 与P的选取矛盾(如图2)。

Figure 2. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_s{u}_{r+1}{u}_r\cdots u_{j+2}$

图2. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_s{u}_{r+1}{u}_r\cdots u_{j+2}$ 的示意图

如果 $s\ne i+2$，则 $s\ge i+3$，那么 $P\left(u_{i+1},u_s\right)$ 内存在点 $u_{i+2}$。由 $\left|X\cup Y\right|=\left|\left[1,r\right]\right|$ 可知， $u_{i+2}\in N\left(u_1\right)$ 或 $u_{i+2}\in N\left(u_{r+1}\right)$，但上述两条件不同时成立，否则与之前的假设矛盾。当 $u_{i+2}\in N\left(u_1\right)$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{i+2}{u}_{i+3}\cdots u_{r+1}$ 与P的选取矛盾(如图3)。

Figure 3. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{i+2}{u}_{i+3}\cdots u_{r+1}$

图3. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{i+2}{u}_{i+3}\cdots u_{r+1}$ 的示意图

当 $u_{i+2}\in N\left(u_{r+1}\right)$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{i+2}{u}_{r+1}{u}_r\cdots u_{j+2}$ 与P的选取矛盾(如图4)。因此 $s=i+2$。

Figure 4. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{i+2}{u}_{r+1}{u}_r\cdots u_{j+2}$

图4. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{i+2}{u}_{r+1}{u}_r\cdots u_{j+2}$ 的示意图

如果 $u_1{u}_s\in E\left(G\right)$，则路 $u_{i+1}{u}_i\cdots u_1{u}_s{u}_{i+3}\cdots u_{r+1}$ 与P的选取矛盾(如图3)。因此， $u_1{u}_s\notin E\left(G\right)$。如果 $u_s{u}_{r+1}\in E\left(G\right)$，则路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{r+1}{u}_r\cdots u_{j+2}$ 与P的选取矛盾(如图5)。因此， $u_s{u}_{r+1}\notin E\left(G\right)$。

Figure 5. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{r+1}{u}_r\cdots u_{j+2}$

图5. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_s{u}_{r+1}{u}_r\cdots u_{j+2}$ 的示意图

此外，有 $N_H\left(u_1\right)\cap N_H\left(u_s\right)=\varnothing$，否则 $\exists z\in N_H\left(u_1\right)\cap N_H\left(u_s\right)$，又因为 $u_{r+1}\notin V\left(F\right)$，故而存在路 $u_{i+1}{u}_i\cdots u_{1}z{u}_s{u}_{s+1}\cdots u_r$ 与P的选取矛盾(如图6)。

Figure 6. Schematic diagram of path $u_{i+1}{u}_i\cdots u_{1}z{u}_s{u}_{s+1}\cdots u_r$

图6. 存在路 $u_{i+1}{u}_i\cdots u_{1}z{u}_s{u}_{s+1}\cdots u_r$ 的示意图

也有 $N_H\left(u_s\right)\cap N_H\left(u_{r+1}\right)=\varnothing$，否则 $\exists y\in N_H\left(u_s\right)\cap N_H\left(u_{r+1}\right)$，当 $r=j+1$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y$ 与P的选取矛盾(如图7)；当 $r\ge j+2$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y{u}_{r+1}{u}_r\cdots u_{j+3}$ 与P的选取矛盾(如图8)。

Figure 7. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y$

图7. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y$ 的示意图

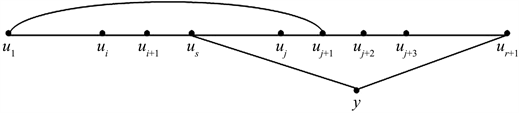
Figure 8. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y{u}_{r+1}{u}_r\cdots u_{j+3}$

图8. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{s}y{u}_{r+1}{u}_r\cdots u_{j+3}$ 的示意图

故而有， $d_H\left(u_1\right)+d_H\left(u_s\right)\le n-r-1$， $d_H\left(u_s\right)+d_H\left(u_{r+1}\right)\le n-r-1$。

令 $P_1=u_1{u}_2\cdots u_{i+1}$， $P_2=u_{i+2}{u}_{i+3}\cdots u_{r+1}$。

令 $X_1=\left\{l|1\le l\le i,u_1{u}_{l+1}\in E\left(G\right)\right\}$， $Y_1=\left\{l|2\le l\le i+1,u_l{u}_s\in E\left(G\right)\right\}$，则 $X_1\cap Y_1\subseteq \left\{l|2\le l\le i,u_l{u}_{l+1}\in E\left(F\right)\right\}=I_1$，否则 $\exists l\in X_1\cap Y_1$ 使得 $u_1{u}_{l+1},u_l{u}_s\in E\left(G\right)$， $u_l{u}_{l+1}\notin E\left(F\right)$，那么路 $u_{i+1}{u}_i\cdots u_{l+1}{u}_1{u}_2\cdots u_l{u}_s{u}_{i+3}\cdots u_{r+1}$ 与P的选取矛盾(如图9)。

Figure 9. Schematic diagram of path $u_{i+1}{u}_i\cdots u_{l+1}{u}_1{u}_2\cdots u_l{u}_s{u}_{i+3}\cdots u_{r+1}$

图9. 存在路 $u_{i+1}{u}_i\cdots u_{l+1}{u}_1{u}_2\cdots u_l{u}_s{u}_{i+3}\cdots u_{r+1}$ 的示意图

从而有， $d_{P_1}\left(u_1\right)+d_{P_1}\left(u_s\right)\le \left|X_1\cup Y_1\right|+\left|X_1\cap Y_1\right|\le \left|V\left(P_1\right)\right|+\left|I_1\right|$。

令 $X_2=\left\{l|i+2\le l\le r-1,u_1{u}_l\in E\left(G\right)\right\}$， $Y_2=\left\{l|i+2\le l\le r,u_s{u}_{l+1}\in E\left(G\right)\right\}$，则 $X_2\cap Y_2\subseteq \left\{l|i+2\le l\le r-1,u_l{u}_{l+1}\in E\left(F\right)\right\}=I_2$，否则 $\exists l\in X_2\cap Y_2$ 使得 $u_1{u}_l,u_s{u}_{l+1}\in E\left(G\right)$， $u_l{u}_{l+1}\notin E\left(F\right)$，那么路 $u_{i+1}{u}_i\cdots u_1{u}_l{u}_{l-1}\cdots u_s{u}_{l+1}{u}_{l+2}{u}_{r+1}$ 与P的选取矛盾(如图10)。

Figure 10. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_l{u}_{l-1}\cdots u_s{u}_{l+1}{u}_{l+2}{u}_{r+1}$

图10. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_l{u}_{l-1}\cdots u_s{u}_{l+1}{u}_{l+2}{u}_{r+1}$ 的示意图

从而有， $d_{P_2}\left(u_1\right)+d_{P_2}\left(u_s\right)\le \left|X_2\cup Y_2\right|+\left|X_2\cap Y_2\right|\le \left|V\left(P_2\right)\right|-1+\left|I_2\right|$。

因此， $d_P\left(u_1\right)+d_P\left(u_s\right)\le \left|V\left(P\right)\right|-1+\left|E\left(F\right)\right|=r+k$。

令 $X_3=\left\{l|1\le l\le i,u_s{u}_{l+1}\in E\left(G\right)\right\}$， $Y_3=\left\{l|2\le l\le i+1,u_l{u}_{r+1}\in E\left(G\right)\right\}$，则 $X_3\cap Y_3\subseteq \left\{l|2\le l\le i,u_l{u}_{l+1}\in E\left(F\right)\right\}=I_3$，否则 $\exists l\in X_3\cap Y_3$ 使得 $u_{l+1}{u}_s,u_l{u}_{r+1}\in E\left(G\right)$， $u_l{u}_{l+1}\notin E\left(F\right)$，那么路 $u_{i+1}{u}_i\cdots u_{l+1}{u}_s{u}_{i+3}\cdots u_{r+1}{u}_l{u}_{l-1}\cdots u_1$ 与P的选取矛盾(如图11)。

Figure 11. Schematic diagram of path $u_{i+1}{u}_i\cdots u_{l+1}{u}_s{u}_{i+3}\cdots u_{r+1}{u}_l{u}_{l-1}\cdots u_1$

图11. 存在路 $u_{i+1}{u}_i\cdots u_{l+1}{u}_s{u}_{i+3}\cdots u_{r+1}{u}_l{u}_{l-1}\cdots u_1$ 的示意图

从而有， $d_{P_1}\left(u_s\right)+d_{P_1}\left(u_{r+1}\right)\le \left|X_3\cup Y_3\right|+\left|X_3\cap Y_3\right|\le \left|V\left(P_1\right)\right|+\left|I_3\right|$。

令 $X_4=\left\{l|i+2\le l\le r-1,u_s{u}_{l+1}\in E\left(G\right)\right\}$， $Y_4=\left\{l|i+3\le l\le r,u_l{u}_{r+1}\in E\left(G\right)\right\}$，则 $X_4\cap Y_4\subseteq \left\{l|i+3\le l\le r-1,u_l{u}_{l+1}\in E\left(F\right)\right\}=I_4$，否则 $\exists l\in X_4\cap Y_4$ 使得 $u_{l+1}{u}_s,u_l{u}_{r+1}\in E\left(G\right)$， $u_l{u}_{l+1}\notin E\left(F\right)$，那么当 $j+1<l$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_{j+2}\cdots u_l{u}_{r+1}{u}_r\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_j$ 与P的选取矛盾(如图12)。当 $j+1>l+1$ 时，路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_l{u}_{r+1}{u}_r\cdots u_{j+2}$ 与P的选取矛盾(如图13)。

Figure 12. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_{j+2}\cdots u_l{u}_{r+1}{u}_r\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_j$

图12. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_{j+2}\cdots u_l{u}_{r+1}{u}_r\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_j$ 的示意图

Figure 13. Schematic diagram of path $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_l{u}_{r+1}{u}_r\cdots u_{j+2}$

图13. 存在路 $u_{i+1}{u}_i\cdots u_1{u}_{j+1}{u}_j\cdots u_{l+1}{u}_s{u}_{s+1}\cdots u_l{u}_{r+1}{u}_r\cdots u_{j+2}$ 的示意图

从而有， $d_{P_2}\left(u_s\right)+d_{P_2}\left(u_{r+1}\right)\le \left|X_4\cup Y_4\right|+\left|X_4\cap Y_4\right|\le \left|V\left(P_2\right)\right|-1+\left|I_4\right|$。

因为 $u_1{u}_2,u_r{u}_{r+1}\notin E\left(F\right)$，又 $u_s$ 是F上的孤立点，即 $u_{i+1}{u}_s,u_s{u}_{i+3}\notin E\left(F\right)$，故而 $I_3+I_4=E\left(F\right)$。因此， $d_P\left(u_s\right)+d_P\left(u_{r+1}\right)\le \left|V\left(P\right)\right|-1+\left|E\left(F\right)\right|=r+k$。

故而有， $d_G\left(u_1\right)+d_G\left(u_s\right)\le n+k-1$， $d_G\left(u_s\right)+d_G\left(u_{r+1}\right)\le n+k-1$，又因为 $u_1{u}_s\notin E\left(G\right)$， $u_s{u}_{r+1}\notin E\left(G\right)$，有 $d_G\left(u_1\right)+d_G\left(u_s\right)\ge n+k-1$， $d_G\left(u_s\right)+d_G\left(u_{r+1}\right)\ge n+k-1$，所以 $d_G\left(u_1\right)+d_G\left(u_s\right)=n+k-1$， $d_G\left(u_s\right)+d_G\left(u_{r+1}\right)=n+k-1$。

那么 $2\left(d_G\left(u_1\right)+d_G\left(u_s\right)+d_G\left(u_{r+1}\right)\right)=3\left(n+k-1\right)$。由 $\epsilon \left(n,k\right)=1$ 知，n，k奇偶性相同，而上式等号两边奇偶性不同，矛盾。所以假设不成立，定理8成立。

定理9 设G是阶 $n\ge k+t$的图，其中k，t为满足 $k\le t$ 的正整数。设F是G中 $\left(k,t,t-k\right)$ -线性森林。如果

(i) ${\sigma }_2\left(G\right)\ge n+k$， $k=1$ 时，

(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$， $k\ge 2$ 时，

则对任意 $r\in \left[\max \left\{4,k+2t\right\},n\right]$，G中存在长为r或 $r+1$ 的圈过F。

证明 由引理6和引理7可知，G中存在长度不超过 $\max \left\{4,k+2t\right\}$ 的圈过F，记为 $C_{r_0}$。要证明定理9，只需证明在 $r\ge r_0$ 时，G中存在长度为r或 $r+1$ 的圈过F。

用归纳法，当 $r=r_0$ 时，G中有长为r的圈过F，显然成立。

假设结论对给定的r成立，下面证对 $r+1$ 也成立，即证G中有长度为 $r+1$ 或 $r+2$ 的圈过F。因为对于给定的r，有长为r或 $r+1$ 的圈过F。如果存在长为 $r+1$ 的圈过F，那么得证，如果不存在长为 $r+1$ 的圈过F，那么存在长为r的圈过F，再由定理8可知，一定存在长为 $r+2$ 的圈过F。故定理得证。

定理3的证明 当 $F\ne P_{k+1}\cup \left(t-1\right)K_1$ 时，设G是含F的n阶图， ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$。在G中去掉F路中的所有内部点，即对于每条长度大于1的路，都用一条边将其代替，得到图 $G^{\prime }$。设总共去掉了 $k-k^{\prime }$ 个内部点，使得原线性森林F变成了 $\left(k^{\prime },t\right)$ -线性森林 $F^{\prime }$，且新得到的线性森林每条路的长都为0或1，也即 $\left(k^{\prime },t,t-k^{\prime }\right)$ -线性森林。那么 $G^{\prime }$ 的阶数变为 $n^{\prime }=n-\left(k-k^{\prime }\right)=n-k+k^{\prime }$。对于 $G^{\prime }$ 中的任意两个不相邻点，其度和至多减少 $2\left(k-k^{\prime }\right)$，又有 $\epsilon \left(n^{\prime },k^{\prime }\right)=\epsilon \left(n,k\right)$，所以 ${\sigma }_2\left(G^{\prime }\right)\ge n+k-\epsilon \left(n,k\right)-2\left(k-k^{\prime }\right)=n^{\prime }+k^{\prime }-\epsilon \left(n^{\prime },k^{\prime }\right)$。由定理9知，对任意 $r^{\prime }\ge \max \left\{4,k^{\prime }+2t\right\}$ 且 $r^{\prime }\le n^{\prime }$，G中有长为 $r^{\prime }$ 或 $r^{\prime }+1$ 的圈过 $F^{\prime }$。通过将 $G^{\prime }$ 中 $F^{\prime }$ 的每条边换成G中对应的路，就可由 $G^{\prime }$ 中过 $F^{\prime }$ 的圈得到相应的G中过F的圈，圈的长度对应变化，故而，对任意 $r\in \left[\max \left\{4,k+2t\right\},n\right]$，G中存在长为r或 $r+1$ 的圈过F。

当 $F=P_{k+1}\cup \left(t-1\right)K_1$ 时， ${\sigma }_2\left(G\right)\ge n+k$，通过类似的方法去内部点再还原，可得结论仍成立。故得证。

定理4的证明 先证情况(i)， $F=P_{k+1}\cup \left(t-1\right)K_1$ 时。如果G是完全图，那么对于任意的 $\left(k,t\right)$ -线性森林，G中一定有一个哈密顿圈过这个线性森林。故而假设G不是完全图。设u、v是G中一对不相邻点， $V\left(H\right)=V\left(G\right)-\left\{u,v\right\}$，H是由 $V\left(H\right)$ 导出的G的子图。由前边定义有 $E\left(G\right)=d_G\left(u\right)+d_G\left(v\right)+E\left(H\right)$。又因为 $E\left(H\right)\le \left(n-2\right)\left(n-3\right)/2$，所以可以得到 $d_G\left(u\right)+d_G\left(v\right)=E\left(G\right)-E\left(H\right)\ge \left(n-1\right)\left(n-2\right)/2+k+2-\left(n-2\right)\left(n-3\right)/2=n+k$，因此由定理1可得，G是 $\left(k,t\right)$ -哈密顿的。

情况(ii)类似，同样通过定理1可证，故定理得证。

下面给出一个例子说明定理2情况(i)的界是紧的。令 $K_{n-1}$ 是一个完全图，点集 $V\left(K_{n-1}\right)=\left\{v_1,v_2,\cdots ,v_{n-1}\right\}$ 外另有一点v，且v与 $K_{n-1}$ 上的 $k+1$ 个点 $v_1,v_2,\cdots ,v_{k+1}$ 相邻，由这n个点构成的图即为图 $G_1$。可知 $E\left(G_1\right)=\left(n-1\right)\left(n-2\right)/2+k+1$。取线性森林 $F_1=P_{k+1}\cup \left(t-1\right)K_1$，其中 $P_{k+1}=v_1{v}_2\cdots v_{k+1}$，同时在 $K_{n-1}$ 中另取 $t-1$ 个其余点。显然， $G_1$ 中没有一个哈密顿圈能包含这个线性森林 $F_1$。

4. 结语

本文研究了在(i) ${\sigma }_2\left(G\right)\ge n+k$，当 $F=P_{k+1}\cup \left(t-1\right)K_1$，(ii) ${\sigma }_2\left(G\right)\ge n+k-\epsilon \left(n,k\right)$，其他情况，这两种条件下，对任意 $r\in \left[\max \left\{4,k+2t\right\},n\right]$，G中存在长为r或 $r+1$ 的圈过 $\left(k,t\right)$ -线性森林的问题，是对Faudree提出的过 $\left(k,t\right)$ -线性森林的 $\left(k,t,2t+k\right)$ -泛圈问题新的探索，目前猜想并未被完全证明，仍是比较困难的问题。另一方面，本文从边数的角度给出了图G是 $\left(k,t\right)$ -哈密顿的一个条件。

NOTES

^*通讯作者。