1. 引言
页岩气藏天然裂缝发育,水平井多簇压裂裂缝呈现网状形态 [1] [2],有必要开展复杂缝网扩展数值模拟研究,以阐述复杂缝网扩展规律。关于裂缝扩展数值模拟研究方面,国内外有大量的学者提出了不同的求解方法,主要包括:有限元方法 [3]、扩展有限元方法 [4]、边界元法 [5]、离散元法 [6]、相场法 [7] 和近场动力学方法 [8] 等。结合有限元方法和内聚区模型广泛应用于求解裂缝扩展问题,同样适用于页岩气藏压裂复杂缝网扩展问题。为此,本文建立了页岩气藏复杂缝网扩展流固耦合模型,并采用有限元方法和内聚区模型求解应力场和裂缝扩展过程,对水平井多簇裂缝扩展开展了数值模拟研究,分析了水平应力差和射孔簇数对复杂缝网形态的影响。
2. 裂缝扩展数学模型
2.1. 岩体变形
假设水力压裂过程中岩体变形为准静态,需满足平衡方程为:
(1)
式中:σ为总应力,Pa;f为体积力,Pa/m。
根据Biot固结理论,有效应力的表达式为:
(2)
式中:σ'为有效应力,Pa;pm为基质孔隙压力,Pa;α为Biot固结系数,无量纲。
采用线弹性力学本构关系描述岩体变形:
(3)
式中:D为弹性刚度矩阵。
2.2. 流体流动
考虑水力压裂过程中压裂液在裂缝内流动、基质中流动以及两者之间的滤失窜流。基质中流体流动连续性方程为:
(4)
式中:M为Biot模量,Pa;t表示时间,s;εv表示体积应变,无量纲;qt和qb表示单位时间裂缝上下表面流入到基质的滤失量,m3/s;Vm表示基质单元体积,m3;δmt和δmb表示裂缝单元与基质单元连接信息,当裂缝单元与基质单元相邻时取值为1,否则为0。
裂缝内流体流动连续性方程为:
(5)
式中:w为裂缝宽度,m;pf为裂缝内流体压力,Pa;μ表示流体黏度,Pa∙s;Sf表示裂缝单元面积,m2;Qf表示裂缝内源汇项,m/s。
流体在裂缝与基质之间的窜流量计算公式为:
(6)
(7)
式中:c为滤失系数,m3/(Pa∙s);pt和pb表示与裂缝上下表面相邻的基质单元内流体压力,Pa。
2.3. 裂缝扩展准则
目前已有文献提出了较多的裂缝扩展准则,本文采用内聚区模型来描述水力裂缝延伸和天然裂缝激活过程。内聚区模型主要包括损伤起始准则和损伤演化规律。
采用最大名义应力准则描述损伤起始准则:
(8)
式中:tn为垂直于裂缝面牵引力,Pa,且
;ts和tt为裂缝面上互相垂直的牵引力,Pa;
为临界垂向牵引力,且
,
为临界切向牵引力,Pa。
损伤演化规律由牵引力–张开位移关系决定,通常采用双线性模型来描述,随着张开位移增大,牵引力线性增加,在张开位移的临界点达到临界牵引力,此时微裂缝开始产生;之后牵引力随着张开位移的增大而减小直到消失,张开位移达到最大值,界面完全分离。损伤因子的演化公式为:
(9)
式中:δf为最大张开位移,m;δ0为临界张开位移,m;δmax为单元经历的最大的张开位移,m。
3. 数值求解方法
水力裂缝扩展问题涉及应力场和压力场耦合迭代求解,分别采用有限元方法和有限体积方法对应力场和压力场进行离散,其中岩体变形有限元弱形式为:
(10)
式中:u为虚位移;tc为内聚力。
对流体连续性方程进行时间和空间积分,得到压力场积分形式为:
(11)
4. 计算结果分析
4.1. 模型验证
为验证所构建的裂缝扩展数学模型及算法的准确性,计算模拟100 m × 50 m矩形区域内KGD模型 [9] 水力裂缝扩展结果,并与近似解析解进行对比。KGD模型假设裂缝等高,缝内压力与缝宽之间的关系满足:
(12)
式中:w为裂缝宽度,m;L为裂缝半长,m;G为剪切模量,Pa;v为泊松比;σmin为最小主应力,Pa;f1、f2和fL和表示当前位置与裂缝半长的比值(x/L)。
此外,裂缝内流体压力方程满足:
(13)
式中:pw为井筒处压力,Pa;h为裂缝高度,m;q0为注入速率,m3/(m∙s)。
Geertsma和De Klerk推导得到模型的近似解析解,其中裂缝半长L、井筒处缝宽w0随时间t的演化关系为:
(14)
(15)
式中:E'为平面应变杨氏模量,Pa;q0为注入速率,m3/(m∙s)。
模型的基本参数包括:杨氏模量E = 25 GPa,泊松比v = 0.2,注入速率q0 = 0.01 m3/(m∙s),流体粘度μ = 10 mPa∙s。计算对比结果如图1和图2所示,由图可知,本文数值模型能准确求解水力裂缝扩展问题。

Figure 1. Comparison of fracture half-length between numerical and analytical solutions
图1. 裂缝半长数值解与解析解对比
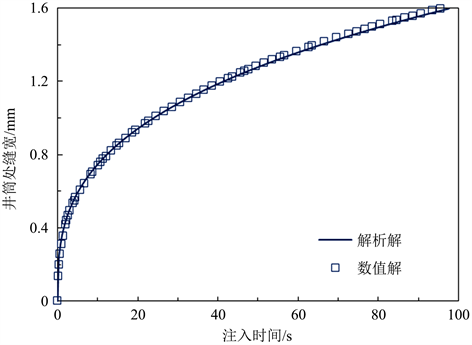
Figure 2. Comparison of fracture width at the inlet of wellbore between numerical and analytical solutions
图2. 井筒处裂缝宽度数值解与解析解对比
4.2. 水平应力差的影响
多簇裂缝同步扩展存在应力阴影作用,计算模拟了不同水平应力差条件下复杂缝网扩展过程。以四簇压裂为例,簇间距为10 m时裂缝扩展结果如图3所示。由图可知,水平应力差越大,压裂裂缝越容易穿过天然裂缝,形成的裂缝形态越集中,分散性越差。
根据裂缝扩展结果,计算相应的裂缝改造面积结果如图4所示,其中不同颜色代表采用不同的簇间距。由图可知,不论选取何种簇间距,随着水平应力差增大,裂缝改造面积减小;当水平应力差大于7 MPa时,选择簇间距为15 m可取得最大的裂缝改造面积。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 3. Results of hydraulic fracture propagation under different conditions of stress difference: (a) Δσ = 5 MPa; (b) Δσ = 7 MPa; (c) Δσ = 9 MPa
图3. 不同应力差条件下水力裂缝扩展结果:(a) Δσ = 5 MPa;(b) Δσ = 7 MPa;(c) Δσ = 9 MPa

Figure 4. Results of fracture stimulated area under different conditions of stress difference
图4. 不同应力差条件下裂缝改造面积结果
4.3. 射孔簇数的影响
射孔簇数越多,多簇裂缝同步扩展时应力阴影作用越强,计算模拟了不同射孔簇数条件下水力裂缝扩展结果。取水平应力差为7 MPa,簇间距为15 m,求解得到三簇、四簇和五簇裂缝同步扩展结果如图5所示。由图可知,射孔簇数越多,沟通的天然裂缝越多,形成的裂缝形态越分散。
同理,计算获得不同射孔簇数条件下裂缝改造面积结果如图6所示,其中不同颜色代表采用不同的簇间距。由图可知,当簇间距小于20 m时,随着射孔簇数增大,裂缝改造面积先增大后减小;而当簇间距为20 m时,随着射孔簇数增大,裂缝改造面积逐渐增大。
 (a)
(a) 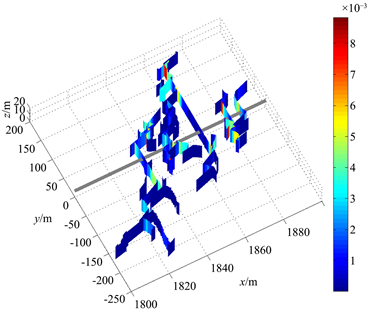 (b)
(b)  (c)
(c)
Figure 5. Results of hydraulic fracture propagation under different conditions of cluster number: (a) Three clusters; (b) Four clusters; (c) Five clusters
图5. 不同簇数条件下水力裂缝扩展结果:(a) 三簇;(b) 四簇;(c) 五簇

Figure 6. Results of fracture stimulated area under different conditions of cluster number
图6. 不同簇数件下裂缝改造面积结果
5. 结论
本文在考虑流固耦合效应的基础上,建立了页岩气藏水力压裂裂缝扩展数学模型,采用有限元方法和有限体积方法对应力场和压力场进行了离散求解,通过与解析解对比,验证了模型的准确性,进而分析了页岩气藏水平井多簇压裂时水平应力差和射孔簇数对复杂缝网形态的影响,获得的结论主要包括:
1) 多簇压裂裂缝扩展存在应力阴影作用,水平应力差越小,则应力阴影作用越强,裂缝扩展形态越集中,裂缝改造面积越小;当水平应力差大于7 MPa时,选择簇间距为15 m可获得最大的裂缝改造面积;
2) 多簇射孔压裂,射孔簇数越多,应力阴影作用越强,沟通的天然裂缝越多,形成的裂缝形态越分散;当簇间距小于20 m时,随着射孔簇数增大,裂缝改造面积先增大后减小。
NOTES
*通讯作者。