基于双层模糊逻辑方法的智能车辆行驶稳定性研究

Driving Stability of Intelligent Vehicles Based on Double-Layer Fuzzy Logic Method

摘要: 为提高智能车辆紧急工况下的自主维稳能力，提出一种基于双层模糊逻辑方法的行车稳定性自动调节策略。首先分析了车辆行驶稳定性影响参数，制定相应参数的理想约束范围，搭建车辆二自由度参考模型。其次将模型参数理想值与实际值偏差作为模糊逻辑输入量，然后引入额外比例因子和量化因子，实现内外双层自适应调节。最后将模糊逻辑输出的期望横摆力矩转换为纵向力矩，再基于摩擦椭圆理论分配给各轮，实现分布式前馈控制。在五次多项式路径下进行对比仿真试验，结果表明，所提出的双层模糊自适应调节策略可将车辆行驶稳定性提高20%以上。

Abstract: In order to improve the intelligent vehicles’ stability maintenance capability under emergency conditions, an automatic adjustment strategy of driving stability based on a two-layer fuzzy logic method is proposed. Firstly, the vehicle driving stability influencing parameters are analyzed, the ideal constraint range of corresponding parameters is formulated, and the vehicle two-degree-of-freedom reference model is built. Secondly, the deviation between the ideal and actual values of the model parameters is taken as the input quantity of the fuzzy logic, and then additional scaling factors and quantization factors are introduced to realize the internal and external two-layer adaptive adjustment. Finally, the desired yaw moment output from the fuzzy logic is converted into longitudinal moment, and then distribute to each wheel based on the friction ellipse theory to realize distributed feed forward control. Comparative simulation tests are conducted under five polynomial paths, and the results show that the proposed two-layer fuzzy adaptive regulation strategy can improve the vehicle driving stability by more than 20%.

1. 引言

智能汽车技术的快速发展进一步解放了人类双手，但同时人们也对智能汽车的行驶安全提出了更高的要求 [1] 。车辆行驶稳定性作为行车安全的首要问题，引起了国内外学者的广泛研究。为降低智能车辆在行驶过程中的安全隐患，首先应明确车辆稳定性评估指标有哪些，再对这些影响参数进行控制调节，即可有效提高行车安全性能 [2] 。如下为现阶段的常见稳定性调控方法的成果概述，以及本文研究方向的背景及研究原因的阐述。

现有成果中常见的稳定性调控方法有：模型预测控制法(MPC) [3] ，北京大学机械与汽车电子工程学院郭宁远等人将该方法与分布式驱动相结合 [4] ，保证了给定的安全约束并降低了计算量，并验证出此方法同样适用于AEV [5] 。同时北京交通大学田英等人利用此方法实现驱动切换，将主动前轮转向与外部横摆力矩相协调，有效提高自动驾驶车辆防侧偏侧翻稳定性 [6] 。滑模控制方法(SMC) [7] ：西南交通大学王凯等人设计了全局快速终端滑模跟踪控制器，使得车辆具有更好的动态边界协同控制能力 [8] 。韩国釜山国立大学Anugrah提出在现有导航方法基础上利用滑模面调整的避障策略，得到更好的驱动控制能力及转向性能，以此提高避障稳定性 [9] 。除此之外，英国考文垂大学Taghavifar等人提出一种基于阻尼最小二乘反向传播神经网络杂交的最优鲁棒控制法 [10] ；同时还有Javier等人通过监测驾驶员意图及车辆行驶状况及参数，再配合转矩分配及牵引系统调控行车稳定性 [11] 。瑞典林雪平大学Fors Victor等人更是提出一种新的概念：可达力概念——将轮胎与路面相互作用产生的力进行矢量化，优化车辆总力及力矩调配，以实现鲁棒性最优控制调节 [12] 。

模糊逻辑控制方法最初于20世纪60年代由Lotfi Zadeh提出 [13] ，其最大优势在于不需个人对问题有具体的数学描述，而是将其纳入一种专家数据库中进行控制解决。文献中已有许多关于模糊逻辑控制在电动汽车中的应用研究 [14] [15] [16] 。据上述成果表明，极限工况下的前馈型稳定性研究尚不充足，本文利用模糊逻辑控制的优势，打破特定行驶环境的反馈型研究局限，提出一种智能车辆稳定性自主前馈型调节策略。通过分析稳定性影响参数，建立车辆动力学模型，基于模糊逻辑结构简单、易进行人机交互等优点，叠加额外的比例因子和量化因子，设计适用性更好的内外双层控制策略，并结合横摆力矩分配原则，最终实现自适应分布式前馈控制调节。

2. 车辆稳定性参数分析及模型搭建

2.1. 稳定性影响参数分析

根据车辆轮胎特性，当车辆以较高车速行驶，轮胎处于非线性区域即紧急条件下，此时应主要考虑车辆航向角变化情况 [17] ，根据航向角组成定义，判断各参数对车辆稳定性的影响。车辆横摆角 $\gamma$ 值越大，转向半径越小，转向越灵敏；反之则转向越迟钝。如图1所示：当地面附着系数 $\mu$ 及 ${\delta }_f$ 一定，车辆低速行驶时， $\stackrel{\dot{}}{\gamma }$ 与车速v成正比，但随着车辆加速，达到路面附着极限， $\stackrel{\dot{}}{\gamma }$ 与车速v则成反比。质心侧偏角 $\beta$ ，较大时， $\stackrel{\dot{}}{\gamma }$ 、 $\beta$ 对车辆位姿及行驶轨迹有影响，需同时对二者进行控制，进而维持车辆行驶稳定性。车辆航向角 $\phi$ 为质心速度与X轴夹角，当 $\beta$ 较小时， $\phi$ 近似等于 $\gamma$ ，由此得出三者之间关系： $\phi =\gamma +\beta$ 。

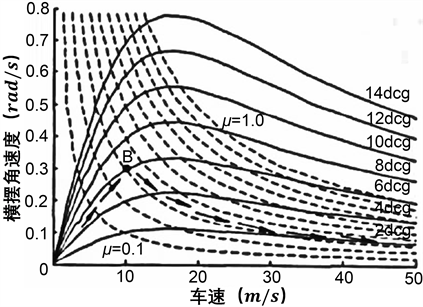
Figure 1. Graph of vehicle yaw velocity vs. vehicle speed

图1. 车辆横摆角速度与车速关系曲线图

2.2. 基于影响参数的车辆参考模型建立

车辆转向主要考虑自身横摆运动和侧向运动，得到线性二自由度参考模型：

$\{\begin{array}{l}\left(C_{af}+C_{ar}\right)\beta +\frac{1}{v_x}\left(a{C}_{af}-b{C}_{ar}\right)\gamma -C_{af}{\delta }_f=m\left({\stackrel{\dot{}}{v}}_y+v_x\gamma \right)\\ \left(a{C}_{af}-b{C}_{ar}\right)\beta +\frac{1}{v_x}\left(a^2{C}_{af}+b^2{C}_{ar}\right)\gamma -a{C}_{af}{\delta }_f=I_z\stackrel{\dot{}}{\gamma }\end{array}$ (1)

将其整理为二阶空间状态方程，稳态下理想的质心侧偏角、横摆角速度表达式如下：

$\{\begin{array}{l}{\beta }_d=\frac{ma{v}_x^2{C}_{af}+bL{C}_{af}{C}_{ar}}{C_{af}{C}_{ar}{L}^2+m\left(a{C}_{af}-b{C}_{ar}\right)v_x^2}{\delta }_f\\ {\gamma }_d=\frac{v_{x}L{C}_{af}{C}_{ar}}{L{C}_{af}{C}_{ar}+v_x^{2}m\left(a{C}_{af}-b{C}_{ar}\right)}{\delta }_f\end{array}$ (2)

为保证不同路面附着系数条件下的车辆稳定性，制定期望 $\gamma$ 、 $\beta$ 约束范围， $\gamma$ 在低附着系数路面行驶时， ${\gamma }_{\max }<\gamma$ ；反之 ${\gamma }_{\max }>\gamma$ 。为防止车辆侧滑，侧向加速度 $\stackrel{\dot{}}{y}$ 不得超过路面最大附着系数 $\mu$ ： $\stackrel{\dot{}}{y}\le \mu g$ ；

结合车辆匀速圆周运动侧向加速度公式： $\stackrel{\dot{}}{y}=\frac{v_x}{R}=\gamma v_x$ ，得到横摆角约束范围如下：

$\{\begin{array}{l}{\gamma }_{\max }=\frac{\mu g}{v_x}\\ {\gamma }_d=\min \left\{\left|\gamma \right|,\left|{\gamma }_{\max }\right|\right\}\end{array}$ (3)

车辆进入稳态时， $\stackrel{\dot{}}{\gamma }$ 、 $\stackrel{\dot{}}{\beta }$ 均为零，同时考虑最大路面附着系数条件限制，带入式子(1)得：

$\beta =\left(\frac{b}{L\left[1+\frac{m}{L^2}\left(\frac{a}{C_{af}-C_{ar}}\right)v_x^2\right]}+\frac{ma{v}_x^2}{C_{af}{L}^2\left[1+\frac{m}{L^2}\left(\frac{a}{C_{af}-C_{ar}}\right)v_x^2\right]}\right){\delta }_f=\left(\frac{b}{v_x^2}+\frac{ma}{C_{ar}L}\right)\gamma v_x$ (4)

联立(3)和(4)得到：

${\beta }_{\max }=\left(\frac{b}{v_x^2}+\frac{ma}{C_{ar}L}\right){\gamma }_{\max }{v}_x^2=\mu g\left(\frac{b}{v_x^2}+\frac{ma}{C_{ar}L}\right)$ (5)

与横摆角速度同理得到理想质心侧偏角 $\beta$ 的约束范围：

${\beta }_d=\min \left\{\left|\beta \right|,\left|{\beta }_{\max }\right|\right\}$ (6)

3. 双层模糊逻辑稳定性调节策略

为提高不同行驶工况下车辆稳定性自主调节能力，需提前对可能出现的偏差采取消除措施。本节中在基础模糊逻辑中，引入的额外量化因子和比例因子，对稳定性影响参数的权重系数进行动态调节，计算出期望横摆力矩反馈给车辆，实现闭环前馈调节，有效提升车辆稳定性调控能力。

3.1. 外层权重系数模糊控制器

外层权重系数调节思想：根据车辆实际稳定性影响参数所占比重调节，基于模糊方法计算得到自适应调节期望横摆力矩 $M_z$ ，具体设计流程见图2。

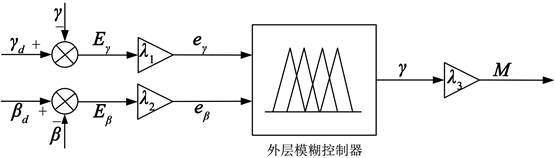
Figure 2. Fuzzy logic of the outer layer yaw moment

图2. 外层横摆力矩模糊逻辑框图

模糊逻辑输入为 $E={\left[E_{\stackrel{\dot{}}{\gamma }}{E}_{\beta }\right]}^{\text{T}}$ ，设定量化因子 ${\lambda }_1$ 、 ${\lambda }_2$ 及比例因子 ${\lambda }_3$ ，对输入量进行模糊化处理，并列出模糊逻辑输出量与期望横摆力矩 $M_z$ 关系式如下：

$\{\begin{array}{l}T\left[e_{\gamma }\right]=\left\{A_{\gamma }^1,A_{\gamma }^2,\cdots ,A_{\gamma }^n\right\}\\ T\left[e_{\beta }\right]=\left\{A_{\beta }^1,A_{\beta }^2,\cdots ,A_{\beta }^n\right\}\end{array}$ (7)

$\{\begin{array}{l}e={\left[{\lambda }_1{E}_{\gamma }{\lambda }_2{E}_{\beta }\right]}^{\text{T}}={\left[e_{\gamma }{e}_{\beta }\right]}^{\text{T}}\\ M_z={\lambda }_3\cdot y\end{array}$ (8)

${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 由两输入量最大偏差 $E_{1_{\max }}$ 、 $E_{2_{\max }}$ 决定， $u_{\max }$ 为输出控制量精确值，n、m、l分别为两输入量及单输出量模糊集论域档数。

${\lambda }_1=\frac{n}{\left|E_{1\max }\right|},{\lambda }_2=\frac{m}{\left|E_{2\max }\right|},{\lambda }_3=\frac{\left|u_{\max }\right|}{l}$ (9)

式子(7)中 $A_{\gamma }^i$ 、 $A_{\beta }^i$ 分别为 $e_{\gamma }$ 、 $e_{\beta }$ 的第i个模糊变量值，是定义在论域 $E_{\gamma }$ 、 $E_{\beta }$ 上的模糊集合，对应的隶属度函数为：

$\{\begin{array}{l}{\mu }_{A_{\gamma }^i}\left[e_{\gamma }\right]=\left(i=1,2,\cdots ,n\right)\\ {\mu }_{A_{\beta }^i}\left[e_{\beta }\right]=\left(i=1,2,\cdots ,n\right)\end{array}$ (10)

输出模糊语言变量的模糊关系定义， $T\left[q\right]=\left\{B^1,B^2,\cdots ,B^m\right\},B^i\left(i=1,2,\cdots ,n\right)$ 是q的第i个模糊变量值，相应的隶属度函数为 ${\mu }_{B^i}\left[y\right]$ ，用于描述输入输出关系的对应模糊规则为： $R_i$ : if $e_{\gamma }=A_{\gamma }^i$ and $e_{\beta }=A_{\beta }^i$ then $y=B^i,i=\left(1,2,\cdots ,n\right)$ ，输入量采用此模糊化方法，可求得对应每条模糊规则的适用度： ${\alpha }_i={\mu }_{A_{\gamma }^i}\left[e_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[e_{\beta }\right]$ ，根据模糊推理得到每条规则对应的输出量总模糊集合及相应隶属度函数：

$\{\begin{array}{l}{\mu }_{B_i}\left[y\right]={\alpha }_i{\mu }_{B_i}\left[y\right]\\ B=U_{i=1}^n{B}_i\to {\mu }_B\left[y\right]=V_{i=1}^n{\mu }_{B_i}\left[y\right]\end{array}$ (11)

模糊量无法直接驱动控制装置，应将输出模糊量转化为精确量，采用加权平均值法进行解模糊化处理得到精确输出如下：

$y=\frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\mu }_{B_i}\left[y_{c_i}\right]}}{{\displaystyle {\sum }_{i=0}^n{\mu }_{B_i}\left[y_{c_i}\right]}}$ (12)

$y_{c_i}$ 是 ${\mu }_{B_i}\left[y\right]$ 的隶属度函数中心点： ${\mu }_{B_i}\left[y_{c_i}\right]=\max \left\{{\mu }_{B_i}\left[y\right]\right\}={\alpha }_i$ ，并带入式子(11) (12)中：

$y=\frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\alpha }_i}}{{\displaystyle {\sum }_{i=0}^n{\alpha }_i}}=\frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\mu }_{A_{\gamma }^i}\left[e_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[e_{\beta }\right]}}{{\displaystyle {\sum }_{i=0}^n{\mu }_{A_{\gamma }^i}\left[e_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[e_{\beta }\right]}}=\frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\mu }_{A_{\gamma }^i}\left[{\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2{E}_{\beta }\right]}}{{\displaystyle {\sum }_{i=0}^n{\mu }_{A_{\gamma }^i}\left[{\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2{E}_{\beta }\right]}}$ (13)

如图2所示外层控制器所示，将模糊逻辑双输入分为7个模糊集，分别为负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)；输出为外层模糊逻辑额外量化因子 $\Delta {\lambda }_1$ 、 $\Delta {\lambda }_2$ 和额外比例因子 $\Delta {\lambda }_3$ ，分为四个模糊子集CH、CL、AL、AH。如图3为相应的隶属度函数和模糊曲面：

(a) (b) (c) (d)

Figure 3. Membership function and outer layer fuzzy logic 3D curves

图3. 隶属度函数及内层模糊逻辑三维曲面图

外层模糊规则如表1所示：

Table 1. Quantization factor and scale factor fuzzy rules

表1. 量化因子及比例因子模糊规则设定

根据控制器参数及解模糊化得到模糊逻辑输入、输出间的函数关系如下，带入式子(13)得到期望横摆力矩 $M_z$ 表达式：

$\{\begin{array}{l}y=f_1\left(e_{\gamma },e_{\beta }\right)=f_1\left({\lambda }_1{E}_{\gamma },{\lambda }_2{E}_{\beta }\right)\\ M_z={\lambda }_3\cdot \frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\mu }_{A_{\gamma }^i}\left[{\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2{E}_{\beta }\right]}}{{\displaystyle {\sum }_{i=0}^n{\mu }_{A_{\gamma }^i}\left[{\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2{E}_{\beta }\right]}}\end{array}$ (14)

增大 ${\lambda }_1$ 、 ${\lambda }_2$ 时可缩小偏差变量基本论域，此时偏差对调节效果有更加显著的影响；反之，调节策略对输入偏差的变化不敏感，调节精度因此降低，产生模糊控制死区，外层模糊控制器失效。调节器响应速度及稳态精度受 ${\lambda }_3$ 影响，当 ${\lambda }_3$ 增大时，控制系统响应加快；当 ${\lambda }_3$ 较小时，系统响应迟钝，控制器稳态精度较差。

3.2. 内层自适应模糊控制器

外层模糊控制器失效时，增加额外量化因子 $\Delta {\lambda }_1$ 、 $\Delta {\lambda }_2$ 及比例因子 $\Delta {\lambda }_3$ ，间接调节 $\beta$ 及 $\stackrel{\dot{}}{\gamma }$ 的权重系数，实现不同行驶工况下的 $M_z$ 动态调节。车辆稳态行驶时，增大 $\Delta {\lambda }_1$ 、 $\Delta {\lambda }_2$ 、 $\Delta {\lambda }_3$ 可提高控制系统响应速度；但当车辆处于非稳态条件时， $\gamma$ 、 $\beta$ 与 ${\gamma }_d$ 、 ${\beta }_d$ 之间存在明显偏差，不仅通过增大 $\Delta {\lambda }_1$ 、 $\Delta {\lambda }_2$ 提高偏差消除速度，同时减小 $\Delta {\lambda }_3$ 来平衡车辆横摆力矩分配，以使车辆稳定行驶。内层自适应模糊逻辑模块与外层权重系数调节模块综合设计框图如图4所示：

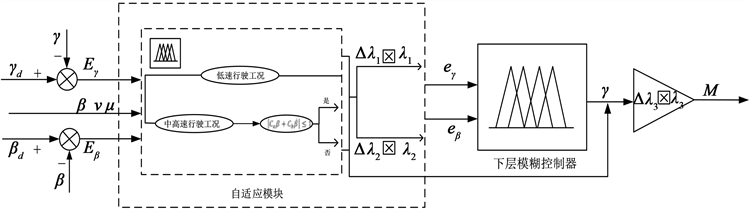
Figure 4. Adaptive regulation fuzzy logic block diagram

图4. 自适应调节模糊逻辑框图

构建综合自适应模糊逻辑输入量，并带入公式(13)中得到期望横摆力矩 $M_z$ ：

$\{\begin{array}{l}{e}_{\gamma }=\left({\lambda }_1\cdot \Delta {\lambda }_1\right)\cdot E_{\gamma }\\ e_{\beta }=\left({\lambda }_2\cdot \Delta {\lambda }_2\right)\cdot E_{\beta }\\ M_z=\left({\lambda }_3\cdot \Delta {\lambda }_3\right)\cdot y=\left({\lambda }_3\cdot \Delta {\lambda }_3\right)\cdot f_2\left(e_{\gamma },e_{\beta }\right)\end{array}$ (15)

车辆低速转弯时，控制 $\stackrel{\dot{}}{\gamma }$ 达到车辆稳定行驶要求，此时输出量应满足 $\Delta {\lambda }_1>1$ 、 $\Delta {\lambda }_2=0$ 、 $\Delta {\lambda }_3>1$ ；但当车辆处于极限工况行驶时， $\beta$ 及其变化率会被限制在条件 $\left|C_a\beta +C_b\stackrel{\dot{}}{\beta }\right|\le 1$ 下，此时自适应模块输出调节因子应满足关系 $\Delta {\lambda }_1=\Delta {\lambda }_2>1$ ，同时为减小车辆两侧扭矩差保持行驶稳定性，输出的 $\Delta {\lambda }_3$ 应小于1；当 $\beta$ 及其变化率不满足约束条件时( $C_a=4.386,C_b=2.562$ [18] )，车辆处于较危险情况， $\beta$ 作为主要被控对象调节车辆稳定性， $\stackrel{\dot{}}{\gamma }$ 对车辆稳定性控制不再起作用，故此时输出调节因子应满足条件 $\Delta {\lambda }_1=0$ 、 $\Delta {\lambda }_2>1$ 、 $\Delta {\lambda }_3>1$ 。

如图4所示自适应模糊逻辑框图，将 $E\left(\gamma \right)$ 和 $E\left(\beta \right)$ 两偏差化为7个模糊集合：负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)；输出 $M_z$ 分为9个模糊集：负极大(NVB)、负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)、正极大(PVB)，共形成49条模糊规则。如图5为输入输出相应隶属度函数及其对应模糊逻辑曲面。

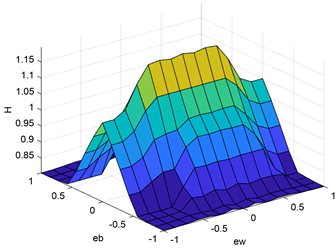(a) (b) (c) (d)

Figure 5. Membership function and inner layer fuzzy logic 3D curves

图5. 隶属度函数及内层模糊逻辑三维曲面图

本文的内层模糊控制规则推理关系如表2所示：

Table 2. Inner fuzzy control rules

表2. 内层模糊控制规则表

与外层模糊控制选择同样的解模糊化方法，得到最终自适应调节的期望横摆力矩 $M_z$ 计算公式如下：

$M_z=\left({\lambda }_3\cdot \Delta {\lambda }_3\right)\cdot \frac{{\displaystyle {\sum }_{i=0}^n{y}_{c_i}{\mu }_{A_{\gamma }^i}}\left[{\lambda }_1\Delta {\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2\Delta {\lambda }_2{E}_{\beta }\right]}{{\displaystyle {\sum }_{i=0}^n{\mu }_{A_{\gamma }^i}}\left[{\lambda }_1\Delta {\lambda }_1{E}_{\gamma }\right]\cdot {\mu }_{A_{\beta }^i}\left[{\lambda }_2\Delta {\lambda }_2{E}_{\beta }\right]}$ (16)

4. 横摆力矩分配策略

基于摩擦椭圆理论对车辆垂向载荷进行优化分配 [19] ，先确保车辆前后轴纵向力与前后轴动态载荷比

值相等： $\frac{F_{xf}}{F_{zf}}=\frac{F_{xr}}{F_{zr}}$ ，再协调扭矩与驱动力矩间控制，将车轮受力及横摆力矩构建转化关系： $F_{xi}=\frac{T_{xi}}{R_w}$ ，

四个车轮总驱动力矩满足以下条件：

$\{\begin{array}{l}{T}_{total}=T_{lf}+T_{lr}+T_{rf}+T_{rr}\\ T_{lr}-T_{lf}+T_{rf}-T_{rr}=\frac{\Delta M_z{R}_w}{t}\end{array}$ (17)

垂向载荷优化分配横摆力矩更易实现且可靠，联立上述方程组，并结合自适应期望横摆力矩公式，获得车辆各轮所分配的纵向力矩，其中Q表示二分之一轮距，q为车辆前后轴所受动态载荷， $R_w$ 为车辆驱动轮滚动半径：

$\{\begin{array}{l}{T}_{lf}=\left(T_{total}-\frac{M_z{R}_w}{Q}\right)\cdot \frac{bg-qh}{2gl}\\ T_{rf}=\left(T_{total}+\frac{M_z{R}_w}{Q}\right)\cdot \frac{bg-qh}{2gl}\\ T_{lr}=\left(T_{total}-\frac{M_z{R}_w}{Q}\right)\cdot \frac{ag+qh}{2gl}\\ T_{rr}=\left(T_{total}+\frac{M_z{R}_w}{Q}\right)\cdot \frac{ag-qh}{2gl}\end{array}$ (18)

5. 仿真试验及分析

5.1. 试验环境及模型参数

为验证所提出稳定性调节方法的可行性，利用CarSim数据接口向Matlab/Simulink中搭建的逻辑框架实时传输车辆信息，调节器计算 $M_z$ 反馈到车辆系统中，形成闭环系统联合仿真。仿真条件设置：仿真道路为五次多项式轨迹，行驶车速v分别取90 km/h和120 km/h，路面附着系数 $\mu$ 取0.8~1，对比有无稳定性调节器的车辆行驶情况，具体评价指标分析如表3所示。

Table 3. Overall vehicle parameters

表3. 整车参数

5.2. 稳定性参数指标分析

行驶中稳定性影响参数 $\beta$ 与 $\stackrel{\dot{}}{\gamma }$ 的值即可有效反应车辆行驶情况，如图6(a)，图6(b)、图6(c)，图6(d)分别为不同速度下的 $\stackrel{\dot{}}{\gamma }$ 、 $\beta$ 曲线对比图。图6(a)，图6(c)中红色曲线为带有稳定性调节器的 $\beta$ 曲线，随着车速提升， $\beta$ 越难调控，带有稳定性调节器的车辆，最大的质心侧偏角在0.2左右；反之，在车速达到120 km/h时，质心侧偏角接近0.4，显然，随车速的不断提高，稳定性调节效果越明显。图6(b)，图6(d)中红色曲线为带有稳定性调节器的 $\stackrel{\dot{}}{\gamma }$ 曲线，带有稳定性调节器的曲线明显更加平滑，抖振幅度减小，两评价指标峰值均降低20%以上，大大降低车辆侧翻风险。

5.3. 期望横摆力矩及分配曲线

横摆力矩及其分配曲线可充分反应车辆行驶稳定性调节过程概况。如图7(a)，图7(c)为左右侧车轮横摆力矩曲线图，随车速增大，所需转向调节力矩也明显增大，红灰色曲线波动幅度更小，有效说明所设计调节逻辑的前馈补偿能力，在实际行驶中，车辆降低所需力矩调节即可维持稳定行驶，曲线尾端是回正后的轻微抖振，波动程度完全在可忽略不计，也因此保证了系统的抗扰动能力。图7(b)，图7(d)验证了左右侧各轮纵向力矩的合理分配，保证内外侧车轮的行驶平衡，这一特点可显著提高行驶舒适性及安全特性。

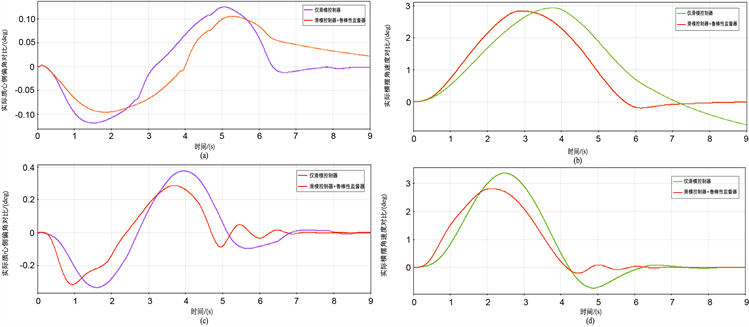
Figure 6. Stability parameter index curves

图6. 稳定性参数指标曲线

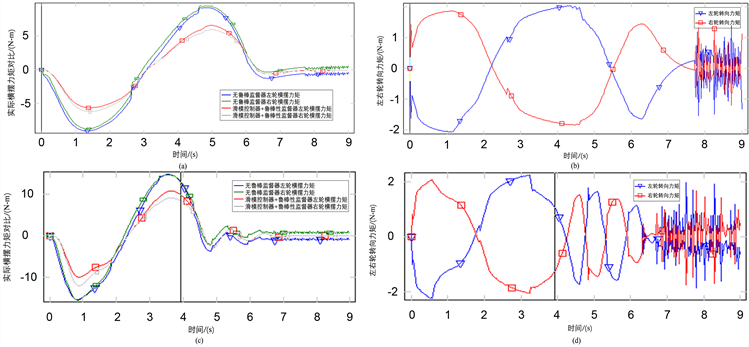
Figure 7. Yaw moment and distribution curves

图7. 横摆力矩及分配曲线

6. 总结

本文以智能车辆横向稳定性为控制目标，车辆横摆角速度和质心侧偏角为被控参数，引入额外比例因子和量化因子，实现各参数权重系数的动态调节，基于双层模糊逻辑方法计算车辆所需的补偿横摆力矩，再根据稳定性需求将期望横摆力矩转化为纵向驱动力矩，并将其分配至左右两侧驱动轮。经仿真试验验证，所提出的双层模糊自适应调节策略可将车辆行驶稳定性提高20%以上，同时发现该种调节策略有较好的容错能力，易于人机界面联系，具有结构简单、各驱动轮转矩独立可控的天然优势，形成车辆稳定性闭环前馈调节。