1. 引言
建筑能源的消耗远超工业和交通部门,住宅和商业建筑的不断增长给城市可持续发展带来了新的挑战,为建筑寻求合适的可再生能源已成为近年来学者的关注热点 [1] 。芬兰工程师Savonius S J [2] 发明的Savonius阻力型垂直轴风力机由于结构简单、建造成本低、不受来流风向控制、良好的自启动能力及建筑复杂风环境适应性而被人们广泛关注 [3] ,但其缺点是功率系数相对较低 [4] 。
为提高阻力型垂直轴风力机的效率,学者们对Savonius风力机结构参数开展了大量的研究工作。几何参数方面,李岩等 [5] 研究发现叶片重叠比0.175时风力机性能最优。Prabowoputra D M等 [6] 对不同相移角叶片的Savonius风力机进行了研究。王军等 [7] 数值模拟研究叶片数量发现了一种能提高转矩和功率的新型Savonius风力机。陈建等 [8] 实验研究发现单层叶轮的风力机能产生更大的转矩。谢晶等 [9] 采用数值模拟研究发现长导风帘导流装置能提高阻力型风力机的运行效率。朱建勇等 [10] 对180˚螺旋式Savonius风力机的气动特性进行了研究。赵振宙等 [11] 研究表明螺旋角为180˚、隔板数为6、螺距为6的螺旋形Savonius叶轮具有较高的风能利用率。Abdelaziz K R等 [12] 对改变叶片弧角的Savonius转子进行了研究。
叶片型线方面,韩立虎等 [13] 数值模拟研究了半圆形叶片风力机。Bach G [14] 提出了Bach叶型。Roy S等 [15] 研究发现的新型椭圆叶型的性能最高能提高34.8%。Aldos [16] 提出了摆动叶型能有效解决叶片回流的问题。Reupke等 [17] 研究发现板条型叶型能明显增强静力矩。田文龙等人 [18] 研究不同扁度对传统Savonius风力机叶轮的影响,结果发现扁度为0.72时叶轮的最大功率高出传统Savonius叶轮5.84%。陈榴等 [1] 发现相较于传统半圆型Savonius风力机,采用流线型翼型或扁平翼型的风力机性能更好。
上述Savonius风力机叶轮研究发现,叶片型线不但会引起叶轮效率的剧烈变化,同时还会改变风轮最佳几何参数组合,为此叶片型线是Savonius风力机优化设计的核心问题之一,也是提升Savonius风力机风能利用率的关键。鉴于前述文献指出扁度小、流线型叶型在风能利用率提升方面极具潜力,本文创新的提出了采用NACA四位数翼型上表面曲线作为Savonius风力机的新叶型,使其具有一定流线型和高升力特性,同时叶型的参数化有利于深入开展关键设计参数对性能影响的研究。
2. Savonius风力机参数
本文研究对象为两叶片Savonius风力机,其结构示意图如图1所示。其主要参数包括:来流风速V,叶轮直径D,端板直径D0,重叠比S,转轴直径a,叶片转动方位角θ。
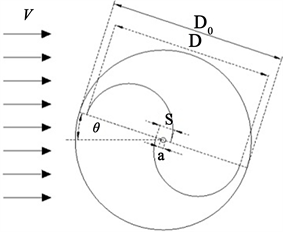
Figure 1. 2D schematic of the Savonius wind turbine
图1. Savonius风力机的二维示意图
3. 计算模型
3.1. 物理模型
本文采用NACA四位数翼型的上表面作为Saovnius风力机的叶片型线。NACA四位数翼型方程主要由最大弯度和最大弯度的位置控制,因此通过改变上述两个设计变量来研究NACA上表面曲线对Savonius风轮性能的影响。NACA翼型的控制方程如下:
其中,c表示翼型弦长;x表示0~c间的点坐标;yc表示翼型厚度的一半;m表示最大弯度;p表示最大弯度的位置。本文基于NACA四位数翼型型线,通过MATLAB构造了12种新型Savonius风力机叶型,如图2所示。

Figure 2. The blade profiles of the wind turbine
图2. 风力机叶型
表1中最左侧第二列叶型由下向上标记为3040 (30为最大弯度,40为最大弯度的位置)、4040、5040和6040。图2各个叶型均与表1中各列一一对应。风力机的其它几何参数固定,叶轮直径D = 210 mm,端盖直径为D0 = 231 mm,叶轮高H = 231 mm,中间转轴直径a为6 mm,重叠比为0.167。

Table 1. Parameters and names of designed blade profiles
表1. 叶型参数和名称
3.2. 计算域和边界条件
由于本文研究的Saovnius风力机叶片轮廓沿延伸方向特征相同,因此将风力机模型简化为二维模型再进行非定常数值模拟,这样既能保证计算结果的可靠性,还能大大降低计算量和计算成本 [19] 。为得到准确的模拟结果,本文选取的计算区域长24D和宽12D,叶轮中心距入口边界的长度为6D,如图3所示。采用滑移网格技术,将计算域分为旋转和静止两个区域,采用Gambit软件进行网格划分,以三角形非结构网格为主,在叶片附近采用四边形边界层网格,并在叶片周围进行局部加密。数值模拟采用Fluent软件进行,所选湍流模型为k-ω SST,入口边界设为速度入口,出口设为压力出口,叶片设为无滑移壁面,上下边界为光滑壁面,入口风速设为8 m/s。

Figure 3. Computational domains and boundary conditions
图3. 计算区域和边界条件
3.3. 数值方法验证
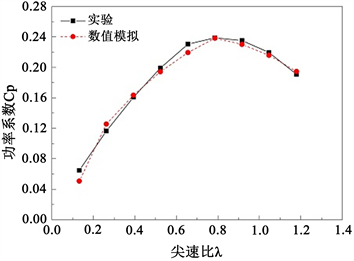
Figure 4. The validation of the turbulence model
图4. 湍流模型验证
为验证所选计算策略的可靠性,本文选取了传统两叶片Savonius风力机进行了数值模拟,计算了不同尖速比下风力机的功率系数,并和文献 [20] 实验结果进行对比,结果如图4所示。由图可见,在不同尖速比下,数值模拟结果与实验结果基本吻合。故本文选取的计算模拟策略适用于阻力型风力机的研究,所得出的结果具有较高的可靠性。
4. 计算结果分析
4.1. 叶轮功率特性
4.1.1. 最大弯度值的影响
图5给出了固定最大弯度位置(p)取值时不同最大弯度(m)对风力机性能的影响,图中也包括了传统型风力机的功率系数Cp随叶尖速比λ变化的关系图。从图5(a)中可以看出:当p = 0.4且弯度为0.3和0.4时,风力机的功率系数较大,且明显高于传统型Savonius风力机叶轮;其中,3040型风力机在尖速比λ为0.6时,取得最大功率系数为0.2357。当弯度值超过0.4后,随着弯度值的增加,风力机的性能随之下降,且当弯度值等于0.6时,6040型风力机效率明显低于传统Savonius风力机的效率。图5(b)显示,当p = 0.5时,3050、4050和5050型风力机的功率系数均高于传统Savonius风力机;随着弯度值的增加,风力机的最大功率系数逐渐降低,当弯度值为0.6时,其最大功率系数明显小于传统Savonius风力机的最大功率系数。由图5(c)发现,当弯度值为0.4时,4060型风力机在尖速比1.0处取得最大功率系数;当尖速比小于0.8时,3060 (弯度值0.3)、4060 (弯度值0.4)型风力机与传统Savonius风力机的功率系数随尖速比变化的曲线差异很小;但当尖速比大于0.8后,3060型和4060型风力机的功率系数均高于传统型风力机的功率系数。而6060型风力机(弯度值为0.6)最大功率系数则明显低于传统Savonius风力机的功率系数。总体而言,随着弯度的增大,Savonius叶轮的功率系数逐渐降低。还有一点值得注意的是,基于NACA翼型的风力机的工作范围均得到扩大,且在尖速比较大时的效率要高于传统Savonius风力机的效率。
4.1.2. 最大弯度位置的影响
图6给出了在最大弯度值相同时,最大弯度位置对功率系数的影响曲线。由图6(a)可知,随着最大弯度位置由0.4增加到0.6,风力机的效率逐渐降低,但该弯度值下的风力机取得的效率均高于传统Savonius风力机,且该类型的风力机在较高尖速比条件下取得较大功率系数。从图6(b)中看出,最大弯度位置的改变对于弯度值为0.4的风力机来说,影响不大。如图6(c)所示,在尖速比小于0.8时,弯度值为0.5的风力机和传统Savonius风力机的功率曲线无明显差异,当超过0.8后,该类型风力机取得的功率系数要高于传统型Savonius风力机,且在尖速比为1.4时最为明显。当弯度值为0.6时,该类型的风力机所获得最大功率系数明显低于传统Savonius风力机的最大功率系数,仅在尖速比为1.4时取得相对较高的功率系数。
4.2. 气动特性分析
为了分析该类型风力机取得较高功率系数的原因,本节对取得最大功率系数的3040型风力机和传统型Savonius风力机在尖速比0.8时的动态扭矩系数、流场和压力场进行了对比分析。
4.2.1. 动态扭矩系数及流动分析
图7为尖速比0.8时,3040型风力机和Savonius风力机的动态扭矩系数极坐标图。可以看出,3040型风力机的扭矩系数仅在小范围(120˚和300˚附近)出现了比Savonius风机的扭矩系数偏小的负值,而在120˚~180˚和300˚~360˚范围内,两者的值相差不大,但在0˚~90˚和180˚~270˚范围内均明显高出Savonius风力机的扭矩系数。因而,3040型风力机获得了更高的平均扭矩系数。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 5. The effects of different camber values on the power coefficient of the wind turbine
图5. 不同弯度值对风力机功率系数的影响
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 6. The effects of different camber positions on the power coefficient of the wind turbine
图6. 不同弯曲位置对风力机功率系数的影响
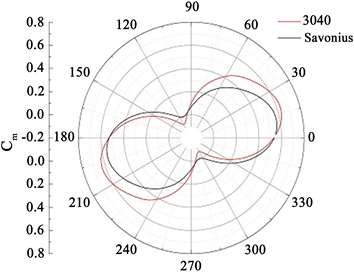
Figure 7. The polar diagram of dynamic torque coefficient
图7. 动态扭矩系数极坐标图
流体流过风力机内部产生的较大旋涡,是影响风力机效率的原因之一 [21] 。故本文选取了Savonius风力机和3040型风力机在相位角30˚时的流线图进行对比,如图8所示。由图可见,两者的回转叶片凹表面均产生一个较大涡旋,而后者的旋涡较小;同时,前者在迎风叶片前端和回转叶片后方均出现一个明显的小涡,而后者产生的旋涡则不明显。故3040型风力机流场内部涡旋的减少和尾流区涡旋的改善,促进了风机的旋转,从而提高了风力机的功率从输出。
 (a) Savonius风力机
(a) Savonius风力机  (b) 3040型风力机
(b) 3040型风力机
Figure 8. Streamlines of the wind turbines
图8. 风力机流线图
4.2.2. 压力场分析
图9分别给出了θ = 30˚时Savonius和3040风力机的迎风叶片和回转叶片表面的压力分布曲线,其中,转轴中心为坐标原点。图10给出了两种风力机周围的压力分布云图。由图9(a)可见,两者的迎风叶片凹表面的压力分布基本相同,而3040型叶轮迎风叶片凸表面的压力明显小于Savonius叶轮,该结论与图10中两种风力机的压力分布相对应,即3040风力机叶片凸表面的附近的低压面积要大于Savonius风力机的低压面积。由图9(b)可见,3040风力机回转叶片部分表面(距转轴中心−0.01~0.03的区间)的压差大于Savonius风力机的压差,而在叶片距转轴中心0.03~0.10的区间,其回转叶片表面的压差是较小的,这与图10(b)中回转叶片周围的压力分布相对应,即3040风力机在靠近转轴的回转叶片凸表面存在相对较高的压力分布,而在回转叶片的其他部分的压差较小,有利于风力机的转动。值得注意的是,3040风力机回转叶片的内部无明显低压区。因此,总体导致两叶片间的推动压差增大,使得3040风力机在30˚时取得较高的动态扭矩系数(见图7)。
 (a) 迎风叶片
(a) 迎风叶片  (b) 回转叶片
(b) 回转叶片
Figure 9. The distribution of pressure on the surface of Savonius and 3040 wind turbines, advanced blade (a); and returning blades (b) at θ = 30˚
图9. θ = 30˚时Savonius、3040型风力机迎风叶片(a) 和回转叶片;(b) 表面的压力分布
 (a) Savonius风力机
(a) Savonius风力机  (b) 3040型风力机
(b) 3040型风力机
Figure 10. Pressure contours of Savonius and 3040 wind turbine at θ = 30˚
图10. θ = 30˚时Savonius、3040型风力机压力分布云图
5. 结论
本文基于NACA翼型提出了新型Savonius风力机,并采用MATLAB参数化和非定常数值模拟方法对不同叶片形状进行了研究分析,结果表明:
1) 基于NACA翼型的Savonius风力机能够有效提高风力机的效率,其中3040型垂直轴风力机在尖速比为0.6处功率系数最佳为0.2357,比传统Savonius风力机功率系数高7.68%,且大部分基于NACA翼型的Savonius风力机的工作尖速比范围明显加宽。
2) 相比于最大弯度位置对基于NACA翼型的Savonius风力机效率的影响,弯度值的变化对功率系数影响较大。
3) 基于NACA翼型的叶型能够有效改变风力机周围的流场,增大风力机的推动压差,减弱叶型分离涡大小,从而提高风力机的效率。
NOTES
*通讯作者。