基于决策树算法与系统聚类的玻璃制品分类研究

Classification Study of Glass Products Based on Decision Tree Algorithm and System Clustering

摘要: 本文主要研究了古代玻璃制品的成分分析和鉴别，基于决策树算法建立玻璃分类模型，对63个文物样品进行分类，并对比分类结果与真实分类结果的吻合度，得出分类规律。在高钾无风化、高钾风化、铅钡无风化、铅钡风化的分类基础上，本文考虑基于系统聚类法对每个大类进行亚分类，并对分类后的结果进行合理性、敏感性分析，实现了对未知类型玻璃制品的鉴别以及各类型玻璃的亚类划分，对文物鉴别与玻璃制品分类有重要意义。

Abstract: This paper mainly studies the composition analysis and identification of ancient glass products, es-tablishes the glass classification model based on the decision tree algorithm, and classifies 63 cul-tural relic samples. The classification rule was obtained by comparing the agreement between the classification results and the real classification results. Based on the classification of high potassium weathering, high potassium weathering, lead-barium weathering and lead-barium weathering, this paper considers the sub-classification of each major category based on the systematic clustering method, the rationality and sensitivity of the results are analyzed, and the identification of un-known types of glass and the subclassification of different types of glass are realized.

1. 引言

古往自西汉的丝绸之路，今追至21世纪的“一带一路”，丝绸之路无疑为中西文化提供了沟通的渠道，其中玻璃则是则是早期贸易的见证者之一，它自西方传入我国后，又经过我国本土化制作，虽然外形相似，但化学成分依然有所不同。玻璃主要化学成分为二氧化硅，因其熔点高，需要加入助溶剂，根据添加的助溶剂种类，我国古代烧制出铅钡玻璃和钾玻璃。但因古代玻璃容易受到埋藏环境影响逐渐风化，使得其比例成分发生变化，让后人对其类别的分辨变得困难 [1] 。因此本文构建基于决策树算法与系统聚类的分析模型，根据现有相关数据对玻璃制品分类研究，以期为文物鉴别与玻璃制品研究领域提供一定的借鉴意义。

2. 数据的获取及假设

本文所用数据均来源于2022年高教社杯全国大学生数学建模竞赛C题。为了便于问题的分析，本文对所用数据做出以下假设：1) 假设文物的成分比例累加和介于85%~105%之间的数据视为有效数据；2) 假设不考虑时间及其他环境因素对化学成分含量变化的影响；3) 假设检测到的数据均为准确数据；4) 假设分类时不考虑颜色、纹饰等表象因素。

3. 基于决策树算法的玻璃分类模型的建立

3.1. 理论准备

决策树算法是一种机器学习算法，按照特征属性将对象进行分类，工作原理与人类的经验判断类似。按照规则对数据集中信息熵最高的特征进行分割，以此类推，进行分类，模型可读性高，计算量小，分类速度快 [2] 。

决策树采用自顶向下的树形结构，树的最顶层节点是该决策树的根节点，每一个内部节点代表数据的一个属性，每一个分支代表一个测试路径，每一个叶子节点代表一种分类，在决策树的内部节点进行属性的比较，并根据不同属性判断从该节点向下的分支，在决策树的叶节点得到结论。把决策树当成一个布尔函数，函数的输入为物体或情况的一切属性，输出为“是”或“否”的决策值。在决策树中，每个树枝节点对应着一个有关某项属性的测试，每个树叶节点对应着一个布尔函数值，树中的每个分支，代表测试属性其中一个可能的值。决策树分类算法通常分为两个步骤，决策树生成和决策树剪枝。

3.1.1. 决策树生成

构造决策树的方法是采用自上而下的递归构造，构造的结果是一棵二叉树或多叉树。以多叉树为例，它的构造思路是：以代表训练样本的单个结点开始建树，如果样本都在同一个类，则将其作为叶子结点，节点内容即是该类别标记。否则，根据某种策略选择一个属性，按照属性和各个取值，把例子集合划分为若干子集合，使得每个子集上的所有例子在该属性上具有同样的属性值。然后再依次递归处理各个子集。

3.1.2. 决策树剪枝

由于数据挖掘的对象是现实世界的数据，这些数据不是完美的，可能缺少必须的数据而造成数据不完整，或者数据不准确、含有噪声甚至是错误的，所以要讨论噪声问题。剪枝是一种克服训练样本集数据噪声的基本技术，对树进行修剪优化时要准确理解分类的特征描述和防止过多的噪声影响，从而达到更好的修剪效果，在确保精确程度的同时，提高可理解性。常用的剪枝技术有前期剪枝和后期剪枝，前期剪枝技术主要用来限制决策树的充分生长；后期剪枝技术则是待决策树充分生长后再进行剪枝。

1) 前期剪枝

前期剪枝最直接的方法有两种：第一、事先指定决策树生长的最大深度，决策树生长达到指定深度后则不再继续生长；第二、事先指定样本量的最小值，结点所含样本量不应小于该值，否则相应结点不能继续分支。

前期剪枝的优点是，操作简单，可以更快的完成模型的生成，适合对大数据集的处理。然而缺点是，前期剪枝在过滤掉无用数据的同时，有可能会过滤掉有用的数据，即决策树在不应该停止的时候停止构建，因此前期剪枝实际应用效果要略差于后期剪枝。

2) 后期剪枝

后期剪枝技术在允许决策树充分生长的基础上，根据一定的规则由下向上从树的叶子开始剪枝，逐步向根的方向剪，剪去决策树中那些不是一般性的子树，是一个边修剪边检验的过程。用户可以事先指定一个允许的最大误差值，剪枝过程将不断计算修剪当前决策子树对输出变量误差的影响。当误差大于允许的最大值时，则应立即停止剪枝，否则继续剪枝。基于训练样本集的后期修剪技术并不恰当，原因在于决策树是在训练样本集基础上建立的，较为合理的做法是利用测试样本集评价决策树的剪枝效果。当决策树在测试样本集上的错误率明显增大时，应停止剪枝。

3.2. 研究方法与结果分析

基于63个有效数据，本文借助决策树算法，搜索特征属性，根据特征属性即氧化铅的含量将所有文物样本分为两类，将氧化铅含量小于5.46的文物样品划分为第一类；将氧化铅含量大于等于5.46的文物样品划分为第二类。决策树模型如图1，分类完成后，借助Matlab完成了决策树算法的分类结果与实际分类结果的对比分析，结果如图2。

根据统计结果，分类结果吻合度对比准确率100%，证实了分类方法的合理性。经上述分析，高钾玻璃和铅钡玻璃的分类依据应为文物样本中氧化铅的含量，若氧化铅含量大于等于5.46，则文物样本属于铅钡玻璃，反之，属于高钾玻璃。

4. 基于系统聚类算法的亚分类模型的建立

4.1. 理论准备

系统聚类算法的基本思想是：按照距离远近，将距离相近的变量先聚成类，距离较远的变量后聚成类，依次进行，直到每个变量都归入合适的类中 [3] 。

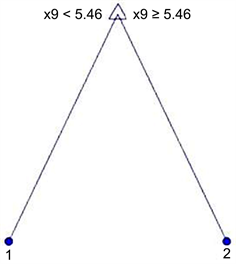
Figure 1. Decision tree classification model

图1. 决策树分类模型

Figure 2. Comparison between decision tree algorithm classification and real classification results

图2. 决策树算法分类情况与真实分类结果对比图

以n个样本的聚类分析为例，系统聚类法的步骤如下：

1) 定义以变量或指标的个数为维度的空间里的一种距离；

2) 计算n个样本两两之间的距离；

3) 将每个样本归为一类，根据计算出的样本间的距离合并距离最近的两类为一个新类；

4) 再计算新类与其他各类的距离，同样再根据计算出的距离合并距离最近的两类为一个新类；

5) 循环以上过程直至类别个数为1；

6) 画出各阶段的聚类图并决定类别的个数 [4] 。

4.2. 对分类指标的降维处理

玻璃分为铅钡玻璃及高钾玻璃,这两类玻璃均可进一步分为表面风化及无风化玻璃。首先计算出四种类别分别对应的各元素含量的标准差，选取离群数据即标准差较大的数据所对应的化学成分为分类指标，因为这类数据具有波动性大的特点，能很好地反映类与类之间的差异性，而其他化学成分因数据不足或波动较小，不予考虑 [5] 。

因此，在对高钾无风化类玻璃的亚类划分中，本文选取二氧化硅为分类指标；在对高钾风化玻璃的亚类划分中，本文选取二氧化硅为分类指标；在对铅钡无风化玻璃的亚类划分中，选取氧化铅、二氧化硅、氧化钡为分类指标 [6] ；在铅钡风化玻璃的亚类划分中，选取二氧化硅、氧化铅为分类指标。

4.3. 基于系统聚类的玻璃亚分类

应用系统聚类算法，本文先将所有文物样品看成一类，然后规定类与类之间的距离，采取欧式距离选择距离最小的一对合并成新的类，计算新类与其他类之间的距离，再将距离最近的两类合并，如此下去，直至所有的样品合为一类为止 [6] [7] 。

首先通过SPSS绘制出四种类别玻璃分别系统聚类所得谱系图如图3~6。

为了确定分类的类别数，本文依据聚合系数，做出了四种类型玻璃的聚合系数折线图。聚合系数定义如公式(1)

${{\displaystyle {\sum }_{k=1}^K{\displaystyle {\sum }_{i\in C_K}\left|x_i-u_k\right|}}}^2$ (1)

其中，u_k为各类中心的位置，C_k表示第k个类。聚合系数即各类的畸变程度之和。依据肘部法则，我们可以通过聚合系数折线图(也称肘形图)确定最佳分类数。最终将高钾无风化玻璃的亚分类数定为2；高钾风化玻璃的亚分类数定为2；铅钡无风化玻璃的亚分类数定为3，铅钡风化玻璃的亚分类数定为3 [8] 。

本文将最终的分类结果以散点图的形式进行可视化，如图7~10。

根据散点图，我们可以将高钾玻璃进一步分为低二氧化硅和高二氧化硅玻璃；将铅钡无风化玻璃进一步分为低硅低铅，低硅高铅和高硅低铅玻璃；将铅钡风化玻璃进一步分为低硅低钡高铅、低硅高钡低铅、高硅低钡低铅玻璃。

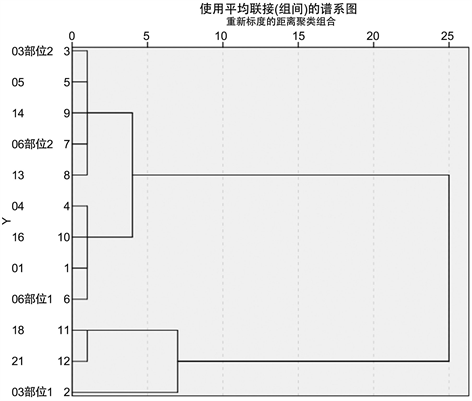
Figure 3. Sub-classification pedigree of high-potassium non-weathering glass

图3. 高钾无风化玻璃亚分类谱系图

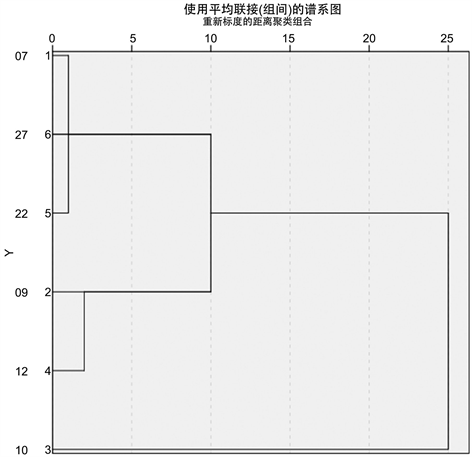
Figure 4. Sub-classification Pedigree of high-potassium Weathered Glass

图4. 高钾风化玻璃亚分类谱系图

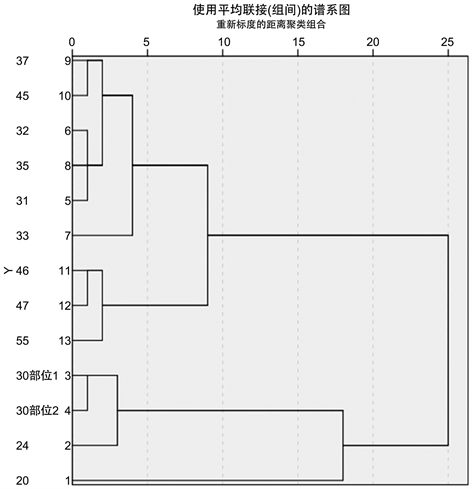
Figure 5. Subclassification pedigree of lead-barium unweathered glass

图5. 铅钡无风化亚分类谱系图

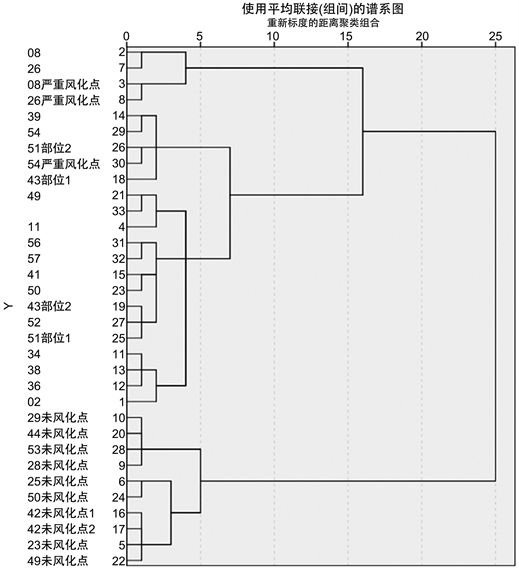
Figure 6. Subclassification pedigree of lead-barium weathered glass

图6. 铅钡风化亚分类谱系图

Figure 7. Scatter map of high potassium weathering sub-classification

图7. 高钾无风化亚分类散点图

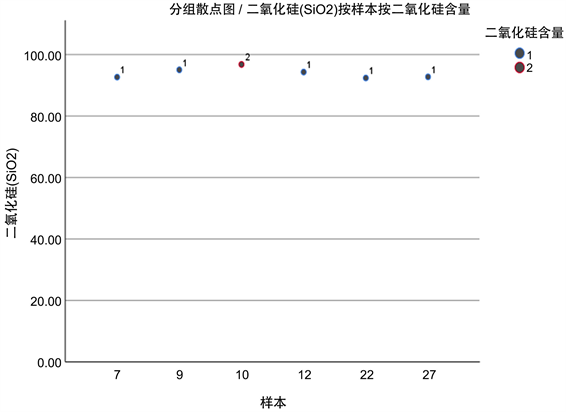
Figure 8. Scatter map of high potassium weathering sub-classification

图8. 高钾风化亚分类散点图

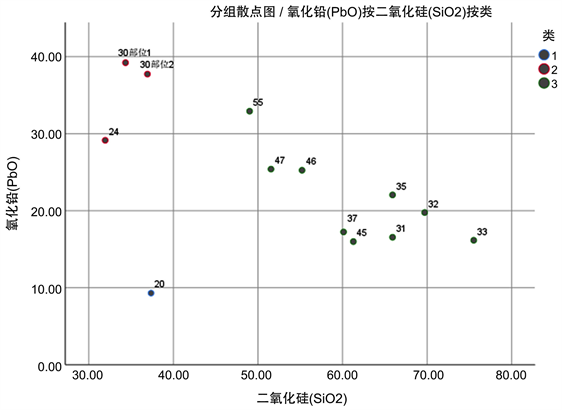
Figure 9. Scatter diagram of lead-barium weathering sub-classification

图9. 铅钡无风化亚分类散点图

模型选取波动大的化学成分作为分类指标，以类间距为分类标准，具有合理性。现以铅钡无风化的亚分类结果为例，如果将编号为30的文物划分为第三类，可以看出，30编号文物的二氧化硅含量为36.93，明显低于第三类二氧化硅含量的平均值61.58；氧化硅含量为37.74，明显高于第三类二氧化硅含量的平均值21.26，显然分类不准确，所以本分类模型具有合理性。

以铅钡无风化的亚分类结果为例，本文对此进行相应的敏感性分析。选取编号为24的玻璃文物，为其二氧化硅的含量增加1%的扰动，重新聚类得到对比结果如图11、图12，由此可以得出这种亚类划分模型是可靠的。

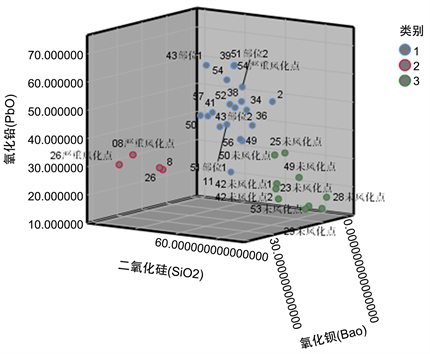
Figure 10. Scatter map of lead and barium weathering sub-classification

图10. 铅钡风化亚分类散点图

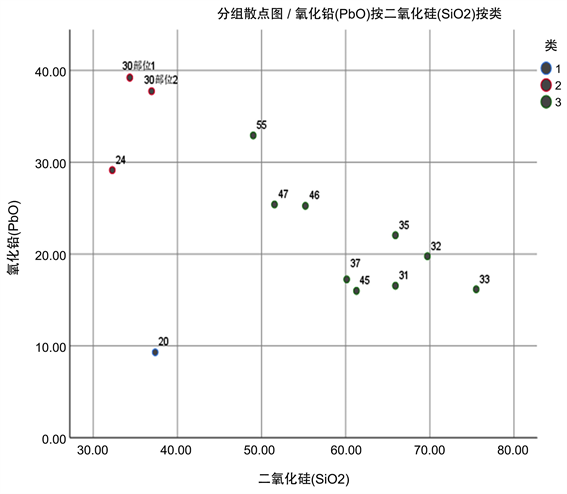
Figure 11. Scatter diagram of cluster analysis after disturbance

图11. 扰动后聚类分析散点图

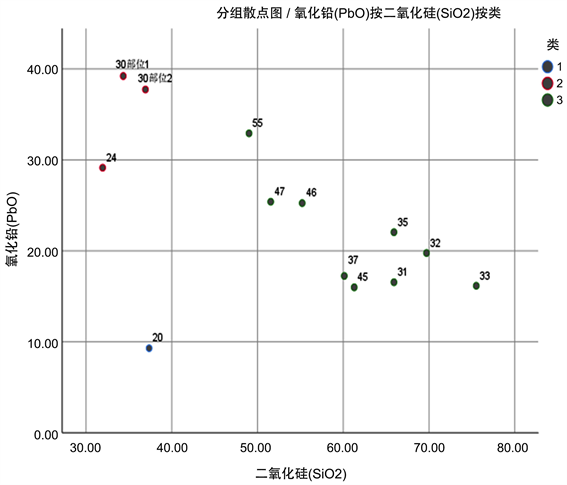
Figure 12. Scatter diagram of cluster analysis before disturbance

图12. 扰动前聚类分析散点图

5. 结语

玻璃制品成分鉴别与分类对于文物鉴别领域意义重大，本文基于决策树算法分析铅钡玻璃、高钾玻璃分类规律，建立玻璃分类模型对63个文物样品进行分类，并对比分类结果与真实分类结果的吻合度，得出分类规律 [9] 。在高钾无风化、高钾风化、铅钡无风化、铅钡风化的分类基础上基于系统聚类法对每个大类进行亚分类，并对分类后的结果进行合理性、敏感性分析，得到的划分模型精确度较高，对文物鉴别与玻璃制品分类研究领域具有一定的借鉴意义，但本文仅以各化学成分含量作为依据，以玻璃类型作为目标，并未考虑其他影响因素，还需要进一步分析各化学成分之间的相关性以及其他影响因素对最终结果的影响。