1. 引言
无人机(Unmanned Aerial Vehicle, UAV)目前在灾后救援、敌情侦察、航空摄影、监视测绘等领域的应用十分广泛,其定位技术的研究进展十分迅速,从初期的无人机集群思想的提出,到目前的前端算法技术主要有基于轻型卷积神经网络 [1] 、群峰编队方法 [2] 等。
本文采用纯方位法,即侧向法 [3] 进行无源定位,此方法仅仅使用发射信号的无人机给出的角信息,进行跟踪。在各个无人机相对位置不变的条件约束下,形成圆形编队在同一高度上飞行,由于高度不变此时的模型可以假定在二维平面内,不考虑多架飞机之间的俯仰角。接收信号无人机得到的方向信息为该无人机与任意两架发射信号无人机连线间的夹角。
当位于圆心的无人机和另外两架无人机发射信号时,此时可以假定以另两架无人机中其中一架和位于圆心的无人机的连线在X的正半轴,建立二维坐标系,利用几何模型求出各方位角角度与连线长度,得到其余位置略有偏差的被动无人机定位模型。
假设有9架无人机编号为FY00~FY08,其中FY00处于圆心位置,其余无人机按编号从小到大,逆时针均匀分布在圆外。FY00和FY01被选为发射信号,采用蒙特卡罗模拟方法,因为被接收信号无人机的方向角度信息已知,所以不妨采用伪随机数来构造接收到的角度信息,针对还需要几架的问题,可以通过计算关联精确度预测出发射信号的无人机架数,如果是还需要一架无人机,则针对3架发射信号无人机进行模拟检验,被接收信号无人机选择FY09,而第三个发射信号,可以采用定位模型思路对FY02~FY08进行遍历计算,比较计算的角度结果,观察误差情况。如果3架发射误差非常小,结论是还需要一架无人机发射信号;反之进行对比实验,比较不同架数得出误差值,选取最优的调整方案。
最后实际飞行中受导航精度等因素影响,需搜集资料进行计算,无人机集群朝统一方向运动,且每个个体都具有相同的运动特性则针对锥形集群调整无人机位置,可采用领导–追随者模型进行分层调整,保证机群的稳定。
2. 无源定位几何模型的建立与分析
2.1. 模型的假设
假设无人机可从系统中获得的高度信息,能够位于同一个高度上飞行,此时建立二维模型,不考虑两台无人机的俯仰角。同时无人机收到信号时间较短,此时对于时间误差忽略不计,运动轨迹的波动不会出现明显异常。
在无人机的飞行过程中,假定发射信号的无人机是相对静止的,无人机发生偏差时,在二维空间内仅考虑角度与距离的偏差。对于发射信号的无人机具有良好的稳定性与灵敏度,发射的方位信息准确无误,且自身的偏差可忽略。在编队中的无人机都有各自的编号,不考虑编号重复或编号中断的情况(图1)。

Figure 1. Drone formation and receiving direction infographic
图1. 无人机编队及接收方向信息图
2.2. 主要符号与说明(表1)

Table 1. Main symbols and descriptions
表1. 主要符号与说明
2.3. 基于正弦定理的几何模型
通过连接发射与接收的无人机,画出几何图形,进一步分析后分别建立图2两个几何模型:四边形模型与内接三角形模型。假设选取FY00,FY01,FY05三架飞机进行举例,组成夹角为160˚可以最大化涵盖两端被接收信号的无人机,因此具有普适性。此时位于中心的无人机和另外两架无人机能发射信号且位置无偏差,因此假设这三架无人机彼此之间方位角固定已知。此时任一被动接收信号的无人机能得到它与这三架飞机的方向信息,故可认为这一架无人机与另外三架中任意两架无人机所构成的方位角夹角已知,分别设为
。
为了确定待测无人机的位置,不妨设两个模型中无人机连线的两个待测角分别为y1,y2。通过模型求解出这两个角对待测无人机和发射信号无人机之间的相对方位进行定位。
在建立的四边形模型当中,对三个无人机所在点连线构成的内角所对的圆周上的三个无人机进行定位;此时由FY00,FY01,FY05连线构成的内角为160˚,令x为FY00与FY03连线,且三点连线构成钝角等腰三角形,再与单一被测无人机连线构成四边形。不妨以03、05号被测无人机为例进行分析。
 (a)
(a)  (b)
(b)
Figure 2. Schematic diagram of quadrilateral and inscribed triangle models
图2. 四边形和内接三角形模型示意图
由正弦定理可得出已知角度、待测角度和半径之间的关系:
(1)
同时由三角形内角和定理与四边形内角和定理得出:
(2)
由这一组关系推导出方程:
(3)
得到y1,y2的解,结合三角形内角和定理可得四边形模型当中各方位角,结合半径可得无人机各点连线长度,从而对被测无人机与发信无人机的相对位置进行定位。
在图2建立的内接等腰三角形模型中,对三个发送信号的无人机构成的外角所对圆周上的四个无人机进行定位,该情况与四边形类似。与三个无人机构成的等腰三角形一起构成了一个内接等腰三角形的大三角形:
(4)
同时我们由三角形内角定理和补角定理得出:
(5)
由上述关系可得出方程:
(6)
此时即可得到y1,y2的解,结合三角形内角和补角定理可得内接等腰三角形模型当中各方位角角度,已知半径可得无人机各点连线长度,从而对被测无人机与发信无人机之间的相对位置进行定位。
3. 运动多目标无源定位算法研究
利用两架无人机间的夹角关系测量的无源定位,是仅利用方位角作为指标,而发射与接收信号的无人机之间的距离信息不能直接观测,在二维坐标系内只能通过间接方法获得,方向信息与状态变量通常成非线性关系 [3] ,可以使用滤波等方法来取得统计最优的状态估计结果。此外,纯方位无源定位是一个最优非线性估计问题。
假设接收信号的无人机位置为
,则发送信号的无人机位置则是
,则发送信号的无人机和接收信号的无人机之间的关系有
用
表示真实值向量。根据侧向角交叉定位原理 [4] ,可估计被动接收信号的定位模型,估计此时被动无人机所在位置:
(7)
式中
由于加权最小二乘法定义权矩阵
,AOA无源多目标定位公式如下:
(8)
由上可推出
3.1. 运动多目标无源定位算法的求解
发射信号的无人机与被动接收信号的无人机距离为:
遍历当前所有的连线,计算
目标位置与当前连线的关联精确度;根据发射无人机发送的不同位置信息,运用最小二乘法解出收到信号的无人机位置,将方位角和目标位置进行关联 [4] ,可得到关联精确度如表2所示。

Table 2. The accuracy of the correlation between transmitting and receiving drone signals
表2. 发射与接收无人机信号的关联精确度
由表2我们可以得出当发射信号的无人机架数为3架时,关联精确度最高。随着发射信号的无人机架数的增加,关联精确度呈下降趋势。
3.2. 运动多目标无源定位模型建立
根据3.1得出的结论,针对3架发射信号无人机进行模拟检验,基于建立的正弦定位模型思路,将几何关系的定位思想贯彻其中,并进行调整建立3种具体的定位模型,对于无人机的位置偏差假设主要采用的是蒙特卡罗模拟方法。然后通过matlab和excel等软件对数据进行计算与整理,从而达到对无人机有效定位的目的,其中蒙特卡罗模拟的计算成本也是比较低,并从结果上可以分析出角度偏差非常微小,计算精度也是符合要求的。
选择FY09作为被接受信号无人机,然后固定FY00和FY01为发射信号,第三个发射信号随机选取。针对第三个发射信号的不同,从而对应的几何关系与定位模型的具体化,将每一种情况进行了模型归类。
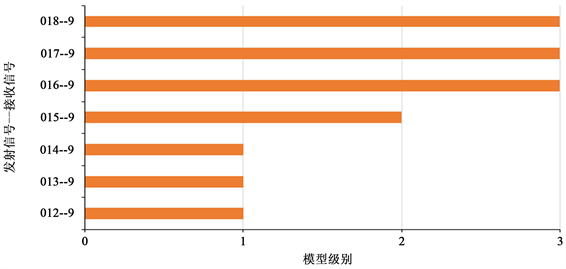
Figure 3. Locate model-level classifications
图3. 定位模型级别分类情况
图3定位模型级别分类情况,其中0、1、7~9的含义是发射信号为FY00、FY01、FY07,被接收信号为FY09;对应的模型级别为3,三种模型级别对应了三种不同的几何关系图,运用几何模型的思想即可求解;图4理想方位角信息,对每一组进行一个标准计算,即假设被接收信号无人机无位置偏差,进而求出对应准确无误的方位角特征信息。
3.3. 运动多目标无源定位模型有效性检验
使用matlab软件,进行蒙特卡罗模拟,求解出结果并分析误差变化。假设每个发射信号无人飞机的位置偏差为 ± 1˚变化,即在标准方位角信息上下浮动1˚,均匀分布取十个进行模拟,并带入对应的定位等级模型1、2、3中进行检验。其中第十一个数据为带入无位置偏差时的方位角信息,从而进行对比,分析出定位模型的有效性。
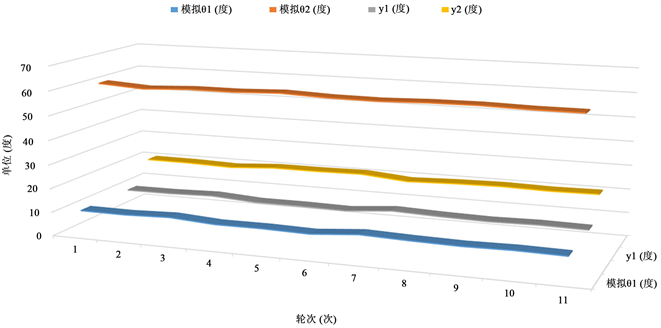
Figure 5. Effects and comparison of Monte Carlo simulation of position deviation
图5. 蒙特卡罗模拟位置偏差的效果与比较
从图5模拟结果来看,3架无人机发射信号的误差性非常小,不再采取4架无人机进行对比仿真实验,并且各个定位模型等级都有良好的定位效果,偏差也在接收范围之内,故3架无人机发射信号即可。
4. 无源定位几何构型控制
4.1. 基于图论原理的集群算法设计
无人机集群向某一特定位置飞行需保持编队队形,通过建立一个领导–追随者模型,其优点在于队形的遂行问题可以直接由领导者实现,在不需要每架无人机都能接收到多位领导者发出的信息的情况下,实现纯方向无源定位。我们把无人机的个体简化为一个质点,基于一致性控制协同算法将重点放在无人机集群 [5] ,假设无人机集群朝同一方向运动,且在无人机集群的每个个体都具有相同的运动特性。
从结论可知以三架无人机为发射信号源的性能最优,在实际情况中,无人机集群在规避障碍时,以无人机的期望间距为边和方位角构成的三角形编队的集合构型几何构型最为稳定 [5] ,初步设定以下两种领导–追随者模型构建方式(图6)。
(9)
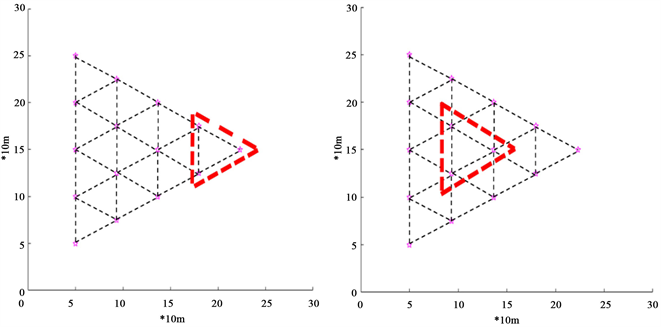
Figure 6. Two ways to build a leader-follower model
图6. 两种领导–追随者模型构建方式
式中:
为无人机i的初始位置;
为无人机i的方位角;无人机i的实际输入量为速度
和角速度
。
假设无人机的模拟输入为
,建立实际输入量的方程组:
(10)
无人机之间的方向信息传递是由发射信号的领导无人机传递,只能接收信号的跟随无人机,根据图论原理,假设图G有关的矩阵为邻接矩阵A、主对角D和拉普拉斯矩阵L = D − A,为无人机编队方向信息的集合则以三架无人机为一个整体,无人机集群可从第i个整体中得到相关方向信息。当(j, i)这一通信路径属于无人机编队的集合时,
为1,反之则为0。
即邻接矩阵:
(11)
按照上至下,从左至右的顺序,对跟随无人机进行编号
,领导无人机编号为n + 1,则此时基于图论原理采用的方向信息交互G就变为了:
(12)
在飞行过程中,每台无人机与相邻无人机之间的相对距离为50 m,当领导者的运动轨迹发生改变时,接收信号无人机都会根据领导者运动轨迹改变的方向进行调整
4.2. 一致性算法的求解
领导者的运动方向是每个跟随者的目标位置,
设定是无人机期望保持的间距 [6] 。
构建二维旋转矩阵,可以列出以下等式:
(13)
其中
是无人机的纯方位角,利用无人机集群协议可得到(表3)
(14)

Table 3. The best fitting angle for passive localization clusters
表3. 无源定位集群的最佳拟合角度
以下是给出的无人机调整方案,在15架无人机编队调整初期,锥形三个顶点处的红色实线围出的三架无人机构成三角形,并发射方向信号用来控制15架无人机集群的整体行进方向,起到定位和控制锥形构型的作用(图7)。
其次位于15架无人机集群中心的红色发射方向信号,这三架无人机中每架无人机都可以与蓝色绿色实线表示跟随无人机构成三角形,集群呈0˚~90˚~270˚构型保证了锥形中被动接受信号的无人机集群的稳定性,不会在小范围内产生位置偏差。被动接收信号的无人机为绿色,橙色的无人机,最后进行位置调整(图8)。
针对在无人机集群中由于只接收相邻位置的无人机的位置信号可能会产生分块现象 [7] ,我们建立了以下模型,保证无人机在第一层级被两两控制,第二层级被中心发射信号的无人机控制,有效避免了分块现象(图9)。
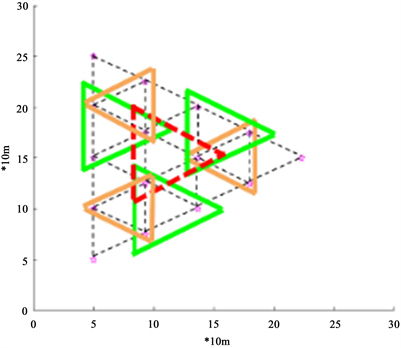
Figure 8. UAV position adjustment scheme
图8. 无人机位置调整方案
5. 结论与展望
模型的计算采用专业软件求解,例如matlab软件,分析得到的数据可信度较高,建立的模型能够与飞行情况紧密联系,结合实际情况使得模型具有很好的通用性和推广性。
但是模型仍具有一定缺陷:实际过程中,当无人机机群沿一定飞行轨迹移动时,飞行轨迹若是直线,则相对可能产生的误差较小,若无人机集群转变方向,则产生的可能误差较大;此外,若考虑俯仰角对无人机集群的影响,模型将会更为精确;目前无人机主要用于执行某些特殊任务,对技术的要求高,当执行某些特技动作时,自身的状态量会发生改变,未考虑气流对模型的影响。
考虑到在实际应用中,无人机集群各个无人机的俯仰角之间会对领导–跟随模型有影响,故在模型上添加俯仰角参数进行改进,加入俯仰角后,需要重新计算关联精确度、距离等参数。俯仰角的增加,将会使得模型从二维变至三维,相关方程组也会增加,但定位效果将更加完善、可靠。