基于低碳低成本的联轴器工艺参数优化

Modeling and Optimization of Coupling Pro-cess Parameters Based on Low Carbon and Low Cost

摘要: 为了更有效地推动制造业减排，综合考虑机械切削加工过程中碳排放和加工成本的影响因素，提出针对联轴器的工艺参数优化问题。首先建立了切削加工过程中包含电能、刀具和切削液在内的碳排放函数和加工成本优化函数，在此基础上建立了以最小碳排放和最小加工成本为目标的加工工艺参数优化模型；其次，为提高万有引力搜索算法(Gravitational Search Algorithm, GSA)全局搜索能力，将自适应变异触发函数引入算法，同时将聚集度作为进行变异操作评价标准，提出了改进GSA算法，降低算法复杂度。最后，针对某型号的联轴器切削加工工艺，应用改进GSA算法搜索最优解，获取对应的最佳工艺参数。结果表明，采用改进GSA算法对平均碳排放量和加工成本分别降低了10.41%和13.81%，表明该优化方法可行、有效。该研究提出的模型方法和工艺参数优化方法可为数控机床制造选择合理的切削工艺参数提供理论指导。

Abstract: In order to promote the emission reduction of manufacturing industry more effectively, this paper comprehensively considers the influencing factors of carbon emission and processing cost in the mechanical cutting process, establishes the carbon emission function and processing cost optimiza-tion function in the cutting process, including electrical energy, cutting tools and cutting fluid, and on this basis, establishes the optimization model of processing parameters with the goal of mini-mum carbon emission and minimum processing cost; In order to improve the global search ability of Gravitational Search Algorithm (GSA), the adaptive mutation trigger function is introduced into the algorithm, and the aggregation degree is used as the evaluation standard for mutation opera-tion to reduce the complexity of the algorithm. Through an example, the improved GSA algorithm is applied to search the optimal solution and obtain the corresponding optimal process parameters. The results show that the average carbon emissions and processing costs are reduced by 10.41% and 13.81% respectively, which verifies the effectiveness and feasibility of the proposed optimiza-tion method. The model and method can provide theoretical support for selecting reasonable cut-ting parameters in NC machine tool manufacturing.

1. 引言

伴随着钢铁制造业的高速发展，温室气体排放量急速上升，全球气候变得愈发恶劣，人们开始探讨节能减排的可持续发展方式。“低碳制造”是目前国内外都较认可的一种新型制造模式，也是未来制造业的大方向 [1] 。实现低碳制造，关键在于减少生产制造过程的各个工序阶段物料能源消耗，提高加工效率和废料利用效益，降低碳排放量。因此，为了实现低碳制造，如何描述制造生产过程排放状况，并分析制造过程碳排放特性以及碳源分布流量、碳排放全过程变化规律，是当前迫切需要解决的科学问题之一 [2] 。

针对碳足迹量化计算问题，目前已有很多研究。郑楚威等 [3] 对滚齿加工做出碳排放定量优化分析，以时间为单位对滚齿加工进行分析，从而建立了批量生产的定量计算模型，同时使用遗传算法进行仿真分析，得到优化后的碳排放量。Hongming Na等 [4] 结合材料参数、工艺参数和反应条件为约束条件，以能源效率最大化为优化目标对典型ISMP进行优化，并进一步分析了典型ISMP的能耗和CO₂排放。Runying An等 [5] 设计了一种NET-IS模型来预测钢铁生产需求并选择满足钢铁需求的生产技术，计算能源消耗和CO₂排放。Jiaying Peng等 [6] 在研究中使用IO-SPA方法考虑到能源消耗带来的CO₂排放，识别出在供应链中所消耗某种类型的能源所推导出的排放量。上述研究从多种角度对碳足迹量化模型进行了研究，为建立低碳低成本的加工工艺参数优化模型提供了理论支持。

对于机加工切削工艺参数优化方面的研究，张如敏等 [7] 采用响应面法与遗传算法，以表面粗糙度为优化目标进行了切削参数优化。张楚锋等 [8] 采用回归分析法与遗传算法，研究了以能耗和成本最低为目标下的工艺参数优化问题。詹欣隆等 [9] 结合传统制造业切削参数优化与柔性作业车间调度优化，采用改进后的非支配排序遗传算法和离散化引力搜索算法对其提出的高效低碳车间改进算法进行比较分析，验证了改进引力搜索算法在该领域的适用性。李聪波等 [10] 在刀具磨损状态连续变化下，对面向能耗的数控车削批量加工切削参数优化问题进行了研究。上述研究主要从能耗和加工时间角度对切削加工碳排放进行估算与优化，但过度强调高效会导致主轴转速增加进而刀具损耗增加等，进而增加加工成本 [11] ，且这些研究主要采用传统的遗传算法求解，求解效率较低。

针对上述问题，本文综合考虑机床性能约束，建立了车削过程中以碳排放最低、加工成本最少为目标的工艺参数优化模型，最后运用改进的万有引力搜索算法(Gravitational Search Algorithm, GSA)对所建模型进行寻优求解，以实例验证所建模型的有效性。

2. 联轴器加工工艺参数优化模型建立

2.1. 优化变量确定

在数控切削加工过程中，合理制定加工工艺参数对高效低碳制造有着重要影响。切削速度、进给量和背吃刀量是切削用量三要素。因此本文设定优化变量为主轴转速n、工作台进给量f以及背吃刀量a_p。

2.2. 优化目标函数

本文研究的是基于绿色制造下的最大效益问题，如果将联轴器的切削加工成本以及切削碳排放进行优化，则能得到较高的切削碳效益。因此本文考虑低碳、低成本两个方面的因素，以减少加工成本和降低碳排放量为优化目标。

2.2.1. 切削加工过程碳排放函数

联轴器切削加工引起的碳排放主要途径有：1) 物料的切削用量；2) 机床消耗电能；3) 刀具磨损；4) 切削液使用；5) 其他辅助设备(公共场所照明、空调系统等)。其中前两个途径的碳排放量为加工工艺固定碳排放量，不会随着切削参数改变而改变或者变化甚微，可以认为是一个常量，因此本文以切削参数为优化变量，只考虑剩余途径的碳排放量。根据机床活动状态，本文从切削加工过程碳排放和机床空载碳排放考虑加工车间碳排放。

联轴器机加工过程的总碳排放可用式(1)计算：

$C_{\text{p}}=C_{\text{t}}+C_{\text{y}}$ (1)

其中：C_p为联轴器机加工产生的总碳排放量，g；C_t为联轴器生产过程中在切削加工工艺流程产生的碳排放量，g；C_y为机床空载时产生的碳排放，g。

1) 切削加工过程碳排放

机床在切削加工状态下所产生的碳排放C_t可分为两部分：电能消耗产生的碳排放和切削刀具、切削液产生的碳排放，可用式(2)和式(3)计算：

$\begin{array}{c}{C}_{\text{e}}=C_{\text{d}}+C_{\text{f}}\end{array}={\displaystyle \underset{k=1}{\overset{K}{\sum }}{F}_{\text{e}}\left(P_{\text{n}}+P_{\text{m}}\right)T_{\text{m}k}/60}$ (2)

$P_{\text{n}}=F_{\text{n}}{V}_{\text{n}}=C_{{\text{F}}_{\text{c}}}{a}_{\text{sp}}^{{\chi }_{F_{\text{c}}}}{f}^{y_{F_{\text{c}}}}{v}_{\text{c}}^{n_{F_{\text{c}}}}{K}_{F_{\text{c}}}{v}_{\text{c}}\times {10}^{-3}$ (3)

其中：C_e为电能消耗产生的碳排放，g；C_d为数控车床主传动系统的碳排放量，g；C_f为伴随切削加工过程中附加载荷能耗产生的碳排放量，g；F_e为电能碳排放因子，kgCO₂e/(kW·h)；P_n为切削功率，kW；T_mk为第k次切削加工时间，min；F_n为主切削力，N；C_Fc、x_Fc、y_Fc、n_Fc和K_Fc均为切削力计算相关系数，a_sp为背吃刀量，mm；f为进给量，mm；v_c为切削速度，m/s。

附加载荷功率P_m可通过切削功率计算 [12] ：

$P_{\text{m}}=c_{\text{n}}{P}_{\text{n}}$ (4)

其中c_n为附加载荷损耗系数，本文取c_n = 0.2。

刀具磨损的碳排放量计算公式为：

$C_{\text{h}}=\frac{T_{\text{m}}}{\left(N\text{+1}\right)L_{\text{t}}}{F}_{\text{m}}{f}_{\text{m}}\times {10}^3$ (5)

其中：C_h为刀具磨损的碳排放量，g；T_m为切削加工时间，min；N为刀具刃磨次数，L_t为刀具寿命，min；F_m为刀具材料碳排放因子，kgCO₂e/kg；f_m为刀片质量，kg。

在机械加工过程中，切削液的碳排放量主要考虑切削液制备使用以及废液的处理这两点。由切削液引起的碳排放可用式(6) [11] 计算：

$C_{\text{c}}=\frac{\left(T_{\text{m}}+T_{\text{Nlt}}\right)}{C_{\text{L}}}\left(C_{\text{pe}}+C_{\text{de}}\right)V\times {10}^3$ (6)

其中：C_c为切削液产生的碳排放量，g；C_L为切削液更换周期，min；V为切削液体积，L；T_Nlt为切削过程中的车床的空载时间，min；生产切削液碳排放因子C_pe和废液碳排放因子C_de分别取2.85 kgCO₂e/L和0.2 kgCO₂e/L [13] 。

2) 机床空载碳排放

机床在空载闲置时产生的碳排放C_y为：

$C_{\text{y}}={\displaystyle \underset{k=1}{\overset{\text{K}}{\sum }}{F}_{\text{e}}{P}_{\text{Mnlp}}{T}_{\text{Nlt}k}/60}$ (7)

其中：P_Mnlp为切削过程空载时的空载功率，kW；T_Nltk为第k次切削加工空载时间。

根据车床切削过程和空载碳排放，车间总碳排放量可通过式(8)计算：

$\begin{array}{c}{C}_{\text{p}}=C_{\text{e}}+C_{\text{h}}+C_{\text{c}}+C_{\text{y}}\\ ={\displaystyle \underset{k}{\overset{K}{\sum }}\left[\left(1+c_{\text{m}}\right)F_{\text{e}}{C}_{F_{\text{c}}}{a}_{\text{sp}}^{{\chi }_{F_{\text{c}}}}{f}^{y_{F_{\text{c}}}}{v}_{\text{c}}^{n_{F_{\text{c}}}}{K}_{F_{\text{c}}}{v}_{\text{c}}{T}_{\text{m}k}/\left(6\times {10}^4\right)+F_{\text{e}}{P}_{\text{Mnlp}}{T}_{\text{Nlt}k}/60\right]}\\ +\frac{T_{\text{m}}}{\left(N\text{+1}\right)L_{\text{t}}}{F}_{\text{m}}^3{f}_{\text{m}}^3\times {10}^3+\frac{\left(T_{\text{m}}+T_{\text{Nlt}}\right)}{C_{\text{L}}}\left(C_{\text{pe}}+C_{\text{de}}\right)V\times {10}^3\end{array}$ (8)

2.2.2. 切削加工过程成本函数

加工过程中的成本包括机床加工费用、刀具损耗费用和辅助系统能耗费用，其中机床加工费用可通过折旧费计算；辅助系统能耗主要和车间布置有关，与切削参数关系甚微，在本文中不计入考虑。

在切削加工过程中，根据刀具移动轨迹长度l_ck和数控机床设定的单位时间内刀具进给量f_ck估算出车削加工工艺中第k次切削的实际加工时间：

$T_{\text{m}k}=\frac{l_{\text{c}k}}{60\times f_{\text{c}k}}$ (9)

同理空载时间T_Nltk为：

$T_{Nltk}=\frac{l_{\text{em}k}}{60\times f_{\text{em}k}}$ (10)

其中：l_emk为空载时的刀具移动轨迹长度，m；f_emk为空载时的刀具移动速度，m/s。

机床加工费用为：

$G_{eq}=T_m+T_e+T_{Nlt}=\left({\displaystyle \underset{k=1}{\overset{K}{\sum }}\frac{l_{\text{c}k}}{f_{\text{c}k}}+{\displaystyle \underset{k=1}{\overset{K-1}{\sum }}{T}_{\text{e}k}}+{\displaystyle \underset{k=1}{\overset{K}{\sum }}\frac{l_{\text{em}k}}{f_{\text{em}k}}}}\right)\frac{R_{\text{mt}}}{60}$ (11)

其中：T_ek为第k次切削过程的换刀时间，min。

刀具损耗费用可通过切屑体积和刀具背吃刀量来计算。参考 [14] ，刀具损耗费用为：

$G_{ep}={\displaystyle \underset{q=1}{\overset{m}{\sum }}\frac{S^{(q)}{a}_p^{(q)}}{L_t^{(q)}{a}_p{a}_q}{C}^{(q)}}$ (12)

其中：S(q)、a_q、C(q)分别为第q个刀具切除的面积、轴向吃刀量和购买成本。

综上可知，机械加工总成本为：

$G_{\text{s}}=G_{\text{eq}}+G_{\text{ep}}=\left({\displaystyle \underset{k=1}{\overset{K}{\sum }}\frac{l_{\text{c}k}}{f_{\text{c}k}}+{\displaystyle \underset{k=1}{\overset{K-1}{\sum }}{T}_{\text{e}k}}+{\displaystyle \underset{k=1}{\overset{K}{\sum }}\frac{l_{\text{em}k}}{f_{\text{em}k}}}}\right)\frac{R_{\text{mt}}}{60}+{\displaystyle \underset{q=1}{\overset{m}{\sum }}\frac{S^{(q)}{a}_p^{(q)}}{L_t^{(q)}{a}_p{a}_q}{C}^{(q)}}$ (13)

2.3. 约束条件

在加工过程中，车削加工的功率不能超过最大功率P_max：

$\begin{array}{c}\frac{F_{\text{n}}{v}_{\text{c}}}{1000}\le P_{\max }\end{array}$ (14)

车削加工后的零件表面粗糙度需要达到相关工序要求的标准，因此车削加工相关参数也受到工件表面质量的约束：

$\begin{array}{c}Ra=\frac{1000f^2}{32r_{\text{g}}}\le R{a}_{\max }\end{array}$ (15)

其中：Ra和Ra_max分别为表面粗糙度和最大表面粗糙度；r_g为刀尖圆弧半径，mm。

数控车床的最大切削力F_max必须大于切削所需要的切削力：

$C_{F_{\text{c}}}{a}_{\text{sp}}^{{\chi }_{F_{\text{c}}}}{f}^{y_{F_{\text{c}}}}{v}_c^{n_{F_{\text{c}}}}{K}_{F_{\text{c}}}\le F_{\max }$ (16)

车床车削加工过程中，选用的车削参数必须符合车床的额定参数要求：

$n_{\min }<n<n_{\max }$ (17)

其中：n_min、n_max分别为最小主轴转速和最大主轴转速，r·min⁻¹。参考文献 [15] ，设待加工面直径为d，可得：

$\begin{array}{c}n=\frac{1000v_{\text{c}}}{\text{π}d}\end{array}$

其中：f_min和f_max分别为最小进给量和最大进给量，mm·r⁻¹。综上所述，以低碳低成本为目标的切削优化模型如下：

$\min F\left(n,f,a_{\text{p}}\right)=\left(\min C_{\text{p}},\min G_{\text{s}}\right)$

$\begin{array}{c}s.t.\frac{F_{\text{c}}{v}_{\text{c}}}{1000}\le P_{\max }\\ \frac{1000f^2}{32r_{\text{g}}}\le R{a}_{\max }\\ C_{F_{\text{c}}}{a}_{\text{sp}}^{{\chi }_{F_{\text{c}}}}{f}^{y_{F_{\text{c}}}}{v}_{\text{c}}^{n_{F_{\text{c}}}}{K}_{F_{\text{c}}}\le F_{\max }\\ n_{\min }<n<n_{\max }\\ f_{\min }<f<f_{\max }\end{array}$

3. 基于改进GSA的模型求解

3.1. 多目标函数转化

以降低碳排放和减少加工时间为目标的模型中含有两个待优化的非负目标函数，并且包含3个优化参数，很难寻找到目标函数最优解。因此本文采用权重系数法，将多目标函数转化为单目标函数：

$\min F\left(v,f,a_{\text{p}}\right)=\left(w_1\min C_{\text{p}},w_2\min G_{\text{s}}\right)$ (18)

其中：w₁、w₂分别为碳排放和加工成本相关的权重系数，通过模糊评价法确定w₁ = 0.5、w₂ = 0.5。

为避免碳排放目标函数和加工成本目标函数量纲不同，需要对目标函数进行量纲一化处理：

$C_{\text{p}}^{*}=\frac{C_{\text{p}}-C_{\text{p}\min }}{C_{\text{p}\max }-C_{\text{p}\min }}$ (19)

$G_{\text{s}}^{*}=\frac{G_{\text{s}}-G_{\text{s}\min }}{G_{\text{s}\max }-G_{\text{s}\min }}$ (20)

其中：C_pmax、C_pmin分别是碳排放函数在约束条件下的最大值和最小值，g；G_smax、G_smin分别是加工成本函数在约束条件下的最大值和最小值，元。

经处理后的单目标函数为：

$\min F\left(v,f,a_{\text{p}}\right)=\min \left(w_1\frac{C_{\text{p}}-C_{\text{p}\min }}{C_{\text{p}\max }-C_{\text{p}\min }}+w_2\frac{G_{\text{s}}-G_{\text{s}\min }}{G_{\text{s}\max }-G_{\text{s}\min }}\right)$ (21)

3.2. 基于改进GSA的加工工艺参数优化

GSA是RASHEDI等学者在2009年受万有引力的启发，提出的一种基于牛顿万有引力定律和第二运动定律的启发式智能搜索算法 [16] 。该算法根据物体与物体之间会在引力的作用下相互吸引的特质来构造算法，其实现简单，收敛迅速，并且具备较强的全局搜索能力。

3.2.1. 惯性质量计算

粒子i在t时刻相应的质量M_i(t)可表示为：

$M_i\left(t\right)=\frac{m_i\left(t\right)}{{\displaystyle \underset{j=1}{\overset{N}{\sum }}{m}_j\left(t\right)}}$ (22)

$\begin{array}{c}{m}_j\left(t\right)=\frac{f_{\text{fit}i}\left(t\right)-w_{\text{worst}}\left(t\right)}{b_{\text{best}}\left(t\right)-w_{\text{worst}}\left(t\right)}\end{array}$ (23)

其中：f_fiti(t)为粒子j在t时刻的适应度值；N为种群中粒子数。b_best(t)为t时刻粒子j搜索的最佳适应度值，w_worst(t)为t时刻粒子j搜索的最差适应度值，两者定义为：

$b_{\text{best}}\left(t\right)=min{f}_{\text{fit}j}\left(t\right)$ (24)

$w_{\text{worst}}\left(t\right)=max{f}_{\text{fit}j}\left(t\right)$ (25)

3.2.2. 万有引力计算

假设在一个D维的搜索空间中，随机产生一个初始种群，种群粒子个数为N。参考文献 [17] ，在t时刻，第j个施力粒子和第i个受力粒子之间的作用力F_dij(t)计算公式为：

$F_{dij}\left(t\right)=G\left(t\right)\frac{M_i\left(t\right)M_j\left(t\right)}{R_{ij}\left(t\right)+\epsilon }\left[x_{dj}\left(t\right)-x_{dj}\left(t\right)\right]$ (26)

$R_{ij}\left(t\right)={\Vert X_i\left(t\right),X_j\left(t\right)\Vert }_2$ (27)

其中：x为粒子所处位置；G为引力常数；ε为一个微小常量； $R_{ij}\left(t\right)$ 为t时刻受力粒子与施力粒子之间的欧氏距离。

粒子i受到的力F_di(t)可用式(28)计算：

$\begin{array}{c}{F}_{dj}\left(t\right)={\displaystyle \underset{j=1,j\ne i}{\overset{N}{\sum }}rand{\left(0,1\right)}_j{F}_{dij}\left(t\right)}\end{array}$ (28)

3.2.3. 粒子属性更新

d维空间中粒子在t时刻的加速度 $a_{di}\left(t\right)$ 表示为：

$\begin{array}{c}{a}_{di}\left(t\right)=\frac{F_{di}\left(t\right)}{M_i\left(t\right)}\end{array}$ (29)

粒子i的速度更新公式为：

$v_{di}\left(t+1\right)=rand{\left(0,1\right)}_i{v}_{di}\left(t\right)+a_{di}\left(t\right)$ (30)

结合式(30)可知当前粒子i所处位置为：

$x_{di}\left(t+1\right)=x_{di}\left(t\right)+v_{di}\left(t+1\right)$ (31)

3.2.4. 问题描述和算法改进

GSA算法简单实用，常用于处理非线性约束优化问题，但GSA算法在搜索最优解的过程中，很容易提前收敛，从而陷入局部最优解，降低实际应用的质量。而另一方面，遗传算法(Genetic Algorithm, GA)会通过使用交叉和变异这两步操作来提高每次迭代时种群的多样性，可以避免过早收敛。根据GA算法这一特点，本文提出了一种基于GA的改进GSA算法。该算法在求解粒子质量时增加了遗传算法中的粒子变异思想，不直接对粒子进行变异操作，而是在满足变异触发函数条件下，让粒子在合适范围内产生变异。由于每次迭代对所有粒子都会判断变异是否触发，算法执行效率低，因此引入聚集度理论，在种群多样性降低时进行变异。改进后具体操作步骤如下。

步骤1：种群初始化，随机产生粒子的位置，设置初始参数。

步骤2：计算粒子的适应度，记录最优值粒子位置，计算聚集度。

步骤3：如果δ_t – δ_t–1 > 0，执行步骤6。否则执行步骤4。

步骤4：根据变异触发函数表达式来判断粒子是否满足变异，符合条件的粒子进行正态变异操作。

步骤5：计算当前代最佳值b_best(t)和最坏值b_worst(t)，并由此求出和更新当前全局最优解的位置。

步骤6：求出粒子惯性质量，更新引力常数。

步骤7：计算粒子加速度。

步骤8：更新粒子速度和位置。

步骤9：返回步骤2循环迭代，直到符合迭代要求的次数后停止迭代。

步骤10：结束循环，输出结果。

步骤2第t代粒子的聚集度，其计算公式为：

${\delta }_t=\frac{1}{N}\underset{i=1}{\overset{N}{{\displaystyle \sum }}}\left|\frac{f_{\text{fit}i}\left(t\right)-f_{\text{avg}}\left(t\right)}{b_{\text{best}}\left(t\right)-w_{\text{worst}}\left(t\right)}\right|$ (32)

其中：δ_t为第t代粒子适应度平均值。

由式(32)可知，当δ_t越大时，粒子的多样性越好；当δ_t变小时粒子的多样性会变差。因此可以设置当δ_t减小时，对下一代粒子种群进行变异。但在算法后期应当减小种群内粒子变异率，根据邢宇浩 [18] 对GSA的改进和应用研究，自适应变异触发函数可以设为：

$R_{it}={\text{e}}^{\left(-\frac{D}{2}\times \frac{t}{T}\right)}\times \left(r\times {\text{e}}^{\left(-\frac{i-1}{N}\right)}+k\right)$ (33)

其中：R_it为第t代中的第i个粒子的变异触发函数值，T为最大迭代次数，k为取值在[0.25, 0.35]之间的一个常数，一般取k = 0.3。当R_it > 0.6时，就会对当前粒子变异，r为[0, 1]内均匀分布的随机数。

对于满足变异条件的粒子采用正态分布变异，表达式为：

${\text{Normal}}_i\left(t\right)=\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{\left(\frac{{\left(x_{\text{best}}-f_{\text{fit}i}\left(t\right)\right)}^2}{2{\sigma }^2}\right)}$ (34)

其中：b_best(t)为第t次迭代时全局最优解，σ为正态分布的标准差。

4. 实例分析

4.1. 模型参数设置

以CKP6152数控机床(规格参数如表1所示，机床折旧费按200元/h计算)车削加工某型号的电机联轴器零件为例(零件材质为灰铸铁，尺寸参数如图1所示，单边加工余量为10 mm)，分析本文方法的可行性和效果。

Table 1. CKP6152 CNC lathe standard parameters

表1. CKP6152数控车床标准参数

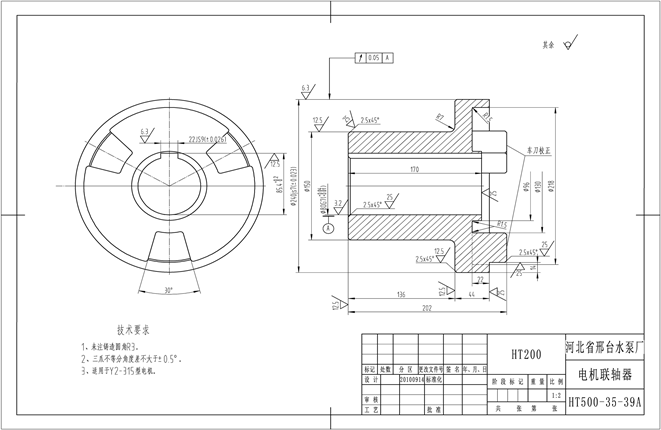
Figure 1. Dimensional drawing of three-jaw coupling parts

图1. 三爪联轴器零件尺寸图

零件未优化前单边切削加工安排为：3次粗加工和1次半精加工，前两次粗加工、最后一次粗加工和半精加工的切削深度分别为：4.0 mm、1.5 mm和0.5 mm。将切削参数带入模型可得出其碳排放量和加工成本，具体参数如表2所示。

Table 2. Original cutting parameters

表2. 原始切削加工参数

刀具材料为硬质合金车刀，刀具主偏角、前角和刀倾角分别为75˚、15˚和0˚，刀尖圆弧半径为1 mm。材料、前角和主偏角对切削力的修正系数分别为1.00、0.95和0.92，式(6)中K_Fc为前三者乘积。切削液用量和更换周期分别为13 L和28,000 min，切削力相关系数见表3，与刀具碳排放相关参数见表4。

Table 3. Correlation coefficient of cutting force calculation

表3. 切削力计算相关系数

Table 4. Correlation coefficient of cutting force calculation

表4. 刀具碳排放相关系数

4.2. 优化结果及分析

分别采用GSA算法、改进后的GSA算法对切削参数进行优化。根据经验设置粒子规模为100，迭代次数为120。实验结果如图2。

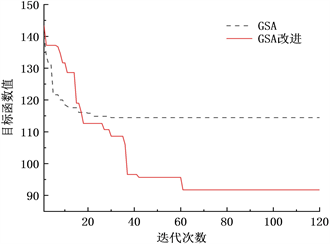
Figure 2. GSA, improved GSA algorithm

图2. GSA、改进GSA算法

分析图2，GSA算法虽然在迭代初期收敛速度比较好，但是在迭代次数为25时收敛，很快就陷入局部最优解，不再随着迭代次数增加而优化；改进后的GSA算法的收敛后的最优解与GSA算法比较有比较好的改善，由改进的GSA算法搜索到的优化结果如表。

Table 5. Final optimization result

表5. 最终优化结果

为保证零件表面粗糙度达到要求，优化过程中设置半精加工次数和刀具背吃刀量不变。对比表2和表5可知，排除其废屑等材料造成的固定碳排放，每次联轴器切削加工造成的最小碳排放为602.13 g，相比原碳排放量672.11 g而言，降低了10.41%的碳排放。采用优化后的加工参数进行车削加工，可得其成本为33.15元，相比原成本38.46元，降低了13.81%，达到了优化效果，从而证明了本文所提优化模型及改进GSA算法的有效性。

5. 结论与展望

1) 在分析了联轴器零件碳排放和加工成本的影响因素和考虑机床性能、最大切削力和表面粗糙度等约束条件的基础上，建立了基于低碳低成本的切削加工工艺参数优化模型。

2) 提出一种基于改进GSA算法的切削加工工艺参数优化求解方法。将自适应变异触发函数引入GSA，提高了算法全局搜索能力，并采用聚集度作为进行变异操作评价标准，降低了算法复杂度。

3) 通过一个具体实例，采用改进GSA对所建碳效益模型进行优化计算，得到了合理的切削参数优化结果，所建模型和方法对机械制造行业实现低碳低成本制造有一定的借鉴意义。

4) 由于数控加工类型多样，本文只是对数控加工中联轴器的切削加工工艺参数优化进行了研究，而实际制造加工过程绝大多数零件加工需要多工序、多工步完成，因此多工序、多工步的切削参数优化有待后续研究。

基金项目

浙江省2023年度“尖兵”“领雁”研发攻关计划(2022C01SA111123)，国家自然科学基金资助项目(51475434)。