基于五阶WENO格式的时间分数阶Burgers方程的多重网格方法

Multigrid Method for Time Fractional Burgers Equation Based on Fifth-Order WENO Scheme

摘要: 我们研究一种求解时间分数阶Burgers方程的多重网格方法。离散化过程中，时间分数阶导数采用L1公式逼近，对流项运用Lax-Friedrichs通量近似计算。在数值实验中，在不同的 取值下进行了有效的数值实验，结果证明该方法可以很好地模拟间断。

Abstract: We investigate a multigrid method for solving time-fractional Burgers equations. In the discretiza-tion process, the fractional derivative of time is approximated by the L1 formula, and the convective term is calculated by Lax-Friedrichs flux approximation. In the numerical experiments, the effective numerical experiments are carried out under different values of , and the results show that the method can simulate the discontinuity well.

1. 引言

本文考虑如下时间分数阶Burgers方程 [1] ：

$\frac{{\partial }^{\gamma }u\left(x,t\right)}{\partial t^{\gamma }}+2u\frac{\partial u\left(x,t\right)}{\partial x}=0$ (1)

其中 $a\le x\le b,0<t\le T$ 。

满足初始条件

$u\left(x,0\right)=g\left(x\right),a\le x\le b$

以及合适的边界条件，其中 $\gamma \in \left(0,1\right)$ ， $g\left(x\right)$ 为给定函数，

$\frac{{\partial }^{\gamma }u\left(x,t\right)}{\partial t^{\gamma }}=\frac{1}{\Gamma \left(1-\gamma \right)}{\displaystyle {\int }_0^t{\left(t-\tau \right)}^{-\gamma }\frac{\partial u\left(x,\tau \right)}{\partial \tau }\text{d}\tau }$

为 $\gamma$ 阶Caputo分数阶导数， $\Gamma \left(x\right)$ 为Gamma函数。

近十年来，许多学者运用不同的数值方法对粘性时间分数阶Burgers方程进行了求解，例如，Duangpan运用了有限积分法结合移位Chebyshev多项式 [2] ，Akram等提出了有限差分格式 [3] ，Esen和Tasbozan提出了三次b样条有限元搭配方法 [4] 等等。

2. 有限体积法离散

设 $N,M$ 是两个正整数，定义空间步长 $h=\left(b-a\right)/N$ ，空间网格节点 $x_i=a+ih$ ，其中 $i=0,1,\cdots ,N$ ；

定义空间半节点 $x_{i+\frac{1}{2}}=a+\left(i+1/2\right)h$ $\left(i=-1,0,1,\cdots ,N\right)$，得到 $N+1$ 个有限体单元 $\left[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right]$ $i=0,1,\cdots ,N$ 。

定义时间步长 $\Delta t=T/M$ ，时间网格节点 $t_k=k\Delta t$ ，其中 $k=0,1,\cdots ,M$ 。对于函数 $\mathbb{F}$ ，使用如下简写形式：

${\mathbb{F}}_{i+\frac{1}{2},n}=\mathbb{F}\left(x_{i+\frac{1}{2}},t_n\right),{\mathbb{F}}_{i+\frac{1}{2}}=\mathbb{F}\left(x_{i+\frac{1}{2}}\right).$

在 $t=t_n$ 处计算式(1)并在单元 $\left[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right]$ 上对方程进行积分，得到

$h\frac{{\partial }^{\gamma }{\bar{u}}_i\left(t_n\right)}{\partial t^{\gamma }}+\left(f{\left(u\right)}_{i+\frac{1}{2},n}-f{\left(u\right)}_{i-\frac{1}{2},n}\right)=0,i=0,1,\cdots ,N$ (2)

其中 ${\bar{u}}_i\left(t\right)={\displaystyle {\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,t\right)\text{d}x/h}$ 表示 $u\left(x,t\right)$ 在区间 $\left(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right)$ 上的平均值。

令 $U_i^n$ 表示 ${\bar{u}}_i\left(t_n\right)$ 的数值近似，对式(2)的等式左端第一项运用 $L_1$ 公式逼近 [5] ，取 $a_k={\left(k+1\right)}^{1-\alpha }-k^{1-\alpha }$ ：

$h{\frac{{\partial }^{\gamma }{\bar{u}}_i\left(t_n\right)}{\partial t^{\gamma }}|}_{t_n}\approx \frac{h\Delta t^{-\gamma }}{\Gamma \left(2-\gamma \right)}\left(U_i^n-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_{n-k-1}-a_{n-k}\right)U_i^k}-a_{n-1}{U}_i^0\right).$ (3)

其中(2)式中的通量近似为

$f{\left(u\right)}_{i+\frac{1}{2},n}\approx F\left(U_{i+\frac{1}{2}}^{n,-},U_{i+\frac{1}{2}}^{n,+}\right)$ (4)

$f{\left(u\right)}_{i-\frac{1}{2},n}\approx F\left(U_{i-\frac{1}{2}}^{n,-},U_{i-\frac{1}{2}}^{n,+}\right)$ (5)

结合式(2)、(3)、(4)及(5)，可以得到最终的离散形式为

$\frac{h\Delta t^{-\gamma }}{\Gamma \left(2-\gamma \right)}\left(U_i^n-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_{n-k-1}-a_{n-k}\right)U_i^k}-a_{n-1}{U}_i^0\right)+F\left(U_{i+\frac{1}{2}}^{n,-},U_{i+\frac{1}{2}}^{n,+}\right)-F\left(U_{i-\frac{1}{2}}^{n,-},U_{i-\frac{1}{2}}^{n,+}\right)=0.$ (6)

(6)式中的 $F\left(U_{i+\frac{1}{2}}^{n,-},U_{i+\frac{1}{2}}^{n,+}\right)$ 是Lax-Friedrichs通量，即

$F\left(U_{i+\frac{1}{2}}^{n,-},U_{i+\frac{1}{2}}^{n,+}\right)=\frac{f\left(U_{i+\frac{1}{2}}^{n,-}\right)+f\left(U_{i+\frac{1}{2}}^{n,+}\right)}{2}-\frac{\gamma }{2}\left(U_{i+\frac{1}{2}}^{n,+}-U_{i+\frac{1}{2}}^{n,-}\right).$ (7)

其中，取 $\gamma$ 为 $\gamma =\kappa \underset{w}{\max }\left|f^{\prime }\left(w\right)\right|$ ， $U_{i+\frac{1}{2}}^{n,-}$ ， $U_{i+\frac{1}{2}}^{n,+}$ 分别表示在节点 $x_{i+1/2}$ 上的左近似与右近似，对于左近似和右近似，在下一节中将详细阐述。

3. 5阶WENO格式

对于上一节中的左近似与右近似： $U_{i+\frac{1}{2}}^{n,-}$ ， $U_{i+\frac{1}{2}}^{n,+}$ ，我们用5阶WENO格式重构近似计算，该算法是将 $U_{i+\frac{1}{2}}^{n,-}$ 和 $U_{i+\frac{1}{2}}^{n,+}$ 分别利用一系列偏左、右侧的点值重构得到的。经典的五阶WENO格式如图1所示。

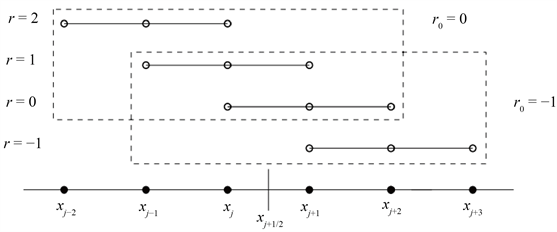
Figure 1. The model of the fifth-order WENO scheme

图1. 5阶WENO示意图

$U_{i+\frac{1}{2}}^{n,-}$ 是利用图1一系列偏左侧的点重构得到的(即图1中的 $r_0=0$ )， $U_{i+\frac{1}{2}}^{n,+}$ 是利用图1一系列偏右侧的点重构得到的(即图1中的 $r_0=-1$ )，这里 $r_0$ 表示r的初始点。为了简化描述，在不引起混淆的情况下，省去 $U_{i+\frac{1}{2}}^{n,-}$ 和 $U_{i+\frac{1}{2}}^{n,+}$ 的上标“+”，“−”和“n”。 $U_{i+\frac{1}{2}}$ 的五阶WENO重构可表示为：

$U_{i+\frac{1}{2}}={\displaystyle \underset{r=r_0}{\overset{2+r_0}{\sum }}{\omega }_r^{r_0}{U}_{i+\frac{1}{2}}^{\left(r\right)}}$ (8)

(8)式中的 $U_{i+\frac{1}{2}}^{\left(r\right)}$ 可写为 $U_{i+\frac{1}{2}}^{\left(r\right)}={\displaystyle \underset{j=0}{\overset{2}{\sum }}{c}_{jr}^3{\bar{U}}_{i-r+j}}$ ，非线性权重 ${\omega }_r^{r_0}$ 为

${\omega }_r^{r_0}=\frac{{\sigma }_r}{{\displaystyle {\sum }_{s=0}^2{\sigma }_s}},{\sigma }_r=\frac{d_r^{r_0}}{{\left(\epsilon +{\beta }_r\right)}^2}$ (9)

其中， $\epsilon \ll 1$ ，通常取 $\epsilon ={10}^{-6}$ ， $d_r^{r_0}$ 是线性权重。上述中系数 $c_{jr}^3$ 和 $d_r^{r_0}$ 的选取可参见文献 [6] 。

光滑指示因子 ${\beta }_r$ 可以表示为：

$\{\begin{array}{l}{\beta }_0=\frac{13}{12}{\left({\bar{U}}_i-2{\bar{U}}_{i+1}+{\bar{U}}_{i+2}\right)}^2+\frac{1}{4}{\left(3{\bar{U}}_i-4{\bar{U}}_{i+1}+{\bar{U}}_{i+2}\right)}^2,\\ {\beta }_1=\frac{13}{12}{\left({\bar{U}}_{i-1}-2{\bar{U}}_i+{\bar{U}}_{i+2}\right)}^2+\frac{1}{4}{\left({\bar{U}}_{i-1}-{\bar{U}}_{i+1}\right)}^2,\\ {\beta }_2=\frac{13}{12}{\left({\bar{U}}_{i-2}-2{\bar{U}}_{i-1}+{\bar{U}}_i\right)}^2+\frac{1}{4}{\left({\bar{U}}_{i-2}-4{\bar{U}}_{i-1}+3{\bar{U}}_i\right)}^2.\end{array}$

4. 多重网格方法

本文使用多重网格迭代方法，由于空间系统是强非线性的，我们将使用非线性多重网格方法——FAS多重网格方法 [7] 。

假设三个正整数 $N,N_0,level$ 满足式：

$N=N_0\times 2^{level-1}$

构建一个空间网格体系 ${\left\{{\Gamma }_k\right\}}_{k=1}^{level}$ ，假设最细网格 ${\Gamma }_1$ 的网格大小为 $h_1=h$ ，对于 $k=2,3,\cdots ,level$ ， ${\Gamma }_k$ 的网格大小为 $h_k=2^{k-1}h$ ，其中 $N_k=N/2^{k-1}$ 表示 ${\Gamma }_k$ 的网格数量，下文中与 ${\Gamma }_k$ 有关的量以上标 $h_k$ 的形式书写，例如 $U^{h_k}$ 。

在每一层网格上，对问题采用如下不动点迭代方法求解：

$\left(\frac{h_k\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}+{\lambda }^{h_k}{h}_k\right){\hat{V}}_i^{h_k}=r_i^{h_k}+{\lambda }^{h_k}{h}_k{\tilde{V}}_i^{h_k}-\left(F\left({\tilde{V}}_{i+\frac{1}{2}}^{h_k,-},{\tilde{V}}_{i+\frac{1}{2}}^{h_k,+}\right)-F\left({\tilde{V}}_{i-\frac{1}{2}}^{h_k,-},{\tilde{V}}_{i-\frac{1}{2}}^{h_k,+}\right)\right),$ (10)

其中 $r_i^{h_k}=\frac{h_k\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left({\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_{n-k-1}-a_{n-k}\right){\tilde{V}}_i^k}+a_{n-1}{\tilde{V}}_i^0\right)$ ， ${\hat{V}}^{h_k}$ 和 ${\tilde{V}}^{h_k}$ 分别为一次迭代过程中的新近似解和旧近似

解， ${\lambda }^{h_k}$ 为一个能够保证迭代方法收敛性的合适的正数。

下面提出求解方程的两层多重网格迭代方法，我们定义延拓和限制算子来实现相邻网格之间的数据传输，其中，延拓算子定义为 $I_{2h}^h$ ，即

$U^h=I_{2h}^h{U}^{2h}$

定义为：

$\{\begin{array}{l}{U}_{2i}^h=U_i^{2h}\\ U_{2i+1}^h=\frac{1}{2}\left(U_i^{2h}+U_{i+1}^{2h}\right)\end{array}$

限制算子定义为 $I_h^{2h}$ ，即

$U^{2h}=I_h^{2h}{U}^h$

定义为：

$U_i^{2h}=\frac{1}{4}\left(U_{2i-1}^h+2U_{2i}^h+U_{2i+1}^h\right)$

以下提出求解方程的多重网格迭代方法步骤：

步1：在细网格上运用(8)式计算离散方程 $A\left(u^h\right)=f^h$ ，一般迭代次数为2~3次；

步2：细网格上的残差和近似解均限制到粗网格上，并求解细网格上离散方程:

$A^{2h}\left(u^{2h}\right)=A^{2h}\left(I_h^{2h}{\bar{u}}^h\right)+I_h^{2h}\left(f^h-A^h\left({\bar{u}}^h\right)\right)=f^{2h}$

步3：作粗网格修正：

${\overline{\stackrel{¯}{u}}}^h\leftarrow {\bar{u}}^h+I_{2h}^h\left({\overline{\stackrel{¯}{u}}}^{2h}-{\bar{u}}^{2h}\right).$

5. 数值实验

算例1令计算域为 $\left[a,b\right]\times \left(0,T\right]=\left[-1,3\right]\times \left(0,0.2\right]$ ，初始条件为 $u\left(x,0\right)=-\sin \left(\pi x\right)$ ，边值条件为 $u\left(a\right)=u\left(b\right)=0$ ，取 $N=256$ ， $M=100$ ，当 $\gamma =0.9,0.7,0.5,0.3$ 时方程(1)的数值解如下图2：

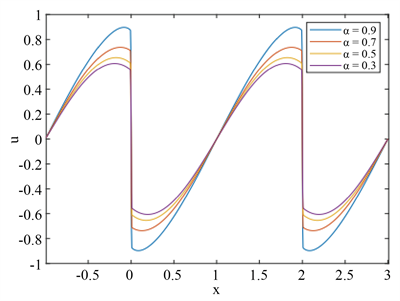
Figure 2. Numerical results of example 1

图2. 算例1的数值结果

算例2令计算域为 $\left[a,b\right]\times \left(0,T\right]=\left[-1,2\right]\times \left(0,0.2\right]$ ，初始条件为 $u\left(x,0\right)=\{\begin{array}{l}0,x\ge 0\\ 1,x<0\end{array}$ ，边值条件为

$u\left(a\right)=1,u\left(b\right)=0$ ，取 $N=256,M=128$ ，当 $\gamma =0.9,0.7,0.5,0.3$ 时方程(1)的数值解如下图3：

根据图2和图3，我们可以看出：算例1中的初始条件是连续函数，随着时间的推进，数值解演化成激波；算例2中的初始条件是分段函数，然而随着时间的推进，数值解演化成稀疏波。

Figure 3. Numerical results of example 2

图3. 算例2的数值结果

6. 总结

本文运用多重网格迭代方法求解时间分数阶Burgers方程，对于对流项中的通量，我们运用Lax-Friedrichs通量近似计算，并对于通量中的左近似和右近似采用5阶WENO格式重构近似。文中计算了两个算例在 $\gamma =0.9,0.7,0.5,0.3$ 时方程的数值解，可以看出该方法模拟间断的效果很好。

NOTES

^*通讯作者。