基于退化量分布的电连接器绝缘可靠性建模

Insulation Reliability Modeling of Electrical Connectors Based on Degradation Distribution

摘要: 针对贮存环境下电连接器的绝缘可靠性评估问题，通过对聚氨酯胶绝缘件在贮存条件下的失效机理分析，揭示了电连接器发生绝缘失效是由于聚氨酯胶发生了氧化和水解。基于表面中心复合法(CCF)设计并开展九组双应力加速试验，获取绝缘件在不同应力组合下各个检测时刻的退化量。基于Anderson-Darling统计对退化量进行最优分布拟合，确定聚氨酯胶绝缘件的绝缘电阻最优服从正态分布，并建立了聚氨酯胶绝缘件的退化量分布模型。通过比较拟合优度，确定了退化量分布模型中均值和标准差的时间函数形式为指数函数，并利用最小二乘法对模型未知参数进行估计。基于响应曲面理论，建立了参数的温湿度双应力加速模型。基于系统可靠性的串联关系，建立了电连接器的绝缘可靠性模型，计算了电连接器绝缘件在正常应力下的可靠寿命，可以为贮存环境下电连接器的绝缘可靠性评估提供参考。

Abstract: Aiming at the evaluation of insulation reliability of electrical connectors in storage environment, the failure mechanism of polyurethane adhesive insulation parts under storage conditions is analyzed, and it is revealed that the insulation failure of electrical connectors is due to oxidation and hydroly-sis of polyurethane adhesive. Based on the surface center composite method (CCF), nine sets of dou-ble stress accelerated tests were designed and carried out to obtain the degradation of insulation at each detection time under different stress combinations. Based on Anderson-Darling statistics, the optimal distribution of degradation is fitted, and the optimal insulation resistance of polyurethane rubber insulation is determined to follow the normal distribution, and the degradation distribution model of polyurethane rubber insulation is established. By comparing the goodness of fit, the time function form of the mean and standard deviation in the degradation quantity distribution model is determined as exponential function, and the unknown parameters of the model are estimated by the least square method. Based on the response surface theory, a parametric temperature and hu-midity dual stress acceleration model is established. Based on the series relationship of system re-liability, the insulation reliability model of electrical connector is established, and the reliable life of electrical connector insulation under normal stress is calculated, which can provide reference for the insulation reliability evaluation of electrical connector in storage environment.

1. 引言

对于“长期贮存、一次使用”的武器装备，服役后主要处于贮存状态。电连接器是各类武器装备系统中用于传递能量和信号的一种基础元件，应用数量大，只要有一个电连接器发生失效，就有可能导致整个系统发生失效，是武器装备性能和战斗力保持的关键瓶颈 [1] [2] 。

电连接器通常由接触件、绝缘件和壳体等组成。绝缘件用于电连接器插针之间的安装和定位，使插针按照设计要求进行有序排列；电连接器插针之间的孔距通常只有几毫米左右，绝缘件通过自身优良的绝缘性能，保证了电连接器插针之间以及插针与壳体之间的绝缘可靠性。长期处于贮存环境下的电连接器，其绝缘件在环境应力作用下性能会发生退化，具体表现形式为绝缘电阻的降低，形成漏电流影响电连接器电信号的传输 [3] ，甚至是插针之间发生短路，因此有必要对电连接器绝缘件的贮存可靠性进行研究。

目前关于电连接器的可靠性研究大多围绕接触件，关于绝缘件的研究较少。例如，许彬彬等 [4] 通过对瓷管电容滤波电连接器的进行失效分析，结果表明瓷管电容表面存在污染物导致电连接器发生失效。马杰 [5] 通过测试不同温度下电连接器的绝缘电阻，分析出温度对电连接器绝缘性能的影响规律。薛云智 [6] 等阐述并通过试验验证了温度和湿度是影响电连接器绝缘电阻的主要因素。高亮等 [7] 通过对试验数据进行统计分析，揭示了电连接器的绝缘电阻随温度和真空度的变化规律。崔洁等 [8] 通过测试常态和高湿环境下的绝缘电阻，研究了焊接工艺和清洗过程对电连接器绝缘可靠性的影响。这些研究通过理论分析和试验验证找到了影响电连接器绝缘可靠性的因素，但不能预测贮存环境下电连接器的绝缘性能随时间的演变规律和贮存可靠性。

本文以电连接器用聚氨酯胶绝缘件为对象，针对贮存环境下温湿度对电连接器绝缘可靠性的影响和绝缘件的贮存寿命评估问题，通过开展绝缘件的双应力加速试验，从数据统计角度出发分别建立了退化量分布模型和双应力加速模型并对模型参数进行估计，最终建立了电连接器的绝缘可靠性模型，计算了电连接器绝缘件在贮存环境下的可靠寿命，为电连接器的绝缘可靠性评估提供了数据基础。

2. 失效分析

聚氨酯胶作为电连接器的常用绝缘材料之一，在长期贮存环境下，造成贮存环境下电连接器聚氨酯胶绝缘材料绝缘失效的原因主要有：

1) 温度的影响

温度使聚氨酯胶绝缘材料内的高分子运动加剧发生热氧反应 [9] ，一旦能量超过原子间化学键的键能，聚氨酯胶的高分子链断裂，生成许多游离态的离子基团，载流子浓度增加，材料的电导率增加，降低了聚氨酯胶绝缘材料的绝缘性能。

2) 湿度的影响

空气中的湿气会进入聚氨酯胶内部，使其电气性能降低，直至被完全破坏。水对聚氨酯胶有增塑作用 [10] ，即水分子渗透到大分子链中，削弱聚合物主链分子间氢键的作用，使聚合物的拉伸强度、撕裂强度和耐磨性明显下降，通过破坏其机械性能使材料变得脆弱而无法完成绝缘。

3) 温度和湿度的影响

在聚氨酯胶绝缘件的老化过程中，温度和湿度存在相互促进作用，温度和湿度的综合影响体现在以下两个方面：一是温度可以改变贮存环境的水蒸汽压，温度越高，水分渗透进入聚氨酯胶内部的能力增加，加速了聚氨酯胶绝缘件的受潮。二是温度可以使聚氨酯胶分子链的热运动加剧，分子间的作用力降低，分子间孔隙增大，加快了水分子进入聚氨酯胶的速率，同样加快了聚氨酯胶绝缘件的受潮。

综上所述，电连接器绝缘性能退化的原因是聚氨酯胶发生了氧化和水解，温度和湿度是电连接器发生绝缘失效的主要影响因素。

3. 试验方案设计

因电连接器用聚氨酯胶绝缘件的最高耐受温度为85℃，在不改变聚氨酯胶失效机理的前提下，对其进行温湿度双应力加速试验。试验的最高温度设定为75℃，最低温度设定为55℃；在试验设备可行的范围内，将最大试验湿度设定为96%RH，最低试验湿度为72%RH。考虑到试验数据的统计要求，每组试验样品取5个。每个绝缘件样品上有10根插针，试验过程中定时检测聚氨酯胶绝缘件相邻两根插针之间的绝缘电阻值，每个样品有19个绝缘电阻数据。任意相邻两根插针之间的绝缘电阻小于1 GΩ，可认为绝缘件发生绝缘失效。

为了分析温度和湿度对聚氨酯胶绝缘性能的线性效应、非线性效应以及交互效应，根据响应曲面设计中的表面中心复合法(CCF)进行试验方案设计，具体试验方案如表1所示。

4. 退化量分布建模

4.1. 最优分布族的确定

从每组试验中任意抽取1个试验样品，对其试验数据进行可视化呈现，每个绝缘件样品的绝缘电阻退化轨迹如图1所示。

Table 1. Test plan

表1. 试验方案

(1) 55℃、72%RH组样品1 (2) 55℃、84%RH组样品3 (3) 55℃、96%RH组样品4 (4) 65℃、72%RH组样品1 (5) 65℃、84%RH组样品4 (6) 65℃、96%RH组样品5 (7) 75℃、72%RH组样品2 (8) 75℃、84%RH组样品3 (9) 75℃、96%RH组样品5

Figure 1. Insulation resistance degradation track of nine groups of tests

图1. 九组试验的绝缘电阻退化轨迹

图例中，“1-2”表示绝缘件上插针1和插针2之间的绝缘电阻值。从图3可以看出，九组试验的绝缘电阻值在退化过程中虽有波动现象，但整体退化趋势明显，绝缘电阻呈下降趋势。

Anderson-Darling检验是分析最优分布拟合的常用方法，本文采用A-D检验对九个应力水平下绝缘件在各个退化时刻的绝缘电阻值进行最优分布拟合分析，以65℃、84%RH组为例，在第1176 h试验时刻退化量的最优拟合分布结果如图2所示。

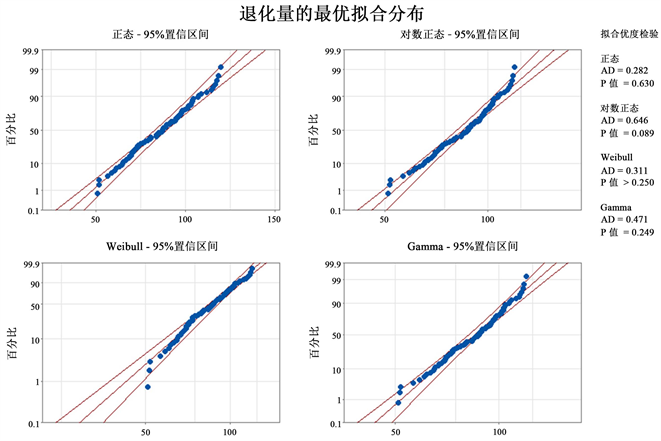
Figure 2. Optimal fitting distribution of degradation at 1176th h in 65˚C and 84% RH group

图2. 65℃、84%RH组第1176 h退化量的最优拟合分布

Anderson-Darling检验结果中，P值表示AD统计量与临界值的比较结果，若P值大于显著性水平0.05，则表示在95%置信度下认为退化量服从该分布，AD值越小，表明退化量与指定分布的拟合程度越高；从图中可以看出，正态分布的AD值越小，表明65℃、84%RH组在第1176 h试验时刻退化量的最优服从正态分布。九组试验在各个检测时刻绝缘电阻的最优拟合分布结果统计如表2所示。

Table 2. Statistics of best fit distribution results

表2. 最优拟合分布结果统计

根据表2，9个应力水平下一共有96组退化量，其中71组最优服从正态分布，12组最优服从对数正态分布，12组最优服从威布尔分布；由于绝大多数退化时刻的退化量最优服从正态分布 [11] ，且剩余的24组退化量最优服从对数正态分布或者威布尔分布但又同时服从正态分布，可认为绝缘件样品的绝缘电阻值最优服从正态分布。

4.2. 退化量分布模型

聚氨酯胶绝缘件的绝缘电阻服从正态分布 $r_{ijk}~\left({\mu }_{jk},{\sigma }_{jk}^2\right)$ ，其中， $r_{ijk}$ ( $i=1,2,\cdots ,n$ ； $j=1,2,\cdots ,l$ ； $k=1,2,\cdots ,q$ )表示第i个绝缘件样品在第k个应力水平下第j次测量的退化量(绝缘电阻值)， $t_{jk}$ 为样品退化量的对应测量时间点。 ${\mu }_{jk}$ 为均值， ${\sigma }_{jk}$ 为标准差，可通过式(1)计算

${\hat{\mu }}_{jk}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{r}_{ijk}},{\hat{\sigma }}_{jk}{}^2=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(r_{ijk}-{\hat{\mu }}_{jk}\right)}^2}$ (1)

对于绝缘件的绝缘性能，当绝缘电阻 $r_{ijk}$ 小于失效阈值D时，认为绝缘件发生绝缘失效，则绝缘件样品的失效分布函数为

$F\left(t\right)=P\left(r_{ijk}\le D\right)$ (2)

绝缘电阻 $r_{ijk}$ 服从正态分布，产品的失效分布函数为

$F\left(t\right)=P\left(r_{ijk}\le D\right)={\displaystyle {\int }_0^D\frac{1}{\sqrt{2\pi }{\sigma }_{jk}\left(t\right)}}\exp \left(-\frac{{(r-{\mu }_{jk}\left(t\right))}^2}{2{\sigma }^2{}_{jk}\left(t\right)}\right)\text{d}r$ (3)

可靠度 $R(t)$ 为

$\begin{array}{c}R\left(t\right)=1-F\left(t\right)=1-{\displaystyle {\int }_0^D\frac{1}{\sqrt{2\pi }{\sigma }_{jk}\left(t\right)}}\exp \left(-\frac{{\left(r-{\mu }_{jk}\left(t\right)\right)}^2}{2{\sigma }^2{}_{jk}\left(t\right)}\right)\text{d}r\\ =1-\Phi \left(\frac{D-{\mu }_{jk}\left(t\right)}{{\sigma }_{jk}\left(t\right)}\right)\\ =\Phi \left(\frac{{\mu }_{jk}\left(t\right)-D}{{\sigma }_{jk}\left(t\right)}\right)\end{array}$ (4)

式中， $\Phi$ 为标准正态分布概率， ${\mu }_{jk}\left(t\right)$ 为均值的时间函数，即常见的退化轨迹模型拟合各个时刻的 ${\mu }_{jk}$ 得到的最优均值函数； ${\sigma }_{jk}\left(t\right)$ 为标准差的时间函数，即常见的退化轨迹模型拟合拟合各个时刻的 ${\sigma }_{jk}$ 得到的最优标准差函数。

4.3. 模型参数估计

常见的退化轨迹模型有：

线性模型：

$m\left(t\right)=-at+b$ (5)

幂函数模型：

$m\left(t\right)=a{t}^{-b}$ (6)

指数函数模型：

$m\left(t\right)=a{\text{e}}^{-bt}$ (7)

其中， $m\left(t\right)$ 为 $m$ 的时间函数； $a、b$ 为待估参数。

将3种常见的退化轨迹模型对 ${\mu }_{jk}\left(t\right)$ 、 ${\sigma }_{jk}\left(t\right)$ 进行拟合，选择拟合优度最高的一种作为退化轨迹模型。可采用 $R^2$ 评价函数模型的拟合优度， $R^2$ 的计算公式为

$\begin{array}{l}{R}^2=\frac{SSE}{SST}=\frac{SSE}{SSE+SSR}\\ SSE={\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{\left(y_i-{\hat{y}}_i\right)}^2}\\ SSR={\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{\left({\hat{y}}_i-\bar{y}\right)}^2}\end{array}$ (8)

式中，其中， $y_i$ 为观测值； ${\hat{y}}_i$ 为预测值； $\bar{y}$ 为观测值均值。

九组试验均值的时间函数与标准差的时间函数的拟合优度 $R^2$ 分别如表3和表4所示。

Table 3. Goodness-of-fit result of mean time function

表3. 均值时间函数的拟合优度结果

Table 4. Goodness-of-fit result of standard deviation time function

表4. 标准差时间函数的拟合优度结果

$R^2$ 的取值范围是(0, 1)， $R^2$ 越接近1，则模型的拟合程度越高，通过比较九组应力水平下均值时间函数和标准差时间函数的拟合优度 $R^2$ ，确定均值时间函数和标准差时间函数的最优拟合函数模型均为指数函数，可表示为

${\hat{\mu }}_{jk}=a_k{\text{e}}^{-b_k{t}_k},{\hat{\sigma }}_{jk}=c_k{\text{e}}^{-d_k{t}_k}$ (9)

式中， $a_k$ 、 $b_k$ 、 $c_k$ 、 $d_k$ 为待估参数。

计算各个应力下所有插针与插针之间绝缘电阻在各个退化时刻的均值和标准差，利用最小二乘法对九组试验所有插针之间绝缘电阻均值的时间函数模型和标准差的时间函数模型中的待估参数进行估计，结果如表5所示。

Table 5. Parameter estimation results

表5. 参数估计结果

5. 可靠性评估

5.1. 失效机理一致性检验

根据加速因子不变原则 [12] 推导参数与加速应力的关系。加速寿命试验中对加速因子定义 [12] 为：产品承受的加速应力为S，第k级和第h级加速应力分布表示为 $S_k$ 和 $S_h$ ，在可靠度为R时，产品的可靠寿命分别为 $t_{R,k}$ 和 $t_{R,h}$ ，时间比 $A{F}_{k,h}=t_{R,h}/t_{R,k}$ ，即为 $S_k$ 对 $S_h$ 的加速因子。则 $F_k\left(t_k\right)=F_h\left(t_h\right)$ ，对于任意的 $t_k$ 恒成立，将式(9)代入式(4)可得到绝缘件上插针与插针之间的退化量分布模型

$R\left(t\right)=1-F\left(t\right)=\Phi \left(\frac{a_k{\text{e}}^{-b_k{t}_k}-D}{c_k{\text{e}}^{-d_k{t}_k}}\right)$ (10)

由于 $F_k\left(t_k\right)=F_h\left(t_h\right)$ ，则式(10)可表示为

$\Phi \left(\frac{D-a_k{\text{e}}^{-b_k{t}_k}}{c_k{\text{e}}^{-d_k{t}_k}}\right)=\Phi \left(\frac{D-a_h{\text{e}}^{-b_h{t}_h}}{c_h{\text{e}}^{-d_h{t}_h}}\right)$ (11)

保证任意 $t_k$ 对式(11)成立，则

$D-a_k{\text{e}}^{-b_k{t}_k}=D-a_h{\text{e}}^{-b_h{t}_h},c_k{\text{e}}^{-d_k{t}_k}=c_h{\text{e}}^{-d_h{t}_h}$ (12)

把 $A{F}_{k,h}=t_{R,h}/t_{R,k}$ 代入式(12)可推出

$\{\begin{array}{l}{a}_k=a_h,A{F}_{k,h}=b_k/b_h\\ c_k=c_h,A{F}_{k,h}=d_k/d_h\end{array}$ (13)

由式(13)可知 $a_k$ 和 $c_k$ 在各个应力下保持不变， $b_k$ 和 $d_k$ 随着应力的改变而改变。

为了验证失效机理是否发生改变，分别将 ${\hat{a}}_k=\left({\hat{a}}_1,{\hat{a}}_2,\cdots ,{\hat{a}}_5\right)$ 、 ${\hat{c}}_k=\left({\hat{c}}_1,{\hat{c}}_2,\cdots ,{\hat{c}}_5\right)$ (k为应力序号)作为检验样本，检验各个应力下的 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 是否存在显著差异。采用t-test检验法对其进行检验，具体检验步骤如下：

1) 利用A-D统计量对 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 分别进行正态分布的假设检验，在显著性水平为0.05时接受 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 在九个加速应力下服从正态分布的假设。检验样本 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 与的正态分布拟合结果如图3所示。

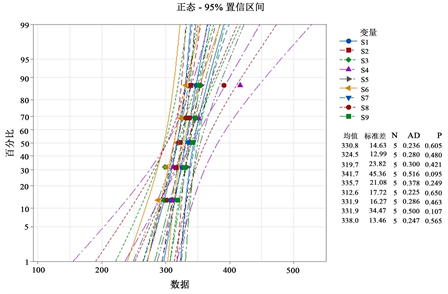
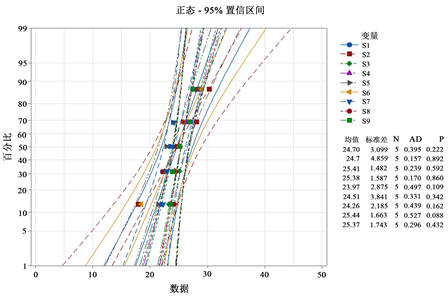
(a) 样本 ${\hat{a}}_k$ 的正态分布拟合结果 (b) 样本 ${\hat{c}}_k$ 的正态分布拟合结果

Figure 3. Normal fitting results of parameters

图3. ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 的正态分布拟合结果

2) 设 $X_1,X_2,\cdots ,X_n$ 是来自 $N\left({\mu }_1,{\sigma }^2\right)$ 的样本， $Y_1,Y_2,\cdots ,Y_n$ 是来自 $N\left({\mu }_2,{\sigma }^2\right)$ 的样本，原假设 $H_0:{\mu }_1={\mu }_2$ ，备选假设 ${\mu }_1\ne {\mu }_2$ ，建立如下t统计量：

$t=\sqrt{\frac{nm}{n+m}}\frac{\bar{X}-\bar{Y}}{S_w}$ (14)

式中，

$\begin{array}{l}\bar{X}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{X}_i,}\bar{Y}=\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{Y}_i}\\ S_w^2=\frac{\left(n-1\right)S_1^2+\left(m-1\right)S_2^2}{n+m-2}\\ S_1^2=\frac{1}{n-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(X_i-\bar{X}\right)}^2}\\ S_2^2=\frac{1}{m-1}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\left(Y_i-\bar{Y}\right)}^2}\end{array}$ (15)

由于，

$\sqrt{\frac{nm}{n+m}}\frac{\bar{X}-\bar{Y}}{S_w}~t\left(n+m-2\right)$ (16)

当显著水平为 $\alpha$ 时，原假设的拒绝域为

$\sqrt{\frac{nm}{n+m}}\frac{\bar{X}-\bar{Y}}{S_w}\ge t_{1-\alpha /2(n+m-2)}$ (17)

3) 逐一对九个应力中任意两个应力的 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 进行检验，当显著水平为0.05时，得拒绝域的下边界为 $t_{0.975}\left(8\right)=2.306$ 。检验的部分结果如表6所示，t统计量均小于2.306且P值均大于0.05，九个应力下的检验样本 ${\hat{a}}_k$ 和 ${\hat{c}}_k$ 没有显著性差异，绝缘件在九个应力下的失效机理具有一致性。

Table 6. Failure mechanism consistency check

表6. 失效机理一致性检验

5.2. 参数的加速模型

参数 $b_k$ 和 $d_k$ 与绝缘件所受的应力有关，参数的响应曲面方程 [13] 为

$\ln y={\beta }_0+{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\beta }_i{x}_i+}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\beta }_{ii}{x}_i{}^2+}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\beta }_{ij}{x}_i{x}_j+}\epsilon$ (18)

其中，y为参数 $b_k$ 、 $d_k$ ；m为影响因子个数(本文取m = 2； $x_i$ 是影响因子( $x_i$ 为温度因子， $x_j$ 为湿度因子)； ${\beta }_i$ ， ${\beta }_{ii}$ ， ${\beta }_{ij}$ 为多项式的回归系数(i < j)， ${\beta }_i$ 表示 $x_i$ 的线性效应， ${\beta }_{ii}$ 表示 $x_i$ 的二次效应， ${\beta }_{ij}$ 表示 $x_i$ 与 $x_j$ 之间的交互效应；ε为误差项。

根据式(18)分别对 $b_k$ 、 $d_k$ 建立双应力加速模型如式(19)所示

$\begin{array}{l}\ln b_k=-18.537+0.25633x_1+0.05083x_1-1.867\times {10}^{-3}{x}_1{}^2-3.24\times {10}^{-4}{x}_2{}^2+1.67\times {10}^{-4}{x}_1{x}_2\\ \ln d_k=-6.163+0.32992x_1-0.36247x_1-2.2\times {10}^{-3}{x}_1{}^2+2.187\times {10}^{-3}{x}_2{}^2+1.04\times {10}^{-4}{x}_1{x}_2\end{array}$ (19)

5.3. 贮存寿命

绝缘件上插针与插针之间的退化量分布模型为

$R\left(t\right)=\Phi \left(\frac{a_k{\text{e}}^{-b_{k}t}-D}{c_k{\text{e}}^{-d_{k}t}}\right)$ (20)

一个绝缘件上有10根针，19个绝缘电阻测量点。其可靠度是由最先出现绝缘失效的相邻的两根针之间的绝缘电阻决定的，则绝缘件的寿命可表现为：

$T=\min \left\{T_1,T_2,T_3,\cdots ,T_{19}\right\}$

按照系统可靠性中的串联关系来建立绝缘件的寿命分布，则绝缘件的可靠度模型为

$R_1\left(t\right)=R{\left(t\right)}^{19}={\left[\Phi \left(\frac{a_k{\text{e}}^{-b_{k}t}-D}{c_k{\text{e}}^{-d_{k}t}}\right)\right]}^{19}$ (21)

式中， $a_k$ 、 $b_k$ 、 $c_k$ 和 $d_k$ 为应力k下样品的待估参数， $D$ 为绝缘件的失效阈值， $\Phi$ 为标准正态分布概率，t为绝缘件的退化时间。

$a_k$ 和 $c_k$ 与绝缘件的应力无关，因此正常贮存环境(25℃, 50%RH)下

$\begin{array}{l}{a}_0=\frac{1}{9}{\displaystyle \underset{i=1}{\overset{9}{\sum }}{a}_i}=330.82\\ b_0=\frac{1}{9}{\displaystyle \underset{i=1}{\overset{9}{\sum }}{b}_i}=25.19\end{array}$ (22)

$b_k$ 、 $d_k$ 与绝缘件应力有关，把 $x_1=25℃、x_2=50\%RH$ 代入式(19)，可得正常贮存环境下的参数

$\begin{array}{l}{b}_0=1.1703\times {10}^{-5}\\ d_0=7.3980\times {10}^{-6}\end{array}$ (23)

电连接器绝缘件在贮存环境(25℃, 50%RH)下的可靠度模型为

$R_1\left(t\right)={\left[\Phi \left(\frac{330.82{\text{e}}^{-1.1703\times {10}^{-5}t}-1}{25.19{\text{e}}^{{}^{-7.3980\times {10}^{-6}t}}}\right)\right]}^{19}$ (24)

电连接器绝缘件在贮存环境(25℃, 50%RH)下的可靠度曲线如图4所示。

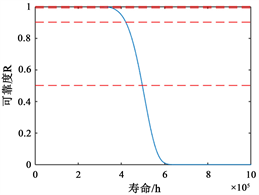
Figure 4. Reliability curve of electrical connector insulation

图4. 电连接器绝缘件可靠度曲线

电连接器绝缘件在贮存环境(25℃, 50%RH)下的可靠寿命如表7所示。考虑到这类绝缘件在实际工程应用中的寿命一般在30~40年之间不等 [14] ，可以认为本文所提出的基于退化量分布的电连接器绝缘可靠性模型给出的评估结果较为准确。

Table 7. Reliable life of polyurethane rubber insulating parts for electrical connectors under storage environment (25˚C, 50% RH)

表7. 贮存环境(25℃, 50%RH)下电连接器用聚氨酯胶绝缘件的可靠寿命

注： $t_{0.999}$ 表示为可靠度为0.999时的贮存寿命。

6. 结论

本文提出的基于退化量分布的可靠性模型可以为贮存环境下电连接器的绝缘可靠性评估和寿命预测提供指导。本文以电连接器用聚氨酯胶绝缘件为对象，介绍了电连接器绝缘件贮存寿命评估的关键步骤，包含失效机理分析、加速试验设计、退化量分布建模、双应力加速模型的建立、参数估计和贮存可靠性评估，结论如下：

1) 本文针对电连接器常用的聚氨酯胶绝缘材料，其失效机理为聚氨酯胶的氧化和水解，温度和湿度是电连接器发生绝缘失效的主要的环境影响因素。

2) 根据响应曲面理论设计的双应力加速试验的应力组合具有均匀性和代表性。A~D统计量拟合优度检验结果显示，绝缘件退化量的最优拟合分布为正态分布，绝缘电阻数据在退化过程中存在波动，用退化量分布模型可以很好地描述绝缘件的退化过程。

3) t-test统计量检验结果表明九个应力组合下绝缘件样品的失效机理具有一致性，验证了加速试验方案的合理性和试验数据的有效性。

4) 每个电连接器绝缘件上有多个绝缘电阻测量点，任意一个测量点发生失效都会导致整个绝缘件的失效，因此可根据串联系统可靠性模型评估整个绝缘件的贮存可靠性。

基金项目

浙江省重点研发项目(2021C01133)。