一种基于回溯求解约束满足问题的置信传播算法

A Belief Propagation Algorithm for Constraint Satisfaction Problem Based on Backtracking

摘要: 针对一个典型的具有可变取值域的随机约束满足问题模型即RB模型，提出一种基于回溯的置信传播的算法。该算法在置信传播方程不收敛时，通过回溯对上一个变量进行重新赋值，从而将消去变量的过程继续进行下去。数值结果表明：这种基于回溯的置信传播算法能在可满足性相变区域找到问题的解，有效地提高了置信传播算法的求解效率。

Abstract: In this paper, we propose a belief propagation algorithm based on backtracking for a typical model of random constraint satisfaction problem with variable range, namely RB model. In this algorithm, when the belief propagation equation does not converge, it reassigns the previous variable by backtracking, so as to continue the process of variable elimination. The numerical results show that the backtracking belief propagation algorithm can find the solution of the problem in the satisfia-bility phase transition region, and effectively improve the efficiency of the belief propagation algo-rithm.

1. 引言

消息传递算法的迭代特性捕获了复杂系统中相互关联变量之间的复杂交互，并从迭代消息的不动点中提取信息，为处理优化、推理和学习问题中的困难计算任务提供了一个强大的工具包。约束满足问题(Constraint Satisfaction Problems, CSPs)是复杂系统研究中最典型的计算任务之一，CSPs的一个基本计算问题是，在给定实例中找到满足所有约束的变量赋值的存在性和数量。在理论计算机科学的计算复杂性理论中，许多原型NP-难问题可以被表述为CSPs，因此CSPs被广泛研究和讨论。

许多学者开始利用消息传递算法求解约束满足问题，如利用消息传递算法中的置信传播(belief propagation, BP)算法求解约束满足问题，得到了很好的求解效率。由于RB模型是一个典型的具有可变取值域的随机约束满足问题模型，且具有精确相变，所以RB模型一经提出，就受到广泛关注，得到国内外学者的重视，并针对RB模型进行了大量的理论和实验研究。文献 [1] [2] 提出几种不同的置信传播(belief propagation, BP)算法求解RB模型产生的随机实例。文献 [3] 提出改进的置信传播算法，在BP方程中加入惩罚值，使得算法可以更有效的求解最大约束满足问题。文献 [4] 提出置信传播和模拟退火相结合的算法求解RB模型。相关文献 [5] 中，提出一种基于异步更新的置信传播算法求解RB模型，改变BP算法消息更新过程，极大的提高了算法的求解效率。文献 [6] 提出一种基于残差的消息传递算法，选择具有最大残差的边更新信息，算法提高了BP算法的收敛性和性能。

本文基于文献 [1] 中的算法3，考虑置信传播方程不收敛时，为了使算法可以继续下去，提出基于回溯的置信传播算法(backtracking belief propagation, BBP)来提高算法的收敛性。在BBP算法中，若迭代收敛，则根据变量的边际概率分布选取具有最大边际概率的变量，将其值固定在边际概率最大的分量上，同时将该变量的各取值分量按照边际概率降序依次排序，以此作为该变量的取值顺序；若迭代不收敛后，则进行回溯，改变上一个变量的值，重新进行迭代。数值结果表明：与BP算法相比，BBP算法通过回溯可以找到更多的有解实例，有效提高随机实例的求解概率。

2. RB模型

过去几十年，针对CSP的研究，主要集中在A，B，C，D四种标准模型 [7] [8] [9] 上。后来Achlioptas等人发现随着问题规模的增大，很难找到一组赋值同时满足所有约束，即模型会表现出平凡渐近无解性 [10] 。为解决这一问题，学者们先后从多个角度提出各种不同改进模型 [10] [11] [12] [13] [14] ，其中包括RB (Revised B)模型 [11] ，RB模型对B模型约束数量和取值域大小进行了限制。文献 [11] 证明了RB模型存在精确的可满足性相变现象。而且RB模型在相变区域会产生大量的难解实例 [15] [16] 。

RB模型的一个随机实例由变量集合 $X=\left\{x_1,x_2,\cdots ,x_N\right\}$ 和约束集合 $C=\left\{C_1,C_2,\cdots ,C_M\right\}$ 组成。每个变量都有对应的定义域 $D=\left\{s_1,s_2,\cdots ,s_d\right\}$ ，其中 $\left|D\right|=d$ ， $d=N^{\alpha }$ ( $\alpha >0$ 是常数)。每个约束 $C_i$ 包含 $k\left(k\ge 2\right)$ 个不同的变量。对于每个约束 $C_i$ ，定义 $Q_i$ 为k个变量的不相容赋值，即若这k个变量的取值属于集合 $Q_i$ ，则约束是不可满足的；否则约束就是可满足的。求解RB模型的一个实例，相当于找到实例中N个变量的一组赋值，使得所有约束同时被满足。生成RB模型的随机实例的步骤如下 [11] ：

a) 从可能的 $C_N^k$ 个约束中随机、可重复地挑选 $M=rN\ln N$ 个约束构成约束集合 ${\left\{C_i\right\}}_{i=1}^M$ ，每个约束 $C_i$ 都包含从N个变量中随机、不可重复挑选的k个变量；

b) 对每个约束 $C_i$ ，从 $d^k$ 个可能赋值中随机、不可重复地选取 $p{d}^k$ 个构成不协调赋值集合 $Q_i$ ，这里 $0<p<1$ 表示约束紧度。

文献 [11] 中严格证明了RB模型存在精确的可满足性相变现象。用 $\mathrm{Pr}\left(\text{SAT}\right)$ 表示RB模型的随机实例有解的概率，则有以下结论成立：

定理1 [11] 令 $p_s=1-{\text{e}}^{-\frac{\alpha }{r}}$ ，如果 $\alpha >\frac{1}{k},r>0$ 是两个常数，且 $k{\text{e}}^{-\frac{\alpha }{r}}\ge 1$ ，则

$\underset{N\to \infty }{\lim }\mathrm{Pr}\left(\text{SAT}\right)=\{\begin{array}{l}1,p<p_s\\ 0,p>p_s\end{array}$ (1)

定理表明RB模型在临界值 $p_s$ 处的可满足概率发生突变，当 $N\to \infty$ 时，若 $p<p_s$ ，RB模型的随机实例有解的概率趋近于1；若 $p>p_s$ ，RB模型的随机实例有解的概率趋近于0。

3. 基于回溯的置信传播算法

3.1. RB模型的因子图

因为 $k\ge 2$ 时RB模型都是NP-完全问题，所以为了方便讨论，本文讨论 $k=2$ 时的RB模型。二元RB模型的部分因子图如图1所示，图中的圆圈表示变量结点，记作 $i,j,k,\cdots$ ，图中的方块表示约束结点，记作 $a,b,c,\cdots$ ，约束与约束中包含的变量的结点之间用线相连，表示一条边。

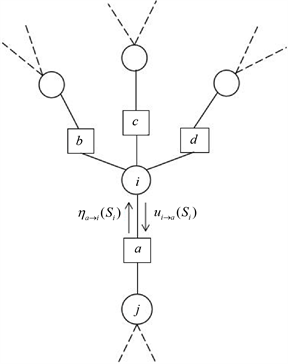
Figure 1. Partial factor graphs of random instances of binary RB model

图1. 二元RB模型随机实例的部分因子图

3.2. BP迭代方程

因子图中每条边 $\left(a,i\right)$ 上定义了两种信息，分别是约束a发送给变量i的信息 ${\eta }_{a\to i}\left(s_i\right)$ 和变量i发送给约束a的信息 $u_{i\to a}\left(s_i\right)$ ， ${\eta }_{a\to i}\left(s_i\right)$ 表示约束a要求变量i取值为 $s_i$ 的概率； $u_{i\to a}\left(s_i\right)$ 表示变量i在没有约束a的情况下取值为 $s_i$ 的概率。根据统计物理学中的空腔场理论，可得到BP迭代方程：

$u_{i\to a}^t\left(s_i\right)=\frac{1}{Z^{i\to a}}{\displaystyle \underset{b\in V\left(i\right)\backslash a}{\prod }{\eta }_{b\to i}^t\left(s_i\right)}$ (2)

${\eta }_{a\to i}^{t+1}\left(s_i\right)=\frac{1}{Z^{a\to i}}{\displaystyle \underset{s_j\in D,j\in V\left(a\right)\backslash i}{\sum }\delta \left(s_i,s_j\right)u_{j\to a}^t\left(s_j\right)}$ (3)

其中

$\delta \left(s_i,s_j\right)=\{\begin{array}{l}0,\left(s_i,s_j\right)\in Q_a\\ 1,\left(s_i,s_j\right)\notin Q_a\end{array}$ (4)

这里 $Z^{i\to a}$ 和 $Z^{a\to i}$ 是归一化因子， $V\left(i\right)$ 表示与变量i相关的所有约束， $V\left(i\right)\backslash a$ 表示与变量i相关的约束除去约束a； $V(a)$ 表示约束a中包含的所有变量， $V\left(a\right)\backslash i$ 表示约束a包含的变量除去变量i。

3.3. BBP算法

事实上，文献 [1] 中提出的算法，在接近相变点会出现BP方程不收敛的情况，导致算法失效，为了提高算法地求解效率，在算法中加入回溯算法，得到BBP算法。当BP算法不收敛时，通过回溯增加算法收敛的可能性，最后找到满足约束的一组赋值。

置信传播算法是在BP方程收敛后，计算每个变量取值的边际概率分布，每一步只将一个具有最大边际概率的变量的值固定到其概率最大的分量上，因此在算法执行过程中，将变量分为三种类型，如图2所示：

A类型：已赋值的变量；

B类型：与A类型的变量在同一个约束中的变量；

C类型：其它变量；

Figure 2. Type of variable during algorithm execution

图2. 算法执行过程中的变量类型

BBP算法步骤：

输入：二元RB模型一个随机实例的因子图，BP方程的最大迭代次数 $t_{\max }$ ，精度 $\epsilon$ 和最大回溯次数 $T_m$ 。

输出：实例的解或者算法不收敛。

Step 1： $n=1$ ， $T=0$ ，运行子程序BP算法得到 ${\eta }_{a\to i}^{\ast }\left(s_i\right)$ ；

Step 2：计算每个变量i的取值的边际概率

${\eta }_i\left(s_i\right)=\frac{{\displaystyle \underset{a\in \partial i}{\prod }{\eta }_{a\to i}^{\ast }\left(s_i\right)}}{{\displaystyle \underset{s_i\in D}{\sum }{\displaystyle \underset{a\in \partial i}{\prod }{\eta }_{a\to i}^{\ast }\left(s_i\right)}}}$ (5)

Step 3：挑选所有 ${\eta }_i\left(s_i\right)$ 中的最大值，将其所对应的变量i作为第一个待赋值的变量 $x_1$ ，将 $x_1$ 的值固定在分量 $s_i$ 上，并将 $x_1$ 的所有取值按边际概率降序排列，得到该变量的一个取值顺序 $V_{x_1}$ 。

Step 4： $n=n+1$ ， $t=0$ ，初始化每条边上约束发送给变量的信息 ${\eta }_{a\to i}^{\left(0\right)}\left(s_i\right)$ ：

对于A类型的变量：跳过；

对于B类型的变量：如果变量i的取值 $s_i$ 与约束中A类型的变量j的取值满足 $\left(s_i,s_j\right)\in Q_a$ ，则 ${\eta }_{a\to i}^{\left(0\right)}\left(s_i\right)=0$ ；否则， ${\eta }_{a\to i}^{\left(0\right)}\left(s_i\right)=1$ ；

对于C类型的变量：随机初始化 ${\eta }_{a\to i}^{\left(0\right)}\left(s_i\right)$ ；

Step 5： $t=t+1$

对于A类型的变量：跳过；

对于B类型的变量： ${\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)={\eta }_{a\to i}^{\left(t-1\right)}\left(s_i\right)$ ；

对于C类型的变量：将 ${\eta }_{a\to i}^{\left(t-1\right)}\left(s_i\right)$ 代入公式(2)计算得到 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)$ (如果 $V\left(i\right)\backslash a=\varphi$ ，则令 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)=1/d$ )，然后将 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)$ 代入公式(3)更新得到 ${\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)$ ；

Step 6：如果 $\left|{\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)-{\eta }_{a\to i}^{\left(t-1\right)}\left(s_i\right)\right|<\epsilon$ ，则令 ${\eta }_{a\to i}^{\ast }\left(s_i\right)={\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)$ ，并执行Step 8；否则，执行Step 5；

Step 7：如果 $t=t_{\max }$ ，则BP方程不收敛，令 $n=n-1$ ，执行Step 10；

Step 8：对于B类型和C类型的变量，利用公式(5)计算变量取值的边际概率；

Step 9：挑选所有 ${\eta }_i\left(s_i\right)$ 中的最大值，将其所对应的变量i作为第n个待赋值的变量 $x_n$ ，并将 $x_n$ 的值固定在分量 $s_i$ 上。同时将 $x_n$ 的所有取值按边际概率降序排列，得到该变量的一个取值顺序 $V_{x_n}$ 。检查此次赋值是否满足所有约束，如果不满足约束则输出未找到实例的解；

Step 10： $T=T+1$ ，如果 $T>T_m$ ，则输出没找到实例的解；否则，执行Step 11；

Step 11：根据变量 $x_n$ 的取值顺序 $V_{x_n}$ ，如果 $V_{x_n}$ 中还有值未被取过，则将 $V_{x_n}$ 中当前取值的后一位赋给 $x_n$ ，并检查此次赋值是否满足所有约束，如果该不满足约束则执行Step 10；如果 $V_{x_n}$ 中所有值都被取过，则清除该变量的取值，且 $n=n-1$ ，如果 $n<1$ ，则输出没找到实例的解，如果 $n\ge 1$ ，则执行Step 10；

Step 12：如果 $n<N$ ，执行Step 7；如果 $n=N$ ，则找到上满足约束的一组赋值，并输出这组赋值作为实例的解。

子程序BP算法如下：

Step 1： $t=0$ ，随机初始化每条边上约束发送给变量的信息 ${\eta }_{a\to i}^{\left(0\right)}\left(s_i\right)$ ；

Step 2： $t=t+1$ ，将 ${\eta }_{a\to i}^{\left(t-1\right)}\left(s_i\right)$ 代入公式(2)计算得到 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)$ (如果 $V\left(i\right)\backslash a=\varphi$ ，则令 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)=1/d$ )，然后将 $u_{i\to a}^{\left(t-1\right)}\left(s_i\right)$ 代入公式(3)更新得到 ${\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)$ ；

Step 3：如果 $\left|{\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)-{\eta }_{a\to i}^{\left(t-1\right)}\left(s_i\right)\right|<\epsilon$ ，则令 ${\eta }_{a\to i}^{\ast }\left(s_i\right)={\eta }_{a\to i}^{\left(t\right)}\left(s_i\right)$ ,输出 ${\eta }_{a\to i}^{\ast }\left(s_i\right)$ ;否则，执行Step 2；

Step 4：如果 $t=t_{\max }$ ，则输出不收敛。

4. 数值结果及分析

在数值实验中，本文取 $N\in \left\{20,40,60,80,100\right\}$ ， $k=2$ ， $\alpha =0.8$ ， $r=3$ 生成100个二元RB模型的随机实例。对不同的变量数N，变量的定义域规模d和约束的数目M如表1所示。在算法中，取最大迭代次数 $t_{\max }={10}^3$ ，精度 $\epsilon ={10}^{-4}$ 。

Table 1. Parameter values of binary RB model under different number of variables

表1. 二元RB模型在不同变量数N下的参数值

4.1. 算法结果

在算法中，取最大回溯次数 $T_m=500$ 。在100个随机实例上运行BBP算法，算法求解概率如图3所示。

Figure 3. The result of solving 100 random instances by BBP algorithm

图3. BBP算法求解100个随机实例的结果

从图3可以看出，在 $N=20$ 时，BBP算法在 $p\le 0.16$ 时找到解的概率是100%，当 $p\ge 0.25$ 时算法找不到任何解；在 $N=100$ 时，BBP算法在 $p\le 0.19$ 时找到解的概率是100%，当 $p\ge 0.22$ 时算法找不到任何解。

4.2. 算法分析

$N=\left\{20,40,60\right\}$ 时，BBP算法和BP算法的求解效率对比分别如图4~6所示。

从图中可以看出，与BP算法相比，BBP算法可以明显提高对实例的求解概率，尤其是在区域 $0.18<p<0.22$ 内，BBP算法可以通过回溯找到更多的有解实例。

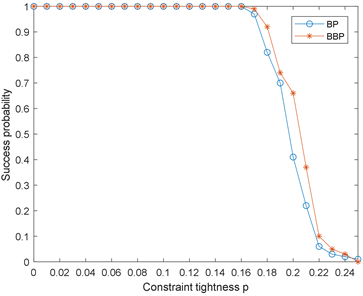
Figure 4. Comparison of the results of the two algorithms for N = 20

图4. N = 20时两种算法的结果对比

Figure 5. Comparison of the results of the two algorithms for N = 40

图5. N = 40时两种算法的结果对比

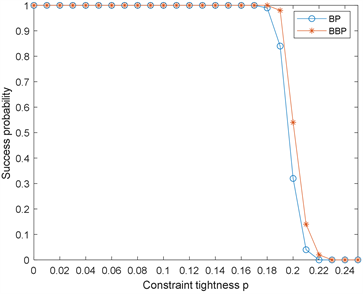
Figure 6. Comparison of the results of the two algorithms for N = 60

图6. N = 60时两种算法的结果对比

$N=\left\{20,40,60\right\}$ 时，BBP算法求解100个实例，未发生回溯找到解和发生回溯找到解的情况如图7~9所示。从图中可以看出，对于 $N=\left\{20,40,60\right\}$ ，在区域 $0.17\le p\le 0.23$ 内，BBP算法通过回溯有效提高算法的求解效率，当 $p>0.23$ 时，即使发生回溯也无法找到实例的解。值得注意的是，随着p的增大，发生回溯找到解的实例的数目呈现先增加再减少的趋势，在 $p=0.2$ 时，发生回溯找到解的实例的数目达到最大。

接下来，我们比较BBP算法和BP算法的收敛性。取 $N=20$ ，BBP算法和BP算法求解100个实例时收敛的实例数对比如图10所示。图10表明BBP算法的收敛性优于BP算法的收敛性，说明通过回溯可以提升算法的收敛性，从而提高算法的求解效率。

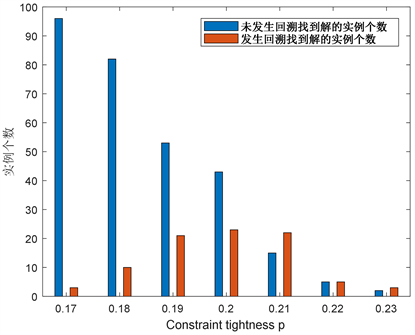
Figure 7. The backtracking when the BBP algorithm finds the solution for N = 20

图7. $N=20$ 时BBP算法找到解的回溯情况

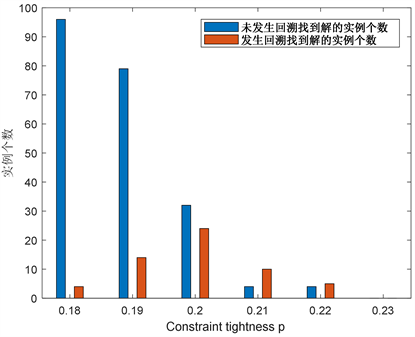
Figure 8. The backtracking when the BBP algorithm finds the solution for N = 40

图8. $N=40$ 时BBP算法找到解的回溯情况

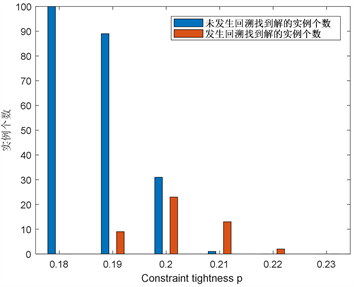
Figure 9. The backtracking when the BBP algorithm finds the solution for N = 60

图9. N = 60时BBP算法找到解的回溯情况

Figure 10. Comparison of the number of convergence cases between BP algorithm and BBP algorithm for N = 20

图10. N = 20时BP算法和BBP算法收敛的实例数目对比

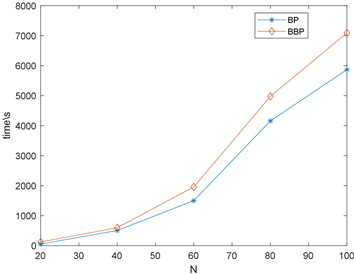
Figure 11. The running time of the two algorithms for p = 0.19

图11. $p=0.19$ 时两种算法求解的运行时间

在 $p=0.19$ 处BBP算法和BP算法求解RB模型的随机实例的运行时间对比如图11所示。

从图11可以看出，算法运行时间随着问题规模N的增加呈指数形式增长。BBP算法因为回溯策略的加入，算法的运行时间也明显增加，而且随着问题规模N的增加，BBP算法较BP算法增加的运行时间越来越多。

5. 总结

本文提出基于回溯的置信传播算法求解大值域的随机约束满足问题。算法在BP迭代方程不收敛时，通过回溯改变上一个变量的值，并重新进行迭代，保证消去变量的过程继续进行。数值结果表明，BBP算法可以提高BP算法的收敛性，与BP算法相比可以有效提高算法的求解效率。因为回溯的加入，算法的时间复杂度会增加，所以在未来的工作中，可以优化算法，减少算法的时间复杂度。