玻璃文物化学成分体系的统计分析

Statistical Analysis of the Chemical Composition System of Ancient Glass

摘要: 玻璃的起源历史悠久，作为中西方早期贸易、文化交流的宝贵物证之一，玻璃极大地丰富了人类的物质文化。分析玻璃文物类型和化学成分之间的关系，对玻璃制作工艺、来源等的研究具有非常重要的科学指导意义。本文对我国古代玻璃的化学成分进行了研究，首先使用线性回归分析和相关性分析确立了玻璃文物表面的风化化学成分，得到玻璃文物表面风化与类型的关系；然后使用K-means算法对玻璃文物进行亚类划分；最后综合均值法和偏最小二乘回归模型预测玻璃文物风化前化学成分含量，并基于决策树法鉴别未知玻璃文物所属的类型。本文对于古代玻璃文物的成分分析与类别鉴定具有一定的指导价值。

Abstract: Glass has a long history of origin. As one of the precious material evidence of the early trade and cultural exchanges between China and the West, glass has greatly enriched the material culture of human beings. The analysis of the relationship between the type and chemical composition of glass cultural relics is of great scientific guiding significance to the research of glass production technolo-gy and source. This paper studies the ancient Chinese glass. Firstly, we use the linear regression analysis and the correlation analysis to establish the weathering chemical composition of the glass artifact surface and obtain the relationship between surface weathering and type of glass cultural relics. Then, we use the K-means algorithm to subclassify the glass artifacts. Finally, we combine the mean method and partial least squares regression model to predict the pre-weathering chemical content of glass relics, and identify the type of unknown glass relics based on the decision tree method. This paper has certain guiding value for the composition analysis and category identifica-tion of ancient glass cultural relics.

1. 引言

古代玻璃的起源历史悠久，作为中西方早期贸易、文化交流的宝贵物证之一，玻璃极大地丰富了人类的物质文化，同时，大量的古代玻璃制品存留至今。玻璃的主要原料是石英砂，化学成分为二氧化硅。纯石英砂的熔点较高，为了降低熔化温度，需要添加助熔剂。根据所添加助熔剂的不同，可以将我国早期的玻璃体系大致分为铅钡玻璃和高钾玻璃，又可以根据文物表面有无风化，继续划分为有风化铅钡玻璃、无风化铅钡玻璃、有风化高钾玻璃和无风化高钾玻璃。分析玻璃文物类型和化学成分之间的关系，对玻璃制作工艺、来源等的研究具有非常重要的科学指导意义，同时有利于为古代中西方物质文化交流提供科学依据。

公元前4000年，美索不达米亚和埃及地区就开始生产玻璃的雏形——费昂斯 [1] ，中国古代的玻璃体系较之晚了近2000年，玻璃制品在本土地区经历了从舶来品到自主生产的过程，但无论美索不达米亚、埃及还是中国，早期的玻璃制品皆以珠饰为主 [2] 。因此探究我国古代玻璃文物的化学成分体系和种类划分，是研究玻璃技术发展、来源的必经之路，在此基础上深入分析，也有利于探讨古代中西方之间的文化演进、贸易交流、人群迁徙等。

化学成分分析是研究古代玻璃制品成分体系不可或缺的重要一环。国内外对古代玻璃文物制品的研究，主要是围绕玻璃发展史和化学技术层面对玻璃文物进行化学成分检测展开的 [3] 。而对于数学统计层面，预测玻璃文物风化前后的类型和化学成分的文献较少。因此本文希望能够建立合适的数学模型，对玻璃文物风化前后的类型和化学成分进行预测。

我国出土的玻璃文物众多，对古代玻璃的发展史和化学成分检测的研究一直是重点问题。沈从文结合史料记载和对出土文物的考察提出“中国古代玻璃制作技术从颗粒装饰品逐渐转化成小件玻璃制品，至晚在战国晚期完成” [4] 。安佳瑶对玻璃的整体发展史进行概述，将中国古代玻璃进行阶段性分析 [1] 。干福熹带领团队从化学技术的层面对玻璃文物进行了大量检测技术的研究，主要采用PIXE和EDXRF的方法，证明了古代最早的高钾玻璃和铅钡玻璃产自中国，提出了中国玻璃“自创说”理论 [5] [6] [7] [8] [9] 。成倩等人利用微损的激光剥离技术对文物进行化学成分检测，对文物的损害很小 [10] 。随着科技的不断发展，化学成分分析向着快速、准确、无损的方向发展。

为了在数学统计层面建立更精准的模型对玻璃文物进行化学成分分析和类型鉴别，本文对高教社杯数学建模C题中提供的实验数据进行建模，使用SPSS、Python，通过回归分析、相关性分析、K-means算法和决策树等，确立了玻璃文物表面的风化化学成分，得到玻璃文物表面风化与类型的关系，预测风化前的化学成分含量；同时对高钾、铅钡玻璃进行亚类划分，进而鉴别未知玻璃文物所属的类型。

2. 成分体系

本章给出我国古代玻璃文物风化与化学成分之间的相关性分析，并对高钾、铅钡玻璃进行亚类划分。

我们收集到一批古代玻璃文物的相关数据在表单2中，进行数据预处理：1) 表单中空白处表示未检测到该化学成分，将其用0填充；2) 将成分比例累加之和不在85%~105%的数据删除；3) 将表单剔除异常值后的化学成分数据进行归一化处理，使其累加和为100%；4) 将“文物采样点”分开成“文物编号”和“采样点”，并对表单1和2进行合并。部分结果见如下图1：

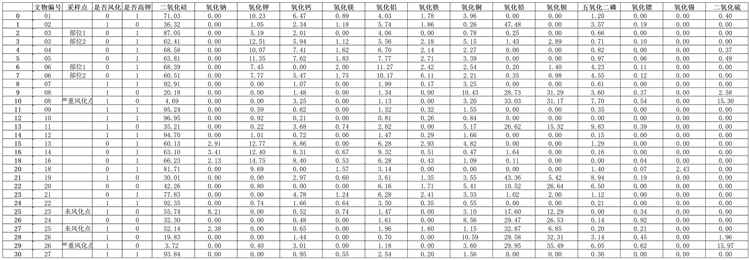
Figure 1. Part of the preprocessed experimental data

图1. 部分预处理后的实验数据

2.1. 相关性分析

要分析玻璃表面有无风化化学成分，采用多元线性回归分析与相关性分析相结合的方式。根据处理后的数据，以14个化学成分作为输入，是否风化作为输出，建立多元线性回归模型，计算14个指标的权重，规定大于某一阈值的为风化化学成分；同时进行相关性分析，验证我们所得结果的合理性。

2.1.1. 确定回归系数

令输入变量 $x_i\left(i=1,2,\cdots ,14\right)$ 分别表示十四种化学成分的百分含量，输出变量y表示是否风化。y = 1表示风化；y = 0表示没有风化。

建立多元线性回归分析模型：

$\{\begin{array}{l}y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_0{\beta }_0+\epsilon \\ \epsilon ~N\left(0,{\sigma }^2\right)\end{array}$

其中， ${\beta }_0,{\beta }_1,\cdots ,{\beta }_m,{\sigma }^2$ (m = 14)都是与 $x_1,x_2,\cdots ,x_m$ 无关的未知参数， ${\beta }_0,{\beta }_1,\cdots ,{\beta }_m$ 称为回归系数。

得到独立观测数据：

$\{\begin{array}{c}{b}_i={\beta }_0+{\beta }_1{\beta }_{i1}+\cdots +{\beta }_m{\beta }_{im}+{\beta }_i\\ {\epsilon }_i\text{~}N\left(0,{\sigma }^2\right),i=1,\cdots ,n\end{array}$

其中， $b_i$ 为y的观察值， $a_{i1},\cdots ,a_{im}$ 分别为 $x_1,x_2,\cdots ,x_m$ 的观察值，i = 1~n (n > m)。

记

$X=\left(\begin{array}{cccc}1& a_{11}& \cdots & a_{1m}\\ ⋮& ⋮& ⋮& ⋮\\ 1& a_{n1}& \cdots & a_{nm}\end{array}\right),Y=\left(\begin{array}{c}{b}_1\\ ⋮\\ b_n\end{array}\right)$

$\epsilon ={\left({\epsilon }_1,\cdots ,{\epsilon }_n\right)}^{\text{T}},\beta ={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_m\right)}^{\text{T}}$

可得

$\{\begin{array}{c}Y=X\beta +\epsilon \\ \epsilon ~N\left(0,{\sigma }^2{E}_n\right)\end{array}$

其中， $E_n$ 为n阶单位矩阵(n为数据的样本数)。

利用Python，将处理后的数据代入模型，进行模型的求解。根据以上模型建立过程，我们得到这14个化学成分对风化程度的权重及影响见如下表1：

Table 1. Regression coefficients of the multiple linear regression model

表1. 多元线性回归模型的回归系数

由表1，设置阈值为0.1，取绝对值大于0.1的化学元素即氧化钾(K₂O)，氧化钙(CaO)，氧化铁(Fe₂O₃)，氧化铅(PbO)，五氧化二磷(P₂O₅)，氧化锡(SnO₂)，并认为这些化学成分对风化程度的影响相对较大，其余可以近似忽略。

2.1.2. 基于Pearson相关系数的风化相关性热力图

在实际情况下，化学成分对风化程度的影响很难是完全线性的，且各成分之间必然存在互相影响的情况，因此我们在多元线性回归分析的基础上，进行了相关性分析来更全面地分析化学成分对风化程度的影响。

假设有两组数据 $X\left\{X_1,X_2,\cdots ,X_n\right\}$ 和 $Y\left\{Y_1,Y_2,\cdots ,Y_n\right\}$ (n = 15)。X和Y代表是否风化和14种化学成分。当表面风化时取1，没有发生风化时取0。

样本均值为：

$\bar{X}=\frac{{\displaystyle {\sum }_{i=1}^n{X}_i}}{n},\bar{Y}=\frac{{\displaystyle {\sum }_{i=1}^n{Y}_i}}{n}$

样本协方差：

$Cov\left(X,Y\right)=\frac{{\displaystyle {\sum }_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}}{n-1}$

样本Pearson相关系数 [11] ：

$r_{XY}=\frac{Cov\left(X,Y\right)}{S_X{S}_Y}$

其中， $S_X$ ， $S_Y$ 为样本标准差，公式如下：

$S_X=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(X_i-\bar{X}\right)}^2}}{n-1}},S_Y=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\bar{Y}\right)}^2}}{n-1}}$

采用SPSS绘制出各化学成分的Pearson相关系数，见如下图2：

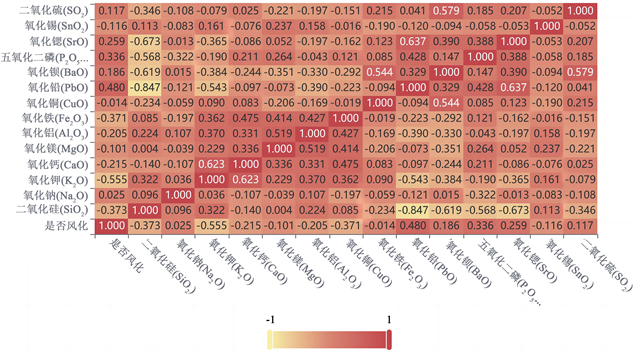
Figure 2. Heat map of chemical composition and weathering correlation

图2. 化学成分与风化相关性热力图

由图2，我们取阈值为0.2，满足风化系数大于0.2的有8种化学成分，结果见如下表2：

Table 2. Pearson Chemical composition with a correlation coefficient greater than 0.2

表2. Pearson相关系数大于0.2的化学成分

2.1.3. 总结

综合考虑，取两种的交集作为对风化程度有较大影响的化学成分：氧化钾(K₂O)，氧化钙(CaO)，氧化铁(Fe₂O₃)，氧化铅(PbO)，五氧化二磷(P₂O₅)。

最后，我们对五个风化化学成分和“类型是否为高钾玻璃”作风化相关性热力图，结果见如下图3：

由图3，可以发现：

1) 高钾玻璃风化程度与氧化钾、氧化钙、氧化铁含量关系成正相关，而铅钡玻璃的风化程度与氧化铅，五氧化二磷关系成正相关。

2) 在风化情况下，玻璃文物是高钾玻璃还是铅钡玻璃与氧化钾和氧化铅的含量有关。

3) 髙钾玻璃是否风化与氧化钾的占比含量相关性较强；铅钡玻璃是否风化与氧化铅的占比含量相关性较强。

Figure 3. Heat map of weathering chemical composition correlation

图3. 风化化学成分相关性热力图

2.2. 亚类划分

2.2.1. 确定分类中心

为了对高钾玻璃和铅钡玻璃进行更加细类的划分，我们可以采用聚类分析法。聚类分析是一种无监督学习，用于对未知类别的样本进行划分将它们按照一定的规则划分成若干个类簇，把相似(相关的)的样本聚在同一个类簇中，把不相似的样本分为不同类簇，从而分析样本之间内在的性质以及相互之间的联系规律。

K-means算法是基于划分的聚类算法，计算样本点与簇质心的距离，与簇质心相近的样本点划分为同一类簇。两个样本距离越远，则相似度越低。

基本流程：

1) 设定k值，表示需要将数据分成k个簇，从样本点中随机选择k个点作为初始簇中心。

2) 分别计算每个样本点到各个初始簇中心的距离，将每个样本点划分到距离它最近的中心点。

3) 用各簇中所有样本的质心(即为均值，向量的各个维度分别取平均)代替原有的中心点。

4) 重复步骤2和3，直到中心点不变或达到预定迭代次数时，算法终止。

迭代计算就是一个优化目标的过程，这是机器学习算法必不可少的一步，这里优化的是各个数据点到中心点的距离，距离越小越好。

根据预处理后的数据，利用python，我们可以得到高钾和铅钡玻璃分类的中心见如下表3：

Table 3. High potassium glass and lead barium glass classification center

表3. 高钾玻璃和铅钡玻璃分类的中心

由表3确定的类中心，利用实验数据验证，对比结果发现，67组数据中心正确判断了58组数据，正确率达86.6%。故根据上表和化学成分的占比含量，可以对高钾玻璃和铅钡玻璃进行较为准确的分类。

2.2.2. 对高钾、铅钡玻璃进行亚类划分

在2.2.1的基础上，我们先设定k = 3，使用python运行程序，得到玻璃亚类中心见如下表4、表5：

Table 4. High-potassium glass subclass center table

表4. 高钾玻璃亚类中心表

Table 5. Lead barium glass subclass center table

表5. 铅钡玻璃亚类中心表

表4、表5对高钾玻璃和铅钡玻璃进行了具体的划分。

2.2.3. 合理性和敏感性分析

我们可以采用计算误差平方和SSE、轮廓系数、CH指标来评估聚类分析的好坏，本文采用轮廓系数。

公式如下：

$S\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\max \left\{a\left(i\right),b\left(i\right)\right\}}$

其中， $a\left(i\right)$ 表示化学成分的内聚度，计算公式如下：

$a\left(i\right)=\frac{{\displaystyle {\sum }_{j\ne 1}^n\text{distance}\left(i,j\right)}}{n-1}$

其中j表示与样本i在同一亚类内的其他样本点，distance表示i与j的距离。 $a\left(i\right)$ 越小说明该类越紧密。 $b\left(i\right)$ 计算公式与 $a\left(i\right)$ 相类似。

$S\left(i\right)=\{\begin{array}{l}1-\frac{a\left(i\right)}{b\left(i\right)},a\left(i\right)<b\left(i\right)\\ 0,a\left(i\right)=b\left(i\right)\\ \frac{b\left(i\right)}{a\left(i\right)}-1,a\left(i\right)>b(\; i\; )\end{array}$

当 $a\left(i\right)<b\left(i\right)$ 时，类内距离小于类间距离，聚类更紧凑，S的值趋近于1。轮廓系数S的取值范围为[−1, 1]，轮廓系数越大，聚类效果越好 [12] 。

我们分别令k = 1，2，3，4，5，计算得到了各个情形下的轮廓系数，见如下图4：

Figure 4. Plot of the contour coefficient versus k

图4. 轮廓系数与k的关系图

由图4可知：

1) 髙钾玻璃的聚类效果要始终优于铅钡玻璃，分类结果更加合理；

2) 当k < 3时，轮廓系数随着k的增大而明显增大，当k > 3时，增大速度放缓且趋近于一定值，K-means聚类分析效果变化不大，分类结果已经较为良好，故k取3具有一定的合理性；

3) K-means聚类分析模型对k的取值的敏感度较大，故选择一个合适的k对聚类分析十分重要。

保持k = 3，改变化学成分个数，分析对聚类效果的影响。化学成分分别取14种，8种(二氧化硅，氧化钾，氧化钙，氧化铝，氧化铁，氧化铅，五氧化二磷，氧化锶)，5种(氧化钾，氧化钙，氧化铁，氧化铅，五氧化二磷)，结果见如下图5：

由图5可知：

1) 化学成分个数越多，聚类效果越好。

2) 利用第一问求得的与风化相关性较强的化学成分，基本能够对高钾玻璃和铅钡玻璃进行分类。

3) 三种情况下，高钾玻璃的聚类效果都要优于铅钡玻璃。

4) 轮廓系数随化学成分个数的变化幅度较大，故聚类分析对化学成分个数的敏感度较大。

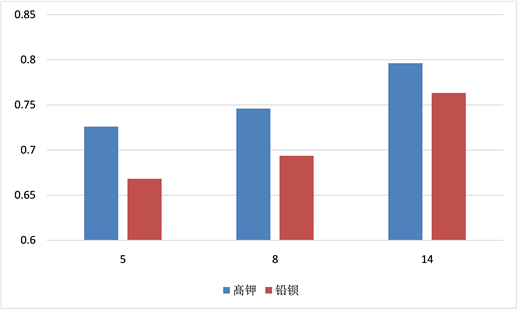
Figure 5. Diagaph of contour coefficient and number of chemical compositions

图5. 轮廓系数与化学成分个数的关系图

3. 模型建立

本章综合均值法和偏最小二乘回归模型预测玻璃文物风化前化学成分含量，并基于决策树法鉴别未知玻璃文物所属的类型。

3.1. 预测玻璃文物风化前化学成分含量

3.1.1. 均值法预测风化前化学成分含量

设不同类型的玻璃文物风化前的化学成分为 $c_{ij}$ ，具体表示第i次校验的第j个化学成分。

那么，

$C_j=\frac{1}{n_1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{c}_{ij},}\left(j=1,2,\cdots ,m\right)$

其中，m表示m种化学成分。

同理，设不同类型的玻璃文物风化后的化学成分为 $d_{ij}$ ，具体表示第 $i$ 次校验的第 $j$ 个化学成分。

那么，

$D_j=\frac{1}{n_2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{d}_{ij},}\left(j=1,2,\cdots ,m\right)$

易得知，风化过程的各化学成分的变化率

$E_j=\frac{C_j-D_j}{D_j}\times 100\%,\left(j=1,2,\cdots ,m\right)$

根据以上公式对实验数据进行处理，分别得到高钾玻璃和铅钡玻璃风化前后各个化学成分的均值以及变化率，结果见如下表6。

由表6我们对给定风化后数据的部分进行还原，使用公式

$C_j=D_j\left(1+E_j\right)$

即可得到不同类型的玻璃文物风化前的化学成分含量。

Table 6. Mean value and rate of change of each chemical composition before and after weathering

表6. 风化前后各化学成分的均值及变化率

3.1.2. 偏最小二乘回归分析模型预测风化前化学成分含量

本文我们建立偏最小二乘回归分析模型预测风化前化学成分含量 [13] ：

设风化后14种化学成分含量为 $x_i\left(i=14\right)$ ，风化前14种化学成分含量为 $y_i\left(i=14\right)$ 。自变量的观测数据矩阵记为 $A={\left(a_{ij}\right)}_{n\ast n}$ ，因变量的观测数据矩阵记为 $B={\left(B_{ij}\right)}_{n\ast n}$ 。n为训练集的样本个数。

1) 数据标准化。将各指标值 $a_{ij}$ 转化为标准化指标值 ${\tilde{a}}_{ij}$ ，有

${\tilde{a}}_{ij}=\frac{a_{ij}-{\mu }_j{}^{\left(1\right)}}{s_j{}^{\left(1\right)}},i=1,2,\cdots ,n.j=1,2,\cdots ,14.$

其中： ${\mu }_j{}^{\left(1\right)}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{a}_{ij}}$ ； $s_j^{\left(1\right)}=\sqrt{\frac{1}{n-1}{{\displaystyle {\sum }_{i=1}^n\left(a_{ij}-{\mu }_{ij}^{\left(1\right)}\right)}}^2}$ ，即 ${\mu }_j^{\left(1\right)}$ ， $s_j^{\left(1\right)}$ 为第j个自变量 $x_j$ 的样本均值和样本标准差。

对应地，称

${\tilde{x}}_j=\frac{x_j-{\mu }_j^{\left(1\right)}}{s_j^{\left(1\right)}},j=1,2,\cdots ,14.$

为标准化指标变量。

类似的，将 $b_{ij}$ 转化为标准化指标值 ${\tilde{b}}_{ij}$ ，有

${\tilde{b}}_{ij}=\frac{b_{ij}-{\mu }_j^{\left(2\right)}}{s_j^{\left(2\right)}},i=1,2,\cdots ,n.j=1,2,\cdots ,14.$

其中 ${\mu }_j^{\left(2\right)}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{b}_{ij}}$ ； $s_j^{\left(2\right)}=\sqrt{\frac{1}{n-1}{{\displaystyle {\sum }_{i=1}^n\left(b_{ij}-{\mu }_{ij}^{\left(2\right)}\right)}}^2}$ ，即 ${\mu }_j^{\left(2\right)}$ ， $s_j^{\left(2\right)}$ 为第j个因变量 $y_j$ 的样本均值和样本标准差。

对应地，称

${\tilde{y}}_j=\frac{y_j-{\mu }_j^{\left(2\right)}}{s_j^{\left(2\right)}},j=1,2,\cdots ,14.$

为标准化指标变量。

利用corrcoef函数求得28个变量之间的相关系数矩阵。进而分别提出标准化后自变量组 ${\tilde{x}}_j$ 和因变量组 ${\tilde{y}}_j$ 的数据。

求两个成分对时标准化指标变量与成分变量之间的回归方程。求得自变量组 ${\tilde{x}}_j$ 与因变量组 ${\tilde{y}}_j$ 之间的回归方程。最后将标准化变量 ${\tilde{x}}_j$ 、 ${\tilde{y}}_j$ (j = 1, 2)分别还原为原始变量 $x_j$ 、 $y_j$ ，得到回归方程。

3.1.3. 模型的求解

根据求得的风化前后各化学成分的均值及变化率，可以分析得到高钾、铅钡玻璃的分类规律有如下几点：

1) 对于高钾玻璃，风化后只有二氧化硅的含量大幅上升，其他化学成分含量都显著降低，大部分化学成分含量可以忽略不计。

2) 对于铅钡玻璃，风化后氧化钠、氧化钙、氧化镁、氧化铝、氧化铜、氧化铅、五氧化二磷、氧化锶、二氧化硫占比含量变多，其余变低。

通过Matlab，求得偏最小二乘回归分析部分回归系数直方图，见如下图6、图7：

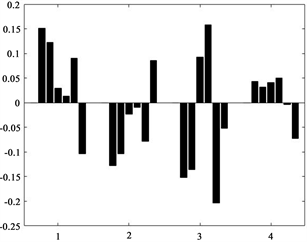
Figure 6. Histogram of partial least squares regression

图6. 偏最小二乘回归部分回归系数直方图

Figure 7. Fitting results of the regression equation

图7. 回归方程的拟合结果

由图6、图7可知，利用得到的回归方程去检验均值法预测出来的风化前化学成分含量的结果，拟合优度R² = 0.8143，拟合效果较高，说明均值法所得结果较为合理。能够根据风化点的检测数据，预测风化前14种化学成分的含量。

3.2. 鉴别未知玻璃文物所属类型

3.2.1. 决策树法鉴别未知玻璃文物的类型

决策树是通过对训练样本进行归纳学习生成决策树或决策规则，然后使用决策树或决策规则对新数据进行分类的一种数学方法。决策树是一个树型结构，它由一个根结点、一系列内部结点及叶结点组成，每一结点只有一个父结点和两个或多个子结点，结点间通过分支相连。决策树的每个内部结点对应一个非类别属性或属性的集合(也称为测试属性)，每条边对应该属性的每个可能值。决策树的叶结点对应一个类别属性值，不同的叶结点可以对应相同的类别属性值 [14] 。

决策树的生成通常采用自顶向下的递归方式，在构造过程中，采用信息增益度量。信息增益最大表明了数据集中在分类过程中能够最大化减少不确定性，因此具有更好的分类效果。信息熵(H)以及信息增益(G)可定义如下：

$H_{\left(p\right)}=-{\displaystyle \sum p\times \log p}$

$H_{\left(Y|X\right)}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_i{H}_{\left(Y|X=X_i\right)}}$

$G_{\left(D,A\right)}=H_{\left(D\right)}-H_{\left(D|A\right)}$

其中p表示随机变量的概率，A表示特征，D表示数据集， $H_{\left(D\right)}$ 表示经验熵， $H_{\left(Y|X\right)}$ 表示条件熵， $H_{\left(D|A\right)}$ 表示特征A在数据集D的条件下的经验条件熵。

3.2.2. 模型求解

利用SPSS，将预处理后的数据，以化学成分和玻璃文物表面是否风化作为输入，类型作为模型的输出，训练决策树模型。最后将实验数据附件表单3 [15] 中未知玻璃类别的化学成分和表面风化作为输入，预测最终结果见如下表7：

Table 7. Identification results of glass relics by decision tree method

表7. 决策树法对玻璃文物的鉴别结果

3.2.3. 准确性和灵敏性分析

利用SPSS，分别训练逻辑回归、向量机、随机森林模型，并与决策树法所预测结果相比较。结果见如下表8：

Table 8. Identification results of glass artifacts by the four models

表8. 四种模型对玻璃文物的鉴别结果

由图可知，四种模型对实验数据附件表单3 [15] 中未知玻璃文物所属类型的鉴别结果完全一致。

在前面求得高钾玻璃和铅钡玻璃类中心的基础上，求未知玻璃的化学成分与类中心的欧氏距离，比较他们匹配程度的差异性，进而进行灵敏度分析。

设玻璃文物的化学成分为 $P_i\left(i=1,2,\cdots ,14\right)$ ，高钾玻璃化学成分的类中心为 $Q_{1i}$ ，铅钡玻璃化学成分的类中心为 $Q_{0i}$ 。

则要求欧式距离之和尽量的小，即

$\min d={\displaystyle \underset{1}{\overset{14}{\sum }}\left|P_i-Q_i\right|}$ 。

代入Matlab计算结果见如下表9：

Table 9. Sensitivity analysis of the classification results

表9. 分类结果的灵敏度分析

由表9可知：

1) 欧氏距离分析得到的结果与逻辑回归、决策树、向量机、随机森林相一致。

2) 鉴别未知玻璃文物属性对二氧化硅、氧化钾、氧化铅的敏感性较大，对其他化学成分的敏感性较小。

4. 结论

本文对所给的实验数据进行数据预处理，分析并建立数学模型，研究了玻璃文物表面有无风化化学成分含量的统计规律和不同类别玻璃文物样品化学成分之间的关联关系，并根据风化点检测数据预测玻璃文物风化前的化学成分含量，鉴别给定的玻璃文物的类别。

首先，我们将多元线性回归分析和相关性分析相结合，探讨了玻璃文物化学成分和表面风化之间的统计关系，发现对风化程度有较大影响的化学成分有五种：氧化钾(K₂O)，氧化钙(CaO)，氧化铁(Fe₂O₃)，氧化铅(PbO)，五氧化二磷(P₂O₅)。

然后，基于玻璃文物风化与化学成分存在相关性的结论，采用K-means聚类分析算法确定类中心，并对高钾玻璃和铅钡玻璃进行更加细致的亚类划分。

最后，基于不同类别玻璃文物样品化学成分之间的关联关系，将均值法和偏最小二乘回归分析模型相结合，建立了玻璃文物化学成分预测模型，根据风化点的检测数据，预测了风化前14种化学成分的含量。并基于决策树法建立了玻璃类型鉴别模型，利用欧式距离分析发现，所建立的鉴别模型准确率较高。本文对于古代玻璃文物的成分分析与类别鉴定具有一定的指导价值。