基于分子动力学的磁流体抛光液剪切粘度数值模拟

Numerical Simulation of Shear Viscosity of Magnetic Fluid Polishing Liquid Based on Molecular Dynamics

摘要: 为探究纳米尺度机制对磁流体抛光液剪切粘度增强的影响。基于分子动力学模拟研究，以探索铁纳米颗粒的布朗运动和铁纳米颗粒团聚的形成等纳米机制，并研究它们对纳米流体(Fe-H2O)中剪切粘度增强的影响。使用SPC/E水模型对水体系建模，并通过分子动力学结合Muller-Plathe算法计算剪切粘度。此外，该数值研究在300 k温度下0.05%、0.54%、1.5%和4.3%的不同铁体积分数下进行。结果表明，由于铁纳米颗粒之间的相互作用形成团聚，纳米流体(Fe-H2O)的剪切粘度随着铁体积分数的增大而升高。

Abstract: In order to explore the influence of nanoscale mechanism on shear viscosity enhancement of mag-netic fluid polishing solution, based on the molecular dynamics simulation research, to explore the Brownian motion of iron nanoparticles and the formation of iron nanoparticles agglomeration and other nano mechanisms, and to study their effects on the shear viscosity enhancement in nanofluids (Fe-H2O). The SPC/E water model was used to model the water system, and the shear viscosity was calculated through molecular dynamics combined with Muller Plathe algorithm. In addition, the numerical study was carried out at 300 k with different iron volume fractions of 0.05%, 0.54%, 1.5% and 4.3%. The results show that the shear viscosity of nanofluids (Fe-H2O) increases with the in-crease of iron volume fraction due to the agglomeration formed by the interaction between iron nanoparticles.

1. 引言

近些年来，随着纳米技术飞速发展，其在各个领域的应用也越来越广泛。其中纳米流体的研究是重要领域之一，纳米流体是指把金属或非金属纳米粉体分散到水、醇、油等传统换热介质中，制备成均匀、稳定、高导热的新型换热介质，这是纳米技术应用于热能工程这一传统领域的创新性的研究 [1] 。同时，在纳米流体应用领域中的磁流体在加工抛光领域的应用也越来越受到人们的关注 [2] ，因此，包括导热系数和剪切粘度在内的物理性质是研究流动液体传热和流体力学性能的重要参数。剪切粘度表征了水性纳米流体对纳米颗粒流动的内部阻力。由于这些原因，在过去几年中进行了多项实验研究，以研究水基纳米流体的剪切粘度 [3] [4] [5] 。所有这些研究表明，纳米颗粒如金属纳米颗粒、氧化物纳米颗粒、石墨烯纳米片或碳纳米管在纯水中的悬浮液显著提高了水基纳米流体的剪切粘度。此外，纳米流体中的剪切粘度增强归因于纳米流体中在纳米尺度上发生的各种机制。然而，纳米尺度机制对纳米流体剪切粘度增强的影响仅在实验中被假设，并且无法得到证实。因为对纳米流体的研究由于缺乏适当的设备或过于复杂的条件，在纳米尺度上研究一些课题可能会很困难，计算机模拟目前是一种比较合适的方法，特别是分子动力学模拟，其在研究材料的化学和物理性质领域已经成为很有效的数值模拟技术。Razmara [6] 等人采用Green-Kubo算法利用分子动力学计算加入碳纳米管的纳米流体，在不同温度和不同体积分数下的剪切粘度，发现并得到水–碳纳米管纳米流体的剪切粘度和体积分数之间的关系式。Loulijat [7] 等人运用分子动力学研究布朗运动和界面层对纳米流体(Au-H₂O)粘度影响，研究在不同温度下纳米流体(Au-H₂O)的粘度变化以及金纳米颗粒表面的水分子数量分布变化。Heyhat [8] 等人通过分子动力学模拟含银纳米颗粒的水基纳米流体，研究纳米层对两种重要纳米流体性质的影响。研究发现，有序液体纳米层的形成导致基础流体收缩。将纳米流体做为是三组分混合物，提出了一种新的三元混合物关系来计算纳米流体密度，所得结果揭示了纳米层效应对纳米流体密度的重要性。此外，分析了液体分层在纳米流体粘度中的作用。Li [9] 等人为了理解纳米流体的粘度和导热性的显著增强，使用分子动力学模拟方法研究不同体积分数和温度的水铜纳米流体的热导率和粘度，以及界面层的结构和厚度，对纳米流体的结构和传输特性提供有用的见解。Shi [10] 将各种形状的Fe纳米颗粒插入H₂O分子中，以研究H₂O/Fe纳米流体的原子和热性能，模拟结构的原子和热行为通过势能、热导率、密度、速度和温度分布体现。

由于实验条件的限制，无法在原子尺度下直观了解纳米流体内部结构变化，计算机模拟成为研究的重要方法。在该数值分析中，通过使用分子动力学，研究铁纳米颗粒的纳米尺度机制对纳米流体(Fe-H₂O)中剪切粘度增强的作用。此外，将分子动力学模拟与Muller-Plathe算法应用于预测纳米流体(Fe-H₂O)的剪切粘度。

2. 分子动力学模拟细节

2.1. 计算方法

在该数值研究中，使用分子动力学模拟含铁纳米颗粒的水基纳米流体，以通过Muller-Plathe [11] 算法计算剪切粘度，并研究铁纳米颗粒的布朗运动的纳米尺度机制对纳米流体中剪切粘度增强的影响。分子动力学模拟是基于经典牛顿力学，评估相互作用原子的演化动力学，其由相互作用原子运动的数值积分方程控制。此外，分子动力学模拟的准确性与用于模拟原子间相互作用的势函数以及用于模拟纳米流体(Fe-H₂O)中分子之间相互作用的势能函数密切相关。由于纳米流体(Fe-H₂O)是铁纳米颗粒在纯水中的悬浮液，这意味着分子动力学需要对氧(O)、氢(H)和铁(Fe)之间的所有原子间相互作用以及水分子相互作用(H₂O)进行建模。因此，如图1使用SPC/E [12] 模型对纯水进行建模。

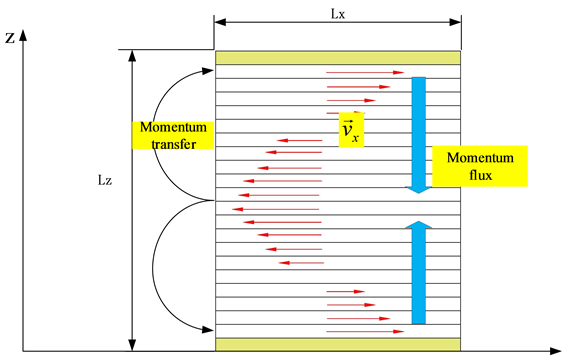
Figure 1. Schematic diagram of periodic simulation system

图1. 周期性模拟体系示意图

Lennard-Jones [13] (LJ)势函数计算范德华力、额外附加阻尼因子的库仑相互作用。pppm求解器计算长程库仑相互作用，如式(1)~(3)

$E_1=4{\epsilon }_{ij}\left[{\left(\frac{\sigma }{r_{ij}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}}\right)}^6\right]$ (1)

$E_2={\displaystyle \underset{i}{\sum }{\displaystyle \underset{j}{\sum }\frac{K_c{q}_i{q}_j}{r_{ij}}}}$ (2)

$E_s=E_1+E_2$ (3)

$E_s$ 是总作用力， $E_1$ 是LJ相互作用力， $E_2$ 是库仑相互作用力， $K_c$ 是介电常数， ${\epsilon }_{OO}$ 、 $\sigma$ 分别是原子之间的Lennard-Jones epsilon和Lennard-Jones sigma， $q_i$ 和 $q_j$ 分别代表两个原子的电荷， $r_{ij}$ 代表i原子和j原子间的距离。SPC/E水分子模型的分子间相互作用对势和结构参数如表1，表2给出LJ势模拟铁原子之间的相互作用和水分子中氧原子和铁原子之间的相互作用的参数。对于铁纳米颗粒中铁原子之间的相互作用采用EAM嵌入原子势 [14] 来模拟，其计算公式如下：

Table 1. Intercomponent potential and structural parameters of water in SPC/E model

表1. SPC/E模型的水分子间对势和结构参数

Table 2. Parameters of Lennard-Jones [15] interaction in nanofluids (Fe-H2O)

表2. 纳米流体(Fe-H₂O)中Lennard-Jones [15] 相互作用的参数

$E_i=F_{\alpha }\left({\displaystyle \underset{j\ne i}{\sum }{\rho }_{\alpha \beta }\left(r_{ij}\right)}\right)+\frac{1}{2}{\displaystyle \underset{j\ne i}{\sum }{\varphi }_{\alpha \beta }\left(r_{ij}\right)}$ (4)

式中， $F_{\alpha }$ 为嵌入能， ${\rho }_{\alpha \beta }$ 为原子i相邻原子j的密度， ${\varphi }_{\alpha \beta }$ 为核心间排斥的短程相互作用对。

通过平衡分子动力学的Muller-Plathe方法计算剪切粘度，该方法计算粘度是通过构建剪切场并结合横向线性动量通量实现的，公式如下。

$j_z\left(p_x\right)=-\eta \frac{\partial v_x}{\partial z}$ (5)

其中 $j_z\left(p_x\right)$ 代表在一定时间内，动量 $p_x$ 的x分量， $\frac{\partial v_x}{\partial z}$ 是x方向速度在z方向上的梯度， $\eta$ 为剪切粘度。公式(5)经过变换得到公式(6)。

$\eta =-\frac{{\displaystyle \underset{transfer}{\sum }\left(p_{x,n/2+1}-p_{x,1}\right)}}{2\Delta t{L}_x{L}_y\left(\partial v_x/\partial z\right)}$ (6)

$L_x,L_y$ 分别代表模拟体系x,y方向的长度， $\Delta t$ 为模拟时间步，n代表模拟体系等分为偶数个的个数，如图2动量通量以非物理的方式施加在系统上。周期模拟框沿z坐标细分为n层。

$\text{e}=1.602176634\times {10}^{-19}C$ 是基本电荷

氧原子和铁原子之间的能量参数表示纳米颗粒与流体之间的相互作用强度。根据geometric混合法则来计算氧原子与铁原子之间作用参数如表2。其计算公式如式(7) (8)。

${\sigma }_{ij}=\sqrt{{\sigma }_i{\sigma }_j}$ (7)

${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j}$ (8)

Figure 2. SPC/E water molecular model

图2. SPC/E水分子模型

2.2. 模拟程序

通过分子动力学研究纳米流体(Fe-H₂O)中铁纳米颗粒的体积分数和颗粒团聚对剪切粘度的影响，需要创建一个模拟区域(图3)，初始模型为水分子和铁纳米颗粒分开静止放置，模型主要采用改变铁纳米颗粒数量和水分子数量来创建不同体积分数的纳米流体(Fe-H₂O)，之后通过弛豫使得颗粒自由分散到水介质中。单个铁纳米颗粒的直径为1 nm，水介质的密度设置为1000 kg/m³。其中铁的晶格类型为体心立方结构，晶格常数为2.86 Å。此外，铁原子和水分子的初始速度根据给定温度从高斯分布中随机采样。在所有情况下，系统中水介质首先在等温等压(NPT)系综下弛豫100 ps，包括铁纳米颗粒后再弛豫500 ps，使铁纳米颗粒随机分散在水介质中。通过分别使用Nose-Hoover恒温器和恒压器 [16] [17] [18] [19] ，使系统压力和温度保持恒定，并且模拟的时间步为1 fs。弛豫600 ps之后，在等温等体积(NVT)系综下运用Muller-Plathe算法计算剪切粘度。最终，在分子动力学模拟中，模拟体系在300 k温度下，以0.05%、0.54%、1.5%和4.3%的不同体积分数记录系统中所有原子和分子的位置和速度，同时保证直径为1 nm且铁原子数为59的铁纳米颗粒相同，具体详情如表3。此外，所有模拟均使用LAMMPS [20] 开源软件，并且模拟结果中水分子和铁纳米颗粒速度和位置坐标，通过使用开源可视化软件OVITO [21] 显示。

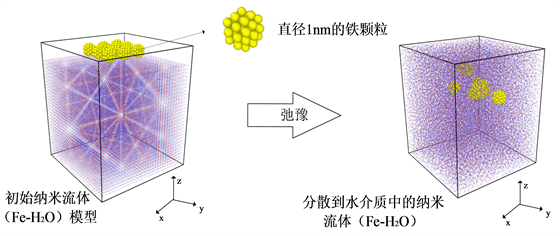
Figure 3. Initial model of nanofluids (Fe-H₂O)

图3. 纳米流体(Fe-H₂O)的初始模型

Table 3. Parameters of nanofluids (Fe-H2O) with different volume fractions

表3. 不同体积分数的纳米流体(Fe-H₂O)参数

3. 模拟结果和讨论

颗粒的布朗运动

铁纳米颗粒分散在水基纳米流体中，由于水分子在铁纳米颗粒的球形表面上的摩擦和碰撞，铁纳米颗粒开始在所有方向上移动并具有随机运动，则分散的铁纳米粒子在纯水中的随机运动称为布朗运动。图4，图5分别显示出300 k温度下不同体积分数的铁纳米流体在500 ps时间段内分散到纯水中的分布情况以及铁纳米颗粒的运动轨迹。图5中，0.05%铁纳米流体显示单个铁纳米颗粒在纯水中布朗运动轨迹，证实分散在纯水中的铁纳米颗粒的布朗运动。图4显示铁纳米颗粒在忽略重力的影响下，纳米颗粒受分子间相互作用力下从初始位置随机运动600 ps后的最终位置的纳米流体内部结构变化。图4(b)~(d)显示0.54%、1.5%、4.5%体积分数的铁纳米颗粒会在纯水中因受到纳米颗粒之间相互作用形成团聚，因为铁纳米颗粒数目不同和水分子数目不同影响颗粒之间的相互作用，导致不同体积分数铁纳米颗粒形成的纳米颗粒团聚不同。

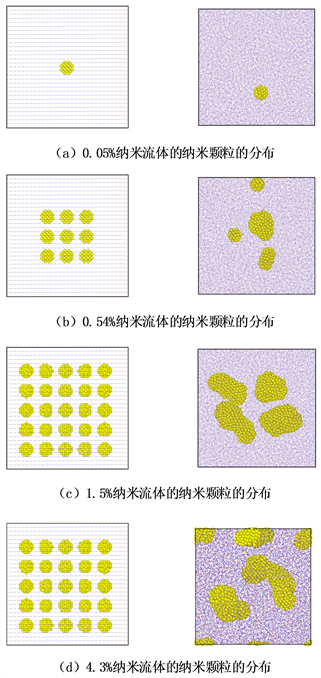
Figure 4. Particle distribution of nanofluids (Fe-H₂O) with different volume fractions on XY plane

图4. 在XY平面上不同体积分数纳米流体(Fe-H₂O)的颗粒分布

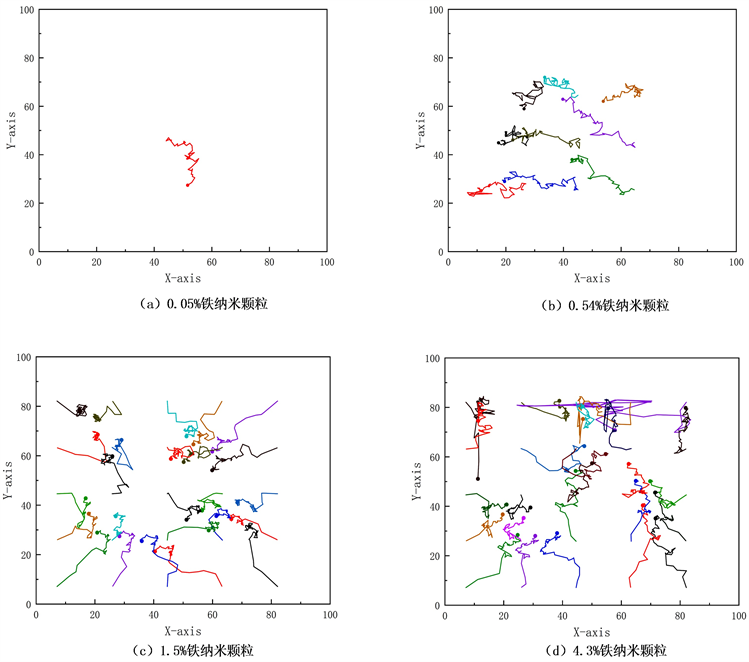
Figure 5. Brownian motion of iron nanoparticles in aqueous medium at 300 k temperature and in the XY plane of nanofluids with different volume fractions (Fe-H₂O) for 500 ps

图5. 300 k温度下，不同体积分数的纳米流体(Fe-H₂O)在XY平面下，500 ps时间段内，铁纳米颗粒在水介质中的布朗运动轨迹

图6呈现300 k温度下，不同体积分数的铁纳米流体中铁纳米颗粒的速度与时间的关系图，计算每10 ps铁纳米颗粒的速度变化。根据图中速度变化，在初始铁纳米颗粒速度为0时，0.05%体积分数的铁纳米流体中单个铁纳米颗粒在纯水介质中无序运动，并保持相对稳定的速度。0.54%、1.5%、4.3%体积分数的铁纳米流体中多个铁纳米颗粒的速度变化，以其中一个铁纳米颗粒为例，该颗粒会因为受到周围多颗铁纳米颗粒的分子间相互作用力和水分子对铁纳米颗粒的相互作用，致使铁纳米颗粒的速度增大，当颗粒与颗粒形成团聚后，其速度逐渐趋于平稳，并且铁纳米颗粒形成团聚的速度和0.05%体积分数的单个铁纳米颗粒的速度一致。图7显示在模拟体系中，铁纳米流体弛豫600 ps后，采用Muller-Plathe算法计算纳米流体(Fe-H₂O)的粘度随铁纳米颗粒体积分数的变化曲线。

由于计算机算力受限，故模拟体系采用的铁纳米颗粒粒径大小为1 nm，实际情况下，此尺寸的纳米颗粒并无法生产，该模拟运用分子动力学对磁性纳米流体的纳米尺度机制进行定性分析，模拟精度无法实际验证。

Figure 6. Particle velocity of nanofluids (Fe-H₂O) with different volume fractions

图6. 不同体积分数的纳米流体(Fe-H₂O)颗粒速度

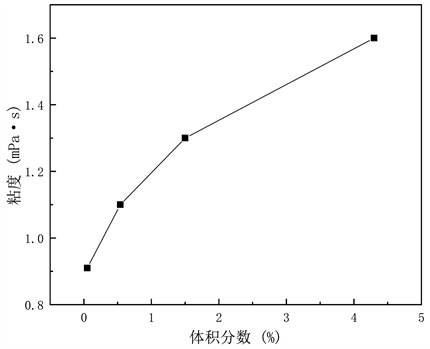
Figure 7. Shear viscosity of nanofluids (Fe-H₂O) with different volume fractions at 300 k

图7. 300 k下不同体积分数的纳米流体(Fe-H₂O)剪切粘度

4. 结论

在本研究中，考察了纳米机制(如布朗运动和铁纳米颗粒团聚)对纳米流体(Fe-H₂O)剪切粘度增强的贡献。通过计算分散的铁纳米颗粒的平均中心速度，并且使用Muller-Plathe算法计算在300k温度下，0.05%、0.54%、1.5%和4.3%的不同铁纳米颗粒体积分数的剪切粘度，定性分析了磁性纳米流体的剪切粘度和铁纳米颗粒体积分数的关系。该数值研究的结果表明，纳米流体(Fe-H₂O)的剪切粘度随着铁纳米颗粒体积分数的增大而增大。因为随着铁纳米颗粒体积分数的增大导致铁纳米颗粒形成团聚对其周围水分子的作用力增大，进而影响纳米流体(Fe-H₂O)的粘度。此外，铁纳米颗粒的速度会随团聚的形成而逐渐趋于平稳。