1. 引言
反散射问题是数学物理反问题领域中的重要课题,其在医学成像、地质探测、无损探伤等领域都有广泛的应用。这种反散射问题通常是指根据波场的散射特性来确定散射体的几何或物理信息。研究障碍反散射问题的一个难点是解的不唯一性,为此需要对该问题施加额外的约束条件。Alessandrini和Rondi [1] ,Liu和Zou [2] 分别证明在单个入射平面波和多个入射平面波情况下利用远场数据来重构声软多面体障碍物的唯一性。目前,求解该类反散射问题的方法主要分为定性法 [3] [4] 和定量法 [5] [6] 。对于定性法而言,其计算速度较快但一般无法精确地反演散射障碍物。对于定量法而言,其虽能够较为精确地反演散射障碍物但需要大量有关障碍物的先验信息且计算量比较大。此外,对于障碍反散射问题,在实际应用中经常存在数据信息缺失的情况。
神经网络模型对非线性映射的拟合效果较好,且能够弥补一定程度上的信息缺失 [7] ,这使得其被广泛地应用于各类非线性问题。反散射问题是一种典型的非线性问题,其可以表述为求解将输入数据和输出数据联系起来的非线性映射。该非线性映射通常由复杂的物理系统所定义,且输入数据和输出数据分别为探测数据和观测数据。Khoo和Ying [8] 建立了一种新的神经网络SwitchNet,通过提供散射体和散射场之间的映射,来解决基于波动方程的反散射问题。Li等 [9] 从神经网络的角度提出了生成几何体的反散射方法,数值实验说明此神经网络方法可以很好地重构几何体的边界。Gao和Zhang [10] 提出了一种基于卷积神经网络的反散射问题的求解方法,并通过数值实验说明该方法能够有效解决基于不完全远场数据的重构问题。更多相关研究可参阅文献 [11] [12] [13] 。
本论文在上述研究的基础上,提出一种基于门控思想的循环神经网络模型,用于求解基于远场数据的障碍反散射问题. 本文的创新之处在于将门控思想结合到循环神经网络中,对远场数据中有关障碍物的特征信息进行保存和更新,以精确地反演散射障碍物。
2. 障碍散射问题
对于在均匀介质中具有声软边界
的不可穿透障碍物
。时谐平面声波
为入射波,其中,
为虚数单位,
为波数,
为单位入射方向。
为入射波频率,c为波速。入射场
和障碍物D相作用生成散射场
,该物理过程满足Helmholtz系统:
其中,
为总场。
为Dirichlet边界条件,这取决于障碍物边界的物理特征。
此外,障碍物D外部的散射场
在无穷远处有如下的渐进形式:
(1)
其中,
为远场模式。(1)在所有的观测方向
上均成立。
散射场中远场模式的物理意义是散射波的振幅。因此,本文采用积分方程法和(1)来计算障碍物D的远场数据
。我们所考虑的障碍反散射问题是指利用远场数据
来重构障碍物D的边界形状。
3. 反演散射障碍的循环神经网络模型构建
本文从神经网络的角度考虑基于远场数据的障碍物重构形状问题。首先给出以下假设:
假设1:入射方向
,观测方向
,入射角度
和观测角度
均匀分布于
:
,
其中,n为入射方向的个数,
为观测方向的个数。
假设2:对于n个入射方向和
个观测方向,当入射角
时,远场数据表示为
;当入射角
,远场数据表示为
;
;当入射角为
,远场数据表示为
,因此,全部的远场数据可表示为
。
假设3:障碍物D的边界曲线
可表示为参数方程
,
,可将
和
表示为如下的参数方程:
其中,
。
为Fourier系数
的有序集合
。
因此,我们所考虑的障碍反散射问题可转化为利用远场数据X来反演障碍物的形状参数Y。
3.1. 构建网络模型
图1中
,
,为t时刻输入的障碍物的远场数据,
,
,为t时刻网络模型的隐藏层状态向量,
,
为t时刻的输出向量,即t时刻网络模型预测的障碍物的形状参数。图1中每个时刻的结构可解释为一个运算单元,每个运算单元主要分为输入层,隐藏层和输出层。该网络模型的隐藏层之间存在连接,这表示其隐藏层的状态值不仅取决于当前时刻的输入数据
,还取决于前一时刻隐藏层的状态向量
。隐藏层和输出层之间是全连接层。
图1中网络模型隐藏层的计算表达式为
其中,
为t时刻隐藏层的状态向量,
为t时刻输入数据,
为t时刻隐藏层单元的更新门。
,
,
,
,
。
为双曲正切函数,
为Hadamard乘积。
更新门
的输出值是位于0和1之间的,用于控制信息通过的多少。当门控值为0时,表示没有信息通过,当门控值为1时,则表示所有信息都可以通过。
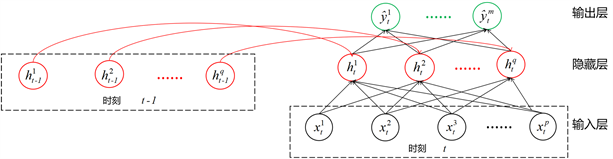
Figure 1. Diagram of the recurrent neural network model of the shape reconstruction of obstacles
图1. 障碍物形状重构的循环神经网络模型图
其中,
,
,
,
为sigmoid函数。
图1中网络模型的输出层的计算表达式为
其中,
,
。
最后,本文经过T个时间步长,可反演出障碍物的形状参数。
3.2. 网络模型参数更新方法
本文考虑使用均方误差作为图1中网络模型的损失函数,并使用Adam优化算法更新权重和偏置。
定义1:令Y为模型的真实输出,
为模型的预测输出,定义损失函数为
其中,m为障碍物形状参数的个数。
利用W表示模型中的权重
,
,
,
,
,
,用b表示模型中的偏置
,
,
,
。本文利用正态分布初始化权重
和偏置
,然后利用Adam优化算法更新权重
和偏置
,
,为网络模型的迭代次数。下面以权重更新为例:
,
,
,
其中,
为损失函数关于权重的梯度矩阵,
和
分别为
的一阶和二阶有偏矩估计,且
和
为零向量,
为矩估计的指数衰减速率,
和
为修正的一阶和二阶矩估计,
为学习率,
为数值稳定常数。此外,在网络模型训练时,我们设置
,
,
,
。
4. 数值实验
实验设置
本文将远场数据和截断的障碍物边界曲线方程的傅里叶系数组成的数据集
作为网络模型的训练数据,并将其按照9:1的比例分为训练集和测试集。表1为网络模型反演障碍物形状参数时的超参数的设置,相关参数选取是参考大量的数值实验和文献 [11] [12] 。

Table 1. The hyper parameter setting of network model
表1. 网络模型的超参数设置
实验1:单个入射方向,多个观测方向,无噪声的远场数据
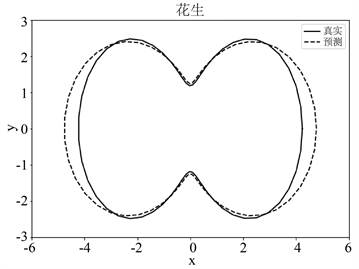
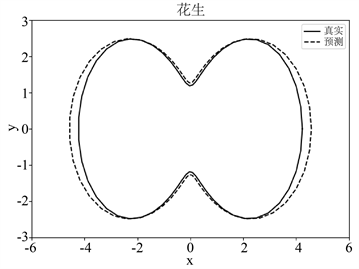
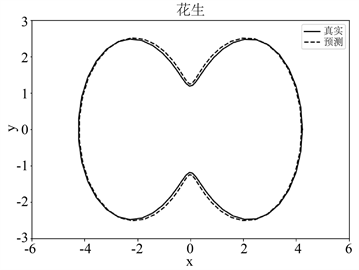
本实验考虑在波数为1.5的单个入射方向的时谐平面声波,15,25,35个观测方向情况下的花生形状和风筝形状障碍物的远场数据和形状参数分别作为网络模型的训练数据。接下来,我们分析网络模型在不同观测方向个数下对障碍物的重构效果。
(a)
(b)
(c)
Figure 2. Diagram of reconstruction effects of peanut-shape obstacles with
, respectively
图2.
分别为15,25,35下花生形状障碍物重构效果图
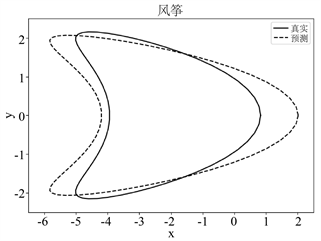
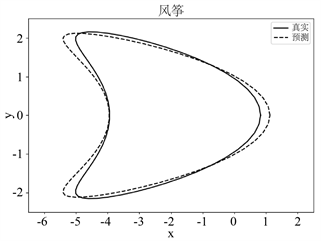
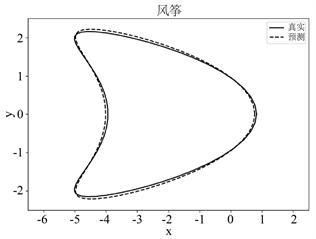
由图2中的(a)~(c)可知,当入射方向的个数固定时,随着观测点个数的增加,该网络模型重构花生形障碍物的效果逐渐变好。这是由于观测方向个数的增加会使得远场数据中障碍物的特征信息增加,从而使得障碍物的重构效果逐渐变好。当观测方向的个数增加到35时,该网络模型能够较为精确地重构障碍物的形状。根据图3中的(a)~(c),对于风筝形状的障碍物,可以得出类似的重构效果。此外,图4中的(a)和(b)说明该网络模型在35个观测方向下对两种形状障碍物的重构损失较小,并说明其具有收敛性。
(a)
(b)
(c)
Figure 3. Diagram of reconstruction effects of kite-shape obstacles with
, respectively
图3.
分别为15,25,35下风筝形状障碍物重构效果图
 (a) 花生损失值
(a) 花生损失值 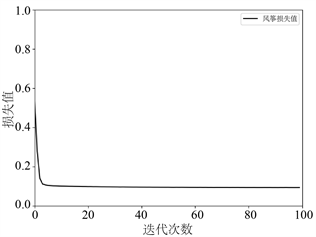 (b) 风筝损失值
(b) 风筝损失值
Figure 4. Diagram of reconstruction losses of two shapes of obstacles with
observation directions
图4. 在35个观测方向下两种形状障碍物的重构损失图
实验2:单个入射方向,多个观测方向,有噪声的远场数据
在实际测量中,远场数据通常含有测量误差,即噪声数据。由实验1可知,在单个入射方向,35个观测方向时,该网络模型能够较为精确地重构障碍物的形状。因此,在实验1参数设置的基础上,本实验分别在远场数据中添加5%,10%和20%高斯白噪声。下面我们分析该网络模型在不同噪声水平下对障碍物的重构效果。
 (a) 数据集加5%噪声
(a) 数据集加5%噪声 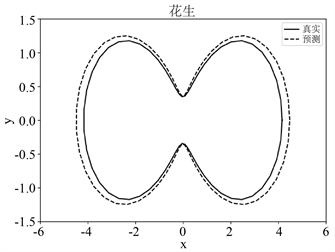 (b) 数据集加10%噪声
(b) 数据集加10%噪声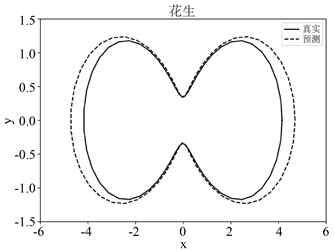 (c) 数据集加20%噪声
(c) 数据集加20%噪声
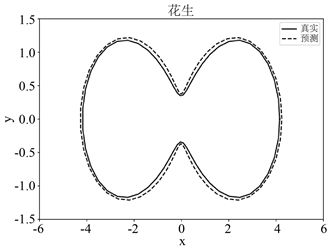
Figure 5. Diagram of reconstruction effects of peanut-shape obstacles with noisy far-field data
图5. 噪声远场数据下花生形状障碍物重构效果图
 (a) 数据集加5%噪声
(a) 数据集加5%噪声 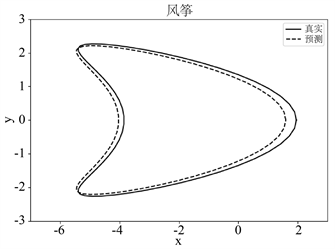 (b) 数据集加10%噪声
(b) 数据集加10%噪声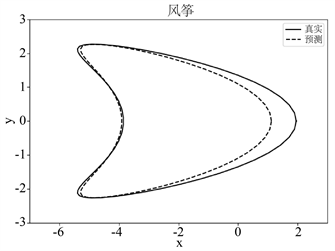 (c) 数据集加20%噪声
(c) 数据集加20%噪声
Figure 6. Diagram of reconstruction effects of kite-shape obstacles with noisy far-field data
图6. 噪声远场数据下风筝形状障碍物重构效果图
 (a) 花生损失值
(a) 花生损失值  (b) 风筝损失值
(b) 风筝损失值
Figure 7. Diagram of reconstruction losses of two shapes of obstacles with 5% noise levels
图7. 在5%噪声水平下两种形状障碍物的重构损失图
由图5中的(a)~(c)可知,随着远场数据中高斯白噪声水平的增加,该网络模型对花生形障碍物的重构效果逐渐变差。这是由于噪声水平的增加会导致远场数据损失有关障碍物的特征信息,从而影响障碍物形状重构的效果。根据图6中的(a)~(c),对于风筝形障碍物的重构效果也是在逐渐变差。本文发现当噪声水平较低时,该网络模型重构障碍物形状的效果是可以接受的。此外,图7中的(a)和(b)表明该网络模型在5%噪声水平下对两种形状障碍物的重构损失较小,并说明其具有收敛性。
5. 总结
本文建立了一种反演散射障碍的循环神经网络模型,该模型以门控思想为基础。在训练网络模型时,选择均方误差和Adam优化算法来进行网络模型参数的更新。数值实验表明该网络模型能够较好地重构障碍物形状,即使在远场数据含有少量噪声干扰的情况下,其仍能较好地反演障碍物形状。
NOTES
*通讯作者。