基于近场动力学的齿根裂纹扩展特性研究

Research on Crack Growth Characteristics of Dedendum Based on Peridynamics

摘要: 为优化齿根裂纹扩展问题的分析，在标准渐开线齿轮对上，基于近场动力学理论建立齿轮接触啮合断裂模型，模拟近场动力学下齿轮齿根断裂啮合过程。近场动力学理论通过空间积分的方法，避免了传统有限元在分析裂纹尖端问题时的奇异性。首先建立一对健康的渐开线齿轮模型并通过近场动力学接触理论确定齿根在啮合过程中应力最大点，从而确定裂纹起始点并预制裂纹；通过近场动力学方法可以有效避免裂纹扩展过程中不断重新划分网格的问题。然后通过基于节点位移的应力强度因子反推法得到裂纹扩展后的应力强度因子。最后依据Paris公式对齿根疲劳裂纹剩余寿命进行评估。从近场动力学裂纹扩展结果上看，近场动力学方法下裂纹扩展方向、疲劳周期与有限元中结果是一致的。该研究结果可以提供一种新的方法进行齿轮接触疲劳分析。

Abstract: In order to optimize the analysis of tooth root crack propagation problem, a gear contact meshing fracture model was established based on the peridynamicstheory on the standard involute gear pair, and the meshing process of tooth root fracture was simulated under the peridynamics. The peridynamics theory avoids the singularity of the traditional finite element method in analyzing the crack tip problem by using the method of space integration. Firstly, a pair of healthy involute gear models was established and the maximum stress point of tooth root during meshing was deter-mined by the peridynamics contact theory. Then the crack initiation point was determined and the crack was prefabricated. The peridynamics method can effectively avoid the problem of constantly remeshing during crack propagation. Then, the stress intensity factor after crack propagation is obtained by the inverse stress intensity factor method based on node displacement. Finally, the re-sidual life of root fatigue crack was evaluated according to Paris formula. According to the results of peridynamics crack propagation, the direction of crack propagation and fatigue period under the peridynamics method are consistent with those obtained in the finite element method. The re-search results can provide a new method for gear contact fatigue analysis.

1. 引言

齿轮传动是机械结构部件最常见传动行式之一，同时齿轮传动具有高效率、结构紧凑与可靠度高等特点而广泛应用于各种机械部件中。据统计，齿根疲劳断裂是影响齿轮传动失效的主要原因之一，在经典连续介质理论中，裂纹尖端存在奇异性，同时与一些裂纹扩展理论分析问题时，需要不断重新划分网格。研究齿轮啮合断裂问题关键是设定好接触条件与进行齿根断裂分析。

在连续介质力学中，通过赫兹接触模型和裂纹表面接触模型去描述接触行为，但是这种方式只能应用于一些理想情况。Dolbow等 [1] 使用了X-FEM方法，并通过大时间迭代格式增量方法模拟任意演化界面上的摩擦接触。冲击和侵彻接触模拟可以使用光滑例子和材料点法，但是需要进一步研究与接触相关的材料断裂行为。近场动力学(PD) [2] 是Silling在2000年提出的用于分析不连续问题的连续力学的一种非局部粒子方法。在PD理论中，不需要空间导数，用积分方程取代连续力学中的偏微方程，可以有效的避免裂纹尖端奇异性的问题。因此，PD模型可以很自然地应用于裂纹萌生、扩展和路径选择等不连续问题，且不需要额外的理论支持。经过多年的发展，PD可分为三种 [3] 类型，即基于键的近场动力学(BB-PD)、基于普通状态的近场动力学(OSB-PD)和基于非普通状态的近场动力学(NOSB-PD)取决于物质点之间的相互作用。同时，近场动力学中各种键合破坏模型被提出用于定量分析断裂，如基于临界拉伸准则、基于临界能量密度准则、混合模式键合破坏准则以及强度和能量耦合破坏模型。此外，经典断裂力学方法也在近动力理论的框架下得到了重新阐述，如虚拟裂纹闭合技术 [4] 与J积分 [5]。

本文通过建立近场动力学齿轮接触模型，为了得到齿根裂纹尖端的应力强度因子，首先分析健康齿轮在啮合过程中的齿根处的应力情况，确定最大应力节点，同时将该点作为裂纹起始点 [6]。在近场动力学理论下，划分齿轮网格，确定其相互作用下的近场域。通过节点位移反推法得出裂纹尖端的应力强度因子。根据Paris公式得到裂纹扩展直至失稳后的循环状况 [7] [8]。

本文通过近场动力学理论与Paris理论进行齿轮齿根裂纹扩展分析，通过PD方法可以自动确定裂纹扩展方向，提出一种新的方式去解决齿轮啮合接触问题，避免裂纹尖端奇异性问题，同时不需要重复性的划分网格，为齿根断裂分析提供新的方法。

2. 近场动力学理论

2.1. 近场动力学理论

近场动力学理论是固体力学标准数学理论的扩展，它与裂纹的不连续性质相容。标准理论的偏微分方程不能直接应用于不断增长的裂纹，与之相比，近场动力学理论使用的是不涉及变形的空间导数的积分–微分方程。

近场动力学力学方程：

$\begin{array}{l}\rho \left(x\right)\ddot{u}\left(x,t\right)={\displaystyle \underset{H}{\int }f\left(x^{\prime },x,t\right)\text{d}{V}_{x^{\prime }}}+b\left(x,t\right)\\ \forall x\in \beta ,t\ge 0\end{array}$ (1)

式中， $u$ 为物质节点的位移，x为物体B参考构型中的物质点， $\rho$ 为密度场，b为规定的外力密度。球面邻域 $H_x\subset B$ 以x为中心，但不包括x，称为x的族：

$H_x=\left\{x^{\prime }\in \beta |0<\left|x^{\prime }-x\right|<\delta \right\}$ (2)

邻域 的半径称为近场域，它可以是有限的，也可以是无限的，可以被认为是一种物质属性。向量场 $f$ 为键的力密度，键的力密度与材料本构模型的变形量有关。

物质点之间的相对位置键的定义：

$\xi =x^{\prime }-x,x^{\prime }\in H_x$ (3)

其被称为键，键的示意图如图1所示。近场动力学理论中的本构模型规定了每个键中的成对力密度 $f$ 。这个成对的力密度由两部分组成，由作用在 $x$ 和 $x^{\prime }$ 处的本构模型确定：

$f\left(x^{\prime },x,t\right)=t\left(x^{\prime },x,t\right)-t\left(x,x^{\prime },t\right)$ (4)

其中，右边的两项分别包含了 $H_x$ 和 $H_{x^{\prime }}$ 的力密度。 $H_x$ 变形的力密度：

$t\left(x^{\prime },x,t\right)=\underset{\_}{T}\left[x\right]\langle \xi \rangle$ (5)

其中 $\underset{\_}{T}\left[x\right]$ 是一个函数，称为x处的力矢量状态，它将任何键 $x^{\prime }-x$ 映射到键中相应的力密度向量。力矢量状态是一个近场动力状态的一个例子，它只是一个定义在一个族上的函数。

对应的态型近场动力学力学方程为：

Figure 1. Diagram of “bond”

图1. “键”示意图

$\rho \left(x\right)\ddot{u}\left(x,t\right)={\displaystyle \underset{H}{\int }\left[\underset{\_}{T}\left(x,t\right)\langle \xi \rangle -\underset{\_}{T}\left(x^{\prime },t\right)\langle -\xi \rangle \right]\text{d}{V}_{x^{\prime }}}+b\left(x,t\right)$ (6)

2.2. PD模型离散化

本文使用Peridigm开源软件进行PD程序的计算，在PD建模的过程中，将材料离散成排列有序的球体，每一个球体代表一个物质点，同时将其称为单元节点，节点间的间距为Δx，从而得到无网格的近场动力学模型。如图2所示，是一个近场域以3.015Δx为半径的近场动力学二维图。

Figure 2. The horizon in PD mode

图2. PD模型离散近场域

2.3. Paris 扩展理论

疲劳裂纹扩展一般分为三个阶段。

第一阶段：裂纹萌生阶段。

第二阶段：裂纹稳定扩展阶段。利用Paris公式可以计算循环周期即剩余寿命。Paris公式如下

$\frac{\text{d}a}{\text{d}N}=C{\left(\Delta K\right)}^m$ (7)

其中，a为裂纹的扩展长度，N为循环次数，ΔK为应力强度因子变化幅，C和m为与材料有关的常数。

第三阶段：裂纹失稳扩展阶段。零部件会在极短时间内疲劳折断。

3. 齿轮啮合的PD接触模型

本节主要介绍PD接触理论与齿轮接触啮合过程中齿轮齿根应力最大的位置，同时将其作为疲劳裂纹的起点。

3.1. 近场动力学接触理论

两个离散PD模型的接触区域如图3所示。在PD数值模型中，目标和接触器的边界表面从最外层节点沿其向外单位法向量 $n_1$ 和 $n_2$ 扩展 $0.5{\delta }_1$ 和 $0.5{\delta }_2$ 得到的，其中 ${\delta }_1$ 和 ${\delta }_2$ 是近动态目标和接触器体的网格尺寸。由于接触的基本条件是不发生材料重叠，近场动力模型中的接触发生在 [9] ：

$\left(y_i-y_m\right)\cdot n<0.5\left({\delta }_1+{\delta }_2\right)$ (8)

式中， $y_i$ 和 $y_m$ 为边界节点 $x_i$ 和 $x_m$ 的变形向量，其中 $x_i$ 和 $x_m$ 为接触器和目标体的最外层节点， $n$ 为接触面单位法向量。

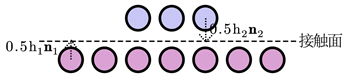
Figure 3. Contact surface in PD model

图3. PD模型下的接触面

在非局部公式接触中，针对两种不同的接触情况，定义PD接触结合力的形成，如图4为滑动接触模型接触键力示意图；当产生滑动摩擦接触时，PD法向接触黏结力和切向接触黏结力分别表示为 [9] ：

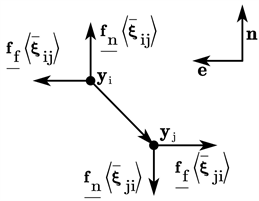
Figure 4. Sliding contact model contact bond force

图4. 滑动接触模型接触键力

$\underset{\_}{f_n}\langle {\bar{\xi }}_{ij}\rangle =-c_n\underset{\_}{s_n}\langle {\bar{\xi }}_{ij}\rangle \underset{\_}{\omega }\langle {\bar{\xi }}_{ij}\rangle n$ (9)

$\underset{\_}{f_f}\langle {\bar{\xi }}_{ij}\rangle =\mu \left|\underset{\_}{f_n}\langle {\bar{\xi }}_{ij}\rangle \right|e$ (10)

式中 $\underset{\_}{s_n}$ 为键的法向拉伸量， $\underset{\_}{\omega }$ 为影响函数，μ为摩擦系数， $n$ 、 $e$ 为接触面单位法向向量和切向向量，其中 $e$ 与滑动方向相反。 $c_s$ 、 $c_n$ 为近场动力接触键粘着和滑动微模量。

滑动摩擦接触时，计算了键合法向拉伸 $s_n$ ，键合变形的切向分量对接触键合力没有贡献。此外，对于滑动情况，接触黏结力受牛顿第三定律约束为：

$\underset{\_}{f}\langle {\bar{\xi }}_{ij}\rangle =-\underset{\_}{f}\langle {\bar{\xi }}_{ij}\rangle$ (11)

3.2. 健康齿轮模型分析

本文以渐开线标准圆柱齿轮为研究对象，使用Peridigm程序进行PD模型中齿轮的仿真计算。Perdiigm是基于C++开发的开源PD程序，在使用Peridigm程序计算PD模型的过程中，需要历经所有节点的计算，所以简化为其部分齿轮二维啮合模型，其参数如表1所示。通过平面应变单元(ABAQUSCPE4I)建立齿轮的有限元模型，然后将生成的inp文件导入到可生成二进制模型软件中重新进行网格的划分以及节点集与块的定义，其中节点单元间距Δx为0.1 mm，则选取近场域半径为0.3015 mm；最后导出生成Peridigm程序可以识别的g文件模型，如图5为PD模型下的齿轮离散模型。

Table 1. Gears parameters

表1. 齿轮参数

Figure 5. PD discrete model

图5. PD离散模型

3.2.1. 载荷加载条件

在Peridigm开源程序中，接触模块是完全打开或是完全关闭的行式，所以定义好两个物块后，设定0.1 mm的接触距离判定条件，他会将两个块中的所有节点进行计算判定。同时通过查阅资料可知，18CrNiMo7-6的齿轮在润滑情况下的摩擦因数范围为0.1~0.15，选择摩擦系数为0.1。

施加的边界条件为给大齿轮25 rad/s的转速，固定小齿轮底部，本文采用Verlet求解分析，初始时间0，结束时间为3.63e-6s，时间增量设定为1e-8s。

3.2.2. 应力分析结果

模拟健康齿轮的啮合过程，从动轮齿根最大应力–啮合位置关系。如图6为近场动力学理论下的齿轮啮合应力云图，可以观察到，除去接触位置外，小齿轮齿根处较大，进一步提取应力最大处的节点编号为141,641，选取该节点周围6个节点分析啮合过程中应力最大的位置。考虑到Peridigm程序无法实现齿轮模型的接触啮合转动，所以将齿轮的啮合过程以定角度分解，从图7中可以看到在第九步的时候应力达到最大值。

4. 齿轮啮合裂纹扩展分析

上述齿轮的材料为18CrNiMo7-6，查阅资料可知，常温情况且零应力比条件下，应力强度因子门槛值 $K_{\Delta th}=3.8\text{MPa}\cdot \sqrt{m}$ ，应力强度因子极限值 $K_{IC}=93.3\text{MPa}\cdot \sqrt{m}$ ，Paris公式中常数c与m分别为 $2.9\times {10}^{-8}$ 与2.3051 [10]。

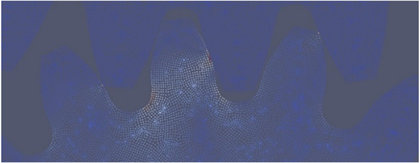
Figure 6. Gear root stress cloud diagram

图6. 齿轮齿根应力云图

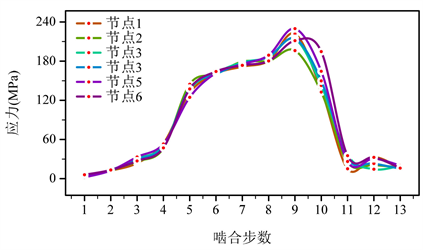
Figure 7. Tooth root stress loading position history diagram

图7. 齿根应力加载位置历程图

4.1. 基于位移分析的应力强度因子

含裂纹的齿轮在啮合过程中，应力强度因子时可以表征其收到损坏的程度，同时利用Paris公式可以求得裂纹长度与循环寿命之间的关系。在齿轮齿根啮合破坏过程中，裂纹以张开型裂纹为主，所以通过张开型应力强度因子的计算来判断齿轮的可靠度。本文通过基于位移节点的外推法去计算应力强度因子。

基于节点的位移外推法需要裂纹周围20个节点的位移，在节点间距为0.1 mm情况下，预制2 mm的初始裂纹。

如图8是裂纹尖端应力强度因子随着扩展步变化图，随着裂纹长度的扩展，应力强度因子先是稳定的增加，此时为稳定扩展阶段，在达到 值后，迅速增大，此时裂纹进入失稳扩展阶段。

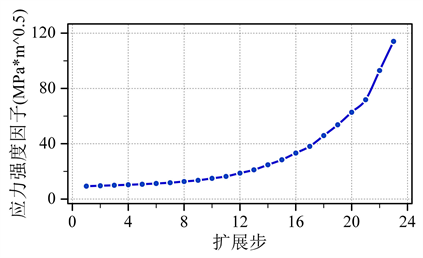
Figure 8. Crack tip stress intensity factor propagation step change

图8. 裂纹尖端应力强度因子扩展步变化

4.2. pd齿根疲劳寿命分析

依据Paris公式保守估计裂纹扩展次数，如图所示。图中明显可以看出，在裂纹扩展初期，循环次数为最大，随着裂纹的扩展，循环次数，明显减少。利用PD方法处理齿根裂纹扩展问题符合齿根裂纹扩展的实际过程。

又由图9可知，齿轮共进行了35.8 × 10⁴次循环。

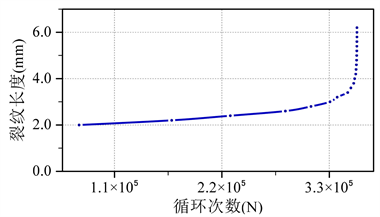
Figure 9. Relationship between crack length and cycle times

图9. 裂纹长度与循环次数关系

4.3. 近场动力学下裂纹扩展路径

如图10是基于PD方法生成的裂纹路径，该路径通过设定“键”的临界伸长量，在预制初始裂纹后，通过的载荷加载，节点之间的“键”发生断裂，产生PD模型下的裂纹路径。

Figure 10. Crack path map based on PD method

图10. 基于PD方法的裂纹路径图

与文 [6] 对比裂纹扩展路径，同每一步进行裂纹方向判断不同，PD模型可以自发形成裂纹的扩展，同时裂纹扩展的方向同文 [6] 中相似，疲劳裂纹都是从齿根一边向对面侧进行扩展。PD模型下的齿轮扩展结果满足实际工程的需要，提供了一个新的方法去检测齿轮齿根的健康状况。

5. 结论

基于齿轮齿根裂纹扩展特性研究可知，本文的主要特点为：

结合近场动力接触理论，模拟出齿轮在啮合过程，确定齿根在啮合过程中最大应力的位置，并将2 mm的初始裂纹预制在该位置；通过近场动力学与基于位移外推法应力强度因子的计算，结合Paris公式确定了裂纹扩展周期，模拟了裂纹扩展路径，预测出疲劳裂纹的剩余寿命。对比与有限元结果，近场动力学方法是可以有效进行齿根裂纹扩展的模拟；近场动力学理论基于积分位移的模型避免裂纹尖端奇异性的问题，在裂纹扩展过程中，不需要重复性的进行网格的划分。