一维准晶体紧束缚模型的高度函数和波函数的多分形性

Height Function of a 1D Tight-Binding Quasicrystal Model and Multifractality of Wavefunction

摘要: 在一维准晶体模型上构造了紧束缚哈密顿量，并且根据替代规则研究了中心电子态。通过计算高度函数的分布，得到了波函数的多分形谱。结果显示出临界态的典型性质。

Abstract: A tight-binding Hamiltonian is constructed in a one-dimensional quasicrystal model and the central electronic eigenstate is investigated based on the substitution rule. By computing the height function distribution, the multifractal spectrum of the wavefunction is obtained. The results show typical behaviors of the critical state.

1. 引言

自从准晶体首次在实验制备出的金属合金中发现以来，其电子性质一直引起人们的普遍兴趣。准晶体可具有5次或6次以上的旋转对称性，由此带来了与周期晶体很不同的结构和物理性质。然而，这种对称性并不能直接产生一种类似晶体能带理论的解析方法来计算能谱，因此多数研究都借助于数值模拟。除了一维情况下的一些例子外，准晶体的电子态还没有得到很好的表征。

一般认为准晶体的本征态不仅包含扩展态和局域态，而且还有自相似的临界态，相应的能谱是奇异连续谱，具有多分形性质 [1] - [7] 。能谱与准晶体对称性之间的关系并不明显，因此对特定模型的数值计算往往更有效。但对于一维准晶体来说，利用其简单的替代规则可以对能谱甚至波函数进行解析计算。Fibonacci链作为一维准晶体的标准模型，在过去的几十年里得到了广泛的研究 [8] [9] [10] [11] [12] 。其研究意义在于，一维Fibonacci链是一个与三维二十面体准晶体密切相关的准周期点阵。因此，对准晶体的电子性质的研究很自然地从一维Fibonacci链的本征态的研究开始，其电子能谱和波函数的多分形特征最能体现出原子结构中的准周期序。

虽然人们对一维准晶体模型的能谱性质已有相当深入的研究，但对波函数的表征还相对较少，其主要原因是不能对所有波函数的多分形性质进行解析计算。最近的一些工作给出了准晶体中的多分形态的精确解，特别是对于一维Fibonacci模型的E = 0中心态 [13] [14] [15] [16] 。但是到目前为止，对于一维Fibonacci链以外的其他准晶格还没有深入的解决方案。鉴于准晶体的电子态对理解准晶主要物理性质的重要性，研究各类一维准晶体中的本征态是非常必要的。本文将给出一种广义Fibonacci准晶模型波函数性质的具体计算和分析方法，研究其临界态的多分形特征。该方法将波函数的解用高度函数表达，相比于之前单纯的数值计算法，可得到意义较为明确的解析解。而且由于高度函数通过简单的替换规则即可得到，准晶模型的物理性质与准晶格结构的关系能更为直接地反映出来。

2. 模型和电子能谱

本文研究的一维准晶模型是所谓的广义Fibonacci准周期模型，首先由Gumbs和Ali [17] 提出，然后其他研究者对此也开展了很多的工作 [18] [19] [20] [21] [22] 。通过替代规则，可以产生一个广义Fibonacci链：

$a\to a^m{b}^n,b\to a.$ (1)

其中m和n是整数，a^m代表总数为m的字母a的序列，bⁿ代表总数为n的字母b的序列。最初的Fibonacci链是由m = 1和n = 1的替换规则产生的。

关于准晶体的电子性质的研究，采用如下形式的紧束缚哈密顿量：

$H=\underset{i}{{{\displaystyle \sum }}^{\text{}}}|i\rangle {\epsilon }_i\langle i|+\underset{i}{{{\displaystyle \sum }}^{\text{}}}\left(|i-1\rangle t_{i-1}\langle i|+|i\rangle t_i\langle i+1|\right).$ (2)

其中， ${\epsilon }_i$ 为第i个格点的座能量，t_i为格点i和i + 1之间的跳跃积分振幅。在理论模型中，假设这些参数仅由每个格点的最近邻决定。我们考虑哈密顿量(2)的迁移模型，其中格点座能量设置为常数，即 ${\epsilon }_i=0$ ，跳跃积分振幅根据替换规则(1)生成的序列取两个值t_a和t_b中的一个。此模型也被称为非对角模型，因为在哈密顿量中非对角元素呈准周期阵列。下面我们研究m = 2和n = 3的广义Fibonacci链，将其称之为GF(2, 3)准周期模型。从ab开始，反复使用替换，产生越来越长的准周期序列。如果取aabbba为第一代，则第二代为aabbbaabbbaaaaabbb。第三代由54个元素组成，其顺序如下：

$aabbbaabbbaaaaabbbaabbbaaaaabbbaabbbaabbbaabbbaabbbaaa.$ (3)

在这里，每一对字母都加下划线，以便在后续的研究中分析箭头函数。

在一个包含N个元素的链中，有N个键和N + 1个格点。第(i + 1)个格点通过左侧的键t_i连接到第i个格点，通过右侧的键t_{i + 1}连接到第(i + 2)个格点。具有 ${\epsilon }_i=0$ 和t_i = t_a或t_b的哈密顿量(2)的本征方程可化为：

$t_i{\psi }_i+t_{i+1}{\psi }_{i+2}=E{\psi }_{i+1},i=1,2,\cdots ,N-1.$ (4)

能谱可以通过数值对角化来计算。图1为第七代GF(2, 3)链的积分态密度(idos)，由1093个格点组成，其中t_a = 0.5和t_b = 1。积分态密度曲线有许多“魔鬼阶梯”，呈自相似的分形结构，这是一维准晶体的典型特征 [22] [23] [24] [25] [26] 。

3. 高度函数和膨胀矩阵

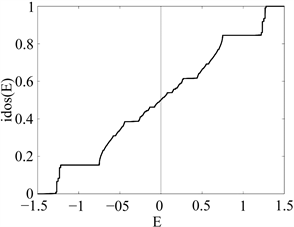
Figure 1. The integrated density of states of the GF(2, 3) quasilattice of the seventh generation with total number of site N = 1093 and hopping integrals t_a = 0.5 and t_b = 1

图1. 第七代GF(2, 3)准晶格的态积分密度，格点总数为N = 1093和跳跃积分振幅为t_a = 0.5和t_b = 1

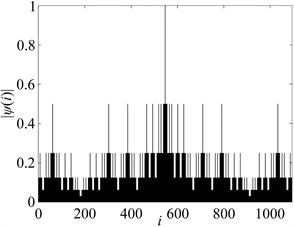
Figure 2. The wavefunction of the eigenstate with E = 0 for a GF(2, 3) quasilattice of the seventh generation with total number of site N = 1093 and hopping integrals t_a = 0.5 and t_b = 1

图2. 第七代准格点GF(2, 3)的E = 0时的波函数本征态，格点总数N = 1093和跳跃积分振幅为t_a = 0.5和t_b = 1

从替换规则(1)中可以明显地看出，能谱关于E = 0对称，图1中的数值计算证实了这一点。如果格点总数N为奇数，则中心能量E = 0是N个特征值之一，这个中心态有其特殊的性质，是我们重点研究的对象。我们通过数值方法计算了中心态的波函数，如图2所示。参照文献 [14] [16] 中提出的方法，对中心态是有可能进行解析研究的。

对于有限个格点组成的准周期链，将E = 0的中心态的方程(4)简化为一个简单的迭代形式：

${\psi }_{i+2}=-\frac{t_i}{t_{i+1}}{\psi }_i.$ (5)

对于奇数格点上的波函数振幅，通过ψ₁可求得ψ_{2k + 1}的值，其中整数k > 0：

${\psi }_{2k+1}={\left(-1\right)}^k\underset{j=1}{\overset{k}{{\displaystyle \prod }}}\frac{t_{2j-1}}{t_{2j}}{\psi }_1.$ (6)

同样的，对于偶数格点上的波函数振幅，可以通过ψ₂求得ψ_2k，其中整数k > 1：

${\psi }_{2k}={\left(-1\right)}^k\underset{j=1}{\overset{k}{{\displaystyle \prod }}}\frac{t_{2j}}{t_{2j+1}}{\psi }_2.$ (7)

方程式(6)中奇数点上的波函数振幅和方程式(7)中偶数点上的波函数振幅的递归关系是独立的。下面我们将研究奇数格点的子晶格上的波函数振幅。

定义跳跃积分比ρ = t_a/t_b，则(6)中的两个键t_{2j − 1}/t_2j之间的比值只取三个值ρ、1和1/ρ，这取决于两个相邻的键。因此，方程式(7)中得到的结果一定是ρ的幂函数。为了便于波函数的计算，引入箭头函数A(t_i, t_{i + 1}) [14] ，由元素a和b的四种排列产生三个值：

$A\left(ab\right)=+1,A\left(ba\right)=-1,A\left(aa\right)=0,A\left(bb\right)=0.$ (8)

为了得到波函数的显式表达式，在子晶格的奇格点上引入了高度函数h(m)，其中 $m=1,3,5,\cdots$ 。高度函数是箭头函数从第一个格点到第m个格点的累加，其中m = 2k + 1 ( $k=1,2,3,\cdots$ )：

$h\left(2k+1\right)={\displaystyle \underset{j=1}{\overset{k}{\sum }}A}\left(t_{2j-1},t_{2j}\right)\text{.}$ (9)

将高度函数代入方程(6)，利用ρ = t_a/t_b，得到了波函数迭代的表达式：

${\psi }_{2k+1}={\left(-1\right)}^k{\rho }^{h\left(2k+1\right)}{\psi }_1.$ (10)

Figure 3. The height function of GF(2, 3) quasilattice on the even sites of the seventh generation with total number of site N = 1093

图3. 第七代GF(2, 3)准晶格在偶数个格点上的高度函数，总格点数量为N = 1093

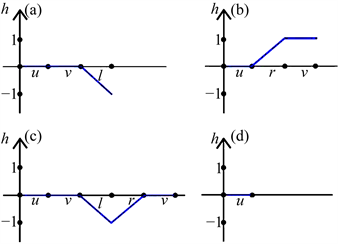
Figure 4. Four cases of the height change after a substitution of an arrow. The original arrows are (a) r, (b) l, (c) u, and (d) v, respectively; each substitution flips the sign of the height value between +1 and −1, or keeps unchanged for the height value 0

图4. 四种高度变化后箭头的位置。原始的箭头是(a) r，(b) l，(c) u，和(d) v；每次替换都会产生翻转的符号为1和−1之间的高度值，或保持不变的高度值0

结果表明，对波函数的计算将被转换为计算高度函数。对只有有限个格点的GF(2, 3)准晶格，高度函数如图3所示，计算的总格点数为N = 1093，其取值h(m)在[−3, 2]的范围内波动。从图3中可以看出高度函数与图2的波函数是相对应的，拥有相同的自相似性质。通过有限长序列的高度函数可以初步判断无限长准周期序列上电子波函数的局域性。

为了表征高度函数，我们在GF(2, 3)准晶格上定义四个箭头符号，它们对应于方程式(8)中的箭头值。分别为r = ab，l = ba，u = aa和v = bb，这可以在序列(3)中看到。对上述四对字母应用替换规则(1)，可生成箭头符号的膨胀规则：

$r\to uvl,l\to urv,u\to uvlrv,v\to u.$ (11)

从(11)可以观察到，箭头r和l的高度在一次膨胀后发生了翻转，而箭头u和v的高度保持为0，如图4所示。例如，在图4(a)中，膨胀的净高度 $r\to uvl$ 为l，即高度从+1变为−1。箭头膨胀(11)过程中高度的转换可以用膨胀矩阵很好地描述。

$M\left(-1\right)=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],M\left(0\right)=\left[\begin{array}{cccc}0& 1& 0& 0\\ 1& 0& 1& 0\\ 1& 1& 1& 1\\ 1& 0& 2& 0\end{array}\right],M\left(1\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right].$ (12)

上述矩阵可用于计算准晶格替换下箭头的膨胀次数。用 $\left(n_r,n_l,n_u,n_v\right)$ 表示在某一GF(2, 3)链上格点前面有箭头 $\left(r,l,u,v\right)$ 的格点数量。在替换时，这些数量将变为 $\left({n^{\prime }}_r,{n^{\prime }}_l,{n^{\prime }}_u,{n^{\prime }}_v\right)$ ，它与前面的 ${\left({n^{\prime }}_r,{n^{\prime }}_l,{n^{\prime }}_u,{n^{\prime }}_v\right)}^{\text{T}}=P{\left(n_r,n_l,n_u,n_v\right)}^{\text{T}}$ 有关，其中变换矩阵P为：

$P=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 1& 0\\ 1& 1& 1& 1\\ 1& 1& 2& 0\end{array}\right]$ (13)

矩阵(12)和(13)也提供了一种格点在不同环境下的高度分布的计算方法 [14] 。对于一个给定的(2, 3)链，设N_μ(h)是在其前面的高度为h和箭头μ (μ = r, l, u, v)的格点数量，它是矢量N(h)的三个组成部分之一。在根据(11)进行膨胀后，矢量变成 [27] ：

$N^{\prime }\left(-h\right)={\displaystyle \underset{h^{\prime }=-1}{\overset{1}{\sum }}M\left(h^{\prime }\right)N}\left(h+h^{\prime }\right).$ (14)

其中M(h')是(12)中给出的矩阵。

4. 多分形性质

根据上述结果，现在分析中心态E = 0的波函数的多分形性质。由波函数矩的标度性质可推导出分形维数 [28] - [33] 。波函数ψ的q次权重定义为：

${\chi }_q\left(\psi ,N\right)=\frac{\underset{i=1}{\stackrel{N}{{{\displaystyle \sum }}^{\text{}}}}{\left|\psi \left(i\right)\right|}^{2q}}{{\left(\underset{i=1}{\stackrel{N}{{{\displaystyle \sum }}^{\text{}}}}{\left|\psi \left(i\right)\right|}^2\right)}^q}.$ (15)

其中，N为一个给定的准周期链中的格点数。χ_q函数是对电子存在概率分布的一种度量。考虑一系列GF(2, 3)的准晶格，由替换产生不同数量的格点，使N增长到无穷大。在准晶格内第q个分形维数d_q(ψ)是q次权重的标度，其定义为：

$d_q\left(\psi \right)=\underset{N\to \infty }{\lim }\frac{-1}{q-1}\frac{\ln {\chi }_q\left(\psi ,N\right)}{\ln N}.$ (16)

然后可以计算分形维数f(α)的Legendre变换。这个函数给出了波函数标度指数为α的格点的比例。标度指数α和分形维数f(α)可以通过以下方程得到 [34] [35] ：

${\alpha }_q=\frac{\text{d}}{\text{d}q}\left(q-1\right)d_q$ 和 $f\left({\alpha }_q\right)=q{\alpha }_q-\left(q-1\right)d_q.$ (17)

根据不同的ρ = t_a/t_b值计算f(α)并绘制曲线，如图5所示。从图中可看出，在每种情况下，α值都在一个有限的范围内，说明波函数是多分形的。当ρ趋于1时，函数曲线收敛于单点α = 1，对应于扩展状态。函数f(α)围绕其最大值对称，通过对波函数的数值计算也验证了这一点。

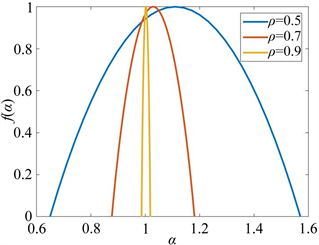
Figure 5. The multifractal spectra for the eigen function of the state with E = 0. Several different values for ρ = t_a/t_b are used

图5. 本征态为E = 0时，本征函数的多重分形谱。其中ρ = t_a/t_b取了几个不同的值

5. 结论

本文研究了一种广义Fibonacci模型GF(2, 3)的电子性质。通过对箭头函数和高度函数的膨胀矩阵的分析，详细研究了中心态的波函数。结果表明，中心态的性质与Fibonacci链相同。通过对积分态密度和波函数的数值计算，以及通过多分形谱，验证了其临界态性质。虽然目前的工作只是在一个特殊的广义Fibonacci链上进行的，但我们期望其结果可以推广到其他准周期模型中。

基金项目

本项目获得基金项目支持：国家自然科学基金资助项目No. 11674102。

NOTES

^*通讯作者Email: [e-mail]