具有扰动的非线性系统最优控制问题

An Optimal Control Problem for Nonlinear Systems with Perturbations

摘要: 在本文中，我们发展了一类具有扰动的非线性系统最优控制理论。该问题的目标是通过建立一个框架来解决最优控制问题，使得参数化的代价函数是最小的。为了避免求解哈密顿雅可比贝尔曼方程的稳态形式，我们设计了一个代价函数，它依赖于动态系统，Lyapunov函数，通过求解哈密顿雅可比贝尔曼方程获得了一个稳定的反馈控制器的具体表达式，并且该反馈控制器使得系统是渐近稳定的。最后通过一个实例来说明本文所提方法的有效性。

Abstract: In this paper, we develop a class of optimal control theory for nonlinear systems with perturbations. The objective of this problem is to establish a framework to solve the optimal control problem so that the parameterized cost function is minimized. In order to avoid solving the steady- state form of the Hamilton-Jacobi-Bellman equation, we design a cost function, which depends on the dynamic system, Lyapunov function. By solving the Hamilton-Jacobi-Behrman equation, we obtain a concrete expression of a stable feedback controller, and the feedback controller makes the system asymptotically stable. Finally, an example is given to illustrate the effectiveness of the proposed method.

1. 引言

线性系统稳定性分析是控制领域的一个重要研究方向，而外部扰动作用下系统的稳定性问题是工程领域的研究热点之一。在现实生活中，由于系统自身的原因，或者输电路故障，机器老化，发电机失负荷等都会使得系统失去稳定性，具有这些扰动因素的系统就是扰动系统。近年来，扰动系统的稳定性得到了大量的研究 [1] [2] [3] [4] [5] 。

现代工程一个重要的特点就是对某种可控的物体寻求某种控制过程，从而达到预先的目的，这就是控制。所谓最优控制问题的提出，就是将通常的最优控制问题抽象成一个数学问题，并用数学语言严格的表示出来。近年来，有关线性系统的最优控制问题引起了许多学者的关注。在自然界中，控制系统总是会受到外界扰动的影响，例如海洋系统中海浪力或者风力的扰动，飞行系统中机翼所承受风力的扰动等 [6] ，因此研究系统外部扰动作用下的最优控制问题具有一定的实际意义。近年来，关于系统的最优控制问题得到了大量的研究 [2] [6] [7] [8] 。文献 [9] 将带有逻辑判断的脉冲表达式转换为代数表达式，进而使用Mazur定理证明最优控制的存在性。文献 [10] 根据微分方程最优化问题的结论对模型进行了最优控制。文献 [6] 针对外部扰动的线性系统，提出一种前馈–反馈最优控制的逐次逼近算法。但是文献 [6] [9] [10] 都并没有给出最优控制的具体表达式。文献 [7] 利用Lyapunov稳定性判据和脉冲微分方程等理论，以一类非线性系统作为研究对象，得到了系统稳定的判据，控制对象不用每时每刻都受控制器的影响，从而极大的减少了成本。然而具有扰动的非线性系统的最优控制问题却没有得到很好的发展。

本文的目的是研究在外部扰动作用下的线性系统最优控制问题，找到最优的反馈控制降低运行成本，通过求解哈密顿雅可比贝尔曼方程的稳态形式，构造一种灵活的代价函数使得参数化的代价函数是最小的，并且得到稳定的反馈控制器，最重要的是，本文得到了反馈控制器的具体表达式，该反馈控制器使得系统是渐近稳定的，最后通过一个实例验证本文中所提方法的有效性。本文的其余部分组织如下：在第二节中介绍一些预备知识，第三节中给出了具有扰动的非线性系统的最优控制的主要结果，第四节中提供了一个实例来证明所提方法的有效性。

2. 预备知识

在本节中，介绍一些基本的符号以及一些稳定性定理。N表示所有正整数集，R表示所有实数， $R_{+}$ 表示非负实数集，用欧几里得范数 $\Vert ·\Vert$ 表示n维实空间 $R^n$ ， $R^{n\times m}$ 表示 $n\times m$ 实矩阵， $P^m$ 表示 $m\times m$ 的正定矩阵， $B_{\delta }\left(x\right)$ 表示以 $\delta$ 为中心x为半径的开球， $A^{\text{T}}$ 表示矩阵A的转置， $I_n$ 表示 $n\times n$ 单位矩阵。对于 $A,B\in R^{m\times n}$ 或着 $A,B\in R^n$ ， $A\ge B$ ( $A\le B,A>B,A<B$ )表示对应元素 $A,B$ 满足相应不等式 $\ge$ ( $\le ,>,<$ )。特别的，如果 $A\ge 0$ 称A为非负矩阵，如果 $x>0$ 称x为正定向量。

在稳定性的研究中，李亚普诺夫(Lyapunov)明确给出了两套解决稳定性的方法，即Lyapunov第一方法和Lyapunov第二方法。Lyapunov第一方法又称为间接法，是利用齐次状态方程解的特性判断系统的内部稳定性，适用于线性定常、线性时变、线性离散以及可线性化的非线性系统。经典控制理论中关于线性系统稳定性的判别都可以看作是Lyapunov判稳第一法的工程应用。Lyapunov第二方法又称为直接法，它不是求解微分方程组，而是通过构造所谓的Lyapunov函数(标量函数)来直接判断运动的稳定性，因此又称为直接法。在现代控制理论中，Lyapunov第二方法是研究稳定性的主要方法，也是研究非线性时变系统最有效的方法，是许多系统研究稳定性的有效工具。本文中需要用到的方法为Lyapunov第二方法，下面来简单介绍一下Lyapunov意义下的稳定性。

我们首先考虑一般的非线性自治动力系统

$\stackrel{\dot{}}{x}\left(t\right)=f\left(x\left(t\right)\right),x\left(0\right)=x_0,t\ge 0$ (1)

其中 $x\left(t\right)\in D\subseteq R^n$ ， $x\left(t\right)$ 为系统状态， $f:D\to R^n$ ，是连续的函数且 $f\left(0\right)=0$ ，D是开集且 $0\in D$ ，下

面的定义介绍了当 $t\ge 0$ 时稳定性的几种类型对应系统(1)的零解。

定义2.1 [11] 对于任意的 $\epsilon >0$ ，存在 $\delta =\delta \left(\epsilon \right)>0$ ，使得对任意的 $x\left(0\right)<\delta$ 有

$\Vert x\left(t\right)\Vert <\epsilon ,t\ge 0$

则称系统(1)的零解是Lyapunov稳定(见图1)。

定义2.2如果系统(1)的零解是Lyapunov稳定的且存在 $\delta >0$ ，使得对任意的 $x\left(0\right)<\delta$ 有

$\underset{t\to \infty }{\lim }x\left(t\right)=0$

则称系统(1)的零解是(局部)渐近稳定(见图2)。

定义2.3如果系统(2.1)的零解是Lyapunov稳定的且对于任意的 $x\left(0\right)\in R^n$ 有

$\underset{t\to \infty }{\lim }x\left(t\right)=0$

则称系统(1)的零解是全局渐近稳定。

定义2.4如果 $\alpha ,\beta ,\delta >0$ ，使得对于任意的 $x\left(0\right)<\delta$ 有

$\Vert x\left(t\right)\Vert \le \alpha \Vert x\left(0\right)\Vert {\text{e}}^{-\beta t},t\ge 0$

则称系统(1)的零解是(局部)指数稳定。

定义2.5 [12] 如果 $\alpha ,\beta >0$ ，使得对于任意的 $x\left(0\right)\in R^n$ 有

$\Vert x\left(t\right)\Vert \le \alpha \Vert x\left(0\right)\Vert {\text{e}}^{-\beta t},t\ge 0$

则称系统(1)的零解是全局指数稳定。

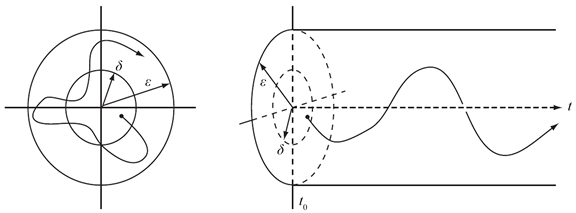
Figure 1. The equilibrium point is Lyapunov stable [12]

图1. 平衡点的Lyapunov稳定 [12]

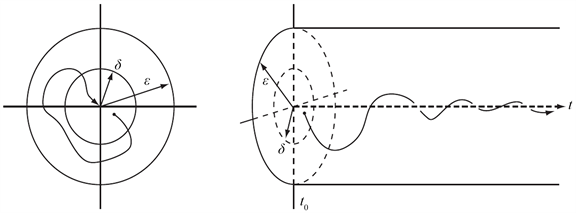
Figure 2. Asymptotic stability of the equilibrium point [12]

图2. 平衡点的渐近稳定 [12]

显然，指数稳定意味着渐近稳定，渐近稳定意味着Lyapunov稳定。下面的定理为Lyapunov第二方法，也称为Lyapunov直接法，是本文中判断系统稳定性的有效工具。令 $V:D\to R$ 是一个连续可微函数，沿系统(1)的轨迹求导，记为 $\stackrel{\dot{}}{V}\left(x\right)=V^{\prime }\left(x\right)f\left(x\right)$ ，且 $V^{\prime }\left(x\right)$ 依赖于系统(2.1)。

定理2.1 [12] 考虑非线性动态系统(1)，假设存在一个连续可微的函数 $V:D\to R$ 使得

$V\left(0\right)=0$

$V\left(x\right)>0,x\in D,x\ne 0$

$V^{\prime }\left(x\right)f\left(x\right)\le 0,x\in D$

那么系统(1)的零解是Lyapunov稳定，另外，如果

$V^{\prime }\left(x\right)f\left(x\right)<0,x\in D,x\ne 0$

那么系统(1)的零解是渐近稳定。最后，如果存在 $\alpha ,\beta ,\epsilon >0$ ， $p\ge 1$ ，使得对任意的 $V:D\to R$ 有

$\alpha {\Vert x\Vert }^p\le V\left(x\right)\le \beta {\Vert x\Vert }^p,x\in D,$

$V^{\prime }\left(x\right)f\left(x\right)\le -\epsilon V\left(x\right),x\in D,$

那么系统(1)的零解是指数稳定。

3. 扰动系统的最优控制

3.1. 系统描述

为了解决具有扰动系统的最优控制问题，考虑如下非线性系统

$\stackrel{\dot{}}{x}\left(t\right)=f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u\left(t\right)+h\left(x\left(t\right)\right)\varpi \left(t\right),x\left(0\right)=x_0,t\ge 0$ (2)

$x\left(t\right),f\left(t\right)$ 如(1)式中定义， $g:R^n\to R^{n\times m}$ ，(2)中的 $u\in R^m$ 被限制于由可测函数组成的可容许类控制， $h:R^n\to R^n$ 为光滑函数， $\varpi$ 为外部扰动。连续函数 $\varphi :R^n\to R^m$ 满足 $\varphi \left(0\right)=0$ 称为一个控制率。如果 $u\left(t\right)=\varphi \left(x\left(t\right)\right),t\ge 0$ ，其中 $\varphi (\cdot )$ 是一个控制率， $x\left(t\right)$ 满足(2)式，那么我们称 $u(\cdot )$ 是一个反馈控制率给定一个控制率 $\varphi (\cdot )$ 和一个反馈控制率 $u\left(t\right)=\varphi \left(x\left(t\right)\right)$ ，那么系统(2)有如下的形式

$x\left(t\right)=f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \left(t\right),x\left(0\right)=x_0,t\ge 0,$ (3)

定义一组调节控制器

$\mathcal{S}\left(x_0\right)=\{u(\cdot ):u(\cdot )$ 是可容许的， $x\left(t\right)$ 由系统(2)给出且满足 $\underset{t\to \infty }{\lim }x\left(t\right)=0\}$

下面引入性能积分 $L\left(x,u\right)$ 有如下形式

$L\left(x,u\right)=L_1\left(x\right)+L_2\left(x\right)+u^{\text{T}}R\left(x\right)u$ (4)

其中 $L_1:R^n\to R,L_2:R^n\to R^{1\times m},R:R^n\to P^m$ 。

3.2. 最优控制理论

下面给出本文的主要定理。

定理2.1 考虑非线性动态系统(2)且性能函数为

$J\left(x_0,u(\cdot )\right)={\displaystyle {\int }_0^{\infty }\left[L_1\left(x\left(t\right)\right)+L\left(x\left(t\right)\right)u\left(t\right)+u^{\text{T}}\left(t\right)R\left(x\left(t\right)\right)u\left(t\right)\right]\text{d}t}$ (5)

假设存在一个连续可微函数 $V:R^n\to R$ 和 $L_2:R^n\to R^{1\times m}$ 使得：

(i) $V\left(0\right)=0$ ，

(ii) $V\left(x\right)>0,x\in D,x\ne 0$ ，

(iii) $L_2\left(0\right)=0$ ，

(iv) $V\left(x\right)\to \infty$ 当 $\Vert x\Vert \to \infty$ 时，

(v) $V^{\prime }\left(x\right)\left[f\left(x\right)-\frac{1}{2}g\left(x\right)R^{-1}\left(x\right)L_2^{\text{T}}\left(x\right)-\frac{1}{2}g\left(x\right)R^{-1}\left(x\right)g^{\text{T}}\left(x\right){V^{\prime }}^{\text{T}}\left(x\right)+h\left(x\right)\varpi \right]<0,x\in R,x\ne 0$ ，

那么闭环系统(3)的零解是全局渐近稳定的，且反馈控制率为

$\varphi \left(x\right)=-\frac{1}{2}{R}^{\text{T}}\left(x\right)\left[L_2^{\text{T}}\left(x\right)+g^{\text{T}}\left(x\right){V^{\prime }}^{\text{T}}\left(x\right)\right]$ (6)

性能函数(5)与

$L_1\left(x\right)={\varphi }^{\text{T}}\left(x\right)R\left(x\right)\varphi \left(x\right)-V^{\prime }\left(x\right)\left[f\left(x\right)+h\left(x\right)\varpi \right]$ (7)

在某种意义上最小化

$J\left(x_0,\varphi \left(x(\cdot )\right)\right)=\underset{u(\cdot )\in \mathcal{S}\left(x_0\right)}{\min }J\left(x_0,u(\cdot )\right),x_0\in R$ (8)

最后，

$J\left(x_0,\varphi \left(x(\cdot )\right)\right)=V\left(x_0\right),x_0\in R^n$ (9)

证明：设Hamilton函数有如下形式：

$\begin{array}{c}H\left(x,u\right)=L\left(x,u\right)+V^{\prime }\left(x\right)\left[f\left(x\right)+g\left(x\right)u\left(x\right)+h\left(x\right)\varpi \right]\\ =L_1\left(x\right)+L_2\left(x\right)u+u^{\text{T}}R\left(x\right)u+V^{\prime }\left(x\right)\left[f\left(x\right)+g\left(x\right)u\left(x\right)+h\left(x\right)\varpi \right]\end{array}$ (10)

令 $\partial H/\partial x=0$ 可以得到反馈控制率(6)，即

$L_2^{\text{T}}\left(x\right)+2R\left(x\right)u+g^{\text{T}}\left(x\right){V^{\prime }}^{\text{T}}\left(x\right)=0$

由条件(iv)，(v)和定理2.1可以得到闭环系统(3)的零解是全局渐近稳定的。由(6)、(7)和(10)可以得到

$\begin{array}{c}H\left(x,\varphi \left(x\left(t\right)\right)\right)=L_1\left(x\left(t\right)\right)+L_2\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+{\varphi }^{\text{T}}\left(x\left(t\right)\right)R\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)\\ +V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]\\ =L_1\left(x\left(t\right)\right)-{\varphi }^{\text{T}}\left(x\left(t\right)\right)R\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]\\ =0,\end{array}$ (11)

由条件(6)、(10)和(11)可以得到

$\begin{array}{c}H\left(x,u\right)=H\left(x,u\right)-H\left(x,\varphi \right)\\ =L_2\left(x\left(t\right)\right)\left[u-\varphi \left(x\left(t\right)\right)\right]+u^{\text{T}}R\left(x\left(t\right)\right)u-{\varphi }^{\text{T}}\left(x\left(t\right)\right)R\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)\\ +V^{\prime }\left(x\left(t\right)\right)g\left(x\left(t\right)\right)\left[u-\varphi \left(x\left(t\right)\right)\right]\\ =-2\varphi \left(x\left(t\right)\right)R\left(x\left(t\right)\right)\left[u-\varphi \left(x\left(t\right)\right)\right]+u^{\text{T}}R\left(x\left(t\right)\right)u-{\varphi }^{\text{T}}\left(x\left(t\right)\right)R\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)\\ ={\left[u-\varphi \left(x\left(t\right)\right)\right]}^{\text{T}}R\left(x\left(t\right)\right)\left[u-\varphi \left(x\left(t\right)\right)\right]\\ \ge 0,t\ge 0,u\in R^m\end{array}$ (12)

令为(3)的解，那么我们有

${\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(3\right)}=V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]$ (13)

由(10)、(11)和(13)有

$\begin{array}{c}L\left(x,\varphi \left(x\left(t\right)\right)\right)=-{\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(3\right)}+L\left(x,\varphi \left(x\left(t\right)\right)\right)+V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)\varphi \left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]\\ =-{\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(3\right)}\end{array}$ (14)

把(14)式两边同时从0到t积分，可以得到

${\displaystyle {\int }_0^{t}L\left(s,\varphi \left(x\left(s\right)\right)\right)\text{d}s}=V\left(t_0\right)-V\left(t\right),t\ge 0$ (15)

令 $t\to \infty$ 可以得到

$J\left(x_0,\varphi \left(x(\cdot )\right)\right)=V\left(x_0\right),x_0\in R^n$ (16)

故(9)式得证。下面对于 $\forall t\ge 0,u\in \mathcal{S}\left(x_0\right)$ ， $x\left(t\right)$ 表示为(2)式的解，那么我们有

${\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(2\right)}=V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u\left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]$ (17)

由(10)和(11)，我们有

$\begin{array}{c}L\left(x,u\left(x\left(t\right)\right)\right)=-{\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(2\right)}+L\left(x,u\left(x\left(t\right)\right)\right)+V^{\prime }\left(x\left(t\right)\right)\left[f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u\left(x\left(t\right)\right)+h\left(x\left(t\right)\right)\varpi \right]\\ =-{\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(2\right)}+H\left(x,u\left(t\right)\right)\end{array}$ (18)

类似于(15) (16)的讨论，由(12)和(18)以及 $u(\cdot )\in \mathcal{S}\left(x_0\right)$ 得到

$\begin{array}{c}J\left(x_0,\varphi \left(x(\cdot )\right)\right)={\displaystyle {\int }_0^{\infty }\left[-{\stackrel{\dot{}}{V}\left(x\left(t\right)\right)|}_{\left(2\right)}+H\left(x,u\left(t\right)\right)\right]\text{d}t}\\ =V\left(t_0\right)-V\left(t\right)+{\displaystyle {\int }_0^{\infty }H\left(x,u\left(t\right)\right)\text{d}t}\\ \ge V\left(t_0\right)=J(t_0,u(\; \cdot \; ))\end{array}$

这就证明了(8)式，证明完成。

4. 实例分析

例1考虑下面非线性方程

$\begin{array}{l}{\stackrel{\dot{}}{x}}_1\left(t\right)=x_2^4\left(t\right)-x_1^3\left(t\right)\\ {\stackrel{\dot{}}{x}}_2\left(t\right)=x_1^2\left(t\right)+u\left(t\right)\end{array}$ (19)

选择一个Lyapunov函数为 $V\left(x\right)=p_1{x}_1^2+p_2{x}_2^2$ 其中 $x\triangleq {\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]}^{\text{T}},p_1>0,p_2>0$ 性能积分为 $L\left(x,u\right)=L_1\left(x\right)+L_2\left(x\right)u+u^{\text{T}}R\left(x\right)u$ 其中 $R\left(x\right)>0$ 和性能函数(5)，设 $L_2\left(x\right)=2R\left(\frac{p_1}{p_2}{x}_1{x}_2^3+x_1^2\right)$ 满足条件(v)，由(6)可得反馈控制率为

$\begin{array}{c}u=\varphi \left(x\right)=-\frac{1}{2}{R}^{-1}\left(x\right)\left\{\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}2p_1{x}_1\\ 2p_2{x}_2\end{array}\right]+2R\left(\frac{p_1}{p_2}{x}_1{x}_2^3+x_1^2\right)\right\}\\ =-R^{-1}{p}_2{x}_2-\frac{p_1}{p_2}{x}_1{x}_2^3-x_1^2\end{array}$ (20)

且性能函数(5)有

$L_1\left(x\right)=R\left(x\right){\left[R^{-1}{p}_2{x}_2+\frac{p_1}{p_2}{x}_1{x}_2^3+x_1^2\right]}^2-\left[2p_1{x}_1\left(x_2^4-x_1^3\right)+2p_2{x}_2{x}_1^2\right]$ (21)

而且 $V\left(x\right)$ 满足条件(iv)

$\begin{array}{c}\stackrel{\dot{}}{V}\left(x\right)=2p_1{x}_1{x}_2^4-2p_1{x}_1^4+2p_2{x}_1^2{x}_2-2p_2{x}_2\left(\frac{p_1}{p_1}{x}_1{x}_2^3+x_1^2\right)-p_2{x}_2{R}^{-1}2p_2{x}_2\\ =2p_1{x}_1{x}_2^4-2p_1{x}_1^4+2p_2{x}_1^2{x}_2-2p_1{x}_1{x}_2^4-2p_2{x}_1^2{x}_2-2\frac{p_2^2}{R}{x}_2^2\\ =-2p_1{x}_1^4-2\frac{p_2^2}{R}{x}_2^2<0\end{array}$

故定理1条件满足。该系统在控制率(20)作用下的运动轨迹如图3所示。

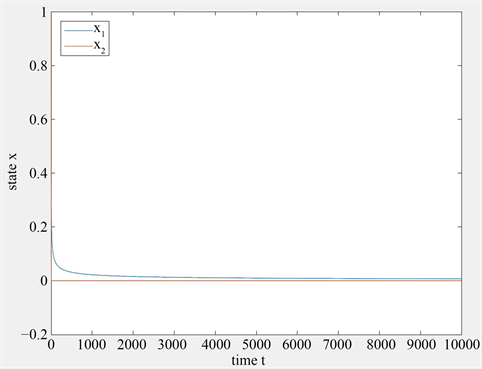
Figure 3. Motion trajectory of system (19) under feedback control rate (20)

图3. 在反馈控制率(20)下系统(19)的运动轨迹

5. 结论

本文研究了一类具有扰动的非线性系统的最优控制问题。 [12] 中只考虑了非线性系统的最优控制问题，由于现实生活中扰动的存在，本文考虑了一类具有扰动系统的最优控制，是对 [12] 中结果的进一步改进。通过构造灵活的代价函数，避免哈密顿雅可比贝尔曼方程求解的复杂性，并且得到了反馈控制器的具体表达式，该反馈控制器使得系统是渐近稳定的且在某种意义上代价函数最小，因此具有一定的应用价值。一个最后通过一个实例和仿真验证了本文中所提方法的有效性。目前还没有关于具有扰动的非线性系统的最优控制问题，因此本文提出的最优控制理论进一步地完善了具有扰动的非线性系统的最优控制问题。然而本文的研究结果只是初步的，对于具有扰动的时滞非线性系统，如何找到最优控制器，使得非线性–非二次代价函数最小是个有趣的问题，还有待进一步研究。