基于变分贝叶斯隐马尔科夫模型的股票价格指数预测

Prediction of Stock Price Index Based on Variational Bayesian Hidden Markov Model

摘要: 本文将传统的隐马尔科夫模型中用于参数学习的Baum-Welch算法改进为变分贝叶斯算法，并将变分贝叶斯隐马尔科夫模型应用于股票价格指数预测，分别选取国外市场美股S&P500指数以及国内市场沪深300指数进行预测，并与传统的隐马尔科夫模型、BP神经网络、ARIMA模型相比较，得出结论变分贝叶斯隐马尔科夫模型对于大规模数据处理更有优势，运算速度快且预测精度更高。

Abstract: In this paper, the Baum-Welch algorithm used for parameter learning in the traditional Hidden Markov Model is improved to the variational Bayes algorithm, and the variational Bayes Hidden Markov model is applied to the stock price index prediction. The S&P500 index of the United States stock in foreign markets and the HuShen300 index of the domestic market are selected for predic-tion. Compared with the traditional Hidden Markov Model, BP neural network and ARIMA model, it is concluded that the variational Bayes Hidden Markov Model has more advantages for large- scale data processing, and the operation speed is more faster and the prediction accuracy is higher.

1. 引言

股票价格指数是证券交易所或金融机构编制出的，可以反映整个股票市场上的各支股票价格的总体水平及变动情况的指标，它能灵敏反应一个国家或地区政治、经济的发展状态。因此，预测股票价格指数对投资者进行投资理财，判断当前经济形势具有重要意义。

对股票的价格指数预测可以采用多种方法，例如ARIMA、BP神经网络、SVM方法，相比之下，隐马尔科夫模型(Hidden Markov Models, HMM)的优点更多的在于其坚实的理论基础，既往的学者也探究过马尔科夫模型、隐马尔科夫模型以及改良后的隐马尔科夫模型在金融领域的应用，例如Hassan和Nath在2005、2007的两篇文章中应用HMM来预测股票价格 [1] [2] ；朱嘉瑜、叶海燕、高鹰结合人工神经网络技术与PSO算法，得到APHMM组合模型 [3] ；兰锦池用Gibbs抽样的MCMC方法获得Bayes隐马尔科夫模型的后验估计进而刻画人民币汇率的动态变化规律 [4] ；汪金菊建立HMM-ARMA-GARCH模型度量金融市场风险 [5]。可以看出，目前不少学者已经运用HMM以及改进的HMM模型来进行股票预测，本文也想从改进的角度，提出更加优化的模型。

本文的创新之处在于从隐马尔科夫模型算法本身进行改进，将原有的求解模型参数学习问题的Baum-Welch算法转变成变分贝叶斯算法(Variational Bayesian, VB)，以往的很多研究已经表明VB相比其他方法采样更快，适合大规模数据，需要快速训练模型的场景。因此本文将VB与HMM结合建立变分贝叶斯隐马尔科夫模型(以下简称VBHMM)，探讨组合模型进行股票价格指数预测的可行性。

2. 隐马尔科夫模型的理论基础

2.1. 马尔科夫链

隐马尔科夫模型是在马尔科夫链的基础上延伸而来，它有两个部分组成即马尔科夫链与一般随机过程 [6]。

设 $\left\{X_t,t\in T\right\}$ 为一随机过程，对任意的t以及状态 $x_0,x_1,\cdots ,x_n$ ，有下面的式子成立

$P\left\{X_{t+1}=x_{t+1}|X_0=x_0,X_1=x_1,\cdots ,X_n=x_n\right\}=P\left\{X_{t+1}=x_{t+1}|X_n=x_n\right\}$

即某一个时刻t的状态只依赖于前一个时刻 $t-1$ 的状态，也称为马尔科夫链的无记忆性 [7]。

2.2. 隐马尔科夫模型相关定义

隐马尔科夫模型顾名思义，它的状态不能直接观察到，隐马尔科夫模型中包含两种状态类型可观测状态和隐状态，两者之间并没有一一对应关系，所以称为“隐”马尔科夫模型，如图1所示。

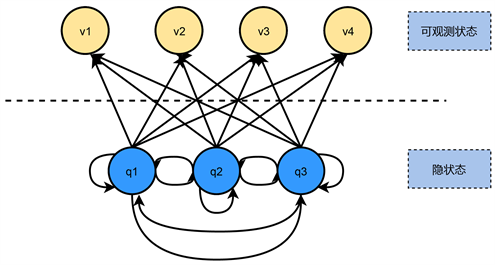
Figure 1. Diagram of Hidden Markov Models

图1. 隐马尔科夫模型图示

记隐状态集合为 $Q=\left\{q_1,q_2,\cdots ,q_K\right\}$ ，可观测状态集合为 $V=\left\{v_1,v_2,\cdots ,v_M\right\}$ ，隐状态序列为 $Z=\left\{z_1,z_2,\cdots ,z_T\right\}$ ，观测态序列为 $X=\left\{x_1,x_2,\cdots ,x_T\right\}$ ，需要注意的是这里的K与M不一定相等。

HMM模型记为 $\Lambda =\left(A,B,\Pi \right)$ ，详解如下：

1) $A={\left[a_{ij}\right]}_{K\times M}$ ， $a_{ij}=P\left(z_{t+1}=q_j|z_t=q_i\right)$ ，A称为状态转移矩阵；

2) $B={\left[b_j\left(m\right)\right]}_{K\times M}$ ， $b_j\left(m\right)=P\left(x_t=v_m|z_t=q_j\right)$ ，B称为观测状态生成矩阵；

3) $\Pi ={\left[\pi \left(z\right)\right]}_K$ ， $\pi \left(z\right)=P\left(z_1=q_i\right)$ ， $\Pi$ 为隐状态初始概率分布。

如表1所示为HMM模型各参数的含义。

Table 1. Meaning of model parameters

表1. 模型参数含义

2.3. 关于隐马尔科夫模型的3个经典问题

1) 识别问题。已知观测序列 $X=\left\{x_1,x_2,\cdots ,x_T\right\}$ 和模型参数 $\Lambda =\left(A,B,\Pi \right)$ ，计算观测序列出现的概率 $P\left(X|\Lambda \right)$ ，通常采用前向-后向算法来求解此问题；

2) 模型参数学习问题。即给定观测序列 $X=\left\{x_1,x_2,\cdots ,x_T\right\}$ ，求出模型的各个参数 $\Lambda =\left(A,B,\Pi \right)$ ，最经典做法的是采用基于EM (Expectation Maximization)算法的Baum-Welch算法求解；

3) 解码问题。已知观测序列 $X=\left\{x_1,x_2,\cdots ,x_T\right\}$ 和模型参数 $\Lambda =\left(A,B,\Pi \right)$ ，要求使得 $P\left(Z|X\right)$ 最大时的隐状态序列 $Z=\left\{z_1,z_2,\cdots ,z_T\right\}$ ，通常使用Viterbi算法求解。

3. 变分贝叶斯方法原理

变分贝叶斯即变分推断，类属于贝叶斯近似推断方法，它的特点是将后验推断问题转化为优化问题进而求解，相比于以往学者用到的马尔科夫链蒙特卡罗方法(Markov Chain Monte Carlo, MCMC)，VB更适合大规模数据近似推断问题的求解 [8] [9]。

设 $X=\left\{x_1,x_2,\cdots ,x_T\right\}$ 是观测变量， $\theta =\left\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_p\right\}$ 是模型参数，根据贝叶斯定理有

$p\left(\theta |x\right)=\frac{p\left(x,\theta \right)}{p\left(x\right)}=\frac{p\left(x|\theta \right)p\left(\theta \right)}{p(\; x\; )}$

其中， $p\left(\theta |x\right)$ 即为所求的后验分布， $p\left(\theta \right)$ 是参数的先验信息， $p\left(x|\theta \right)$ 是似然函数， $p\left(x\right)$ 可以写为如下边际分布的形式：

$p\left(x\right)={\displaystyle {\int }_{\theta }p\left(x,\theta \right)\text{d}\theta }={\displaystyle {\int }_{\theta }p\left(x\text{|}\theta \right)p\left(\theta \right)\text{d}\theta }$

VB将求解 $p\left(\theta |x\right)$ 的问题转化为在Q中找到距离 $p\left(\theta |x\right)$ 最近的点 $q^{*}$ ，这里的距离用KL距离(Kullback-Libler Divergence)来定义，即

$\begin{array}{c}{q}^{*}\left(\theta \right)=\underset{q\left(\theta \right)\in Q}{\arg }\min \text{KL}\left(q\left(\theta \right)\left|\right|p\left(\theta |x\right)\right)\\ =\underset{q\left(\theta \right)\in Q}{\arg }\min {\displaystyle {\int }_{\theta }q\left(\theta \right)\log \left[\frac{q\left(\theta \right)}{p\left(\theta |x\right)}\right]\text{d}\theta }\end{array}$

又因为 $p\left(x\right)$ 是只与确定的观测变量有关，所以在计算中可以认定为常数，有

$\begin{array}{c}\log p\left(x\right)=E_q\left[\log p\left(x\right)\right]\\ ={\displaystyle {\int }_{\theta }q\left(\theta \right)}\log p\left(x\right)\text{d}\theta \\ ={\displaystyle {\int }_{\theta }q\left(\theta \right)}\log \frac{p\left(x,\theta \right)}{p\left(\theta |x\right)}\text{d}\theta \\ ={\displaystyle {\int }_{\theta }q\left(\theta \right)}\log \frac{p\left(x,\theta \right)q\left(\theta \right)}{p\left(\theta |x\right)q\left(\theta \right)}\text{d}\theta \\ ={\displaystyle {\int }_{\theta }q\left(\theta \right)}\log \frac{p\left(x,\theta \right)}{q\left(\theta \right)}\text{d}\theta +{\displaystyle {\int }_{\theta }q\left(\theta \right)}\log \frac{q\left(\theta \right)}{p\left(\theta |x\right)}\text{d}\theta \\ =\text{ELBO}+\text{KL}\left(q\left(\theta \right)\left|\right|p\left(\theta |x\right)\right)\end{array}$

这里的ELBO (Evidence Lower Bound)可以由Jensen不等式推导得出，过程如下：

$\begin{array}{c}\log p\left(x\right)=\log {\displaystyle {\int }_{\theta }p\left(x,\theta \right)\text{d}\theta }\\ =\log {\displaystyle {\int }_{\theta }q\left(\theta \right)\frac{p\left(x,\theta \right)}{q\left(\theta \right)}\text{d}\theta }\\ \ge {\displaystyle {\int }_{\theta }q\left(\theta \right)\log \frac{p\left(x,\theta \right)}{q\left(\theta \right)}\text{d}\theta }=\text{ELBO}\end{array}$

又因为 $KL\ge 0$ ，则优化问题进一步转化为

$\begin{array}{c}{q}^{*}\left(\theta \right)=\underset{q\left(\theta \right)\in Q}{\arg }\min \text{KL}\left(q\left(\theta \right)\left|\right|p\left(\theta |x\right)\right)\\ =\underset{q\left(\theta \right)\in Q}{\arg }\max \text{ELBO}(\; q\; )\end{array}$

再根据Mean Field理论

$q\left(\theta \right)={\displaystyle \underset{i=1}{\overset{p}{\prod }}{q}_i}(\; \theta \; i\; )$

将 $\theta$ 分为两部分 ${\theta }_j$ 与除 ${\theta }_j$ 以外的部分 ${\theta }_{-j}$ 对ELBO进行积分，可以得到

$\begin{array}{c}\text{ELBO}\left[q_j\left({\theta }_j\right)\right]={\displaystyle {\int }_{\theta }q\left(\theta \right)\log \frac{p\left(x,\theta \right)}{q\left(\theta \right)}\text{d}\theta }\\ =E_q\left[\log p\left(x,\theta \right)\right]-E_q\left[\log q\left(\theta \right)\right]\\ ={\displaystyle {\int }_{{\theta }_j}{q}_j}\left({\theta }_j\right)E_{q_{-j}}\left[\log p\left(x,\theta \right)\right]\text{d}{\theta }_j-E_{q_j}\left[\log q_j\left(\theta \right)\right]+\text{const}\end{array}$

这里要使ELBO最大，则

$\begin{array}{l}\log q_j^{*}\left({\theta }_j\right)=E_{q_{-j}}\left[\log p\left(x,\theta \right)\right]+\text{const}\\ q_j^{*}\left({\theta }_j\right)\propto \exp \left\{E_{q_{-j}}\left[\log p\left(x,\theta \right)\right]\right\}\end{array}$

经过标准化求出const的值，最终得到表达式

$q_j^{*}\left({\theta }_j\right)=\frac{\exp \left\{E_{q_{-j}}\left[\log p\left(x,\theta \right)\right]\right\}}{{\displaystyle {\int }_{z_j}\exp \left\{E_{q_{-j}}\left[\log p\left(x,\theta \right)\right]\right\}\text{d}{\theta }_j}}$

利用坐标上升法迭代求解。

4. VBHMM理论

4.1. 共轭先验分布的设定

本文使用变分贝叶斯算法来求解隐马尔科夫模型的参数，基于上文的VB理论结合HMM推导如下：

首先需要假定模型参数的先验分布，易证狄利克雷分布是状态转移矩阵A的共轭先验分布，因此，对于任意一个隐状态 $q_i$ ，对其每一个转移概率 $\left\{a_{ij}|j=1,\cdots ,K\right\}$ 都给定一个独立的狄利克雷先验分布，

$p\left(A\right)={\displaystyle \underset{i}{\prod }Dir\left(a_i|\left\{{\alpha }_{ij}^{\left(0\right)}\right\}\right)},$

$\left\{{\alpha }_{ij}^{\left(0\right)}\right\}$ 为超参数的初始化。由于金融时间序列一般情况下都不是标准的高斯分布，这里使用多元混合高斯分布，即每一个观测概率都是一个一元高斯分布，而不同的取值则对应不同的高斯分布，设 $\left\{{\varphi }_k\right\}$ 表示第k个观测状态的概率密度函数的参数集合，有

$\begin{array}{c}{p}_k\left(x_t|{\varphi }_k\right)=N\left(x_t|{\mu }_k,{\tau }_k^{-1}\right)\\ ={\left(\frac{{\tau }_k}{2\pi }\right)}^{T/2}\exp \left\{-\frac{{\tau }_k}{2}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left(x_t-{\mu }_k\right)}^2}\right\},\end{array}$

给定 $\mu$ 和 $\tau$ 的共轭先验分布，其中 $\mu$ 在 $\tau$ 下的条件分布是一个高斯分布， $\tau$ 来自一个伽玛分布。这是一个强假设，但这样假设的优势在于最终得到的后验分布也是一个高斯分布，式中 $\left\{m_k^{\left(0\right)},{\lambda }_k^{\left(0\right)},u_k^{\left(0\right)},v_k^{\left(0\right)}\right\}$ 是初始化的超参数，有

$\begin{array}{l}p\left(\mu |\tau \right)={\displaystyle \underset{k=1}{\overset{K}{\prod }}N\left({\mu }_k|m_k^{\left(0\right)},{\left({\lambda }_0^{\left(0\right)}{\tau }_k\right)}^{-1}\right)}\\ p\left(\tau \right)={\displaystyle \underset{k=1}{\overset{K}{\prod }}Gam\left({\tau }_k|u_k^{\left(0\right)},v_k^{\left(0\right)}\right)}.\end{array}$

4.2. 变分后验分布的计算

根据变分贝叶斯算法，给出模型参数的后验分布：

$\begin{array}{l}{q}_i\left(a_i\right)=Dir\left(a_i|\left\{{\alpha }_{ij}\right\}\right)\\ q\left({\mu }_k|{\tau }_k\right)=N\left({\mu }_k|m_k,{\left({\lambda }_k{\tau }_k\right)}^{-1}\right)\\ q\left({\tau }_k\right)=Gam\left({\tau }_k|u_k,v_k\right)\end{array}$

其中迭代之后的超参数计算如下，

$\begin{array}{l}{\alpha }_{ij}={\alpha }_{ij}^{\left(0\right)}+{\displaystyle \underset{t=1}{\overset{T-1}{\sum }}{q}_z}\left(z_1=i,z_{i+1}=j\right),\\ m_k=\left[{\lambda }_k^{\left(0\right)}{m}_k^{\left(0\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{q}_z\left(z_t=k\right)x_t}\right]{\lambda }_k^{-1},\\ {\lambda }_k={\lambda }_k^{\left(0\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{q}_z\left(z_t=k\right)},\\ u_k=u_k^{\left(0\right)}+\frac{1}{2}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{q}_z\left(z_t=k\right)},\\ v_k=v_k^{\left(0\right)}+\frac{1}{2}\left[{\displaystyle \underset{t=1}{\overset{T}{\sum }}{q}_z\left(z_t=k\right)x_t^2}+{\lambda }_k^{\left(0\right)}{m}_k^{\left(0\right)}{}^2-{\lambda }_k{m}_k^2\right].\end{array}$

那么 $q_z\left(z\right)$ 的变分后验分布就可以写为：

$\begin{array}{c}{q}_z\left(z\right)\propto {\displaystyle \underset{t=1}{\overset{T}{\prod }}{\displaystyle \underset{k=1}{\overset{K}{\prod }}{\left[\exp \left(E_q\left(\log p_k\left(x_t|{\varphi }_k\right)\right)\right)\right]}^{z_{tk}}}}{\displaystyle \underset{t=1}{\overset{T}{\prod }}{\displaystyle \underset{i=1}{\overset{K}{\prod }}{\displaystyle \underset{j=1}{\overset{K}{\prod }}\exp {\left[\left(E_q\left(\log a_{ij}\right)\right)\right]}^{z_{ti}{z}_{t+1j}}}}}\\ ={\displaystyle \underset{t=1}{\overset{T}{\prod }}{\displaystyle \underset{k=1}{\overset{K}{\prod }}{\left[\exp \frac{1}{2}\left(\Gamma \left(u_k\right)-\log v_k-\frac{u_k}{v_k}{\left(x_t-m_k\right)}^2-{\lambda }_k^{-1}\right)\right]}^{z_{tk}}}}\cdot \\ {\displaystyle \underset{t=1}{\overset{T}{\prod }}{\displaystyle \underset{i=1}{\overset{K}{\prod }}{\displaystyle \underset{j=1}{\overset{K}{\prod }}{\left[\exp \left(\Gamma \left({\alpha }_{ij}\right)-\Gamma \left({\displaystyle \underset{k=1}{\overset{K}{\sum }}{\alpha }_{ik}}\right)\right)\right]}^{z_{ti}{z}_{t+1j}}}}}\end{array}$

这里的 $\Gamma$ 为伽玛函数，其中，

$z_{tk}=\{\begin{array}{cc}1,& z_t=k\\ 0,& z_t\ne k\end{array}$

由此可以推导出变分贝叶斯算法中参数的重估公式如下，其中 $a_{ij}^{*}$ 为状态转移概率的估计， $b_{ij}^{*}$ 为观测概率的估计，

$\begin{array}{l}{a}_{ij}^{*}=\exp \left(\Gamma \left({\alpha }_{ij}\right)-\Gamma \left({\displaystyle \underset{k=1}{\overset{K}{\sum }}{\alpha }_{ik}}\right)\right)\\ b_{ij}^{*}=\exp \frac{1}{2}\left(\Gamma \left(u_k\right)-\log v_k-\frac{u_k}{v_k}{\left(x_t-m_k\right)}^2-{\lambda }_k^{-1}\right).\end{array}$

5. 实证研究

5.1. 数据选取与描述

为了综合评估VBHMM模型的预测性能，本次研究选取国外市场美股S&P500指数以及国内市场沪深300指数进行预测分析，选取其中的开盘价、最高价、最低价、收盘价为研究数据。利用训练集进行VBHMM模型的参数估计，考虑到收盘价在股票预测中更为重要，这里我们只对两只股指的收盘价进行预测。

鉴于VBHMM对于大规模数据处理起来更快、更简单，本次研究样本容量与以往研究相比更加庞大。对于S&P500指数选取2009年3月2日到2022年6月7日中交易日的数据，其中从2009年3月2日到2021年1月22日共3000个数据作为训练集，从2021年4月1日到2022年6月7日300个数据作为测试集。如图2所示为S&P500指数2009年3月2日到2022年6月7日变化曲线。图中横坐标代表年份，纵坐标代表股票价格指数。

对于沪深300指数选取2008年9月1日到2022年5月25日中交易日的数据，其中从2008年9月1日到2020年12月31日共3000个数据作为训练集，从2021年3月1日到2022年5月25日300个数据作为测试集。如图3所示为沪深300指数2008年9月1日到2022年5月25日变化曲线。图中横坐标代表年份，纵坐标代表股票价格指数。

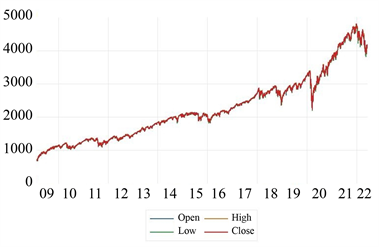
Figure 2. Change curve of S&P500 index from March 2, 2009 to June 7, 2022

图2. S&P500指数2009年3月2日到2022年6月7日变化曲线

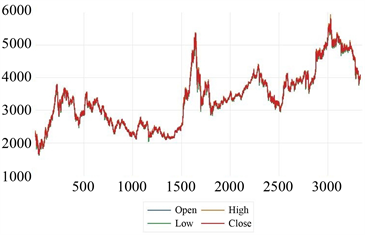
Figure 3. Change curve of HuShen300 Index from September 1, 2008 to May 25, 2022

图3. 沪深300指数2008年9月1日到2022年5月25日变化曲线

5.2. 股票价格预测

本文选取平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)来检验VBHMM模型预测精度，n为测试集的样本数， $x_d$ 为真实值， $x_d^{\text{*}}$ 为预测值，公式为：

$\text{MAPE}=\frac{1}{n}{\displaystyle \underset{d=1}{\overset{n}{\sum }}\left|\frac{x_d^{*}-x_d}{x_d}\right|}\times 100\text{\%}$ .

对S&P500指数以及沪深300指数进行d日加权预测结果如下 [10] ：

Table 2. MAPE value of d-day weighted forecast (%)

表2. d日加权预测的MAPE值(%)

表2为d日加权预测的MAPE值，横向来看单日预测结果波动较大，随着加权天数增加MAPE值越来越小，20日与30日结果相差较小，综合考虑模型复杂度，选择20日加权更适合模型预测。纵向来看VBHMM模型对于美股S&P500指数的预测结果优于沪深300指数，考虑到国内市场受政策影响较大，结果具有一定的现实意义。

图4为20日加权的S&P500指数预测图，图5为20日加权的沪深300指数预测图，图中蓝色为实际值，红色为预测值，横坐标代表天数，纵坐标代表股票价格指数。从图中也可以看出两条曲线高度吻合，预测结果较好。

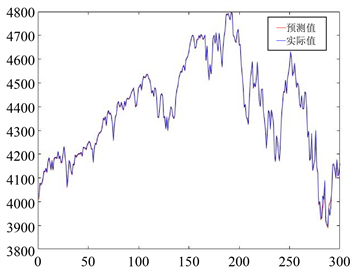
Figure 4. 20-day weighted forecast chart for the S&P500 index

图4. S&P500指数20日加权预测图

Figure 5. 20-day weighted forecast chart of HuShen300 index

图5. 沪深300指数20日加权预测图

5.3. 不同模型预测结果比较

从理论上来看，VBHMM模型与HMM模型相比较在求解模型参数问题上使用方法不同，传统的HMM模型采用Baum-Welch算法，是依托极大似然估计来求解，而VBHMM则是利用变分推断原理转化为优化问题求解。变分推断的优势就在于其对样本量较大的问题处理速度更快，因此近年来被广泛应用于机械工程以及脑科学领域 [11]，本文也是对VBHMM模型应用于股票价格预测上的一次尝试。

因此为进一步探究VBHMM模型的预测性能，比较VBHMM模型与HMM模型相比在处理大规模数据上的精度，我们又对S&P500指数以及沪深300指数利用HMM模型、BP神经网络模型、ARIMA模型分别进行预测，对S&P500指数的预测结果如图6~8所示，对沪深300指数的预测结果如图9~11所示，图中蓝色为实际值，红色为预测值，横坐标代表天数，纵坐标代表股票价格指数。

Figure 6. 20-day weighted prediction plot of the HMM for the S&P500 index

图6. HMM模型对S&P500指数的20日加权预测图

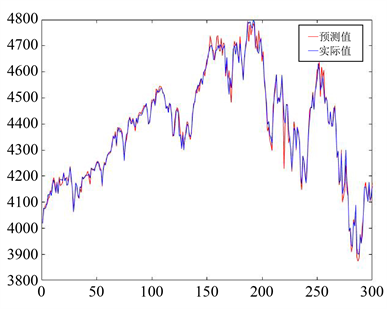
Figure 7. Prediction plot of BP neural network for S&P500 index

图7. BP神经网络对S&P500指数预测图

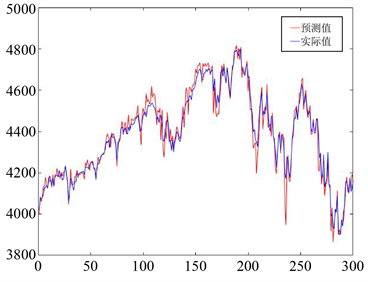
Figure 8. Prediction plot of ARIMA model for S&P500 index

图8. ARIMA模型对S&P500指数预测图

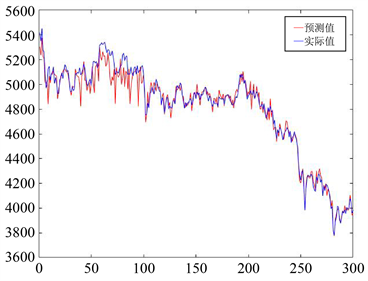
Figure 9. 20-day weighted prediction plot of the HMM for the HuShen300 index

图9. HMM模型对沪深300指数的20日加权预测图

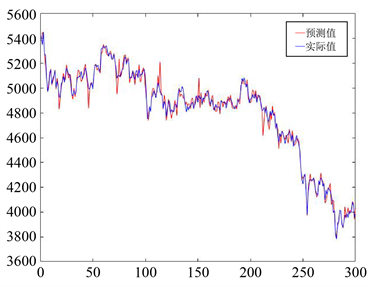
Figure 10. Prediction chart of the HuShen300 index by BP neural network

图10. BP神经网络对沪深300指数预测图

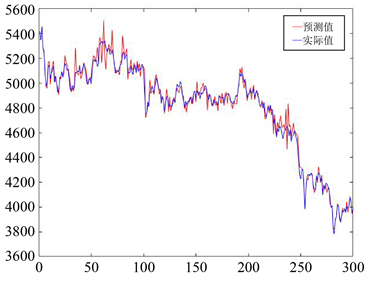
Figure 11. Prediction chart of the HuShen300 index by ARIMA model

图11. ARIMA模型对沪深300指数预测图

从上图中可以看出，对于S&P500指数和沪深300指数的预测，HMM模型、BP神经网络模型、ARIMA模型的预测结果虽然总体走势一致，然而个别天数预测值与实际值有一定程度的差异，模型表现逊色于VBHMM模型。为了更加直观地比较各模型间预测精度的差异，计算各自的MAPE值如表3所示：

Table 3. Comparison of MAPE prediction accuracy of different models (%)

表3. 不同模型的MAPE预测精度对比(%)

从表中可以看出，在四类模型中，VBHMM模型预测精度最高，其次是20日加权计算的传统的HMM模型，BP神经网络模型相比之下误差较大，ARIMA模型表现最差。可能原因在于，ARIMA模型是单变量输入单变量输出的时间序列预测模型，因此在实际操作中是用收盘价来预测收盘价，相比其他三个模型用四个价格来预测收盘价，造成结果误差较大。但由于ARIMA模型是非常经典的时间序列预测模型，因此本文把它作为对比模型共同比较也能使结论更加具有代表性。另外从结果中也可以看出，同样是20日加权的情况下，VBHMM与HMM相比对于大样本量的预测精度有较大提高，预测结果更加准确。

6. 结论与展望

本文对HMM模型的相关理论进行了总结与分析，然后引入变分贝叶斯方法，替换传统的Baum-Welch算法来进行HMM模型的参数估计。并将改进算法用于股票价格指数的预测，分别选取美股S&P500指数和沪深300指数两只股指进行预测，最后将VBHMM模型的预测结果与HMM模型、BP神经网络模型、ARIMA模型的MAPE预测精度相比较，得出结论VBHMM模型相较于传统的HMM模型以及其他模型预测精度更高、处理速度更快，体现了VBHMM模型对大规模股票数据预测的优越性。

对于股票价格预测，除了需要参照每日的价格变动情况，还应综合考虑国家政策调整、国内外经济环境、股民情绪等外部因素 [12]，本文研究只考虑了股票价格，没有综合考虑其他经济和非经济因素，这也是在之后的研究中亟待解决的问题。

NOTES

^*通讯作者。